Casing/Tubing design manual october 2005 Chevron

Подождите немного. Документ загружается.

• A trial-and-error solution is, therefore, necessary because the depth to which

the 43.16-kg/m (29-ppf) N-80 is run is balanced with the tension due to

casing suspended below. This procedure is illustrated graphically in Figure

9-3. The point at which the collapse resistance of the tube just equals the

design collapse differential pressure is 2,749 m (9,020 ft).

• This trial-and-error procedure, particularly when combined with the API

procedure for adjusting collapse resistance for axial load, can be extremely

time consuming and is best performed with computer software.

6000

6500

7000

7500

8000

8500

9000

9500

0.75 1 1.25 1.5

Collapse Load/Collapse Resistance

TVD

Figure 9-3. Illustration of Trial-and-Error Solution for Crossover in a Collapse

Design

We now have a depth at which we may cross over from the 47.62 kg/m (32 ppf)

N-80 to the less expensive 43.16 kg/m (29 ppf) N-80. Repeating the procedure,

we now ask at what depth we may abandon the 43.16 kg/m (29 ppf) N-80 for a

less expensive weight/grade combination, in this case it is 38.69 kg/m (26 ppf) N-

80. This procedure proceeds uphole until the entire wellbore has been traversed.

The results are summarized in Figure 9-2.

One complication to the procedure outlined above occurs in this example. Notice

that in determining the cross over from 43.16 kg/m (29 ppf) N-80 to 38.69 kg/m

(26 ppf) K-55 we encounter the cement top, which results in a step increase in

the design collapse differential pressure. There is a short interval near the

cement top where the axial load adjusted collapse resistance of the 38.69 kg/m

(26 ppf) N-80 is inadequate (see the curve in Figure 9-2 labeled “First Pass”). To

remedy this deficiency, we must run 43.16 kg/m (29 ppf) N-80 to a point slightly

above the cement top. This point is determined in a manner identical to that

described above, the only adjustment being to use the 1.0 design factor for

determining the design differential pressure when considering the cross over

from 43.16 kg/m (29 ppf) N-80 to 38.69 kg/m (26 ppf) N-80.

Casing/Tubing Design Manual 9-23

October 2005

We now have, within the limits of our design constraints and available inventory,

the least expensive combination of weights and grades that will perform

adequately in collapse. It now remains to check other load conditions.

9.5.1.2 Burst Design

The design for internal pressure differential takes the collapse design as its

starting point. Starting with the collapse design string, a check of each section

against the design internal pressure differential is performed and, where

appropriate, amendments to the design string are made.

The preliminary design for internal pressure is less complicated than that for

external pressure as tension enhances burst resistance and may, therefore, in

the name of conservatism be ignored.

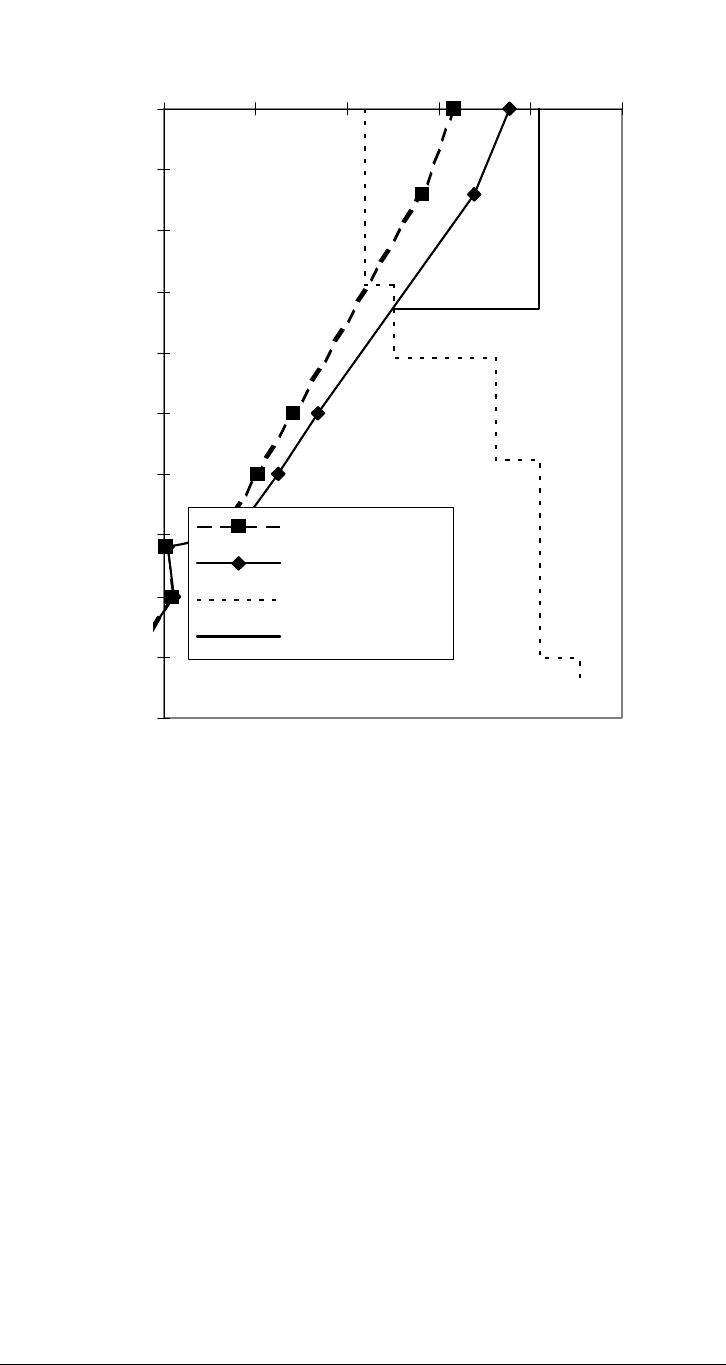
Figure 9-4 summarizes the burst design procedure. Plotting design internal

differential pressure versus depth involves two steps:

1. Given the appropriate load case, compute the appropriate internal and

external pressure profiles. For production casing, the basic load case is a

surface tubing leak. From the pore pressure distribution, the reservoir

pressure is based on a 1,761-kg/m

(14.7-ppg) gradient. Subtracting a

gas gradient of 2.26 kPa/m (0.1 psi/ft), the resulting surface pressure is

43.47 MPa (6,305 psi). The external pressure is set to the pore pressure

gradient.

2. Apply the design factor for this load case to the difference of the internal

and external pressure profiles to arrive at a design internal differential

pressure. In this particular design, the burst design factor is the Chevron

default of 1.2.

9-24 Casing/Tubing Design Manual

October 2005

1000

2000

3000

4000

5000

6000

7000

8000

9000

10000

0 2000 4000 6000 8000 10000

Differential Pressure (psi)

TVD (ft)

Differential Load

Load w/DF

Collapse Design

Burst Design

29,N

26,N

26,K

23,K

32,N

29,N

Figure 9-4. Burst Design for Production Casing Example

As seen in Figure 9-4, the burst design check suggests a large portion of the

38.69-kg/m (26-ppf) K-55 and all of the 34.23-kg/m (23-ppf) K-55 must be

replaced.

In each case we replace the inadequate tube with a weight/grade combination

that has:

• A higher burst resistance

• At least as high a collapse resistance.

For both of these tubes the replacement is 43.16-kg/m (29-ppf) N-80.

Casing/Tubing Design Manual 9-25

October 2005

We now have, within the limits of our design constraints and available inventory,

the least expensive combination of weights and grades that will perform

adequately in both collapse and burst. The design string as this point is shown in

Table 9-12.

Table 9-12. Production Casing Following Burst Design

Weight kg/m(lb/ft) Grade Interval m (ft) Length m (ft)

43.16

(29)

N-80 0-1,006

(0-3,300)

1,006

(3,300)

38.69

(26)

K-55 1,006-1,241

(3,300-4,070)

235

(770)

38.69

(26)

N-80 1,241-1,756

(4,070-5,760)

515

(1,690)

43.16

(29)

N-80 1,756-2,749

(5,760-9,020)

994

(3,260)

47.62

(32)

N-80 2,749-2,896

(9,020-9,500)

146

(480)

9.5.1.3 Axial Load Design

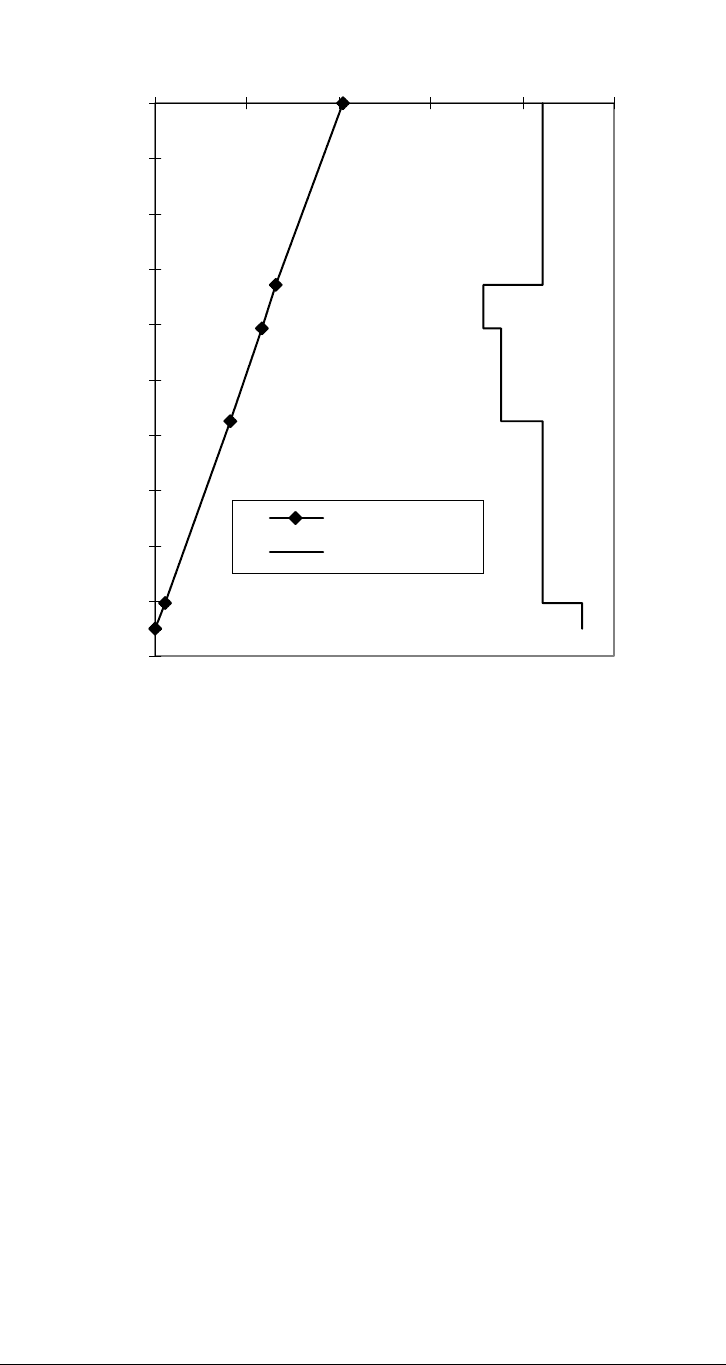
The axial load check in this example will be simple. We will assume that a

connection as strong as the tube body is to be considered. Figure 9-5

summarizes the axial load design procedure. Plotting design axial load versus

depth involves two steps:

1. Compute the axial tension at each depth as the weight in air of casing below

that point.

2. Apply the design factor for this load case to the axial tension. In this

particular design the tension design factor is the Chevron default of 1.5.

9-26 Casing/Tubing Design Manual

October 2005

1000

2000

3000

4000

5000

6000

7000

8000

9000

10000

0 200000 400000 600000 800000 1000000

Axial Load (lb)

TVD (ft)

Load w/DF

Burst Design

29,N

26,N

32,N

29,N

26,K

Figure 9-5. Axial Load Design for Production Casing Example

At every depth the current design is adequate and no further changes need be

made.

9.5.1.4 Qualitative Considerations

As it now exists, the preliminary design string is adequate to meet all design

loads from the preliminary design. The string is not, however, practical. Additional

points worth considering are covered in the sections to follow. In each case,

altering the current string description will increase the cost of the design. The

decision to implement the change is based on an assessment of the risk of

operational problems should the design proceed as is.

9.5.1.5 Minimum Segment Length, Number of Segments

A design that looks good on paper may not look good sitting on the pipe rack at

the well site. A large number of weight/grade and, possibly, thread combinations

can complicate field operations. Here are some design considerations:

• Manipulating the combinations to ensure the tubes are on the rack in the

correct running order is both time consuming, particularly offshore where

space is cramped and error prone.

• Having the same weight of tube, but different grades, means tube markings

must be clear and clearly understood.

Casing/Tubing Design Manual 9-27

October 2005

• Varying the threaded connection from string section to string section

increases the number of crossovers and backups needed. For some

connection designs, crossovers are required on a change in wall thickness

even if the connection type is unchanged.

The primary danger is running the wrong weight/grade/thread combination out of

order and placing it in a section of the string for which it has inadequate strength.

With exceptional cases possible, no more than three weight/grade combinations

should be run on onshore wells, and usually only one weight/grade should be run

offshore.

One method of limiting the number of sections in a design string is to designate a

minimum segment length. In fact, such a stipulation could have been appended

to the preliminary design procedure above. In such a case, each time a new

weigh/grade/thread combination is added, some minimum length of this

combination is run before another less expensive alternative is considered.

According to the design conditions, such a procedure can significantly complicate

a hand design, but is an insignificant addition to computer software.

In the current design, even assuming the same threaded connection throughout,

we have four weight/grade combinations to be run in five distinct sections. This is

too many to be practical. A number of change options exist, but probably the

most straightforward is to replace the 38.69-kg/m (26-ppf) K-55 with 38.69-kg/m

(26-ppf) N-80. This change has minimal effect on cost, but eliminates the

possibility of confusing grades at the well site. The amended design is shown in

Table 9-13.

Table 9-13. Production Casing Following Reduction in Sections

Weight kg/m

(lb/ft)

Grade Interval m (ft) Length m (ft)

43.16

(29)

N-80 0-1,006

(0-3,300)

1,006

(3,300)

38.69

(26)

N-80 1,006-1,756

(3,300-5,760)

750

(2,460)

43.16

(29)

N-80 1,756-2,749

(5,760-9,020)

994

(3,260)

47.62

(32)

N-80 2,749-2,896

(9,020-9,500)

146

(480)

9.5.1.6 Gauge Rings

Collapse considerations often dictate that a higher wall thickness casing is run at

the bottom of the string. In this regard, it is common practice to run one or two

joints of this higher wall thickness casing out of sequence at the top of the string.

This avoids the embarrassment (and lost rig time) of running a tool entirely to

bottom before discovering that it will not pass through the higher wall thickness

tube. Although gauge rings are a good idea, they should only be run with due

consideration given the following:

• An extra crossover may be required.

• A check should be made to ensure the gauge tube is of adequate strength.

For example, the gauge tube may be of high wall thickness, but of low grade,

9-28 Casing/Tubing Design Manual

October 2005

and may actually be weaker than a higher grade tube originally intended for

the upper extremity of the wellbore.

• Care should be exercised if, below the gauge ring, plans are to run a tubing

or other hanger in a lighter tube. Hangers are often designed to work in a

range of tube inside diameters. If, however, the discrepancy between the

gauge ring and the tube at the hanger depth is sufficient, it may be that a

hanger sufficiently small to pass the gauge ring will not anchor properly in the

larger inside diameter below. One remedy is to replace the gauge ring, and

the deeply set tube it represents, with a smaller wall thickness, higher grade

tube having the same performance properties.

In the current design, the 47.62-kg/m (32-ppf) tube at the bottom of the string

suggests a gauge ring (two joints) of this tube should be run at the top of the

string.

9.5.2 Final Design Check

With a preliminary design in hand, we are now in a position, with all geometries

given, to check the design for the effect of changing environment. The procedure

is in two steps:

1. Determine the initial state of the casing string. The initial state is that state

existing immediately following WOC.

2. One-by-one, submit the casing to the changes in environment associated

with each load case. The differential pressure loads will be identical to those

considered in the preliminary design. Changes in pressure and temperature

will, however, change the axial load. This affects not only the axial design,

but also collapse and burst resistance. In addition, changes in the axial load

may initiate column buckling, which introduces bending stress, even in a

vertical wellbore.

In the final design check, burst and axial yield of the tube body are considered

simultaneously by using the von Mises yield check. The API offers no correction

to burst or internal pressure resistance for the presence of axial load. The von

Mises yield check remedies this oversight. See Table 9-14 for casing string

examples.

Table 9-14. Example Production Casing String (Top to Bottom)

Segment Attribute Symbol Metric English

1 Length

1,006 m 3,300 ft

Outside Diameter

177.8 mm 7 in

Wall Thickness

10.36 mm 0.408 in

Grade (Minimum

Yield Strength)

551.6 MPa 80,000 psi

Weight with

Connection

43.16 kg/m 29 lb/ft

Connection Joint

Efficiency

100% 100%

Radial Clearance

19.49 mm 0.768 in

Casing/Tubing Design Manual 9-29

October 2005

Segment Attribute Symbol Metric English

2 Length

750 m 2,460 ft

Outside Diameter

177.8 mm 7 in

Wall Thickness

9.19 mm 0.362 in

Grade (Minimum

Yield Strength)

551.6 Mpa 80,000 psi

Weight with

Connection

38.69 kg/m 26 lb/ft

Connection Joint

Efficiency

100% 100%

Radial Clearance

19.49 mm 0.768 in

3 Length

73.2 m 240 ft

Outside Diameter

177.8 mm 7 in

Wall Thickness

10.36 mm 0.408 in

Grade (Minimum

Yield Strength)

551.6 Mpa 80,000 psi

Weight with

Connection

43.16 kg/m 29 lb/ft

Connection Joint

Efficiency

100% 100%

Radial Clearance

19.49 mm 0.768 in

4 Length

920 m 3,020 ft

Outside Diameter

177.8 mm 7 in

Wall Thickness

10.36 mm 0.408 in

Grade (Minimum

Yield Strength)

551.6 Mpa 80,000 psi

Weight with

Connection

43.16 kg/m 29 lb/ft

Connection Joint

Efficiency

100% 100%

Radial Clearance

19.49 mm 0.768 in

5 Length

146 m 480 ft

Outside Diameter

177.8 mm 7 in

Wall Thickness

11.51 mm 0.453 in

Grade (Minimum

Yield Strength)

551.6 Mpa 80,000 psi

Weight with

Connection

47.62 kg/m 32 lb/ft

Connection Joint 100% 100%

9-30 Casing/Tubing Design Manual

October 2005

Segment Attribute Symbol Metric English

Efficiency

Radial Clearance

19.49 mm 0.768 in

9.5.3 Cemented Casing versus Packer

Completions

The sections to follow compute the effects of changes in the temperature and

pressure environment on the integrity of the example casing string. Several

differences should be noted between these calculations and those of a packer

completion:

• The uncemented interval knows nothing of changes occurring below the

cement top. In a packer completion, pressure and fluid density changes

affect the pressure at the packer altering the axial load at the packer which is

consequently transmitted to the tubular string above the packer. In a

cemented completion, and following the setting time for the cement, it is

assumed that axial loads below the cement top are absorbed by the shear

bond between the casing and cement sheath. Therefore, loads generated

below the cement top have no effect on portions of the tubular string above

the cement top.

• The uncemented and cemented portions of a casing string must be handled

separately. In a packer completion, the entire extent of the tubing string

above the packer acts as an elastic unit, with each position in the string

experiencing the effects of the elastic response of its neighbors, even its

distant neighbors. This is also the case above the cement top in a casing

string. Below the cement top, however, each position is isolated from its

neighbors and must absorb the consequences of its inability to move axially.

Below the cement top, temperature and pressure changes have local affects

specific to the depth at which they occur.

As an example, consider a position in a tubular string that undergoes a local

temperature increase. If the string is completed with a packer or if the string is

casing above the cement top, the force generated by the tendency of the tube to

expand axially is distributed over the entire (laterally) unsupported length. If, on

the other hand, the string is cemented, the locale at which the temperature

change occurs is solely responsible for responding to the force generated by the

potential expansion.

Of course, in reality, the cement sheath is also elastic and any local effects, such

as those described above, would dissipate over a few diameters of axial length.

Such stress distributions, however, are beyond the scope of classic casing

design. In conventional design calculations, both the cement stiffness and the

shear bond between the cement and tubular are taken to be infinite in magnitude.

Cement plays a unique role in casing design calculations. The cement is

considered in the suite of initial fluids and its density is used when computing the

hydrostatic load at the bottom of the casing during cement setting. However, the

mud in which the casing is set (usually the mud displaced by the cement) or,

alternately, pore pressure is used to compute the external fluid gradient in load

Casing/Tubing Design Manual 9-31

October 2005

conditions. The assumption is that the cement solidifies sufficiently to restrain the

casing axially, but it is not competent to provide a permanent fluid seal to isolate

the casing from formation pressures (sometimes approximated by the displaced

mud).

One area of continuing controversy in cemented casing design regards the

contribution of the cement slurry density to the hydrostatic environment of the

casing during WOC. Field measurement indicates that during cement thickening

and solidification, the hydrostatic pressure within the slurry approaches the

adjacent pore pressure. This would suggest that, below the cement top, pore

pressure rather than cement slurry density should be used to compute the

hydrostatic pressure acting at the bottom of the casing string. Unfortunately, it is

not clear at what point the cement offers sufficient resistance to stop axial

movement of the casing and, therefore, set the initial state. Here, it will be

assumed that the density of the cement slurry fixes the hydrostatic load at the

bottom of the casing string and, thus, the initial axial load. Using pore pressure,

however, is acceptable as a matter of local or personal design preference.

9.5.3.1 Initial Conditions

The initial state of the casing immediately following WOC is summarized in Table

9-15.

Table 9-15. Conditions Immediately Following Installation

Segment Attribute Symbol Metric English

1 Internal area

1.938x10

30.04 in

External area

2.483x10

38.48 in

Moment of inertia

1.918x10

46.07 in

Axial force at bottom

434.01 kN 97,563 lb

Effective force at bottom

543.56 kN 122,187 lb

Internal pressure at

bottom

20.09 Mpa 2,914 psi

External pressure at

bottom

20.09 Mpa 2,914 psi

Effective weight

32.05 kg/m 21.53 lb/ft

Average temperature

ave

31.4°C 88.5°F

2 Internal area

1.996x10

30.94 in

External area

2.483x10

38.48 in

Moment of inertia

1.736x10

41.70 in

Axial force at bottom

161.16 kN 36,227 lb

Effective force at bottom

331.99 kN 74,628 lb

Internal pressure at

bottom

35.07 Mpa 5,087 psi

9-32 Casing/Tubing Design Manual

October 2005