Cain G., Meyer G.H. Separation of Variables for Partial Differential Equations: An Eigenfunction Approach
Подождите немного. Документ загружается.


page_252
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_252.html[22/02/2009 23:54:15]
< previous page page_252 next page >
Page 252
8.3)In Example 8.6 find a piecewise linear function
f(x)
such that
Find the interface problem satisfied by
and solve it in terms of eigenfunctions
discussed in Section 3.3.
8.4)Find the solution of
Plot the approximate Green’s functions of Example 8.13 for
(ξ, η)
=(.95, .95) and various
M
=
N=
10,
20, 100 as well as the analytic Green’s function
over the square minus a disk of radius centered at (.95, .95). Comment on the quality of the
approximations.
8.5)Let the boundary condition
hold on the boundary of the rectangle
D=
(0,
a
)×(0,
b
). Assume that
c
1 and c2 are constant along
the sides of
D,
and that
u, ux, uy,
and
uxy
are continuous on
∂D
at
(a, b)
. Show that the two
boundary equations and their first derivatives are consistent at
(a, b)
if and only if condition (8.8)
holds.
8.6)State and prove an analogue of Theorem 6.13 for the problem
Δ
w=F
in
D=
(0,
a
)×(0,
b
)
w=
0 on
∂D
.
< previous page page_252 next page >

page_253
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_253.html[22/02/2009 23:54:16]
< previous page page_253 next page >
Page 253
8.7) Find an eigenfunction solution of the biharmonic problem
when it is written in the form
(cf. Example 7.9).
8.8) Write out in detail the steps required for an eigenfunction solution of the problem
< previous page page_253 next page >

page_254
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_254.html[22/02/2009 23:54:16]
< previous page page_254 next page >
Page 254
This page intentionally left blank.
< previous page page_254 next page >

page_255
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_255.html[22/02/2009 23:54:17]
< previous page page_255 next page >
Page 255
Chapter 9
Multidimensional Problems
The algorithm of Chapter 5 requires linearly independent, preferably orthogonal, eigenfunctions but
otherwise is independent of the dimension of the eigenvalue problem. Employing the eigenf unctions for
the Laplacian in the plane we shall solve in broad outline some representative diffusion, vibration, and
potential problems involving two- and three-space dimensions.
9.1 Applications of the eigenfunction expansion method
Example 9.1 A diffusive pulse test.
We consider the inverse problem of determining a diffusion constant
A
such that the solution
u(x, y, t)
of
at the point
(x, y)=
(2, 3) assumes its maximum at time
t=
2.
As in Example 8.13 the calculations are formal but can be made rigorous when the
δ
-functions are
thought of as the limit of piecewise linear continuous functions.
We know from Example 8.12 that the eigenvalue problem
ΔΦ=
μ
Φ
in D
Φ=0 on
∂D
< previous page page_255 next page >

page_256
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_256.html[22/02/2009 23:54:18]
< previous page page_256 next page >
Page 256
has the eigenfunctions
with corresponding eigenvalues
The approximating problem is
where
The problem is solved by
where
It follows from the variation of parameters solution that
Hence we need to determine
A
such that
assumes its maximum at
t=
2. For a given
A
the function
uMN
(2, 3,
t
) is readily evaluated so that the
value
t
max
(A)
can be found where it achieves its maximum. Since
tmax(A)
is monotonely decreasing
with increasing
A,
it then is simple to search for
A
* such that
t
max
(A*)
=2. A search over
with
dt=
.01 and
dA
=.005 yields the results
< previous page page_256 next page >
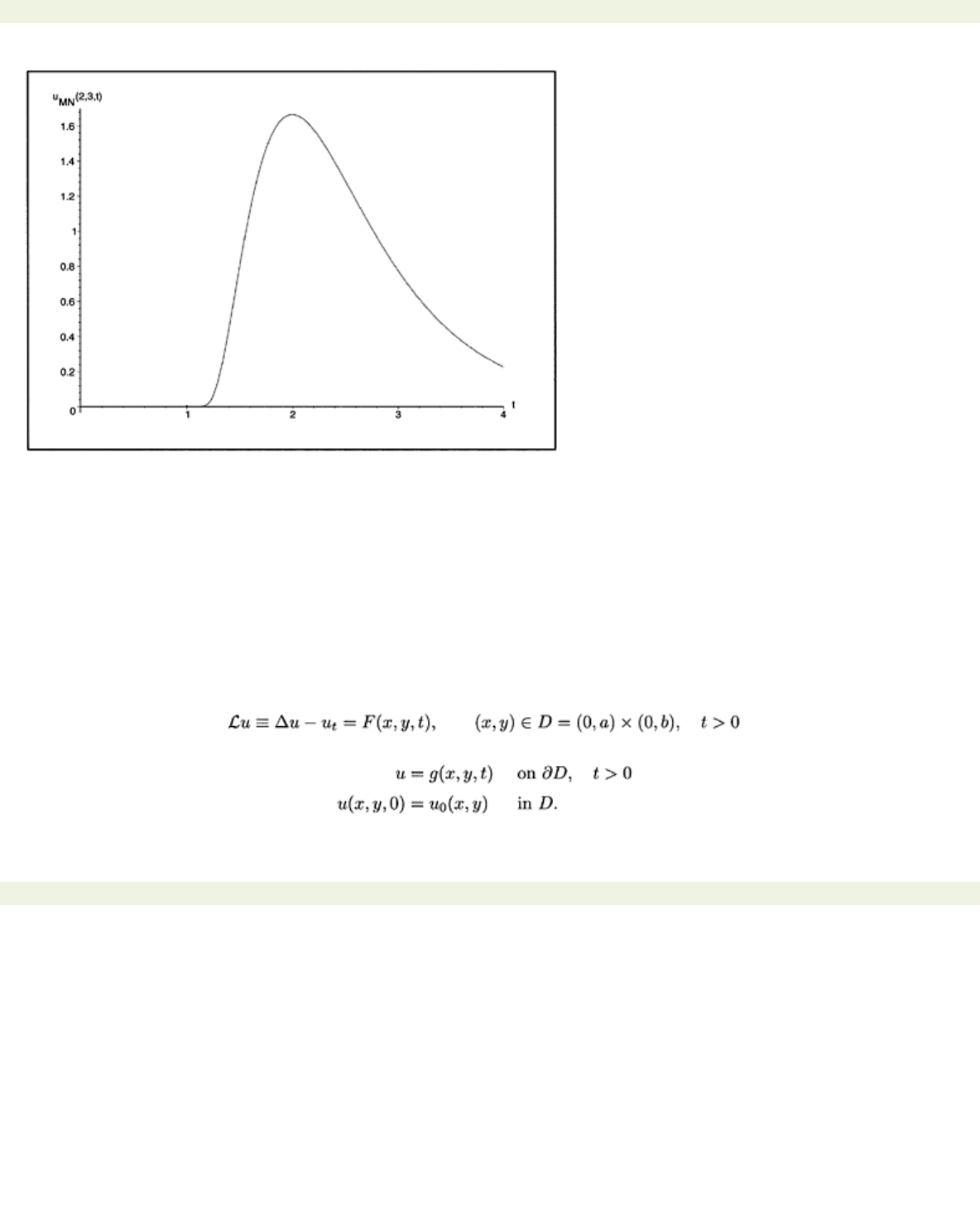
page_257
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_257.html[22/02/2009 23:54:18]
< previous page page_257 next page >
Page 257
Figure 9.1: Pulse
uMN
(2, 3,
t
) for the diffusion constant
A*=
.775 found with a bisection method.
M=
N=
90.
M=N
12 .775
50 .775
90 .775
A plot of the pulse
uMN
(2, 3
, t
) for
A*=
.775 is shown in Fig. 9.1 for
M
=
N
= 90. While
A*
appears to be
computable from relatively few terms, the pulse itself requires many more terms to adequately
approximate the
δ-
functions.
For a problem with different homogeneous boundary data new eigenfunctions for the Laplacian are
needed, but their computation along the lines of Example 8.12 is straightforward. A more involved
problem arises when the boundary data are not homogeneous. Consider, for example, the general
Dirichlet problem
If
g
is smooth in
D
for
t >
0, then rewriting the problem for
w=u−g
yields a new Dirichlet problem with
zero boundary data. If
g
is only smooth on
∂D,
< previous page page_257 next page >

page_258
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_258.html[22/02/2009 23:54:19]
< previous page page_258 next page >
Page 258
then we can define
and verify that
v=g
on
∂D.
Then
w=u−v
again will be the solution of a Dirichlet problem with zero
boundary data, but with a new source term
and the new initial condition
w
(
x, y,
0)=
u
0
(x, y)−v
(
x, y,
0).
For general boundary data of the third kind one can treat
t
as a parameter and solve
Then
w=u—v
will be subject to homogeneous boundary data, a new source term
G(x, y, t)=F(x, y, t)
+
vt(x, y, t)
and the initial condition
w
(
x, y,
0)=
u
0(
x, y)
−
v
(
x, y,
0).
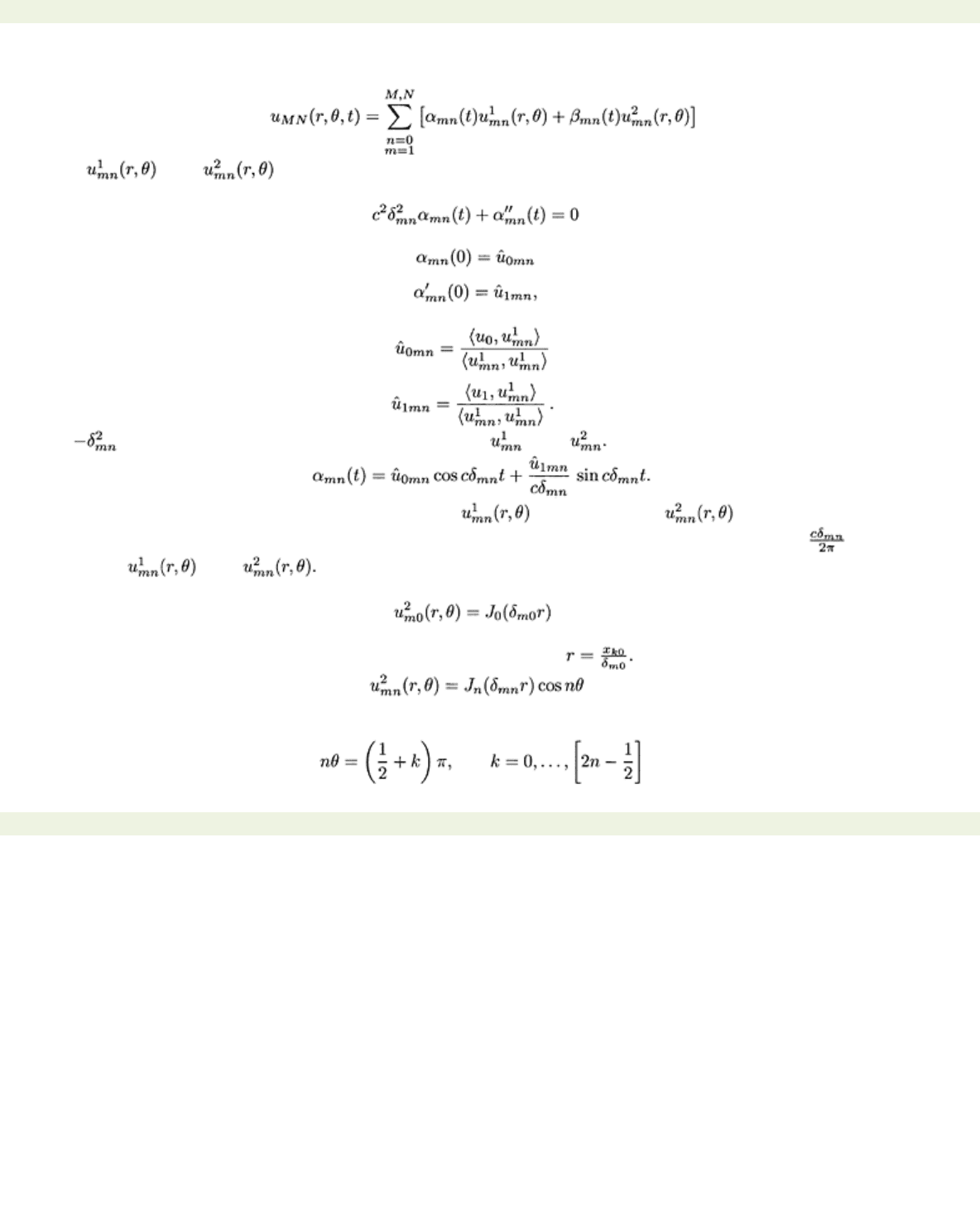
Example 9.2 Standing waves on a circular membrane.
It follows from the general theory that the solution of the initial value problem for a clamped circular
vibrating membrane
< previous page page_258 next page >
page_259
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_259.html[22/02/2009 23:54:20]
< previous page page_259 next page >
Page 259
can be approximated by
where and are eigenfunctions for the Laplacian on a disk found in Example 8.14.
The expansion coefficient
αmn(t)
satisfies
with
Here denotes the eigenvalue corresponding to and It follows that
The same equations hold for
βmn(t)
except that is replaced by in the initial conditions
for
βmn (t).
Thus
uMN
is the superposition of standing waves oscillating with frequency and
amplitudes and The amplitude is zero wherever the eigenfunction has a zero. For
example
is zero at
δm
0
r
=
xk
0 for
k=
1,…, m where xk0 is the kth zero of the Bessel function
J
0
(x)
. The nodes of
the standing waves are circles on the membrane with radius For
n
> 0 we see from
that the Bessel function
Jn
contributes m circular nodes with radius
δmnr
=
xkn, k
=1,…,
m,
while the
factor cos
nθ
contributes nodes of zero amplitude along the rays
< previous page page_259 next page >

page_260
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_260.html[22/02/2009 23:54:21]
< previous page page_260 next page >
Page 260
where
[a]
denotes the largest integer less than or equal to a. Similarly, is the
amplitude of a standing wave which vanishes wherever the Bessel function or sin
nθ
is zero. For
illustration the nodal lines for
are shown in Fig. 9.2.
Figure 9.2: Nodes of the standing wave
Example 9.3 The potential inside a charged sphere.
Consider the problem
where is the outward unit normal to the sphere of radius
R,
and are two given vectors in
and
a
+=max(
a,
0). In spherical coordinates the formulation is (see Section 1.3)
Since we already know the eigenfunctions and eigenvalues for the Laplacian on the surface of the unit
sphere, we can write an approximate solution in the form
< previous page page_260 next page >

page_261
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_261.html[22/02/2009 23:54:22]
< previous page page_261 next page >
Page 261
where
with
The same differential equation and similar boundary conditions apply to
βmn(r)
.
It is straightforward to verify that
Similarly
The problem is solved once the Fourier coefficients
αmn(R)
and
βmn(R)
are found. For their calculation
the formula
may prove helpful [1].
Example 9.4 Pressure in a porous slider bearing.
The following interface problem is a simplification of the mathematical model we found in [17] for the
analysis of a tapered porous slider bearing. It is included here to show how the two eigenfunction
expansion methods of Example 8.13 can be combined to yield a solution
{u(x, y),v(x, y, z)}
of the
following equations:
In addition we require
< previous page page_261 next page >
