Cain G., Meyer G.H. Separation of Variables for Partial Differential Equations: An Eigenfunction Approach

Подождите немного. Документ загружается.

page_242

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_242.html[22/02/2009 23:54:07]

< previous page page_242 next page >

Page 242

where

is the fundamental solution of Laplace’s equation in

and where is a smooth solution of the Dirichlet problem

The Dirchlet problem for is, of course, almost a model problem for an eigenfunction expansion

solution. Note that the boundary function is not defined and smooth on

because of the singularity at

(x, y)=(ξ, η)

is smooth on

∂D

and one could subtract the boundary values on opposite sides to zero

out the boundary data at, say

0 and

1, and solve the problem. However, for

(ξ, η)

=(.5, .5) the

symmetry of the problem suggests preconditioning the problem with (8.4) and solving the new problem

with a formal splitting. This way no new source terms arise, and the two problems of the splitting are

symmetric in

and

. The eigenfunction solution is very accurate so that the computed

accepted as the analytic Green’s function

(

x, y,

.5, .5).

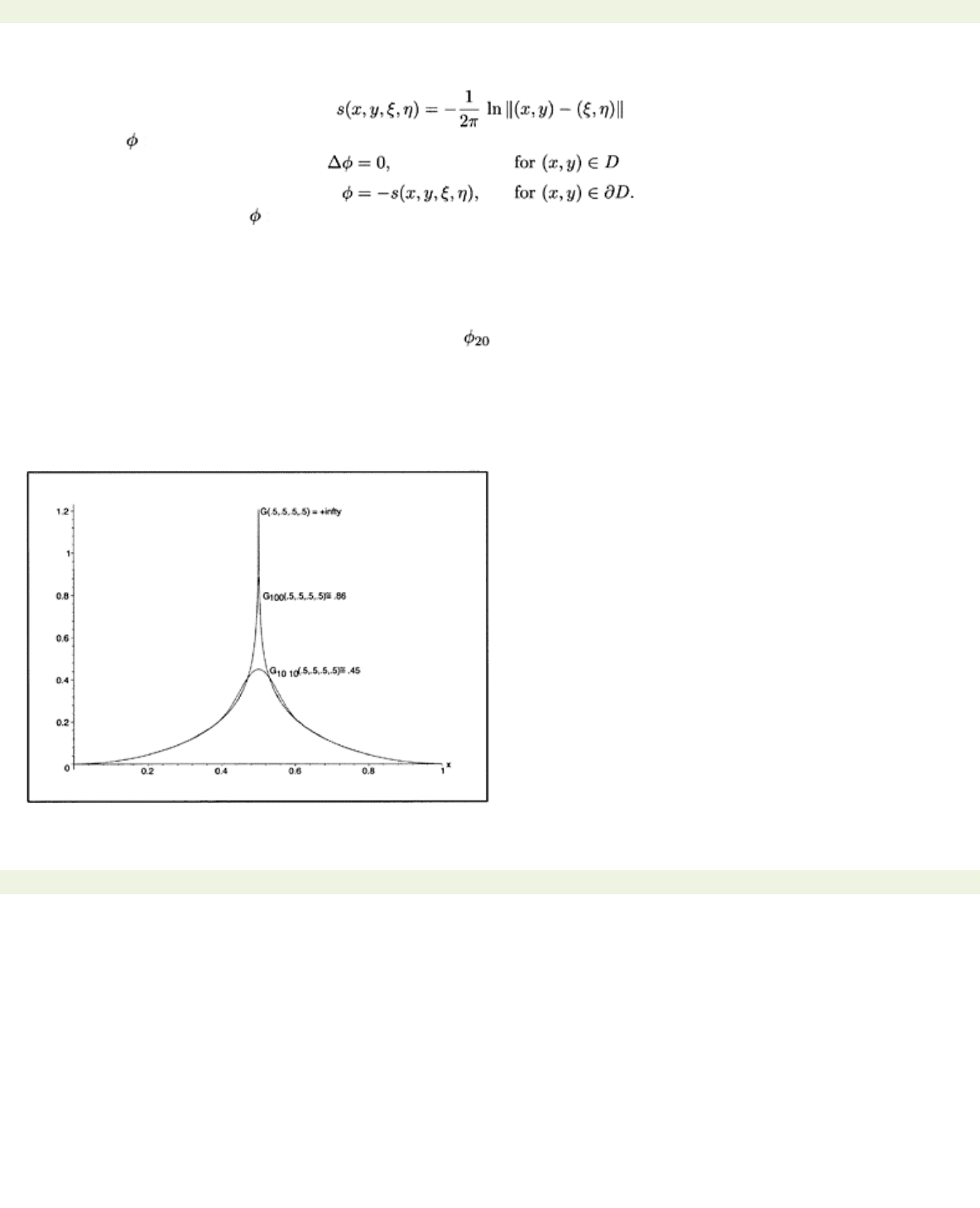
Fig. 8.13 shows a plot of the three approximate Green’s functions

10 10(

x, y,

.5, .5),

100(

x, y,

.5,

.5), and

(

x, y,

.5, .5) along the diagonal

x=y

The agreement between

and

appears very

good, particularly in view of the common use of Green’s functions under an integral. A plot of the

Green’s function approximation

GMN

for

M=N=

100 (not shown) yields a Green’s function approximation

indistinguishable from G100.

Figure 8.13: Green’s functions

and approximations

10 10

, G

100) for the Laplacian on a square.

Shown are

(

x, x,

.5, .5) and its approximations.

< previous page page_242 next page >

page_243

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_243.html[22/02/2009 23:54:08]

< previous page page_243 next page >

Page 243

Example 8.14 The eigenvalue problem for the Laplacian on a disk.

We wish to find the eigenvalues and eigenvectors of

(r, θ)=−

δ2u(r, θ)

on 0≤

r<R

u(R, θ)

=0,

where

=−

The problem in polar coordinates is

(8.22)

The associated one-dimensional eigenvalue problem is again the periodic problem in

given by

It has the eigenvalues For

=0 the eigenfunction is

(θ)=

For all other eigenvalues we obtain the two eigenfunctions

For each eigenfunction

and

ψn(θ)

we shall find all eigenfunctions of the Laplacian of the form

Substitution into the eigenvalue equation (8.22) shows that

α(r)

and

β(r)

must satisfy

< previous page page_243 next page >

page_244

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_244.html[22/02/2009 23:54:09]

< previous page page_244 next page >

Page 244

and

α(R)=β(R)=

0. For a given integer

this equation is known to be Bessel’s equation. Let us pick an

arbitrary integer

Then we have the two general solutions

α(r)=cn

Jn(δr)

cn2Yn(δr)

β(r)=dn

Jn(δr)+dn

Yn(δr).

Finiteness at

=0 requires that

2=0 and since eigenfunctions are only determined up to a

multiplicative constant, we shall set

Jn(δR)=

0 then demands that

δR

be a root of the

Bessel function

Jn(x).

Let

xmn

denote the mth nonzero root of the Bessel function

Jn(x).

We write

and obtain the solutions

αm(r)

βm(r)=Jn(δmnr)

It follows that the Laplacian on a disk has countably many eigenvalues

and the associated eigenfunctions

and

Example 8.15 The eigenvalue problem for the Laplacian on the surface of a sphere.

We want to find the eigenvalues and eigenfunctions of

=−

where

is the surface of a sphere of radius

It is natural to center the sphere at the origin and express the surface points in spherical coordinates

< previous page page_244 next page >

page_245

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_245.html[22/02/2009 23:54:09]

< previous page page_245 next page >

Page 245

for

Then

=−

becomes

We can rewrite this equation as

where for convenience we have set

The eigenfunctions are 2

periodic in θ and need to remain finite at the two poles of the sphere where

and The associated one-dimensional eigenvalue problem is

Φ″

(θ)

=−

2Φ

(θ)

=Φ(2π), Φ′

(θ)

−Φ′(2π).

In general there are two linearly independent eigenfunctions

n(θ)

=sin

nθ, n

=1, 2,…

n(θ)

=cos

nθ, n

=0, 1, 2,…

corresponding to the eigenvalue Again, we shall look for all eigenfunctions of the Laplacian of

the form

Substitution into the eigenvalue equation shows that a and

must satisfy

This equation is well known in the theory of special functions where it is usually rewritten in terms of

the variable An application of the chain rule leads to the equivalent equation

< previous page page_245 next page >

page_246

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_246.html[22/02/2009 23:54:10]

< previous page page_246 next page >

Page 246

The same equation holds for

β(z).

This equation is called the “associated Legendre equation.” It is

known [1] that it has solutions which remain finite at the poles

±1 if and only if

(

+1) for

≥0

in which case the solution is the so-called “associated Legendre function of the first kind”

For the

special case of n=0 the corresponding associated Legendre function is usually written as

Pm(z)

and is known as the

th order Legendre polynomial. The Legendre polynomials customarily are scaled

so that

(1)=1. For

≤ 3 they are

The associated Legendre functions of the first kind are found from

or alternatively, from

This expression shows that

(We remark that the second fundamental solution of the associated Legendre equation is the associated

Legendre function of the second kind. However, it blows up logarithmically at the poles, i.e., at

±1,

and will not be needed here.) Returning to our eigenvalue problem we see that for each

n≥

0 there are

countably many eigenvalues and eigenfunctions

These eigenfunctions are mutually orthogonal on the surface of the sphere so that

unless

k, n=ℓ,

and

i=j.

Here

< previous page page_246 next page >

page_247

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_247.html[22/02/2009 23:54:11]

< previous page page_247 next page >

Page 247

Since the one-dimensional eigenfunctions {Φn(

θ), Ψn(θ)

} are orthogonal in

2(0, 2π), it follows that

are orthogonal in i.e., that

(Since

Pm(z)

is an

th order polynomial, this implies that is an orthogonal basis in

2(−1,

1) of the subspace of

th order polynomials.) Moreover, it can be shown that

8.3 Convergence of

uN(x, y)

to the analytic solu tion

In Chapter 1 we pointed out that the maximum principle can provide an error bound on the pointwise

error

u(x, y)−uN(x, y)

in terms of the approximation errors for the source term and the boundary data.

An application of these ideas is presented in Chapter 6 for the diffusion equation. We shall revisit these

issues by examining the error incurred in solving Poisson’s equation on a triangle as described in

Example 8.11.

We recall the problem: the solution

of the problem

where

is a triangle with vertices (0, 0), (3, 0), (2, 1), is approximated with the solution

of the

problem

i.e.,

0 on

θ=

1, where

tan−1 .5, and

where

uN (r(θ), θ)

is obtained from the least squares minimization.

1 is the projection in of

f(θ)

=1 into span {sin

λnθ

Since

is an exact solution of Poisson’s equation in

we can write

uN(x, y)=u

N(x, y)+u

N(x, y)

< previous page page_247 next page >

page_248

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_248.html[22/02/2009 23:54:12]

< previous page page_248 next page >

Page 248

where

1 in

=0 on

∂T,

=0 in

N=uN(x, y)

∂T.

Our goal is to estimate the error

u−uN=(u−u

N)−u

As a solution of Laplace’s equation

must assume its maximum and minimum on

∂T.

Hence

However

because

0 for

θ=

0. The failure of

1 to converge uniformly precludes an application of the

maximum principle to estimate

(u−u

We know from the Sturm-Liouville theorem (and Chapter 4) that

1 converges to in the

norm. This implies the inequality

because

r(θ) ≤

We employ now a so-called energy estimate. Let us write

w=u−u

Then

is an analytic solution of

−PN

1 in

0 on

∂T.

It follows from the divergence theorem and the fact that

=0 on

∂T

that

i.e., that

(8.23)

< previous page page_248 next page >

page_249

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_249.html[22/02/2009 23:54:13]

< previous page page_249 next page >

Page 249

For any point

we can write

where the last inequality comes from Schwarz’s inequality applied to Since

≤1 for all

integration over

yields the Poincaré inequality

(8.24)

If we also apply Schwarz’s inequality to the right side of (8.23), we obtain from (8.23), (8.24) the

estimate

The pointwise bound on |

implies

The actual approximation error is then bounded by

For the computed solution of Example 8.14 we observe for

=15

and a simple calculation shows that

Obviously,

15 is much too small to give a tight bound on the actual error (see also the discussion on

p. 56). The need for many terms of the Fourier expansion to overcome the Gibbs phenomenon has

arisen time and again and applies here as well, but the computed solutions

do not appear to change

noticeably for larger

We shall end our comments on convergence by pointing out that the error estimating techniques familiar

to finite element practitioners also apply to eigenfunction expansions. To see this we shall denote by

the solution of the model problem

(0,

)×(0,

)

0 on

∂D.

< previous page page_249 next page >

page_250

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_250.html[22/02/2009 23:54:14]

< previous page page_250 next page >

Page 250

The approximate solution is

where

and where

solves

PNF

=0 on

∂D.

Let

where

β(y)

is any smooth function such that

(0) =

β(b)

=0. Let and || ||

denote inner product and norm in

and let us set

Then

(8.25)

because

due to the orthogonality of

in Because

is bilinear, we see that

A(u−uN, U−uN)=A(u−vN+vN−uN, U−uN)=A(u−VN, u−uN)

(8.26)

for any function

of the form

(8.27)

Schwarz’s inequality applied to (8.26) yields

We conclude that the error in the gradient is bounded by the error in the gradient of the best possible

approximation to

of the form (8.27). The error analysis now has become a question of approximation

theory. This view of error analysis is developed in the finite element theory where very precise

for

the error and its gradient are based on bounds for the analytic solution

and its derivatives known from

the theory of partial differential equations. The consequence for the eigenfunction expansion method is

that the error in

< previous page page_250 next page >

page_251

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_251.html[22/02/2009 23:54:14]

< previous page page_251 next page >

Page 251

our approximation is no larger than the error which arises when the (unknown) solution

u(x, y)

for the

above Dirichlet problem is expanded in a two-dimensional Fourier sine series

because this is an expression of the form (8.27).

Exercises

8.1)Solve

8.2)Consider the problem

i) Find an eigenfunction approximation of

applied to a formal splitting without preconditioning.

ii) Find an eigenfunction approximation of

applied to a formal splitting after preconditioning.

iii) Find an eigenfunction approximation of

after zeroing out the data on

0 and

iv) Find an eigenfunction approximation of

after zeroing out the data on

0 and

Discuss which of the above results appears most acceptable for finding the solution

of the original

problem.

< previous page page_251 next page >