Caffarelli L.A., Golse F., Guo Y. et al. Nonlinear Partial Differential Equations

Подождите немного. Документ загружается.

1.2. Integral diﬀusion and the quasi-geostrophic equation 23

Theideaisthat,ononehand,thefastcut-oﬀinZ will make the inﬂuence

of the tiny sides decay so much in X that at the level of the next cut-oﬀ (in X)

it will be wiped out by the dyadic cut-oﬀ in θ, while the contribution of the trace

will decay so fast (faster than M

−k

if we choose c

very small) that

∗

(X, δ

) ≤ θ

∗ P

≤θ



P



will also be wiped out by the consecutive truncation.

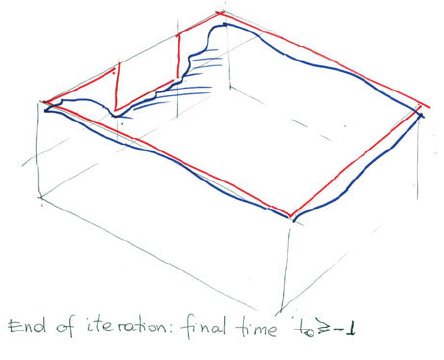
At the end of the process, at time t

, we have only information on the trace θ,

but we can go inwards by harmonicity to complete the proof.

1.2.7 First part

In this ﬁrst part, we prove that a solution θ between 0 and 2, with very small L

norm, separates from θ = 2 in a smaller cylinder.

Lemma 12. We assume that

v

∞

(−4, 0; BMO(R

))

+sup

−4≤t≤0





v(t, x) dx



≤ C

. (1.2.2)

Then there exist ε

> 0 and λ>0 such that, for every solution θ to (1.2.1),the

following property holds true: If we have θ

∗

≤ 2 in [−4, 0] × B

∗

and



−4



∗

(θ

∗

)

dx dz ds +



−4



(θ)

dx ds ≤ ε

then (θ)

≤ 2 − λ on [−1, 0] × B

24 Chapter 1. The De Giorgi Method for Nonlocal Fluid Dynamics

Proof. The proof follows the strategy discussed above. First, we introduce some

previous tools. Since the method was based on the control of θ

∗

by two harmonic

functions, one for the local data and the other for the far away, before starting the

proof we build two useful barriers.

Step 1: Barriers

The ﬁrst barrier is the following:

Barrier b

(x, z)

=2inz =1

=2in|x| =1

z =1/2

≤2 − 4λ< 2 b

=2in|x| =1

=0inz =0

Then b

has the following properties:

(i) b

is harmonic in B

∗

;

(ii) b

=2in∂B

∗

except z =0;

(iii) b

=0in∂B

∗

∩{z =0};

and, for some 0 <λ,wehaveb

≤ 2 − 4λ<2inB

∗

1/2

The barrier b

implies that

1.2. Integral diﬀusion and the quasi-geostrophic equation 25

The barrier b

satisﬁes the following:

= −1 x



7



7

z = ±δ

(i) b

is harmonic in D;

(ii) b

=0forz ± δ;

(iii) b

=1forx

= 1 and b

=0forx

= −1.

Then b

≤

C cos(z/δ) e

−(1−x

)/δ

. In particular, if 1 − x

= h  δ,wehave

≤

−h/δ

and

C =(cos1)

−1

Remark. Exponential decay also holds for D

by applying the Harnack in-

equality to the intervals I

= {k ≤ x

≤ k +1}.

Now we are ready to set the main inductive steps as discussed above. When

we do so, we will realize that we have to start the process for some advanced value

k of the step. So we will go back and do a ﬁrst large step to cover the starting of

the process.

Step 2: Setting of the constants

We recall that λ>0 is deﬁned by the fact that the barrier function satisﬁes that

< 2 − 4λ in B

∗

1/2

.Next,

C =(cos1)

−1

is the constant in the bound for the

barrier function b

. The smallness constant C

in the hypothesis of Lemma 12 will

be chosen later as C

(λ, M).

We need to ﬁx constants M for the rate of decay of the L

norm of the

truncation θ

and δ for the rate of decay of the support in z of θ

∗

We require:

(i) n

−(2δ)

−k

≤ λ2

−k−2

(with δ small so the side contribution is absorbed by

the cut-oﬀ);

(ii) δ

(Mδ

)

−k

P (1)

≤ λ2

−k−2

(with M (δ) large to keep the support of the

truncation in the δ

strip);

(iii) M

−k

≥ C

−(k−3)(n+1/n)

for k ≥ 12n (so that the inductive decay gives us

the fast geometric decay).

Here P (1) denotes the restriction of the Poisson kernel P (x, z)toz ≡ 1.

The choice is straightforward. We ﬁrst construct δ to verify the ﬁrst inequality

in the following way. If δ<1/4, the inequality is true for k>k

due to the

26 Chapter 1. The De Giorgi Method for Nonlocal Fluid Dynamics

exponential decay. If necessary, we then choose δ smaller to make the inequality

also valid for k<k

.Nowthatδ has been ﬁxed, we have to choose M large to

satisfy the remaining inequalities. Note that the second inequality is equivalent to





≤

λδ

4P (1)

It is suﬃcient to take

M ≥ sup



8P (1)

λδ



The third inequality is equivalent to





k/N

≥ M

3(1+1/N )

For this it is enough to take M ≥ sup(1,C

). Indeed, this ensures M

≥ M

and hence





k/N

≥ M

k/(2N)

≥ M

The main inductive step will be the following.

Step 3: Induction

We set

=(θ − C

)

with C

=2− λ(1 + 2

−k

). We consider a cut-oﬀ function in x only such that

1+2

−k−1

}

≤ η

≤ 1

1+2

−k

}

, |∇η

|≤C2

and we let



−1−2

−k



|∇(η

∗

dx dz dt +sup

[−1−2

−k

,1]



(η

)

dx dt.

We want to prove that, for every k ≥ 0,

≤ M

−k

, and (1.2.3)

∗

is supported in 0 ≤ z ≤ δ

(1.2.4)

(it vanishes at δ

, and thus we can extend it by zero).

Step 4: Starting the process

We prove in this step that, if ε

is small enough, then (1.2.3) is veriﬁed for 0 ≤ k ≤

12N, and that (1.2.4) is veriﬁed for k = 0. We use the energy inequality (1.2.1)

1.2. Integral diﬀusion and the quasi-geostrophic equation 27

with cut-oﬀ function η

(x)ψ(z)whereψ is a ﬁxed cut-oﬀ function in z only. Taking

the mean value of (1.2.1) in T

between −4and−2, we ﬁnd that (1.2.3) is veriﬁed

for 0 ≤ k ≤ 12N if ε

istakensuchthat

24N

(1 + φ)ε

≤ M

−12N

. (1.2.5)

We have used that |∇η

≤ C2

24N

for 0 ≤ k ≤ 12N. Let us consider now the

support property (1.2.4). By the maximum principle, we have

∗

≤ (θ

) ∗ P (z)+b

(x, z)

in R

×B

∗

,whereP (z) is the Poisson kernel. Indeed, the right-hand side function

is harmonic, positive, and the trace on the boundary is bigger than the one of θ

∗

From Step 1 we have b

(x, z) ≤ 2 − 4λ.Moreover,

θ

∗ P (z)

∞

(z≥1)

≤ CP (1)

√

≤ C

√

Choosing ε

small enough so that this constant is smaller than 2λ gives

∗

≤ 2 − 2λ for 1 ≤ z ≤ 2, t ≥ 0, x ∈ B

∗

=(θ

∗

− (2 − 2λ))

≤ 0 for 1 ≤ z ≤ 2, t ≥ 0, x ∈ B

Hence, η

∗

vanishes for 1 = δ

≤ z ≤ 2.

Step 5: Propagation of the support property (1.2.4)

Assume that (1.2.3) and (1.2.4) are veriﬁed at k. We want to show that (1.2.4) is

veriﬁed at (k + 1). We will also show that the following is veriﬁed at k:

k+1

∗

k+1

≤ [(η

) ∗ P (z)]η

k+1

on B

∗

, (1.2.6)

where

∗

= B

1+2

−k

× [0,δ

]. We want to control θ

∗

on this set by harmonic

functions taking into account the contributions of the sides one by one. Consider

1+2

−k−1/2

× [0,δ

]. On z = δ

we have no contribution thanks to the induction

property (1.2.4) at k (the trace is equal to 0). The contribution of the side z =0

canbecontrolledbyη

∗ P (z). (It has the same trace as θ

on B

1+2

−k−1/2

On each of the other sides we control the contribution by the following func-

tion of x =(x

,...,x

((x

− x

)/δ

,z/δ

)+b

((−x

+ x

−

)/δ

,z/δ

where x

=(1+2

−k−1/2

)andx

−

= −x

. Indeed, b

is harmonic, and on the side

and x

−

it is bigger than 2. Finally, by the maximum principle,

∗

≤



i=1



((x

− x

)/δ

,z/δ

)+b

((−x

+ x

−

)/δ

,z/δ

)



+(η

) ∗ P (z).

28 Chapter 1. The De Giorgi Method for Nonlocal Fluid Dynamics

From Step 1, for x ∈ B

1+2

−k−1



i=1



((x

− x

)/δ

,z/δ

)+b

((−x

+ x

−

)/δ

,z/δ

)



≤ 2N

−

−k

√

2+1)δ

≤ λ2

−k−2

(thanks to Step 2). This gives (1.2.6), since

∗

k+1

≤ (θ

∗

− λ2

−k−1

)

More precisely, this gives

∗

k+1

≤ ((η

) ∗ P (z) − λ2

−k−2

)

So,

k+1

∗

k+1

≤ ((η

) ∗ P (z) − λ2

−k−2

)

From the second property of Step 2, we ﬁnd that, for δ

k+1

≤ z ≤ δ

|(η

) ∗ P (z)|≤



P (z)

≤

−k/2

(k+1)N/2

P (1)

≤ λ2

−k−2

The last inequality makes use of Step 2. Therefore,

k+1

∗

k+1

≤ 0forδ

k+1

≤ z ≤ δ

Note, in particular, that with Step 4 this gives that (1.2.4) is veriﬁed up to k =

12N + 1 and (1.2.6) up to k =12N .

Step 6: Propagation of property (1.2.3)

We show in this step that if (1.2.3) is true for k − 3 and (1.2.4) is true for k − 3,

k − 2andk − 1, then (1.2.3) is true for k.

First notice that, from Step 5, (1.2.4) is true at k −2, k − 1, and k. We just

need to show that

≤ C

k−3

)

1+1/N

for k ≥ 12N +1, (1.2.7)

with

= C

1+2/N

2/N

. (1.2.8)

Indeed, if we do the third inequality of Step 2, this will give us the result.

1.2. Integral diﬀusion and the quasi-geostrophic equation 29

Step 7: Proof of (1.2.7)

Since η

∗

{0<z<δ

k−1

}

has the same trace at z = 0 as (η

)

∗

and the latter is

harmonic, we have



k−1



|∇(η

∗



∞



|∇(η

∗

{0<z<δ

k−1

}

≥



∞



|∇(η

)

∗



|Λ

1/2

(η

Note that we have used (1.2.4) in the ﬁrst equality. The Sobolev and H¨older

inequalities give

k−3

≥ Cη

k−3



2(N+1)/N

([−1−2

−k−3

,0]×R

)

From (1.2.6),

η

k−2

∗

k−2



2(N+1)/N

≤P (1)

η

k−3



2(N+1)/N

Hence,

k−3

≥ Cη

k−2

∗

k−2



2(N+1)/N

+ Cη

k−3



2(N+1)/N

≥ C



η

k−2

∗

k−1



2(N+1)/N

+ η

k−2

k−1



2(N+1)/N



Since η

is a cut-oﬀ function in x, and using (1.2.4), we have that η

∗

vanishes on

the boundary of B

1+2

−k

×[−δ

,δ

]. We can then apply the energy inequality (1.2.5)

on η

∗

{0<z<δ

k−1

}

. Taking the mean value of (1.2.5) in T

between −1 − 2

−k−1

and −1 − 2

−k

, we ﬁnd:

≤ C2

(φ +2)





k−1



k−1

∗



We have used here the fact that |∇η|

≤ C2

k−1

.Ifθ

> 0, then θ

k−1

≥ 2

−k

λ.

So,

{θ

>0}

≤

k−1

and

{η

k−1

>0}

{θ

>0}

≤

k−2

k−1

Therefore,



k−1



k−1

∗

≤

2k/N

2/N





(η

k−2

k−1

)

2(N+1)/N



(η

k−2

∗

k−1

)

2(N+1)/N



30 Chapter 1. The De Giorgi Method for Nonlocal Fluid Dynamics

and so

≤

k(2+2/N )

2/N

1+1/N

k−3

This gives (1.2.7), for C big enough compared to λ

2/N

. 

1.2.8 Second part

In the ﬁrst part, we have established that, if 0 ≤ θ

≤ 2 and its energy or norm is

very small in B

∗

,thenθ

≤ 2 − λ in B

, i.e., the oscillation of θ actually decays.

We now want to get rid of the “very small” hypothesis.

This second lemma (Lemma 13) proves that, if θ

≤ 0 “half of the time” and

it only needs very little room (say, δ)togofrom{θ

≤ 0} to {θ ≥ 1},itisbecause

(θ − 1)

has already very small norm to start with. This produces a dichotomy:

either the support of θ decreases substantially, or θ becomes small anyway, in the

same spirit as De Giorgi’s lemma.

Lemma 13. For every ε

> 0 there exists a constant δ

> 0 with the following

property: For every solution θ to (1.2.1) with v verifying (1.2.2),ifθ

∗

≤ 2 in Q

∗

and

|{(x, z, t) ∈ Q

∗

: θ

∗

(x, z, t) ≤ 0}| ≥

∗

then the following implication holds true: If

|{(x, z, t) ∈ Q

∗

:0<θ

∗

(x, z, t) < 1}| ≤ δ

then



(θ − 1)

dx dt +



∗

(θ

∗

− 1)

dx dz dt ≤ C

√

This lemma is, of course, the adapted version of the De Giorgi’s isoperimetric

inequality.

The idea of the proof is the following. We ﬁrst throw away a small set of

times for which I



∗

|∇u

∗

dx dz is very large:

≥

This is a tiny set of times:

|S|≤Cε

since



|∇u

∗

dx dz dt ≤ C

Outside of S,foreachtimet, the isoperimetric inequality is valid:

|A||B|≤|D| K/ε

1.2. Integral diﬀusion and the quasi-geostrophic equation 31

But for some t,sayt<−

,wemaychooseaslicewhere|A| >

and

|D|≤δ.Then|B|≤(64)

δK/ε

≤ Kε

if δ ∼ ε

. In particular, (θ − 1)

has

very small L

norm for that t: (θ −1)



≤ kε

. But the energy inequality then

controls the L

norm of (θ − 1)

into the future. We now give a more detailed

proof.

Proof. Take ε

 1. From the energy inequality and using that θ

∗

≤ 2inQ

∗

we get



−4



∗

|∇θ

∗

dx dz dt ≤ C.

Let

K =



|∇θ

∗

dx dz dt

Then





t :



∗

|∇θ

∗

(t) dx dz ≥ K





≤

. (1.2.9)

For all t ∈{t :



∗

|∇θ

∗

(t) dx dz ≤ K}, the isoperimetric inequality gives that

|A(t)||B(t)|≤|C(t)|

1/2

where

A(t)={(x, z) ∈ B

∗

: θ

∗

(t, x, z) ≤ 0},

B(t)={(x, z) ∈ B

∗

: θ

∗

(t, x, z) ≥ 1},

C(t)={(x, z) ∈ B

∗

:0<θ

∗

(t, x, z) < 1}.

Let us set δ

= ε

and

I =



t ∈ [−4, 0] : |C(t)|

1/2

≤ ε

and



∗

|∇θ

∗

(t) dx dz ≤ K



First we have, using the Chebyshev inequality,



{t ∈ [−4, 0] : |C(t)|

1/2

≥ ε

}



≤

|{(t, x, z):0<θ

∗

< 1}|

≤

≤ ε

/4.

Hence |[−4, 0] \I|≤ε

/2. Secondly, we get for every t ∈ I such that |A(t)|≥1/4,

|B(t)|≤

|C(t)|

1/2

|A(t)|

≤ 4Cε

5/2

≤ ε

. (1.2.10)

32 Chapter 1. The De Giorgi Method for Nonlocal Fluid Dynamics

In particular,



∗

(t) dx dz ≤ 4(|B(t)| + |C(t)|) ≤ 8ε

But



(t) dx =



∗

(t, x, z) dx − 2



∗

(t)∂

∗

dx d¯z

for any z. Therefore, integrating in z on [0, 1], we ﬁnd:



(t) dx ≤



∗

(t, x, z) dx dz +2

√





∗

(t) dx dz ≤ C

√

We want to show that |A(t)|≥1/4 for every t ∈ I ∩ [−1, 0]. First, since

|{(t, x, z):θ

∗

≤ 0}| ≥ |Q

∗

|/2,

there exists t

≤−1 such that |A(t

)|≥1/4. For this t



) dx ≤ C

√

Using the energy inequality, for any r>0(where∇η is of order 1/r)wehave,for

every t ≥ t



(t) dx ≤



) dx +

C(t − t

)

+ Cr.

Let us choose r such that

Cr + C

√

≤ 1/128.

So, for t − t

≤ δ

∗

= r/(128C), we have



(t) dx ≤

(Note that δ

∗

does not depend on ε

. Hence we can suppose ε

 δ

∗

.) Moreover,

∗

(z)=θ



∂

∗

d¯z ≤ θ

√





|∂

∗

d¯z



1/2

So, for t − t

≤ δ

∗

, t ∈ I and z ≤ ε

, we have, for each x,

∗

(t, x, z) ≤ θ

(t, x)+





∞

|∂

∗

d¯z



1/2

The integral, in x only, of the square of the right-hand side term is less than

1/8+C

√

≤ 1/4. So, by Chebyshev, for every ﬁxed z ≤ ε

|{x ∈ B

,θ

∗

(t, x, z) ≥ 1}| ≤