Caballero B. (ed.) Encyclopaedia of Food Science, Food Technology and Nutrition. Ten-Volume Set

Подождите немного. Документ загружается.

tbl0002 Table 2 Major drug–nutrient interactions of clinical relevance

Drug Class Food/nutrient Effect/mechanism

Acarbose Antidiabetic Food Delays carbohydrate breakdown: delays glucose

absorption

Iron Decreased iron absorption

Acetaminophen Analgesic Food May delay extended release; high-pectin food delays

absorption

Alcohol Increased risk of hepatotoxicity

Acetohexadmide Antidiabetic Glucose Hypoglycemia

Alcohol Flushing, headache, nausea, vomiting, sweating,

tachycardia

Sodium Hyponatremia, SIADH

Acyclovir Antiviral Food No effect; may take with meals

Aluminum hydroxide Antacid Thiamin Affects bioavailability, because of pH

Iron Decreased iron absorption

Phosphorus Inhibits phosphorus absorption

Vitamin A Inhibits vitamin A absorption

Amikacin Antibiotic Calcium, potassium,

magnesium

Causes renal wasting of these nutrients

Amoxicillin Antibiotic Food Decreased absorption by delayed gastric emptying

Amphotericin B Antifungal Potassium,

magnesium

Causes renal wasting of potassium and magnesium

Ampicillin Antibiotic Food Decreased absorption by delayed gastric emptying

Potassium High doses increase urinary potassium losses

Antipyrine Green vegetables,

beef protein

Decreased absorption

Aspirin Analgesic Food Decreased rate of absorption

Folic acid Increased excretion of folate

Amino acids Decreased intestinal absorption of amino acids,

increased urinary excretion of tryptophan

Iron Chronic high dose 3–4 g day

1

, iron deficiency possible

Alcohol Gastric irritation, leading to possible gastric bleeding

Curry powder,

licorice, teas,

raisins, paprika

Potential salicylate accumulation

Ascorbic acid,

vitamin C, fresh

fruits, high

vitamin C

Increased urinary excretion; decreased concentration in

serum and platelets

Astemizole Antihistamine Food Decreased bioavailability

Atenolol Antihypertensive Food Delayed absorption

Atovaquone Antibiotic Food Bioavailability increased, especially high-fat foods

Atropine Anticholinergic Iron Delayed absorption

Azithromycin Antibiotic Food Decreased rate and delayed absorption

Bacampicillin Antibiotic

(penicillins)

Food Decreased absorption

Barbiturates Anticonvulsant Alcohol Enhanced CNS depression

Calcium, vitamin D Increased vitamin D requirements, owing to increased

metabolism

Cyanocobalamin Increased bone resorption

Folic acid Decreased serum levels, leading to megaloblastic

anemia

Serum lipids Decreased CSF folate and erythrocyte concentration;

may increase cholesterol, HDL triacylglycerols

Benzodiazepines Anticonvulsant Nutrient Enhanced CNS depression

Clonazedam Calcium Increased vitamin D requirements, secondary to

increased metabolism

Clorazepate dipotassium Vitamin D Increased bone resorption

Lopazepam Cyanocobalamin Decreased serum levels, leading to megaloblastic

anemia

Oxazepam Folic acid Decreased CSF folate and erythrocyte concentration

Serum lipids May increase cholesterol, HDL triacylglycerols

Buprenorphone HCL Analgesic Alcohol Enhanced CNS depression

Narcotic

Agonist–antagonist

Continued

1906 DRUG–NUTRIENT INTERACTIONS

Drug Class Food/nutrient Effect/mechanism

Butorphanol tartate Analgesic Alcohol Enhanced CNS depression

Narcotic

Agonist–antagonist

Calcium carbonate Antacid Iron Decreased iron absorption

Fats May cause steatorrhea

Captopril Antihypertensive

angiotensin-

converting

enzyme inhibitor

Food Reduced absorption

Carbamazpine Anticonvulsant Sodium SIADH

Food Enhanced absorption, increased bile production

Carbenicillin iandanyl sodium Antibiotic Food Decreased rate of absorption

Cephalosporins Antibiotic General alcohol Flushing, headache, nausea, vomiting, tachycardia

Cefachlor Food Decreased rate of absorption

Cefadroxil Food No effect (may take food)

Cefamandole Vitamin K Decreased vitamin K hypoprothrombinemia

Cefixime Food Decreased rate of absorption

Cefoperazone Vitamin K Decreased vitamin K hypoprothrombinemia

Cefotetan Vitamin K Decreased vitamin K hypoprothrombinemia

Cefpodoxime proxetil Food Bioavailability increased with food

Ceftibuten Food Decreased absorption

Cefuroxim axetil Food Bioavailability increased with food

Cephalexin Food Absorption reduced for suspension; delayed for

capsules

Cephradine Food Rate of absorption delayed

Cetrizine Antihistamine Food Delays time to serum peak; no effect on overall

absorption

Chlorambucil Antineoplastic Food Reduced absorption

Chloramphenicol Antibiotic Iron Increased serum level iron; increased total iron-binding

capacity

Folic acid Antagonist to physiological action; increased

requirements of folic acid

Vitamin B

Increased requirements of vitamin B

can cause

peripheral neuropathy

Chloroquine Antimalarial Food Increased bioavailability

Chlorothiazide Diuretic Food Increased drug absorption owing to delayed gastric

emptying

Chlorpromazine Antiemetic Food Decreased absorption owing to delayed gastric

emptying

Chlorpropamide Antidiabetic Glucose Decreased blood glucose concentration

Sodium Hyponatremia, SIADH

Alcohol Flushing, headache, nausea, vomiting, tachycardia

Cholchicine Antigout Cyanocobalamin Decreased absorption of cyanocobalamin

Cimetidine Histamine 2

antagonist

Food Delays absorption

Ciprofloxacin Antibiotic

(quinolone)

Caffeine Decreased rate of absorption

Food Cipro decreased elimination of caffeine

Calcium Calcium can bind quinolones

Mineral supplement Absorption of divalent cations and trivalent cations

decreased by binding to quinolones

Clarithromycin Antibiotic

(macrolide)

Food Decreased onset of absorption; no change in total

amount absorbed

Clonazepam Anticonvulsants

(benzodiazepine)

Nutrient Enhanced CNS depression

Clorazepate dipotassium Calcium Increased vitamin D requirements, owing to increased

metabolism

Vitamin D Increased bone resorption

Cyanocobalamin Decreased serum levels, leading to megaloblastic

anemia

Folic acid Decreased CSF folate and erythrocyte concentration

Serum lipis May increase cholesterol, HDL triacyclglycerols

Cloxacillin Antibiotic

(penicillin)

Food Decreased rate of absorption

Table 2 Continued

Continued

DRUG–NUTRIENT INTERACTIONS 1907

Drug Class Food/nutrient Effect/mechanism

Codeine Narcotic agonist,

analgesic

Alcohol Enhanced CNS effect

Glucose Can cause hyperglycemia

Corticosteroids Steroid Calcium,

phosphorus,

vitamin D

Decreased absorption of Ca, P; increased urinary

excretion; chronic high dose can cause osteomalacia

Dexamethazone

Hydrocortisone

Methylprednisolone

(Prednisone, Prednisolone)

Corticosteroids Steroid Nitrogen Increased urinary nitrogen losses

Zinc Increased urinary excretion and decreased serum levels

Glucose Impairs glucose tolerance; increases plasma levels

Triacylglycerols,

cholesterol

Increased serum levels

Co-trimaxazole Antibiotic Potassium Decreased excretion hyperkalemia

Sodium Increased excretion hyponatremia

Folic acid Potential for folate deficiency

Cyclosporine Antirejection Milk, fat, pineapple

juice

Increased absorption

Demeclocycline Antibiotic Food, calcium, iron Decreased absorption of dairy products and divalent and

trivalent cations

Diazepam Anticonvulsant Food Increased absorption with high-fat meals and delayed

gastric emptying

Clonazedam

Clorazepate dipotassium

Lopazepam

Oxazepam

Dicumarol Anticoagulant Food Increased absorption with high-fat meals and delayed

gastric emptying

Didanosine Tab Antiviral Food Decreased rate and extent of absorption

Oral suspension Fruit juice or acid

liquid

Didanosine unstable in acid pH

Digoxin Cardiac Food Delay absorption; adsorbent to high-fiber, high-pectin

foods

Dirithromycin Antibiotic

(macrocide)

Food Slightly increased absorption

Divalproex Anticonvulsant Food Decreased rate of absorption; extent of absorption not

affected

Doxycycline Antibiotic Food Decreased absorption of food and milk

Erythromycin Antibiotic

(macrocide)

Food Increased absorption by delayed gastric emptying

Erythromycin stearate Food Reduced absorption by delayed gastric emptying

Ethionamide Antituberculosis Pyridoxins Reports of peripheral neuritis and paresthesia

Etodolac Nonsteroidal

antiinflammatory

drug (NSAID)

Food (milk) Decreased total bioavailability of tolmetin; decreased

absorption of ibuprofen

Sodium Hyponatremia (indomethacin/ketorolac)

Potassium Hyperkalemia (indomethacin/ketorolac)

Food Increased rate of absorption

Felbamate Anticonvulsant Glucose Hypoglycemia

Magnesium Hypomagnesemia

Phosphorus Hypophosphatemia

Potassium Hypokalemia

Sodium Hyponatremia

Fenoprofen NSAID Food (milk) Decreased total bioavailability of tolmetin

Fenoprofen calcium Sodium Hyponatremia (indomethacin/ketorolac)

Potassium Hyperkalemia (indomethacin/ketorolac)

Food (milk) Decreased bioavailability of tolmetin; decreased

absorption of ibuprofen

Food Increased rate of absorption

Fluconazole Antifungal Potassium Hypokalemia

Flucytosine Antifungal Food Decreased rate of absorption; no change in extent of

absorption

Table 2 Continued

Continued

1908 DRUG–NUTRIENT INTERACTIONS

Drug Class Food/nutrient Effect/mechanism

Foscarnet Antiviral Calcium Hypocalcemia; drug chelates; divalent metal ions

Magnesium Hypomagnesemia

Phosphorus Hypo- and hyperphosphatemia

Potassium Hypokalemia

Furazolidone Antiinfective Tyramine-rich foods

(avocados,

canned figs, aged

cheese, cola

beverages,

coffee, chocolate,

wines, soy

sauces,

fermented meats,

yeast

preparation,

yogurts)

Prolonged large doses result in increased risk for

hypertensive crisis

Alcohol Flushing, headache, nausea, vomiting, sweating,

tachycardia

Furosemide Diuretic Food Delayed absorption

Ganciclovir Antiviral Food Increased area under curve plasma concentration

Glipizide Antidiabetic Food Delayed absorption

Alcohol Flushing, headache, nausea, vomiting, sweating,

tachycardia

Sodium Hyponatremia, SIADH

Griseofluvin Antifungal Alcohol Can increase alcohol effect, flushing, tachycardia

High-fat food Increased drug absorption rate

Hydralazine Diuretic Food Increased absorption

Hydrochlorothiazide Diuretic Food Increased absorption by delayed gastric emptying

Ibuprofen NSAID Food (milk) Decreased total bioavailability of tolmetin; decreased

absorption of ibuprofen

Sodium Hyponatremia (indomethacin/ketorolac)

Potassium Hyperkalemia (indomethacin/ketorolac)

Food Increased rate of absorption

Indinavir Antiviral Food Decreased absorption of high-calorie, high-fat, and

protein

Grapefruit juice Decreased area under curve concentration

Indomethicin NSAID Food (milk) Decreased total bioavailability of tolmetin; decreased

absorption of ibuprofen

Sodium Hyponatremia (indomethacin/ketorolac)

Potassium Hyperkalemia (indomethacin/ketorolac)

Food Increased rate of absorption

Iron Mineral Ascorbic acid Increased absorption

Amino acids Increased absorption

Calcium phosphate Decreased absorption

Zinc Inhibits absorption

Vitamin A Vitamin A deficiency inhibits iron utilization and

accelerates development of anemia

Tea/coffee Decreased absorption owing to formation of iron tannate

Vegetable

polyphenols

Binds and insolubilizes iron

Isoniazid Antituberculosis Food Decreased intestinal absorption

Pyridoxine Decreased metabolism, antagonism

Food and histamine,

tuna, liver,

aubergine,

parmesan

cheese, tomato,

spinach,

tyramine-

containing foods

Headache, redness, itching of eyes and face, chills,

diarrhea, palpitation

Potential hypertensive crisis owing to monoamine

oxidase inhibitor activity

Table 2 Continued

Continued

DRUG–NUTRIENT INTERACTIONS 1909

Drug Class Food/nutrient Effect/mechanism

Itraconazole Antifungal Food Increased absorption, increased triacylglycerols

Potassium Hypokalemia

Ketoconazole Antifungal Alcohol Flushing, headache, nausea, vomiting, sweating,

tachycardia

Labetalol Antihypertensive Food Increased absorption

Lamivudone (3TC) Antiviral Food Decreased rate of absorption

Levodopa Anti-Parkinson Food Decreased absorption; with high-protein meals amino

acids compete for absorption

Lithium Antimanic Low-sodium diet Increased lithium concentrations

High-sodium diet Increased lithium clearance

Food Increased absorption

Lomefloxacin Antibiotic

(quinolone)

Food Decreased rate and extent of absorption

Loracarbef Antibiotic Food Increased rate of absorption

Lovastatin Antihyperlipidemia Food Increased absorption

Mebendazole Anthelmintic Food Increased absorption

Meclofenamate NSAID Alcohol Additive CNS effects; increased prothrombin time

Food Decreased bioavailability

Melphalan Antineoplastic Food Reduced absorption

Mercaptopurine Antineoplastic Food Reduced absorption

Methacycline Antibiotic Food, calcium, iron Decreased absorption of dairy products, cereals,

divalent and trivalent cations

Methenamine mandelate Urinary antiinfective Milk products, citrus

fruits

Excessive amounts inhibits drug conversion

Methosuximide Anticonvulsant Alcohol, calcium Additive CNS effects; hypocalcemia

Methotreate Antineoplastic Food Increased absorption

Methyldopa Antihypertensive Vitamin B

, folate In high doses methyldopa can increase vitamin B

and

folate losses

Food High-protein meals compete for absorption

Metoprolol Antihypertensive Food Increased absorption

Metronidazole Antibiotic Alcohol Flushing, headache, nausea, vomiting, sweating,

tachycardia

Food Decreased peak serum concentration but total amount of

drug absorbed not affected

Minocycline Antibiotic Food, calcium Decreased absorption

Nafcillin Antibiotic Food Decreased absorption; decreased serum levels owing to

altered gastric pH

Potassium High doses can cause hypokalemia owing to increased

urinary losses

Nifedepine Antihypertensive

calcium channel

blocker

Grapefruit juice Increased serum level of nifedepine flavonoids inhibits

cytochrome P-450

Food Decreased bioavailability, formulation dependent

Nitrofurantoin Antibiotic Food Increased absorption by delayed gastric emptying

NSAIDs NSAID Food (milk) Decreased bioavailability of tolmetin

Diclofenal Sodium Hyponatremia (indomethacin/ketorolac)

Etodolac

Fenoprofen Ca Potassium Hyperkalemia (indomethacin/ketorolac)

Ibuprofen

Ketoprofen Food Decreased absorption of ibuprofen

Ketorolac

Naproxen

Oxaproxin

Piroxican

Sulindac

Tolmetin NA Food Increased rate of absorption

Norfloxacin Antibiotic

(quinolone)

Food, dairy products Decreased rate of absorption

Multivitamin and

mineral

supplements

Decreased absorption owing to formation of divalent/

trivalent cation complexes with quinolones

Oflaxacine Antibiotic

(quinolone)

Dairy products and

mineral

supplements

Decreased absorption by polyvalent cations

Table 2 Continued

Continued

1910 DRUG–NUTRIENT INTERACTIONS

Drug Class Food/nutrient Effect/mechanism

Ondansetron Antiemetic Food Increased extent of absorption

Potassium Hypokalemia

Oral contraceptives Ascorbic acid Decreased ascorbic acid concentration in plasma,

platelets, leucocytes

Vitamin C, folic acid Decrease in their serum levels

Vitamin B

Impairs tryptophan metabolism

Amino acids,

vitamin A, vitamin

E, copper

Increase in their serum levels

Oxacillin Antibiotic Food Decreased absorption and decreased serum

concentration

Fats Oxacillin can cause steatorrhea

Paromomycin Amoebicide Food Increased absorption by delayed gastric emptying

Vitamins A, D, E, K Malabsorption of fat-soluble vitamins owing to

hypocholesterolemia

Penicillamine Antidote (chelating

agent)

Food Decreased absorption

Iron/zinc Decreased absorption 30–70% of increased zinc

absorption; decreased penicillamine absorption

Penicillin G & VK Antibiotic Food Decreased absorption by delayed gastric emptying

Glucose Hyperglycemia

Pentamidine Antibiotic Calcium,

magnesium

Hypomagmanesemia, hypocalemia

Potassium Hyperkalemia due to nephrotoxicity

Phenacemide Anticonvulsant Fresh fruits and

vitamin C

Increased urinary excretion of phenacemide

Phenobarbital Anticonvulsant (see

Barbiturates)

Food Decreased absorption owing to protein binding

Protein Low-protein diet increases duration of action of

phenobarbitol

Vitamin D, calcium Decreased serum vitamin D by cytochrome P-450

hypocalcemia

Fresh fruits and

vitamin C

Increased urinary excretion of phenobarbitol

Phensuximide Anticonvulsant

(succinimides)

Calcium, vitamin D Decreased serum vitamin D by P-450 cytochrome

hypocalcemia

Vitamin B

, folic

acid

Decreased absorption and serum levels of folates;

inhibits vitamin B

transport

Copper Increased serum levels

Phenytoin Anticonvulsant

(hydantoins)

Fresh fruits and

vitamin C

Increased urinary excretion

Vitamin D, calcium Decreased serum vitamin D by cytochrome P-450

hypocalcemia

Enteral feeds Decreased absorption

Food Increased absorption by delayed gastric emptying

Piroxicam Food Delayed absorption

Praziquantel Anthelmintic Food Decreased rate and extent of absorption

Primidone Anticonvulsant Fresh fruits and

vitamin C

Increased urinary excretion of primidone

Protein Low-protein diet increases duration of action of

primidone

Propranolol Antihypertensive High-protein foods Increased absorption

Propantheline Food Decreased absorption

Proxyphene Analgesic Food Increased absorption by delayed gastric emptying

Pyrimethamine Antimalarial Folic acid Decreased serum folate concentrations

Quinidine Antiarrhythmic Food Delayed absorption owing to protein binding

Riboflavin Vitamin Food Increased absorption by delayed gastric emptying

Rifampin Antibiotic Food Decreased absorption

Ritonavir Antiviral Vitamins Can cause vitamin deficiency

Potassium Hyper- and hypokalemia

Cholesterol Hypercholesterolemia

Triacylglycerols Hypertriacylglycerolemia

Food Delayed absorption

Oral solution capsules Food Increased extent of absorption

Table 2 Continued

Continued

DRUG–NUTRIENT INTERACTIONS 1911

into the brain by the same transport system as the

large neutral amino acids, and thus must compete

with them for use of the carrier binding sites. Diet

composition, by affecting the postprandial amino

acid profile, may change significantly the clinical effi-

cacy of drugs such as l-dopa, used in the treatment of

Parkinson’s disease.

0018 Body composition is also a relevant determinant of

drug disposition and action. Although most drug

dosages are calculated by total body weight, most

drugs only act in the fat-free body mass. Thus, at a

given body weight, individuals with more body fat

will tend to receive a higher effective dose than those

with lower body fat. The size of the body fat mass is

also important for drugs that are stored in adipose

tissue.

Major Drug–Nutrient Interactions of

Clinical Relevance

0019Table 2 provides information on the major drug–

nutrient interactions of clinical relevance. The list

reflects well-known interactions of drugs that have

been in the market for some time. The US Food and

Drug Administration (FDA) maintains an on-line

database of recently reported interactions and

those of new drugs. The database can be assessed at

www.fda.gov.

Drug Class Food/nutrient Effect/mechanism

Salicylates Analgesic Iron Long-term chronic use decreases serum iron

Magnesium salicylate

Choline salicylate Vitamin C Decreases concentration in serum and platelets

Sodium salicylate Amino acids Decreases their intestinal absorption and increases

urinary secretion

Saquinavir mesylate Antiviral Food Increased absorption of high-calorie, high-fat foods

Calcium Hypercalemia

Glucose Hyper- and hypoglycemia

Phosphorus Changes in serum phosphorus

Potassium Hyper- and hypokalemia

Spironolactone Diuretic Food Increased absorption by delayed gastric emptying

Sulfonamides Antibiotic Food Delayed with no effect on extent of absorption

Sulfdiazine

Sulfisoxazole Folic acid Decreased intestinal synthesis, absorption and serum

levels

Sulfamethoxazole

Te t r a c y c lin e Antibiotic Food Decreased absorption

Minerals Inhibits absorption of iron, calcium, zinc and

magnesium; chelation by polyvalent cations

Fats Decreases their absorption

Vitamin K Decreases bioavailability

Vitamin C Increase urinary losses; decreases plasma and

leucocytes and levels

Theophylline Broncodilator Charbroiled beef Increased metabolism of theophylline

High-fat meals Increased absorption dependent on formulation

Tola z a mid e Antidiabetic Sodium Hyponatremia and SIADH

Tolb u t amid e

Trimethoprim Antibiotic Folic acid Decreased serum folate levels

Valproic acid Anticonvulsant Milk, food,

carbonated drinks

Delayed absorption but no effect on extent of absorption

Divalproex sodium

Valproate sodium

Oral solution

Warfarin Anticoagulant Alcohol Inhibits warfarin metabolism

Vitamin K Beef liver, pork liver, green tea, leafy green vegetables

high in vitamin K inhibit anticoagulant effect

Vitamin E Can increase warfarin response

Zalcitabine Antiviral Food Decreased rate and extent of absorption

Zidovudine Antiviral Food Decreased rate of absorption

CSF, cerebrospinal fluid; NSAID, nonsteroidal antiinflammatory drug; SIADH, Syndrome of Inappropriate Antidiuretic Hormone excretion.

Table 2 Continued

1912 DRUG–NUTRIENT INTERACTIONS

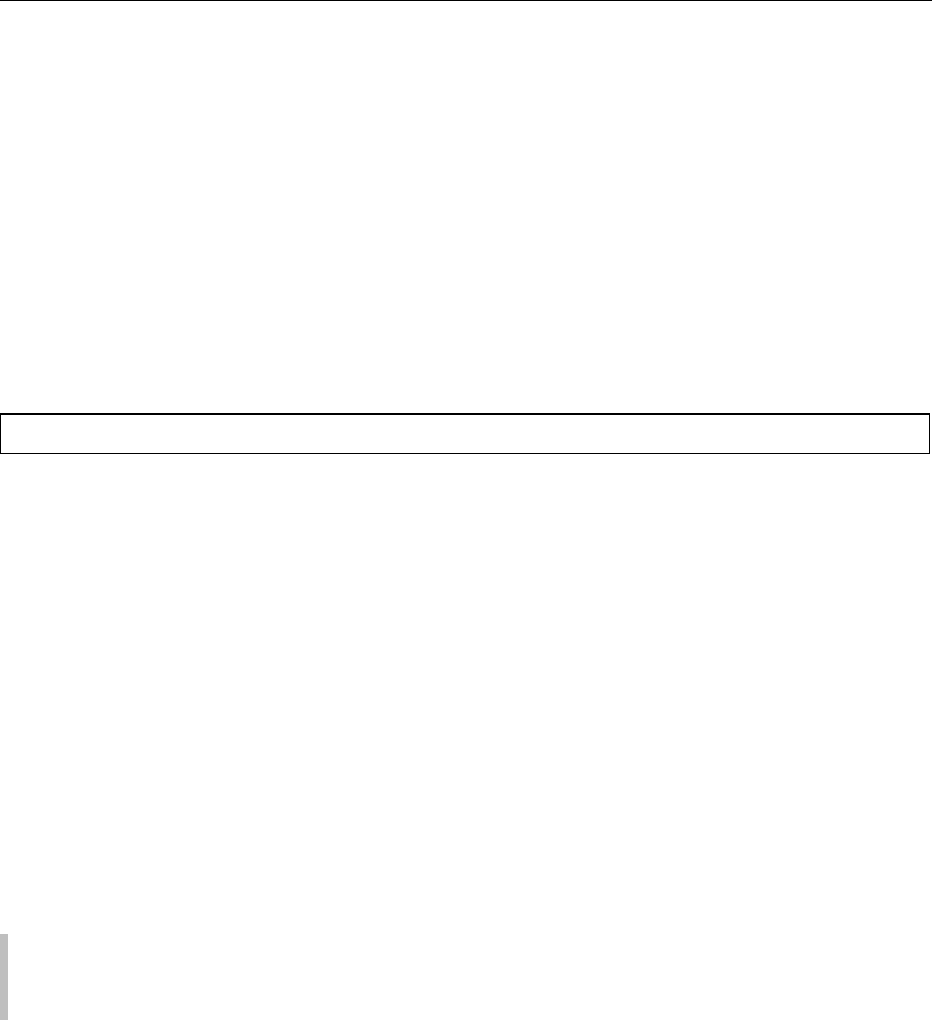
See also: Amino Acids: Metabolism; Malnutrition: The

Problem of Malnutrition; Malnutrition in Developed

Countries

Further Reading

Caballero B (1988) Nutritional implications of dietary

interactions: a review. Food Nutrition Bulletin 10: 9–20.

Knapp HR (1996) Nutrient–drug interactions. In: Ziegler

FF and Filer LJ (eds) Present Knowledge in Nutrition,

pp. 540–546. Washington, DC: ILSI Press.

Neuvonen P (1989) Clinical significance of food–drug inter-

actions. Medical Journal of Australia 150: 36–40.

Roberts J (1988) Age and diet effects on drug action.

Pharmacology and Therapeutics 37: 111–149.

Roe DA (1986) Drug food and drug nutrient interactions.

Journal of Environmental Pathology, Toxicology and

Oncology 5: 115–135.

Roe DA (1994) Diet, nutrition and drug reactions. In: Shils

ME, Olson JA and Shike M (eds) Modern Nutrition in

Health and Disease, 8th edn, pp. 1399–1416. Phila-

delphia, PA: Lea & Febiger.

Wurtman RJ, Caballero B and Salzman E (1988) Facili-

tation of DOPA-induced dyskinesias by dietary carbo-

hydrates. New England Journal of Medicine 390:

1288–1289.

Drugs See Antibiotics and Drugs: Uses in Food Production; Residue Determination

DRYING

Contents

Theory of Air-drying

Drying Using Natural Radiation

Fluidized-bed Drying

Spray Drying

Dielectric and Osmotic Drying

Physical and Structural Changes

Chemical Changes

Hygiene

Equipment Used in Drying Foods

Theory of Air-drying

J G Brennan, The University of Reading, Reading, UK

Background

0001 Drying, or dehydration, is the oldest method of food

preservation practiced by man, and today it is a major

contributor to the convenience food market. The main

objective of drying food is to prolong its shelf-life

beyond that of the fresh material, while at the same

time minimizing undesirable changes in appearance,

texture, flavor, and nutritional value during the drying

process. In addition to the preservation of the product,

drying can bring about savings in storage and

transport of foods owing to the reduction in weight

and bulk that occurs during most methods of drying.

Water in Foods

0002Water is an important contributor to the sensory qual-

ity of foods and a loss or gain of moisture from a

product can adversely affect its acceptability. However,

a certain amount of moisture in foods enables undesir-

able changes to occur as a result of the activity of

microorganisms and enzymes or through nonenzymic

chemical reactions. (See Drying: Chemical Changes.)

Thus, removing moisture from a food, or making it less

available, is one way of extending its shelf-life.

0003The moisture content of a wet material may be

expressed on a wet-weight basis (wwb), i.e., the mass

of water per unit mass of the wet material, or on a

DRYING/Theory of Air-drying 1913

dry-weight basis (dwb), i.e., the mass of water per unit

mass of dry solids. The latter way of expressing mois-

ture content is usually used in drying formulae and

calculations; see section Theory of Air Drying.

0004 However, when the influence of moisture on the

stability of foods is being studied, it is not only

the total moisture content that is of importance but

also how much of that moisture is available to sup-

port the activity of microorganisms and enzymes and

enable chemical changes to occur. It is now widely

accepted that a fraction of the total moisture in food

is strongly bound to individual sites on the solid

components and is not available to support these

activities. An additional amount of moisture is less

firmly bound but is still not readily available as a

solvent for soluble components of the food. Such

‘bound’ moisture exerts a vapor pressure less than

the vapor pressure of pure water at the prevailing

temperature. A property known as water activity

) is used to represent the availability of moisture

in foods thus:

ð1Þ

where p

is the water vapor pressure exerted by a

solution or wet solid, and p

is the vapor pressure

of pure water at the same temperature. This

expression also represents the relative humidity of

an air–water vapor mixture ( 100 to give the per-

centage relative humidity). A graph of moisture con-

tent as a function of water activity, with which it is in

equilibrium, is known as a sorption isotherm.Such

plots may be constructed by adsorption or desorp-

tion, which, in the case of many foods, results in two

different curves, exhibiting hysterisis (Figure 1). Food

isotherms may be considered to be made up of three

regions. In region A, water is strongly bound to spe-

cific sites on the solid components, is not available as

a solvent, and so does not support, microbiological,

enzymic or chemical activity. The amount of moisture

held in this way is known as the monolayer or mono-

molecular moisture content. This type of moisture

usually exits below a

0.35, corresponding to a mois-

ture content range 0.05–0.11 (dwb). Above region A,

water is less strongly bound to the solids but still does

not exert its full vapor pressure. In some publications,

region B (Figure 1), is said to contain moisture that is

bound in multilayers to the solid, and in region C,

structural and solution effects lower the water vapor

pressure. However, it is more likely that all these

effects have an influence over the whole isotherm.

At moisture contents of 1.0 (dwb) and above, most

foods exert vapor pressures equal to that of pure

water. Temperature affects the sorption behavior of

foods according to the expression:

d ðlna



¼

, ð2Þ

where T is the absolute temperature, Q

is the heat of

adsorption, and R is the gas constant. The amount

of adsorbed water at any given value of a

decreases

as the temperature increases.

0005Numerous mathematical models have been proposed

to represent sorption isotherms of foods. One of the

earliest was the Brunauer–Emmet–Teller isotherm:

ð1a

ÞW

ðC  1Þ

, ð3Þ

where W is the total moisture content (dwb), W

the monolayer moisture content (dwb), and C is con-

stant. This model is said to apply over the a

range

0.05–0.45. An extended version of eqn (3), which

takes into account multilayer adsorption and is said

to be applicable up to a

0.90, is the Guggenheim–

Anderson–DeBoer model:

Cka

ð1  ka

Þð1  ka

þ Cka

, ð4Þ

where C is known as the ‘Guggenheim’ constant, and

k is a factor correcting properties of the multilayer

molecules with respect to the bulk liquid.

0006A knowledge of the sorption characteristics of

foods is useful in the prediction of drying times and

energy requirements for drying processes. When

0 0.2 0.4

Desorption

Adsorption

Moisture content

0.6

Water activity

0.8 1.0

fig0001Figure 1 Adsorption and desorption isotherms showing hys-

teresis. From Brennan JG, Butters JR, Cowell ND and Lilly AEV

(1990) Food Engineering Operations, 3rd edn. London: Elsevier

Applied Science, with permission.

1914 DRYING/Theory of Air-drying

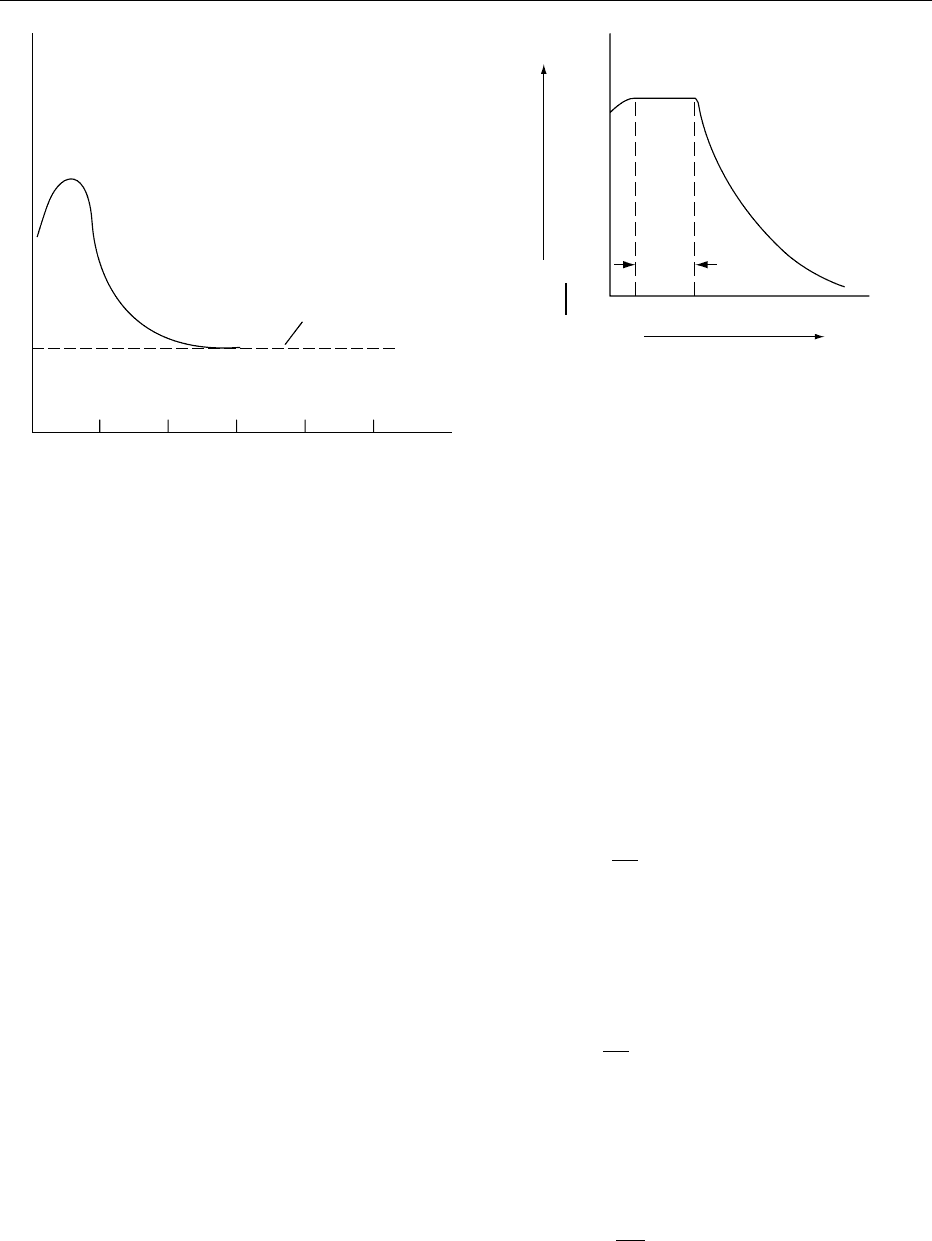
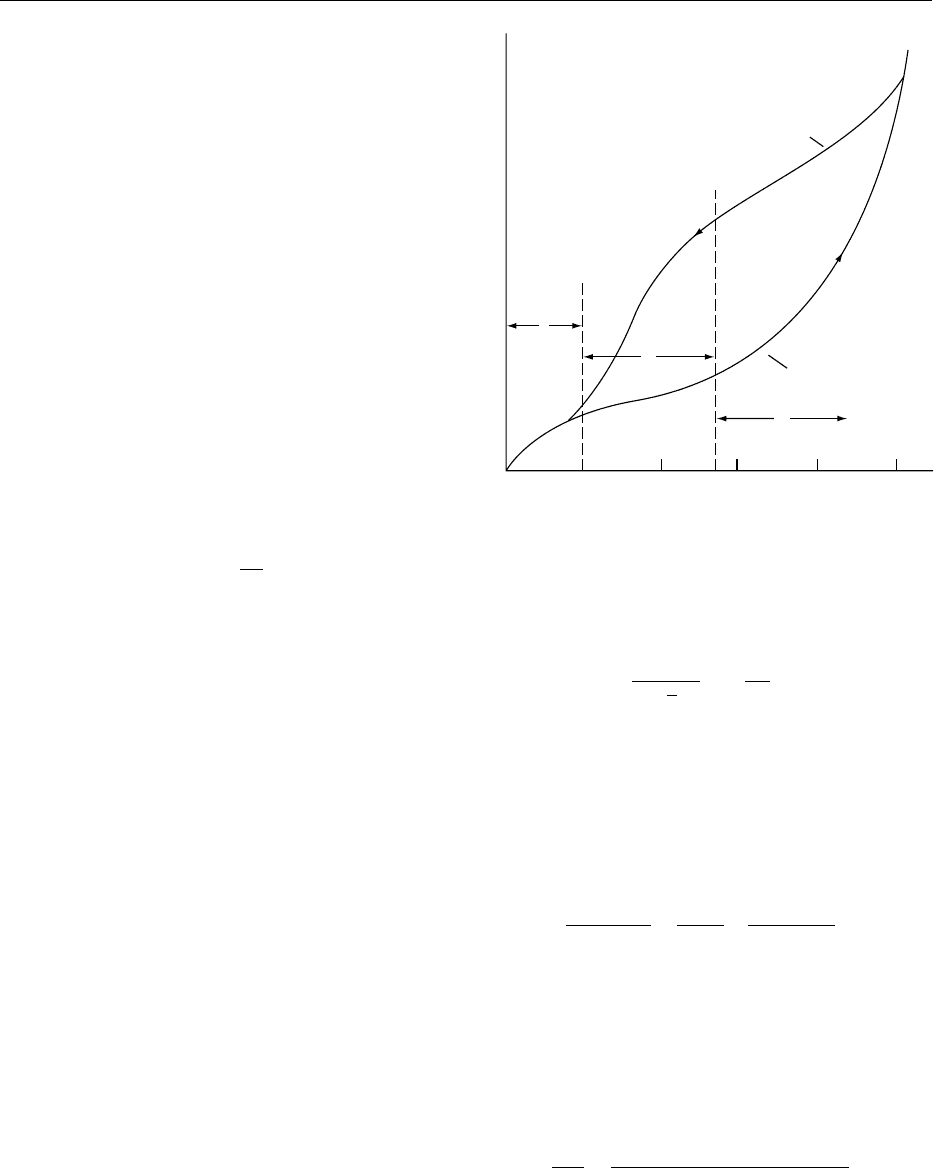
drying to very low moisture contents, extra energy is

required to overcome the bonding of the water to the

solids (Figure 2). The influence of a

on the stability

and shelf-life of foods is covered in Drying: Chemical

Changes. The most common method of drying foods

is air drying.

Theory of Air Drying

0007 When a wet material is placed in a current of heated

air, the air performs two main functions: it supplies

the sensible and latent heat to bring about the evap-

oration of the moisture, and it acts as a carrier to

move the water vapor formed away from the drying

surface, thus enabling further evaporation to take

place. Consider a wet solid composed of pure water

and inert solids, in the form of a thin slab, which is

placed in a current of heated air. If it is assumed that

drying takes place from one large face only, that the

temperature, humidity, and velocity of the air remain

constant, and that all the heat is transferred from the

air by convection, the drying curve should have the

familiar shape shown in Figure 3. It comprises a

number of stages or periods.

000 8 Period A–Bisanequilibration period during which

equilibrium is attained between the wet solid and the

drying air. This period usually takes up a relatively

small part of the drying curve.

000 9 Period B–C is known as the constant rate period,as

the rate of drying remains constant during the period.

Throughout this period, the surface of the solid is

fully saturated with water. The movement of water

from within the solid is sufficient to maintain satur-

ated conditions at the surface. A state of equilibrium

exists at the surface as the heat transfer to the surface

from the air balances the rate of evaporation from

the surface. The temperature at the surface of the

solid remains constant at a value that corresponds to

the wet-bulb temperature of the air. The driving

force that causes water to evaporate into the air is

the difference in water vapor pressure at the surface

from that in the main air stream. The rate of drying,

i.e., rate of change of weight (dw/dt), may be repre-

sented by the expression:

¼K

Aðp

 p

Þ, ð5Þ

where K

is the mass transfer coefficient, A is

the drying area, p

is the water vapor pressure at the

surface of the solid, and p

is the water vapor pressure

in the main stream of the air. Eqn (5) may also

be written as:

¼K

AðH

 H

Þ, ð6Þ

where K

is the mass transfer coefficient, H

is the

absolute humidity at the surface of the solid, and H

is the absolute humidity in the main air stream.

0010The rate of heat transfer from the air to the drying

surface (dQ/dt) may be represented by the expression:

¼ h

Að#

 #

Þ, ð7Þ

where h

is the convection heat transfer coefficient, #

is the dry-bulb temperature of the air, and #

is the

wet-bulb temperature of the air (temperature at

0 0.2 0.4

Water activity

Latent heat of vaporization

for water

Total heat adsorption (Arbitrary units)

0.6 0.8 1.0

fig0002 Figure 2 Dependence of the total heat of adsorption (latent

heat plus heat of adsorption) on water activity. Adapted from

Karel M (1974) Fundamentals of drying processes. In: Spicer A

(ed.) Advances in Pre-concentration and Dehydration of Foods,

pp. 45–94. London: Applied Science.

t−(h)

− kg/(kg dry solids)(h)

fig0003Figure 3 Model drying curve for a slab-shaped wet solid in air

at constant temperature, humidity, and velocity. Adapted from

Brennan JG, Butters JR, Cowell ND and Lilly AEV (1990) Food

Engineering Operations, 3rd edn. London: Elsevier Applied Sci-

ence, with permission.

DRYING/Theory of Air-drying 1915