Buschow K.H.J. (Ed.) Concise Encyclopedia of Magnetic and Superconducting Materials

Подождите немного. Документ загружается.

(eds.) Ferromagnetic Materials. Elsevier, Amsterdam, Vol. 5,

pp. 238–322

Wassermann E F, Acet M, Entel P, Pepperhoff W 1999 Basic

understanding of the relations between Invar, anti-Invar and

martensite in Fe-based alloys. J. Magn. Soc. Jpn. 23, 385–90

Weiss R J 1963 The origin of the Invar effect. Proc. Phys. Soc.

London 82, 281–8

Wittenauer J (ed.) 1997 The Invar Effect: A Centennial Sym-

posium. Mineral, Metals and Materials Society, Warrendale,

PA, pp. 51–62

E. F. Wassermann

Gerhard-Mercator-Universita

t, Duisburg, Germany

Itinerant Electron Systems: Magnetism

(Ferromagnetism)

The development of the electron band model (Bloch

1929) paved the way for an understanding of the

magnetism of ‘‘itinerant’’ electrons. The ﬁrst attempts

to understand the metallic state were based on the

free electron gas model and Pauli (1927) showed that

the quenching of the spin can be explained if it is

assumed that all the electrons in open shells (con-

duction electrons) are at least partially free. The Pauli

exclusion principle requires that two electrons have to

be different in at least one quantum number. For free

electrons the only relevant quantum numbers are the

spin and the electron momentum k. Since any state

with quantum number k can accommodate two elec-

trons, these electrons must have opposite spin so that

all spins appear to be compensated. For the suscep-

tibility of the noninteracting (no exchange) gas of free

electrons Pauli developed his well-known expression:

¼ 2m

Nðe

Þð1Þ

which relates the paramagnetism of the free electrons

to the density of states at the Fermi energy N(e

Formally this relation resembles the result for the

specific heat of the free electron gas which also de-

pends on the density of states at the Fermi energy.

These ideas about the metallic state described as an

electron gas were further developed by Mott (1935)

and Slater (1936a, 1936b), who introduced more re-

alistic models for the bandstructure and ﬁnally by

Stoner (1936, 1938), who succeeded to formulate a

phenomenological ‘‘molecular ﬁeld’’ model (analo-

gous to the Weiss model) by employing the electronic

bandstructure instead of the discrete angular mo-

mentum levels. This model of itinerant electron mag-

netism accounts for noninteger magnetic moments in

terms of a band ﬁlling of the narrow d band and by

taking into account the interaction of the s and d

electrons of the valence band. Within the frame-

work of the Stoner model, the susceptibility of the

interacting (including exchange) gas of free electrons

becomes enhanced by the exchange interaction and

reads:

Nðe

1  INðe

ð2Þ

The quantity I in Eqn. (2) is the Stoner exchange

factor, which is a slowly varying atomic quantity

through the periodic table. The denominator allows

the formulation of a criterion for the spontaneous

onset of magnetism. If, in the nonmagnetic state the

denominator is negative, the resulting negative sus-

ceptibility means that the paramagnetic state is not at

a total energy minimum but at a maximum, so that

any magnetic state must have a lower total energy.

This is the famous Stoner criterion which is usually

formulated such, that magnetism occurs if the in-

equality holds:

INðe

ÞX1 ð3Þ

An attempt to clarify the role of the exchange in-

teraction in metals was made by performing Hartree–

Fock calculations for the free electron gas in com-

parison to tight binding calculations for the valence

electrons (see review by Wohlfarth (1953)).

A crucial step towards the understanding and

practicability of quantum mechanical calculations

of the metallic state was done by Slater (1951). He

suggested that the exchange interaction could be

approximated by an averaged potential over the

occupied states of a homogenous electron gas, which

is no longer a nonlocal quantity but depends only on

the local electron density at the point r:

ðrÞ¼3e



1=3

rðrÞ

1=3

ð4Þ

A significant improvement to the Slater exchange

occurred with the introduction of the Xa method

where the Slater exchange potential v

(r) is multiplied

by a factor a, which is determined from the require-

ment that the total energy of an isolated atom cal-

culated from the Xa-potential equals the respective

Hartree–Fock value (Schwarz 1972).

The next major step towards an understanding of

the electronic structure of solids and subsequently of

their magnetism was the density functional formalism

introduced by Hohenberg and Kohn (1964). They

showed that the ground state energy can be expressed

in terms of a universal functional of the electron

density (for details on this subject area see Density

Functional Theory: Magnetism). The variation of the

energy with respect to the electron density leads to

effective one-electron Schro

dinger type equations

(Kohn and Sham 1965). In these equations the ex-

change-correlation potential v

(r) enters additively

to the Coulomb part, allowing straightforward use of

independent interpolation formulae to approximate

340

Itinerant Electron Systems: Magnetism (Ferromagnetism)

(r). This treatment is called the ‘‘local spin density

approximation’’ (LSDA) for exchange and correla-

tion (Hedin and Lundquist 1971, von Barth and

Hedin 1972, Parr and Yang 1989).

Table 1 compares the values for DE and I for h.c.p.

(f.c.c.) cobalt for some commonly used models of the

LSDA. Table 1 shows that most of the usual models

yield too large a band splitting and Stoner factor.

This shortcoming is due to an incomplete description

of correlation effects. Only in case (c), where a special

treatment is used to improve the correlation, do the

calculated values come closer to the experimental es-

timates. Despite the large scattering found for DE

and I the calculated magnetic moments are all be-

tween 1.55 and 1.7 m

(exp: 1.62 m

). The data given

in Table 1 are taken from: (a) best value from exper-

iments (h.c.p. cobalt) given by Wohlfarth (1980), (b)

Xa result for f.c.c. cobalt given by Wakoh and Yam-

ashita (1970), (c) to obtain an improved description

of the correlation effects Oles and Stollhoff (1986)

introduced their local approach (LA) (f.c.c. cobalt),

and (d) and (e) are values taken from Mohn and

Schwarz (1993) for h.c.p. cobalt employing the

Hedin–Lundquist (HL) and the von Barth–Hedin

(vBH) exchange potential.

Parallel to the development of bandstructure the-

ory there was a search for ‘‘simple’’ toy models to

explain solid state magnetism. The most prominent of

these models was introduced by Hubbard (1963),

who tried to describe transition metal oxides with

their narrow d bands and their strong correlation.

These models resemble the main features of electrons

in a solid which are the bonding to a certain site and

the Coulomb repulsion of electrons at the same site.

With these tools at hand it became possible to cal-

culate the ground state properties with high reliability

and also to understand the complex mechanisms

occurring in solids. Among the remaining problems

the most crucial one was the temperature dependence

of solid state magnetism. While for the localized

moment models the ﬁnite temperature effects became

reasonably clear at a very early stage, this develop-

ment took some time for metals.

For the free electron gas the temperature depend-

ence of the susceptibility was calculated from the

ﬁnite temperature properties of the Fermi–Dirac dis-

tribution (Sommerfeld expansion). Stoner applied the

same ideas to introduce ﬁnite temperatures into the

itinerant electron model. Unfortunately, the respec-

tive Curie temperatures T

came out too large by a

factor of 4–8 and the inverse susceptibility above T

showed a T

rather than a linear T dependence (as

observed experimentally). After years of persistent

struggle to salvage the ﬁnite temperature Stoner

model, it ﬁnally became clear that the single particle

excitations are not (or only to a small amount)

responsible for the ﬁnite temperature behavior of

metallic magnetism.

These results suggest that two extreme limits must

be considered:

(i) the localized limit for which the magnetic mo-

ments and their ﬂuctuations are localized in space

(delocalized in k space), with their amplitudes being

large and ﬁxed.

(ii) the itinerant (or weak ferromagnetic) limit for

which the moments and their ﬂuctuations are local-

ized in k space (delocalized in real space), with their

amplitudes being temperature dependent.

A Curie–Weiss law is observed in both cases but its

physical origin and the corresponding value of the

Curie constant is different.

To solve these inconsistencies, Moriya and Kawa-

bata (1973) tried to include thermally induced collec-

tive excitations of the spins (as they were already

known for localized spins) in order to formulate an

uniﬁed picture of magnetism (for a review see Moriya

1985). A similar approach was introduced by Murata

and Doniach (1972), who introduced local and ran-

dom classical ﬂuctuations of the spin density (spin

ﬂuctuations) which should be excited thermally. Both

of the latter two models become equivalent at high

temperatures and lead to a Curie–Weiss law. Although

the Murata–Doniach approach runs into trouble at

T ¼0 K (the classical ﬂuctuations violate of the third

law of thermodynamics), it has successfully been

applied to calculate T

from data derived from de

Haas–van Alphen measurements (Lonzarich and Tail-

lefer 1985) and to formulate a simple model for T

metallic solids (Mohn and Wohlfarth 1986) which

gives much better results than the Stoner model.

1. Models for Delocalized Moments

The magnetism of the delocalized (itinerant) band

electrons represents an extreme limit of solid state

magnetism. For these electrons the angular quantum

number is no longer a sufﬁcient description of their

quantum state since their properties are described by

a new quantum number, the electron momentum k.

Together with the symmetry breaking due to the

crystal ﬁeld, it is also this quantum number which is

responsible for the quenching of the angular momen-

tum. Each electronic state, which is now represented

by a certain value of k, is occupied with elec-

trons which differ pairwise in all their other quantum

Table 1

Exchange splitting DE and Stoner factor I for closed

packed cobalt for various models of the LSDA for

exchange and correlation.

exp

vBH

DE (eV) 1.05 2.05 1.23 1.40 1.49

I (eV/m

) 0.65 1.21 0.72 0.93 0.96

a–e See text for details.

Itinerant Electron Systems: Magnetism (Ferromagnetism)

341

numbers so that the total angular momenta are always

close to zero. In this situation the discrete energy lev-

els, which were characterized by their magnetic quan-

tum number m

and integer occupation numbers,

which appeared in the Weiss model, have now to be

replaced by quasi-continuous energy levels. These are

characterized by the respective k vector and a no

longer integer occupation number given by the density

of states. Since the electron states are given by plane

waves (Bloch states) they extend over the whole crys-

tal. A possible magnetic moment created by these

electrons is no longer localized at a certain atomic site

but appears to be smeared out (delocalized) over the

whole crystal. In the limit of the free electron gas the

electron density is constant in real space, so that a

magnetic moment (which would better be described by

the spin density) is also constant everywhere in space.

The magnetic behavior of the delocalized electrons

can be described by transforming the real-space

properties of the localized moments into k space.

The delocalized electrons are localized in k space, the

intra-atomic exchange interaction (localized in real

space), which was responsible for the formation of a

localized moment, is now an interatomic-like ex-

change interaction localized in k space. Also the en-

ergetic localization of the atomic-like energy states is

now broadened to a band state and appears to be

energetically delocalized.

This extreme point of view is of course only valid

for a quasi-free electron description of metallic solids.

If a metal can be described by considering a quasi-free

electron behavior only, its paramagnetic susceptibility

should be given by the Pauli susceptibility (Eqn. (1)).

However, even for simple metals like the alkalines the

Pauli values are too low compared to experimental

values. The reason for this discrepancy is the relatively

high electron density in solids (even in simple metals

such as sodium) which leads to a non-negligible ex-

change interaction (c.f. Eqn. (4)). In extreme cases like

f.c.c. palladium, the Pauli susceptibility is too low by

a factor of 9–10. Although d electron systems like

palladium (but also iron, cobalt, and nickel) are far

from showing a ‘‘free electron-like’’ behavior, since

the d electron band width is much smaller than that of

the s band, their magnetism can be described along

similar lines. This is due to the fact that for a fermion

system all excitations (either thermally or due to an

external ﬁeld) occur in a narrow energy range around

the Fermi surface so that only the properties at the

Fermi energy are relevant.

1.1 The Stoner Model of Itinerant Electron

Magnetism

Stoner (1936, 1938) formulated his model of itine-

rant electron magnetism which can be seen as a

transcription of the Weiss model for metallic solids.

Stoner replaced the local ‘‘free atom-like’’ energy

levels in the Weiss model, which are characterized by

their respective magnetic quantum number, by the

electronic bandstructure. Due to the crystal ﬁeld in-

teraction in solids the angular momentum appears to

be quenched (angular quantum numbers are no long-

er relevant), so that only the k vector and the spin of

the valence electrons remains in describing the state

of the electrons. The model is based on the following

three postulates: (i) the carriers of magnetism are the

electrons in the d band, (ii) effects of exchange and

correlation are treated within a molecular ﬁeld term,

and (iii) it must conform to Fermi statistics.

It is assumed that for an applied magnetic ﬁeld,

which is the molecular ﬁeld (eventually including an

external ﬁeld H

) the Fermi energy of the paramag-

netic state is shifted to new values e

for spin-up and



for spin-down which leads to new occupation

numbers n

and n



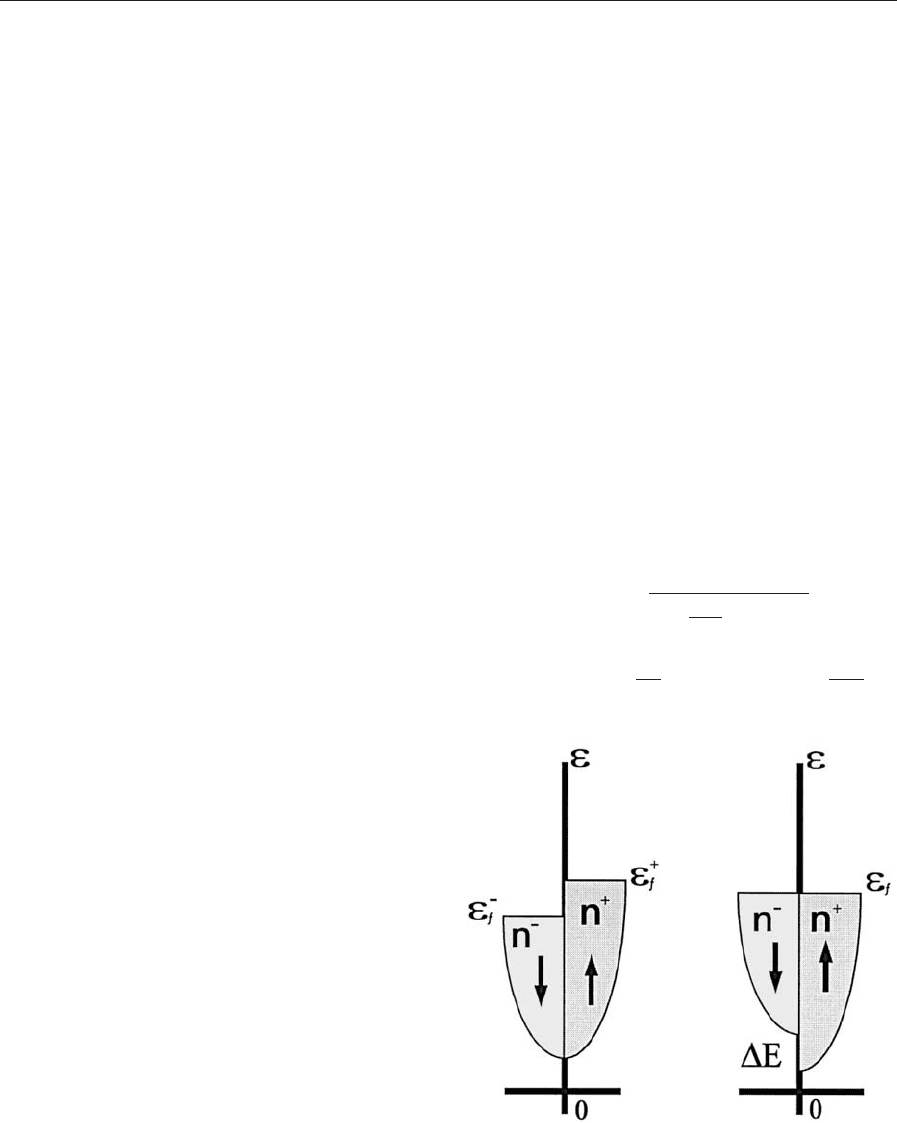
(Fig. 1, left panel). This picture is

identical to the actual shifting of the two spin-

dependent bands by the spin splitting DE (Fig. 1,

right panel).

Since the Fermi energy is the energy of the highest

occupied state it is equal to the chemical potential m;

and consequently the new Fermi energies, caused by

the ﬁeld, can be seen as chemical potentials for spin-

up ( þ) and spin-down ()asm

and m



. The Stoner

equations can now be formulated:

NðeÞ

exp

 Z



þ 1

de ð5Þ

¼ k

TZ7

with Z ¼

Figure 1

Magnetic splitting of the spin resolved density of states

as assumed in the Stoner model of itinerant magnetism.

Itinerant Electron Systems: Magnetism (Ferromagnetism)

342

The number of spin-up and spin-down electrons

is given by the integral over all occupied states,

where for T ¼0 K the upper limit can be taken as the

Fermi energy e

. In its original formulation, Stoner

assumed that the spin-up and spin-down bandstruc-

ture were equal so that the density of states N(e) are

the same for both spin directions. This treatment is

referred to as the rigid band picture, which assumes

that during the transition from a nonmagnetic to a

ferromagnetic state the spin-up and spin-down bands

do not change their shape and that they only become

shifted energetically by the spin splitting DE (c.f.

Table 1) given by:

DE ¼ IM ¼ Iðn

 n



Þð6Þ

In Eqns. (5) and (6), the quantity I is the Stoner

exchange factor and M is the magnetic moment.

From the Stoner equations the susceptibility can be

calculated which becomes:

w ¼

NðeÞ



1  I

NðeÞ



ð7Þ

where df/de is the energy derivative of the Fermi–

Dirac distribution. Equation (7) is the most general

form of the Stoner susceptibility which for T ¼0K

reduces to:

w ¼

Nðe

1  INðe

¼ 2m

Nðe

ÞS ð8Þ

which is the Pauli susceptibility 2m

N(e

) enhanced

by the exchange interaction via a factor S (Stoner

enhancement factor). If the term IN(e

) becomes

larger than 1, w becomes negative, which means that

the interacting electron gas is unstable against the

formation of a magnetic moment (spontaneous mag-

netic order). This gives rise to the formulation of the

famous Stoner criterion for the onset of magnetism

which happens if:

INðe

ÞX1 ð9Þ

Since the Stoner exchange factor I is an atom spe-

cific constant, a possible transition to a magnetic

state depends only on the density of states at the

Fermi energy N(e

). This in turn means that bands

are needed which are narrow enough to create a large

density of states. This is not only the explanation why

band magnetism occurs only in the 3d transition

metals (Cr, Mn, Fe, Co, and Ni) and the 5f-actinides

starting with curium. The band width of the 4d and

5d series is already too large, which implies that a

certain degree of localization is necessary.

If a system fulﬁlls the Stoner criterion and thus has

a magnetic ground state, Eqn. (7) also allows to

calculate the Curie temperature by requiring that T

is given by the temperature for which the denomina-

tor of Eqn. (7) becomes zero:

NðeÞ



de ¼ 1 ð10Þ

Eqn. (10) is a temperature dependent Stoner crite-

rion. Due to the convolution with the function df/de,

the effective density of states becomes progressively

smaller when the temperature rises until the relation

given above is fulﬁlled. Once this happens, the Stoner

theory does no longer see any magnetic moment so

that the paramagnetic state (the state above T

) is the

nonmagnetic state. This is a new mechanism com-

pared to the Weiss model, where the paramagnetic

state was given by complete disorder of the local

moments, or to the Heisenberg model within the

mean ﬁeld approximation, where the thermal agita-

tion leads to a breakdown of the interaction aligning

neighboring spins. Unfortunately the Curie temper-

atures calculated within the Stoner model are too

high by a factor of 4–8 (Gunnarsson 1976). The

thermal excitation mechanism is called single-particle

excitations or simply Stoner excitations. At T ¼0K

all states below the Fermi energy are occupied and all

states above are empty. With rising temperature the

softening of the Fermi–Dirac distribution creates

holes below the (T ¼0 K) Fermi energy and creates

occupied states above.

This is the typical case of an electron-hole excita-

tion or exciton, however, only excitations which are

connected with a spin ﬂip are able to reduce the bulk

magnetic moment. The energy scale on which these

single particle excitations occur is set by the T ¼0K

Fermi energy via the effective Fermi degeneracy tem-

perature T

2

Nðe



Nðe





ð11Þ

which depends on the local structure of the density of

states at the Fermi energy via its ﬁrst and second

energy derivative (Sommerfeld expansion). For most

systems this temperature is 5000 K to 10000 K so that

within the Stoner model hardly ever reaches a

reasonable order of magnitude. With the definition of

(which is basically the expansion of the integrand

of Eqn. (10)), T

can be written as:

¼ T

ðINðe

Þ1Þð12Þ

It is easy to see that T

only becomes considerably

smaller than T

if IN(e

) is only slightly larger than

one, which is the condition for the very weak itiner-

ant electron magnetism (Edwards and Wohlfarth

1968).

Systems under this class are supposed to have a

very low saturation magnetization and also a very

low T

. The progress in metallurgy and solid state

Itinerant Electron Systems: Magnetism (Ferromagnetism)

343

chemistry during the 1960s, mostly due to the search

for BCS-superconductors, led to the discovery of

a few candidates like ZrZn

,Sc

In, and Ni

Al.

Although their behavior below T

can be described

within the theory of weak itinerant ferromagnets, for

T4T

all three systems show a Curie–Weiss behavior

which is not consistent with the Stoner model.

Within the Stoner model the ﬁnite temperature

behavior of the susceptibility and the magnetic mo-

ment are described by the equation for the magnetic

isotherms of weakly itinerant systems:

MðH; TÞ

Mð0; 0Þ





MðH; TÞ

Mð0; 0Þ

1 



Mð0; 0Þ

ð13Þ

which represents the linear Arrott plots found also

experimentally. Explicitly the temperature depend-

ence of the magnetic moment is given by:

¼ 1 



1=2

ð14Þ

which for T-T

shows the expected mean ﬁeld be-

havior with a critical exponent b ¼

Eqn. (13) is equivalent to the Landau expansion of

the free energy of a ferromagnet which reads:

FðMÞ¼

 MH ð15Þ

The respective values of the coefﬁcients A and B

can easily be determined and become:

A ¼

1 



and B ¼

ð16Þ

where w

and M

are the susceptibility and magnetic

moment at the equilibrium, respectively.

The temperature dependence of the susceptibility is

a subject on its own. The functional dependence

above T

can easily be calculated from Eqn. (13) if

one considers, that for T4T

the magnetic moment

M(0, T) vanishes. The respective result is:

w ¼ 2w

 1



1

for T4T

ð17Þ

which allows to calculate the Curie constant C

deﬁned as:

C ¼

dðw

1

ð18Þ

which for the Stoner model varies linear in T rather

than being a ‘‘constant.’’

For temperatures below T

one has to consider the

additional temperature dependence of the magnetic

moment, so that the susceptibility becomes:

w ¼ w

1 



1

for TpT

ð19Þ

The reason for the surprising result that the sus-

ceptibility changes by a factor of two is not an ar-

tifact of the Stoner model, but is a general feature.

The reason for it lies in the fact that the susceptibility

simply measures the amount of magnetic moment

produced by an applied ﬁeld. The result means that it

is twice as easy to create the same moment from a

nonmagnetic spin system than from a magnetic spin

system, where the applied ﬁeld has to work against an

already magnetized ensemble. In both temperature

ranges, however, the inverse susceptibility does not

show a Curie–Weiss law, but always a T

behavior.

Although the Stoner model gives a very good de-

scription of the T ¼0 K ground state properties, its

ﬁnite temperature behavior fails completely. The

electron-hole excitations considered are not able to

yield reasonable values for T

and also lead to the

wrong power law for the w versus T dependence.

1.2 The Hubbard Model

Parallel to the development of bandstructure theory

there was a search for ‘‘simple’’ toy models to explain

solid state magnetism. The Hubbard model combines

electron hopping between neighboring sites and the

Coulomb repulsion of electrons at the same site.

These features are combined within the Hubbard

Hamiltonian (Hubbard 1963), which in its simplest

form reads:

H ¼

ijs

þ U

ð20Þ

The electron hopping is controlled by the para-

meter t

, U models the Coulomb interaction. c

; c

are the fermion creation and annihilation operators

for an electron with spin s on site i and n

¼ c

the related ladder operator counting the occupation

on site i. These fermion operators obey the following

anticommutator rules:

½c

; c

¼@

½c

; c

¼½c

; c

¼0 ð21Þ

Depending on the sign of U the Hubbard Hamil-

tonian describes various phases, i.e., (i) U40 (repul-

sive) paramagnetic metallic, ferromagnetic metallic,

and antiferromagnetic insulating; and (ii) Uo0

(attractive) normal Fermi liquid, superconducting,

charge density wave (insulator), and normal Bose

liquid (insulator).

U is, however, not the only parameter. There exists

also the strength of the electron hopping t

and the

temperature T. Further ‘‘hidden’’ variables are the

dimensionality of the system and the structure of

Itinerant Electron Systems: Magnetism (Ferromagnetism)

344

the crystal lattice. Since the band ﬁlling (thus the

number of electrons) plays an important role also

the electron density n ¼n

þn

can be regarded as a

parameter of the Hubbard Hamiltonian. Since the

Pauli principle avoids that two electrons with like

spin occupy the same lattice site then n

p1 for

s ¼m, k and thus np2. The special case n ¼1

describes the half-ﬁlled band (antiferromagnetism).

A straightforward solution can be found in the

unperturbed case U ¼0. The solution is found by

the Fourier transform of the respective operator. In

the time dependent form

ı_

’

¼

) c

ﬃﬃﬃﬃ

ikR

ð22Þ

ı_

’

ðtÞ¼e

ðtÞ)c

ðtÞ¼e



ð0Þð23Þ

which as a solution describes a single electronic band

in the tight binding limit:

¼ e



jai

ikðR

R

ð24Þ

For a 2d square lattice e

¼2t(cos(k

a) þ

cos(k

a)) leading to a bandwidth W ¼4t.

In a similar way one treats the case for Ua0in

the Hartree–Fock approximation where the Hubbard

interaction n

is replaced by

þ n



. The entities

are thermodynamical ave-

rages which have to be determined self-consistently.

The physical interpretation of the Hartree–Fock

approximation is that ﬂuctuations in the double

occupancy n

are suppressed. The respective time-

dependent Schro

dinger equations reads:

 e

 U

is



¼

ð25Þ

The solutions are two bands split by the Hubbard

interaction U:

¼ e

Uð

n þ mÞ; e

¼ e

Uð

n  mÞð26Þ

with

n þ mÞ;

n  mÞð27Þ

The respective band splitting is thus given by

DE ¼Um ¼e

 e

, which can directly be compared

to the result obtained from the Stoner model (Eqn.

(6)). In complete analogy to the Stoner model one

also arrives at a criterion for magnetic ground state

which is fulﬁlled if UN(e

)X1 (c.f. Eqn. (9)).

It is found that within the Hartree–Fock appro-

ximation the Hubbard model and the Stoner model

become equivalent. The suppression of ﬂuctuations

in the double occupancy leads to an effective mean

ﬁeld treatment where Um represents the resulting

self-consistent molecular ﬁeld.

The missing physics is again the orientational dis-

order. This is well described by the Heisenberg model

but hard to see for itinerant electrons where in the

Hartree–Fock approximation the paramagnetic state

becomes the nonmagnetic state. However, what is

required for the paramagnetic state is that the ave-

rage over the magnetic moments vanishes:

ðn

 n

ð28Þ

but the individual moment at site i remains, so that

¼n

n

a0 for times t such that

ptp

1.3 Spin Fluctuations

From the preceding discussion it becomes clear that

also in itinerant systems collective excitations of the

spin system govern the ﬁnite-temperature properties.

In the mid-1970s the ﬁrst self-consistent spin polarized

bandstructure calculations of the ground state of

transition metals were performed using the LSDA to

treat exchange and correlation effects. These calcula-

tions yielded satisfactory values for the magnetic mo-

ment, the exchange splitting, the cohesive energy, and

a magnetic ground state which could be explained

within the Stoner model. However, any attempt to

explain the ﬁnite temperature behavior from these re-

sults failed. In the light of the previous discussion this

failure is nowadays no longer surprising. Although

these calculations contain all the many-body interac-

tions via the density functional formalism, they still

lack the ability to describe an excitation spectrum be-

yond the single particle picture. It has become clear

(see review Shimizu 1981), that the problem is caused

by imposing the translational symmetry of the spin

density, an assumption which becomes violated by the

collective excitations for T40 K. This breakdown of

the conventional band picture has led to three main

directions to go beyond it.

(i) In the Murata and Doniach (1972) approach

the properties of the magnetic systems are described

via a Landau–Ginzburg expansion of the free energy.

The effect of spin ﬂuctuations is formulated via ran-

domly ﬂuctuating local magnetic moments which

couple to the bulk magnetization. Although these

local moments m(r) are vectors, the averaging process

using Gaussian statistics leads to scalar quantities

/mðrÞ

S, which simply renormalize the original

Landau expansion for a ferromagnet (Eqn. (15)). This

scheme was successfully applied by Lonzarich and

Taillefer (1985) to ferromagnetic and nearly ferro-

magnetic metals.

(ii) In the disordered local moment approach, the

magnetic moments on individual atoms are allowed

Itinerant Electron Systems: Magnetism (Ferromagnetism)

345

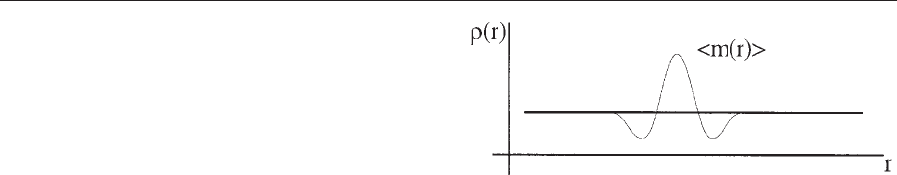
to have random orientations in the sense described by

Herring (1952a, 1952b) and later by Hubbard (1979a,

1979b) and Hasegawa (1980). Pindor et al. (1983)

implemented this model in a self-consistent Kor-

ringa–Kohn–Rostoker (KKR) Coherent-Potential-

Approximation (CPA) calculation to simulate the

magnetic properties of the transition metals at ﬁnite

temperature. Within this formalism Staunton et al.

(1984) calculated the temperature dependent spin

density and the wave vector-dependent susceptibility

w(q). With this model T

values of 1260 K and 225 K

for iron and nickel were obtained, which should be

compared to experimental values of 1043 K and

630 K, respectively. The discrepancy between theo-

retical and experimental values could be due to the

assumption that directional disorder is complete

above T

, so that effects of short range order are

neglected which could be important as suggested

by Prange and Korenman (1979a, 1979b) and

Capellmann (1979). However, what these CPA calcu-

lations have clearly shown is that the density of states

(and thus all related macroscopic quantities) remain

virtually unchanged up to temperatures well above

the Curie point.

(iii) Later Nolting et al. (1995) proposed a new

approach where the LSDA ground state bandstruc-

ture is ﬁtted to a tight-binding model which enters a

Hubbard Hamiltonian. The idea of this treatment is

to start from the best quantum mechanical ground

state available and to use it as a basis for a many

particle treatment within the Hubbard model, which

also allows correction for the too small correlation in

the usual LSDA schemes. The calculated T

values

for Fe, Co, and Ni are in excellent agreement with

experimental values. What makes this approach even

more promising is the fact that it explains the exper-

imental photo-electron spectra which could not be

related to the bare LSDA bandstructure results.

1.4 Fluctuations of the Magnetic Moment

The idea of the introduction of ﬂuctuations is to ac-

count for the shortcoming of the Stoner model, which

does not allow for any tilting of the spins. In addi-

tion, these ﬂuctuating moments which are induced by

temperature should give rise to a Curie–Weiss be-

havior of the susceptibility. Such a ﬂuctuation is

shown in Fig. 2.

For the gas of free electrons the eigenfunctions are

plane waves and the charge and spin density are con-

stant in space. A local ﬂuctuation (here it is only a

parallel component) can be seen as a perturbation of

the ground state spin density with a ﬁnite lifetime well

below the characteristic time for electron hopping. It

can also be assumed that the spatial extension of the

ﬂuctuation is larger than the range of interaction in

the system, which means that ﬂuctuations are treated

in the limit of long wavelength.

In the framework of the Landau theory of phase

transitions the bulk magnetic moment M was intro-

duced as the order parameter for the free energy

(Eqn. (15)). With this choice it was assumed that any

vector properties of M were irrelevant for the results,

since time reversal symmetry requires that only even

powers of M enter the free energy. Introducing local

ﬂuctuations of the magnetic moment one has to

recognize the vector properties of both the mag-

netic moment M and its ﬂuctuation m(r). Conse-

quently one has to distinguish ﬂuctuations which are

parallel and which are perpendicular to the direction

of M. In the ﬂuctuation treatment one replaces the

order parameter M in Eqn. (15) by a new quantity

which, in addition, contains the ﬂuctuating magnetic

moment:

-/ðM þ

S ð 29Þ

The bracket /?S denotes the Gaussian average

and the index of m represents the three components

of the ﬂuctuation in the local coordinate system of M.

Unambiguously it can be assumed that M points into

the z direction, which (for an isotropic system) leads

to two components of the ﬂuctuation which are per-

pendicular to M, namely m

and m

, and one parallel

component, m

. To simplify the legibility the obvious

r dependence of m(r) is omitted. As an example the

square of the order parameter is given in:

/ðM þ

S ¼ /M

þ2M

þ 2/m

S þ /m

S ð30Þ

When averaged the mixed term vanishes because m

always appears with an odd power. From the term

, for the same reason, only the diagonal elements

remain. In the resulting relation the subscripts were

replaced by symbols denoting the perpendicular com-

ponents m

and m

and the parallel component

One now replaces the order parameter M

in the

free energy expression (Eqn. (15)) by the respective

new order parameter /ðM þ

S and obtains

Figure 2

Schematic depiction of a local, longitudinal ﬂuctuation

of the spin density r(r) (thick horizonal line) of the

electron gas.

Itinerant Electron Systems: Magnetism (Ferromagnetism)

346

the ‘‘dynamical’’ form for the free energy F:

F ¼

ðM

þ 2/m

S þ /m

SÞ

ðM

þ M

ð6/m

S þ 4/m

SÞ

þ 8/m

þ 3/m

þ 4/m

S/m

SÞð31Þ

The original static form of F has just been extended

by the ﬂuctuations. For T ¼0 K, the ﬂuctuations

vanish and Eqn. (31) reduces to Eqn. (15). Since the

ﬂuctuations only renormalize the original Landau

coefﬁcients, the physical meaning and definition of

both A and B are the same as before. What can be

seen immediately is that even when the bulk magnet-

ization M vanishes, the ﬂuctuations are present at all

temperatures since they represent thermally induced

local magnetic moments so that the paramagnetic

state (for T4T

) is no longer the nonmagnetic state

as in the Stoner model.

This expression for the free energy can now be used

to derive important properties of the ﬂuctuating mo-

ments. Since T

is given by the temperature where the

susceptibility diverges under the condition that the

bulk magnetic moment M vanishes, one can calculate

the amplitude of the ﬂuctuations at T ¼T

¼ w

1

¼ A þ

ð10/m

SÞ¼0 for T ¼ T

ð32Þ

In Eqn. (32) the subscripts for the parallel and

perpendicular component disappear, since when M

vanishes a distinction between directions parallel and

perpendicular to M no longer has any meaning.

Using Eqn. (16) the ‘‘Moriya formula’’ is recovered:

S ¼

at T ¼ T

ð33Þ

which demonstrates that the mean square amplitude

of the ﬂuctuation at T

is a ground state property.

Based on these results and inspired by the work of

Lonzarich and Taillefer (1985), Mohn and Wohlfarth

(1986) derived a simple model for the Curie temper-

ature in weakly itinerant systems which reads:

10w

ð34Þ

Here T

is the Curie temperature caused by the

spin ﬂuctuations. Eqn. (34) describes the long wave-

length limit (q-0) for weakly itinerant magnets and

is thus an approximation which is based on the as-

sumption of an effective cut-off for the collective ex-

citations which should be fairly constant. In the

present literature this approach in known as the

Mohn–Wohlfarth model and has triggered consider-

able interest in the application of spin ﬂuctuation

theory. Although the approach can be expected to

break down for strong ferromagnets (Qi et al. 1994) it

can still be used to describe the relative change of T

(Jaswal 1993), e.g., for different concentrations in an

alloy system.

From the dynamical form of the free energy

(Eqn. (31)) it is straightforward to calculate the spe-

cific heat and its discontinuity at T

(Mohn and

Hilscher 1989a). The specific heat becomes linear in

temperature and that the discontinuity at T

is re-

duced by a factor of four with respect to the Stoner

result, which is due to the fact that the paramagnetic

state (above T

) is no longer the nonmagnetic state:

ð35Þ

As for the specific heat, spin ﬂuctuations also have

a major impact on the magnetomechanical properties

and it has been shown that their presence not only

reduces the spontaneous magnetostriction with re-

spect to the Stoner model in the desired way, but also

leads to a different (linear) pressure dependence of T

(Mohn et al. 1987):

ðPÞ

ðP ¼ 0Þ

¼ 1 



ð36Þ

where P

is the critical pressure for the disappearance

of magnetism.

In addition, the temperature dependence of the

bulk magnetization differs from the Stoner result

(Eqn. (14)) and reads:

¼ 1 



1=2

ð37Þ

For low temperatures the reduction of the mag-

netic moment is stronger than in the Stoner model.

The reason is the same as for the comparison of the

Weiss and Heisenberg models, i.e., the collective

modes described by the spin ﬂuctuations can readily

be excited at low temperature, where the Stoner ex-

citations are still very small.

About at the same time Entel and Schro

ter (1988,

1989), Mohn et al. (1989b), and Wagner (1989)

showed how bandstructure results derived from the

‘‘ﬁxed spin moment’’ (FSM) method (Schwarz and

Mohn 1984) can be implemented into the spin ﬂuc-

tuation theory. An explicit expression for the ﬂuctu-

ating magnetic moment can be derived from a

Landau–Ginzburg expansion for the free energy,

which also contains a gradient term to describe the

local variation of the ﬂuctuations:

H ¼

dr½EðM þ mðrÞÞ þ

ðr

ð38Þ

E(M þm( r)) is the dynamical form of the free en-

ergy as given by Eqn. (31). In addition, a quadratic

gradient term is added containing a new coefﬁcient K,

Itinerant Electron Systems: Magnetism (Ferromagnetism)

347

which measures the strength of the spin ﬂuctua-

tions. It should be noted that K is analogous to the

spin wave stiffness constant which appears in the

Heisenberg model.

To calculate the free energy the partition function

must be evaluated by integrating over all ﬂuctuation

variables. Since this integration cannot be carried out

analytically for the assumed Hamiltonian one ap-

proximates the result by using the Peierls–Feynman

(Peierls 1936, Feynman 1955) inequality which rep-

resents an effective mean-ﬁeld treatment:

FpF

þ /H  H

ð39Þ

For the trial Hamiltonian the lowest order trans-

lationally invariant quadratic form in the ﬂuctuations

m(r) is chosen:

i¼1

ðr  r

Þm

ðrÞm

ðr

Þð40Þ

where O

(rr

) is used as a variational parameter to

determine the optimal solution. It should be noted

that the form used in Eqn. (40) resembles the Hei-

senberg–Hamiltonian, where the localized spins on

the lattice sites i and j are replaced by ﬂuctuating

moments located on positions r and r

. For the tem-

perature dependence of the ﬂuctuating moment:

S ¼

4pk

@/m

dk ð41Þ

The function j is that part of the energy functional

which depends on the ﬂuctuations:

f ¼

r/EðM þ mðrÞÞ  EðMÞS ð42Þ

In Eqn. (41) there appear two unknown parame-

ters: the ‘‘spin wave stiffness’’ K and the cut-off wave

vector k

. The latter quantity must be introduced,

since the Ornstein–Zernicke correlation function,

which appears in the integrand, leads to a divergence

if the integration is carried out to k-N. A physical

justiﬁcation for the introduction of this cut-off may

be found in the strong damping of the spin ﬂuctu-

ations by the single particle excitations for k vectors

larger than a critical value. From the zero-tempera-

ture properties of the derivative of in j the integrand

of Eqn. (41) the spin wave stiffness constant K by x

where x is the correlation length and w

is the sus-

ceptibility can be replaced. Since @j/@/m

S must

vanish at T ¼T

, integration at T

obtains a result

similar to the Mohn–Wohlfarth model:

10w

ð43Þ

In addition to Eqn. (34), here also the ﬁnite wave-

length dependencies of the ﬂuctuations are included

which should lead to a wider applicability.

2. Examples

Historically it is assumed that the 3d transition metals

are the prototypical representatives of itinerant elec-

tron magnets. They have noninteger magnetic mo-

ments and thus cannot be explained on the basis of

any local moment model. However, the ideal ‘‘Stoner

system’’ would rather be free electron like. This is

somehow realized in the simple metals, which, due to

the large bandwidth of the s electrons, are unfortu-

nately all nonmagnetic. The key magnetic proper-

ties of the magnetic 3d transition metals are given in

Table 2.

Phenomenologically one distinguishes between two

classes of itinerant electron magnetic systems named

weak- and strong ferromagnets. Their major proper-

ties are described as follows:

(i) Weak itinerant ferromagnets: majority carrier

(spin up electrons) bands are not completely ﬁlled;

minority bands often empty, unsaturated magnetic

moments, large susceptibility, strong pressure de-

pendence of the magnetic moment and the Curie

temperature (alloys of iron with metals and metal-

loids with less than half-ﬁlled valence bands such as

Fe–V, Fe–Cr, Y–Fe, Zr–Fe, etc. b.c.c. Fe).

(ii) Strong itinerant ferromagnets: majority carrier

bands completely ﬁlled; minority bands partially

ﬁlled, saturated magnetic moments, small suscepti-

bility, small (often vanishing) pressure dependence

of the magnetic moment and the Curie temperature

(alloys of iron, cobalt, and nickel with metals and

metalloids with more than half-ﬁlled valence band

such as Fe–Co, Fe–Ni, Ni–Co, Ni–Cu, Ni–Zn, etc.,

h.c.p. Co, f.c.c. Ni, and f.c.c. Fe).

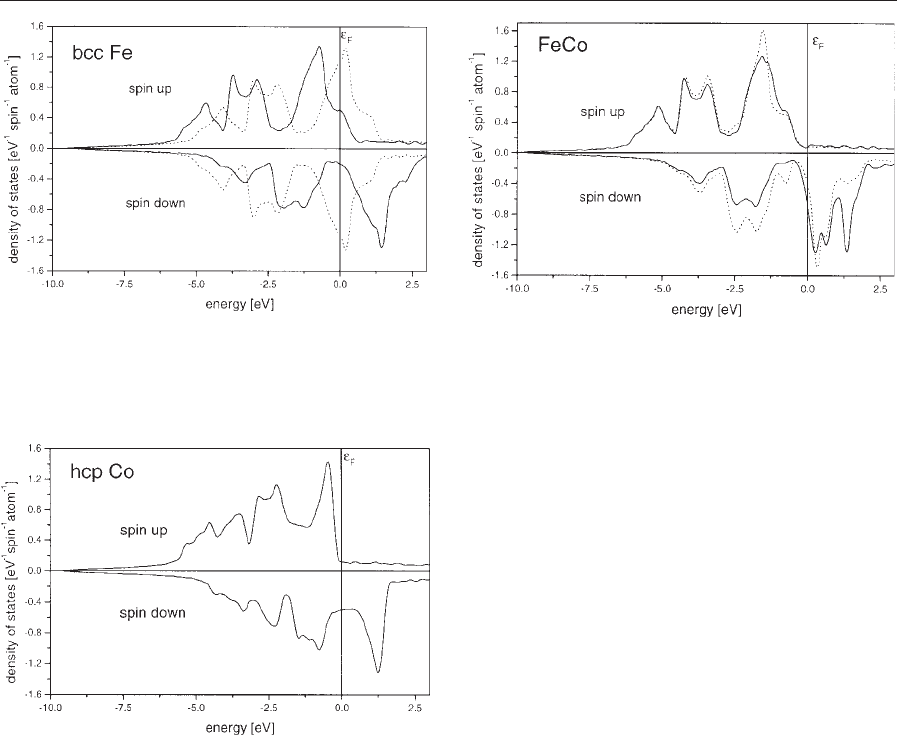
An example for the ﬁrst group of weak itinerant

electron magnets is given in Fig. 3, where the spin

resolved density of states (DOS) of b.c.c. iron is

shown. For the spin-polarized case (full line) the

Fermi energy e

intersects the majority band just

before the upper edge of the d band. For the minority

band e

is located in a minimum of the DOS, a

Table 2

Magnetic moment M in emu/g and in multiples of m

and the T

values for the ferromagnetic 3d transition

metals Fe, Co, and Ni.

M (emu g

1

) M (m

) T

(K)

Fe 222 2.22 1039

Co 163 1.65 1390

Ni 58 0.62 630

Itinerant Electron Systems: Magnetism (Ferromagnetism)

348

position which is highly favorable in energy. Thus

b.c.c. iron is an example for a system with an un-

saturated magnetic moment. The dotted line shows

the DOS for the hypothetical nonmagnetic state

(majority and minority DOS are equal). The Fermi

energy e

lies in a region of rather large DOS, which

is a prerequisite to fulﬁll the condition given by the

Stoner criterion (Eqn. (12)). An example for the

strong itinerant case is found in Fig. 4 for h.c.p. co-

balt. The additional valence electron saturates the

majority band, so that e

lies above the spin up d

band. This is the typical result for this class of itin-

erant ferromagnets, the resulting low DOS at e

causes the small susceptibility observed. For both

b.c.c. iron and h.c.p. cobalt, it can be observed that

the shape of the majority and minority DOS is almost

equal. For these monoatomic solids spin polarization

only produces a mutual shift between the spin up and

spin down bands (see Fig. 1) an effect which is known

as the rigid band picture. The resulting spin splitting

can, for example, be measured from the energy dif-

ference of the respective DOS peaks in the middle of

the d bands. The respective value for DE is 1.49 eV,

which according to Eqn. (6) yields a Stoner exchange

factor, I, of 0.98 eV.

In the case of magnetic alloys the rigid band pic-

ture breaks down. As an example the DOS for FeCo

(in the CsCl structure) is shown in Fig. 5.

From the completely ﬁlled majority band it is ob-

vious that FeCo is a strong ferromagnet. Due to the

interaction with the neighboring cobalt atoms, the

magnetic moment of iron is increased to 2.6 m

mak-

ing iron a strong ferromagnet (in contrast to b.c.c.

iron). The moment per cobalt atom is 1.7 m

which is

only a minor increase compared to h.c.p. cobalt

which already shows strong ferromagnetism. The

density of states also nicely shows the inﬂuence of

the spin splitting on the binding mechanism. For the

majority spin both the iron and the cobalt d band are

very much alike. For both constituents the spin up d

band is ﬁlled and between the two atomic species a

so-called common band is formed. In the minority

band strong differences in the height of the iron and

cobalt DOS are visible. Below e

the cobalt DOS is

larger than the iron DOS and vice versa above e

This behavior is needed to accommodate the addi-

tional electron of cobalt. In general this kind of spin

dependent interaction has been described as covalent

magnetism (Williams et al. 1982).

As a general feature it must be mentioned that pure

itinerant electron magnetism hardly ever occurs. The

most prominent candidates for this extreme model

are ZrZn

and Ni

Al, both having very small mag-

netic moments and very large susceptibilities leading

to small T

values. In most other magnetic transition

Figure 3

Spin resolved density of states for the spin polarized

(solid line) and the nonmagnetic case (dotted line) for

b.c.c. Fe.

Figure 4

Spin resolved density of states for the strongly itinerant

ferromagnet h.c.p. Co.

Figure 5

Spin and atom resolved density of states for FeCo (CsCl

structure). Fe DOS (solid line), Co DOS (dotted line).

Itinerant Electron Systems: Magnetism (Ferromagnetism)

349