Burton T. (et. al.) Wind energy Handbook
Подождите немного. Документ загружается.


rules. Thus, for a ply reinforced by UD fibres, the longitudinal stiffness modulus,
E
1
, can be derived accurately from the rule of mixtures formula
E
1
¼ E
f
V
f
þ E
m
(1 V
f
)(7:3)
where E
f
is the fibre modulus (72.3 GPa for E-Glass), E
m
is the matrix modulus (in
the range 2.7–3.4 GPa) and V
f
is the fibre volume fraction. On the other hand, the
inverse form of this formula, e.g.,
1
E
2
¼
(1 V
f
)
E
m
þ
V
f
E
f
(7:4)
significantly underestimates the transverse modulus, E
2
, and the in-plane shear
modulus, G
12
. More accurate formulae based on more soph isticated models are
given in Barbero (1998).
The longitudinal tensile strength of a ply reinfor ced by UD fibres,
1t
, can be
estimated from:
1t
¼
fu
V
f
þ
E
m
E
f
(1 V
f
)
(7:5)
where
fu
is the ultimate tensile strength of the fibres. However, the tensile
strengths of E-glass single fibres (3.45 GPa) cannot be realized in a composite, where
fibre strength reductions of up to 50 percent have been measured. Accordingly, a
value of
fu
of 1750 MPa should be used in Equation (7.5).
The longitudinal compressive strength of a ply reinforced by UD fibres is always
significantly less than the tensile strength because of microbuckling of the fibres,
which is governed by the shear strength of the matrix and the degree of fibre
misalignment. A strength reduction of at least 15 percent should be allowed for,
assuming minimum fibre misalignment.
Clearly, longitudinal stiffness and strength are both limited by the fibre volume
fraction obtainab le. For hand lay-up, fibre volume contents of 30–40 percent are
typical, but the use of ‘vacuum bagging’, in which trapped air and excess volatile
compounds, such as residual solvent, are extracted, consolidates the composite and
allows a volume fraction of 50 percent or more to be achieved. The use of ‘pre-
pregs’, which are unidirectional fibres or woven fabric pre-impregnated with
partially cured epoxy resin, resu lts in similar increased fibre volume fractions.
Fatigue properties
When expressed in terms of stress, the fatigue properties of composite laminates
extend over a wide range, depending on fibre volume fraction and the number of
plies with fibres in the longitudinal direction. However, data from constant stress
amplitude fatigue test results become much more intelligible if stress ranges are
converted into initial strain ranges, allowing the fatigue properties of composites
with different lay-ups to be compared. (The Young’s modulus of a composite
BLADES 385
reduces over time during a fatigue test – hence the need to specify that the strain
range is measured at the start of the test.)
The fatigue behaviour of composites depends on both the stress range and the
mean stress level, which can both be described in terms of the maximum stress,
max
, and the ratio of minimum to maximum stress, R. It is convenient initially to
consider fatigue behaviour under reverse loading, i.e., with R ¼1, for which the
mean stress is zero, and then relate behaviour at other R ratios to it.
The constant amplitude fatigue behaviour of glass-fibre composites can best be
characterized by a linear relationship between the logarithm of the number of cycles
and the logarithm of the stress or strain amplitude, viz:
¼
0
N
1=m
or N ¼ K
m
where K ¼ (
0
)
m
or log N ¼ log K m log (7:6)
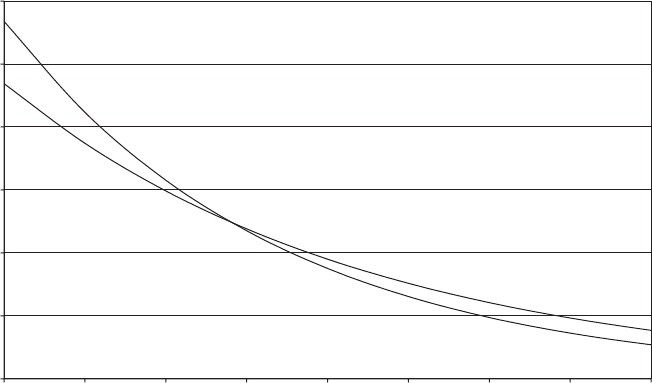
Echtermeyer, Hayman and Ronold (1996) carried out a reg ression analysis on a total
of 111 constant amplitude, reverse loading fatigue test results for 10 different
laminates tested at DnV, assuming that they all conformed to the same –N curve,
and obtained values for
0
, log K and m of 2.84 percent, 3.552 and 7.838 respectively,
with a standard deviation of log N of 0.437. The DnV regression line is compared
with another derived from 19 tests on a 08/þ458, 458 laminate at ECN, giving
0
¼ 2:34 percent, log K ¼ 3:775 and m ¼ 10:204, in Figure 7.5. The researchers did
not constrain the regression lines to pass through the strain value at either UTS or
UCS at log N ¼ 0(ca 2.4 percent and 2.0 percent); had they done so the DnV line
would have had a shallower slope, i.e., a larger value of m. After comparison with
regressions on other fatigue test datasets, they concluded that the DnV line
provided a reasonable basis for initial design.
0
0.5
1
1.5
2
2.5
3
012345678
Log (No. of loading cycles)
Initial strain amplitude (%)
DnV: log N = 3.552 - 7.838 log(strain)
ECN: log N = 3.775 - 10.204 log (strain)
Figure 7.5 Strain-life Regression Lines Fitted to Results of Constant Amplitude, Reverse
Loading Fatigue Tests on GFRP Composites
386
COMPONENT DESIGN
In the GL rules, the –N curve fo r design takes the same form as Equation (7.6)
for the case of reverse loading, but
0
is set equal to the strain at ultimate te nsile
load and partial materials safety factors are included. GL specifies different values
of the index, m, for composites with polyester and epoxy matrixes – 9 and 10
respectively – although opinion is divided as to whether the difference is justified.
Constant amplitude tests at other R ratios generally show reducing fatigue lives
as the mean stress increases above zero – whether in tension or in compression. It is
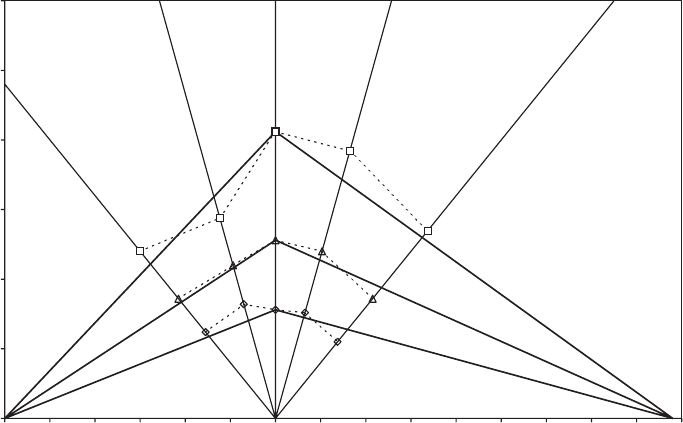
customary to represent the results on a constant life diagram (also known as a
Goodman diagram), in which the stress range to failure is plotted against mean
stress for different fatigue lives. Regression analyses can be carried out on families
of test results at different R ratios to give a ser ies of –N relations in the form of
Equation (7.6) which can be used to plot the constant life diagram. Such an exercise
was carried out on the Dutch ‘FACT’ database of fatigue tests on composites for
wind turbines (Joose and van Delft, 1996), and some results of this work have been
reproduced in Figure 7.6 (dashed lines).
In the preparation of design rules, it is common practice to make the simplifying
assumption that the strain amplitude reduces linear ly with increasing mean strain
for a given fatigue life, reaching zero at a mean strain corresponding to either the
ultimate tensile or compressive strength. Such linear constant life lines are shown in
Figure 7.6 as heavy lines. Constant life lines for design are obtained from character-
istic material properties divided by appropriate partial safety factors, as opposed to
the characterisitc properties used in Figure 7.6. Thus the design strain amplitude
when the mean stress is compressive becomes:
0
0.25
0.5
0.75
1
1.25
1.5
-1.5 -1.25 -1 -0.75 -0.5 -0.25 0 0.25 0.5 0.75 1 1.25 1.5 1.75 2 2.25
Mean strain (%)
Strain amplitude (%)
R = 9
R = -2.5
R = -1
R = -0.4
R = 0.111
N = 10
3
N = 10
5
N=10
7
Figure 7.6 Constant Life Diagram Showing Variation in Fatigue Strain Amplitude with
Mean Strain for Lives of 10
3
,10
5
and 10
7
Cycles for GFRP Composites
BLADES 387

d
( , N) ¼
0d
N
1=m
1
cd
(7:7)
where
0d
¼
0k
=ª
mf
,
cd
¼
ck
=ª
mu
,
0
is the value of given by the –N curve when
log N is zero,
is the mean stress for the loading cycles under consideration, and
cd
is the design compressive stress. ª
mf
is the partial safety factor for fatigue
strength, ª
mu
is the partial safety factor for ultimate strength, and the suffices d and
k signify design and characteristic values respectively.
Equation (7.7), together with its equivalent for mean tensile loading, can be used to
calculate the permissible number of load cycles, N
i
, for each strain range in the fatigue
loading spectrum for the point in the blade cross section under examination –
incorporating the appropriate partial safety factor for the consequences of failure .
Thesearethencombinedwiththe predictednumberofcyclesforeachstrainrange, n
i
,to
yield Miner’s damage sum,
P
i
(n
i
=N
i
),which is normally required to be less than unity.
There is inevitably a degree of uncertainty as regards the accuracy of Miner’s rule
in predicting the fatigue damage due to variable amplitude loading from constant
amplitude test data. In order to investigate this, fatigue test programmes have been
carried out using the WISPER (Wind SPEctrum Reference) and WISPERX variable
amplitude fatigue load spectra, which have been devised to be representative of
those experienced by wind turbine blades. (WISPERX is a modification of WISPER
in which the large number of small cycles, accounting for approximately 90 percent
of the total, are omitted to reduce test durations.) For each test specimen, the
WISPER (or WISPERX) load sequence is scaled to give a chosen maximum stress
level and applied repeatedly until the specimen fail s.
Van Delft, de Winkel and Joose (1996) analysed the results of a series of tests carried
out at ECN and Delft Technical University on a 08, 45 8 laminate and found that, for a
maximum stress of about 150 MPa, the actual fatigue lives of specimens subjected to
repetitions of the WISPER or WISPERX load sequences were about 100 times less than
predicted for these sequences on the basis of constant amplitude, reverse loading test
data and Miner’s rul e, with the effect of mean stress allowed for using the linear
relation described above. The R ¼1 test data led to an S–N curve given by
N ¼ ( =
tu
)
10
, where is the amplitude of the stress cycles and
tu
is the ultimate
tensile strength, so the number of cycles to failure for constant amplitude loading at
other R values was taken as N ¼ ( =
tu
(1 =
tu
))
10
for a tensile mean and
N ¼ ( =
tu
(1 =
cu
))
10
for a compressive mean in calculating the Miner’s damage
sum. The difference in fatigue lives at the stated maximum stress level quoted above
translates to an approximate ratio of 1:1.5 between actual and predicted maximum
stress levels of the WISPER sequence to cause failure over the design fatigue life, which
would clearly use up a substantial proportion of the safety factors used in design.
However, other investigators working with different laminates have found reasonable
agreement between measured and predicted fatigue lives under WISPER loading.
Material safety factors
Limit-state design requires that the characteristic strength of a material be divided
by a partial safety factor for material strengt h. In the case of GFRP, this factor needs
388 COMPONENT DESIGN
to take account of degradation of the material over time , as well as the material’s
inherent variabi lity.
The GL rules lay down that the material safety factor for calculating the design
strength of GFRP under extreme loads is to be calculated as the product of
• a basic factor, ª
MO
, of 1.35
• a factor, C
2a
¼ 1:5, to account for the influence of ageing,
• a factor, C
3a
¼ 1:1 to account for strength reduction at higher temperatures,
• a factor, C
4a
¼ 1:2 for hand lay-up laminates or 1.1 where manufacture is partially
automated,
• a factor, C
5a
¼ 1:1 if the laminate is not post cured.
These rules result in a material safety factor in the range 2.45–2.94. In the case of
fatigue loads, the ageing factor of 1.5 is omitted and the factor acco unting for lay-up
is replaced by one taking account of the type of fibre reinforcement.
7.1.7 Properties of wood laminates
Although laminated wood/epoxy is classed as a composite, it is markedly different
in form from GFRP. Individual plies are made up of large sheets of wood veneer
(Figure 7.7) in stead of a multiplicity of fibres laid up in a matrix, and the epoxy
behaves as an adhesive rather than a matrix, bonding the sheets together at the
longitudinal and transverse joints and bonding each ply to its neighbour. Thus
the fibre volume fraction is close to 100 percent and the anisotropic properties of the
wood laminate derive principally from the anisotropic properties of the wood itself.
Wood strength properties are much greater in the direction parallel to the grain,
so all the veneers are orientated with the grain parallel to the blade axis, in order to
resist blade-bending loads efficiently. However, the veneers cannot be produced in
lengths much greater than 2.5 m, so transverse joints have to be included, which
introduce lines of weakness not normally found in GFRP blades. The effect is
minimized by staggering the joints, and by using scarf joints in preference to butt
joints.
The epoxy adhesive has a secondary function of sealing the veneers against
moisture ingress; additional moisture protection is provided by a layer of glass/
epoxy on both the external and internal surfaces. It is important to maintain
moisture content at a low level, because veneer strength decreases about 6 percent
for every 1 percent rise in moisture content.
A comparison of some of the properties of wood laminates used, or considered
for use, in wind turbine blades is given in Table 7.2. Khaya ivorensis, an African
mahoghany, and Douglas fir used to be the main species used for blade man ufac-
ture in the UK and US respectively, but environmental pressures have led to the
phasing out of Khaya in favour of European species such as poplar and birch.
The table gives tensile strengths of unjointed specimens. Bonfield et al. (1992)
report the results of tests on jointed specimens, which showed a significant
BLADES 389

reduction in tensile strength to 50 MPa for butt jointed Khaya. Scarf jointed Khaya
specimens, with a 1:6 length to thickness ratio, performed much better, achieving a
tensile strength of 75 MPa. In all cases the joints in the different veneers making up
the laminate were staggered.
An important consideration for design is the variability of strength properties,
particularly as wood is an inherently variable material. Strength tends to increase
with density, and density varies according to the growing conditions of the tree and
Figure 7.7 Blade Production. View of Veneer Lay-up in Mould to Make One Blade Skin.
The Blade is Completed by Glueing Face and Camber Skins Together. (Reproduced by
permission of NEG-Micon)
Table 7.2 Properties of Unjointed Wood/Epoxy Laminates
Species Specific
gravity
Mean tensile
strength
along the
grain
(MPa)
Mean
compression
strength
along the
grain (MPa)
Young’s
Modulus
along the
grain
(GPa)
Shear
strength
(MPa)
Khaya ivorensis 0.55 82 50 10 9.5
Poplar 0.45 63 52 10 9
Baltic pine 0.55 105 40 16
Birch 0.67 117 81 15 16
Beech 0.72 103 69 10 16
Douglas fir 0.58 100 61 15 12
390
COMPONENT DESIGN
the part of the tree from which the wood is taken. Such variability can be reduced
by careful grading and the rejection of damaged veneers before laminating. Bonfield
and Ansell (1991) report compression tests on 32 carefully selected Khaya samples
which yielded the compression strength of 50 MPa given in the table with a
standard deviation of only 3 MPa. It should be noted that the lack of annual growth
rings in equatorially grown wood may reduce the degree of scatter. Wood strengths
perpendicular to the grain are typically much less than those along the grain – for
example, the compressive strength of transversely loaded Khaya is only 12.6 MPa.
Fatigue properties
The fatigue properties of wood laminates have been the subject of a sustained
programme of work at Bath University, starting with Khaya and then extending to
other species (Bonfield et al. (1992)). A useful summary of this work appears in
Bond and Ansell (1998). The general conclusion is that wood performs very well in
fatigue with a shallow S– N curve slope, and that fatigue strengths at high cycles do
not vary greatly between species.
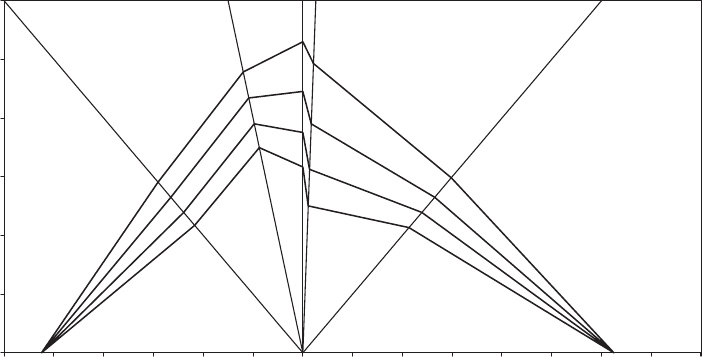
If the S– N curve for constant amplitude, reverse loading (R ¼1) fatigue is
normalized with respect to the ultimate compressive strength,
cu
– i.e., ¼
cu
N
1=m
, then the results of tests on unjointed Khaya indicate a value of the index
m of about 20. However, the value of m reduces to about 16 for scarf-jointed khaya,
poplar and beech, and to about 13 for butt-jointed specimens. Hancock and Bond
(1995) have proposed the use of an index of 13.4 for design purposes for scarf-
jointed wood laminates in gene ral.
Testing at other R (¼
min
=
max
) ratios allows constant life diagrams to be plotted
– see, for example, the diagram for scarf-jointed poplar in Figure 7.8, taken from
0
5
10
15
20
25
30
-60 -50 -40 -30 -20 -10 0 10 20 30 40 50 60 70 80
Mean stress (MPa)
Alternating stress (MPa)
R = -3
R = +3
R = -1 R = -0.84 = UCS/UTS
R = +0.33
10
7
cycles
10
4
cycles
10
5
10
6
UCS UTS
Figure 7.8 Constant Life Diagram for Scarf-Jointed Poplar Derived from 50 percent Median
Regression Lines on S– N Fatigue Test Data
BLADES 391
Bond and Ansell (1998). Note the relatively low stress ranges at R ¼0:84 (¼ UCS/
UTS), which may be due to simultane ous occurrence of compressive and tensile
damage. Despit e this, the simplification of the constant life diagram to a series of
straight lines between the R ¼1 stress range for each fatigue life and either the
UTS or UCS is reasonably accurate.
Material safety factors
The material safety factor applied when timber is used in building construction is
normally high, e.g., about 3–4. Howeve r, there are a number of reasons for
adopting a much lower value in blade design:
(1) laminated construction is used, so any defects are very localized;
(2) the moisture content is carefully controlled during manufacture, and the blade
skin is then very effectively sealed against further moisture ingress;
(3) creep effects are negligible as the gravity loads change direction because of
blade rotation and the wind loads are temporary in nature.
Accordingly a partial safety factor of onl y about 1.5 is normal for design against
extreme loads.
7.1.8 Go verning load cases
Extreme loading during operation: stall-regulated machines
As described in Chapter 5, wind turbine design codes specify a number of load
cases consisting of various combinations of defined wind speed and direction
changes – some of them involving external or machine faults – which are an
attempt to define an envelope of the worst loadings to be expected in practice. It is
instructive to take one such code, IEC 61400-1, and compare the blade loadi ngs
arising from the different load cases for a particular design. The WTG chosen is a
40 m diameter, 500 kW stall-regulated Class II machine fitted with TR blades (see
Figure 5.2(a)) and operating at a single rotational speed of 30 rpm. The rated wind
speed, U
r
, and cut out speed, U
o
, are 16 m/s and 25 m/s respectively. The shaft tilt
with resp ect to the horizontal is taken as 58 so, allowing for a 88 inclination of the
flow to the horizontal as specified in the code, the maximum shaft tilt with respect
to the flow is 138. Category A turbulence characteristics are assumed.
The table below summarizes the conditio ns applicable to the pow er production
load cases (apart from those involving a machine fault) and compares the resulting
peak out-of-plane blade bending moment at 60 percent radius, ignoring dynamic
effects. In the cases involving a change of wind direction, the maximum yaw error
is simply taken as equal to the maximum direction change i.e., ignoring any action
taken by the control system to correct it.
392 COMPONENT DESIGN

Table 7.3 Wind Conditions for Power Production Load Cases for Class IIA 40 m Diameter WTG with 16 m/s Rated Speed and Calculated
Maximum Out-of-plane Bending Moments at 12 m Radius Ignoring Dynamics, for Stall-regulated Machine
Load case Description Hub-height wind speed (m/s)
Initial Gust Max
Wind direction
change ¼ yaw
error
Maximum shaft
tilt with respect
to flow
Maximum
inclination of
flow to shaft axis
Critical blade
azimuth for
maximum
bending
moment
Maximum out-
of-plane
bending
moment at 12 m
radius (kNm)
1.1 Normal turbulence model
– extreme
40.4 278 138 308 258 130
(1.2) (Normal turbulence model
– fatigue)
1.3 Extreme coherent gust with
direction change
16 15 31 458 138 46.88 158 118
1.4 Electrical fault
(not considered)
1.5 Grid loss with 1 year extreme
operating gust
25 11.6 36.6 – 138 138 908 115
1.6 50 year extreme operating gust 25 15.5 40.5 – 138 138 908 108
1.7 Extreme wind shear 25 – 25 – 138 13 8 908 90
1.8 50 year extreme direction change 25 – 25 47.8 138 49.58 158 108
1.9 Extreme coherent gust 16 15 31 – 138 138 908 88
BLADES 393
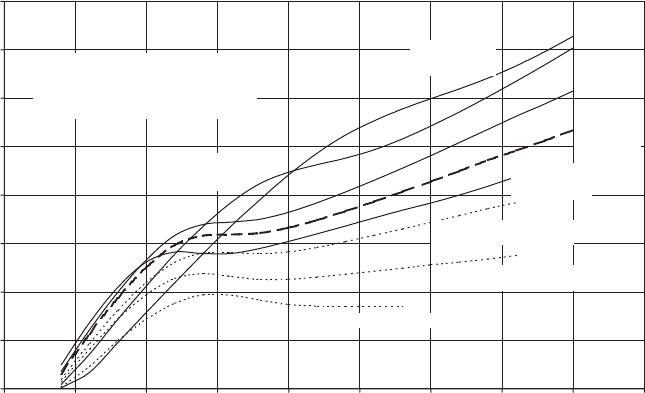
The blade loadings are calculated using empirical three-dimensional aerofoil data
taken from Petersen et al. (1998) – see Figure 5.9. This displays a gentler stall than
typical two-dimensional data, so there is no significant reduction in blade out-of-
plane bending moment as the blade goes into stall. Above about 20 m/s, the out-of-
plane bending moment begins to increase progressively once again as drag begins
to become significant. The predic ted variation of blade 12 m radius out-of-plane
bending moment with wind speed is plotted out for a 0.2 shear exponent and a
range of yaw angles on Figure 7.9, with the yaw direction defined as positive when
the lateral component of air flow with respect to the rotor disc is in the same
direction as the blade movement at zero azimuth (i.e., at 12 o’clock). The effect of
this increase in relative velocity outweighs that of the reduction of angle of attack at
wind speeds beyond stall, so the bending moment at 0 8 azimuth is increased by
negative yaw. Maximum moments occur at negative yaw angles and 08 azimuth
rather than at positive yaw angles and 1808 azimuth, because wind shear augments
the wind speed in the former case . Also plotted is the variation of bending moment
with wind speed for a 138 shaft tilt with respect to flow and 90 8 azimuth, which is
the critical configuration for load cases not involving a change in wind direction.
Considering the deterministic load cases 1.3 and 1.5 to 1.9 initially, it is interesting
to note that the maximum out-of-plane bending moments lie within a relatively close
range in four of the six cases. It sho uld be pointed out that, in the grid-loss case, the
bending moment depends on the rotor acceleration after loss of load, which is largely
determined by rotor inertia and the time delay to tip brake deployment. The bending
moment quoted is a notional one, based on a generous 1.5 s time delay until full
deployment and an inertia value calculated for a fibreglass rotor. With lighter rotors,
0
20
40
60
80
100
120
140
160
0 5 10 15 20 25 30 35 40 45
Wind speed (m/s)
12 m radius out-of-plane bending moment (kNm)
Shear exponent = 0.2
Rotational speed = 30 r.p.m.
Full-line curves are for 0 deg azimuth
⫺40⬚ yaw,
0⬚ azimuth
⫺50⬚ yaw,
0⬚ azimuth
⫺20⬚ yaw,
0⬚ azimuth
0⬚ yaw,
0⬚ azimuth
13⬚ tilt,
90⬚
azimuth
0⬚ yaw, 180⬚ azimuth
⫺20⬚ yaw, 180⬚ azimuth
⫺40⬚ yaw, 180⬚ azimuth
Figure 7.9 Variation of 12 m Radius Out-of-plane Bending Moment with Wind Speed at
Various Yaw Angles for an Example 40 m Diameter Stall-regulated Machine with TR Blades
394
COMPONENT DESIGN
