Burton T. (et. al.) Wind energy Handbook
Подождите немного. Документ загружается.


yaw angle. For 308 of yaw the magnitudes of the measured and calculated tilting
moments are comparable. The measured mean tilting moment is quite definitely
non-zero and positive but the calculated mean moment is much smaller although
still positive. A positive tilt rotation would displace the upper part of the rotor disc
in the downwind direction. In the theory the small mean tilting moment is caused
by the wake rotation velocities.
A theory based upon computational fluid mechanics should provide a much
more accurate prediction of the aerodynamics of a wind turbine in yaw. However,
the severe computational time limitations associated with CFD solutions precludes
their use in favour of the simple theory outlined in these pages.
3.11 The Method of Acceleration Potential
3.11.1 Introduction
An aerodynamic model that is applied to the flight performance of helicopter rotors,
and which can also be applied to wind turbine rotors that are lightly loaded, is that
based upon the idea of acceleration potential. The method allows distributions of
the pressure drop across an actuator disc that are more general than the, strictly,
uniform pressure distribution of the momentum theory. The model has been
expounded by Kinner (1937), insp ired by Prandtl, who has develop ed expressions
for the pressure field in the vicinity of an actuator disc, treating it as a circular wing.
To regard a rotor as a circular wing requires an infinity of very slender blades so
that the solidity remains small.
Kinner’s theory, which is derived from the Euler equations, assumes that the
induced velocities are small compared with the general flow velocity. If u, v and w
are the velocities induced by the actuato r disc in the x-, y- and z-directions,
respectively, and which are very much smaller than the free-stream velocity in the
x-direction U
1
, then the rate of change of momentum in the x-direction of a unit
volume of air will be in response to the pressure gradient in that direction
r (U
1
þ u)
@(U
1
þ u)
@x
þ v
@(U
1
þ u)
@ y
þ w
@(U
1
þ u)
@z
¼
@ p
@x
(3:144)
The free-stream velocity U
1
does not change with position therefore, for example,
@(U
1
)=@x ¼ 0. Also, U
1
(u, v, w) and so, for example , v(@u=@ y) can be ignored
in comparison with U
1
(@u=@x). The mome ntum equation in the x-direction then
simplifies to
rU
1
@u
@x
¼
@ p
@x
(3:145a)
Similarly, in the y- and z-directions, the momentum equations are also simplified
THE METHOD OF ACCELERATION POTENTIAL 125

rU
1
@v
@w
¼
@ p
@ y
(3:145b)
and
rU
1
@w
@x
¼
@ p
@z
(3:145c)
Differentiating each moment um equation with respect to its particular direction
and adding together the results gives
rU
1
@
@x
@u
@x
þ
@v
@ y
þ
@w
@z
¼
@
2
p
@x
2
þ
@
2
p
@ y
2
þ
@
2
p
@z
2
!
but, for continuity of the flow,
@u
@x
þ
@v
@ y
þ
@w
@z
¼ 0,
therefore
@
2
p
@x
2
þ
@
2
p
@ y
2
þ
@
2
p
@z
2
¼ 0(3:146)
which is the Laplace equation governing the pressure field on and surrounding the
actuator disc. Given the boundary conditions at the actuator disc Equation (3.146)
can be solved for the pressure field and, in particular, the pressure distribution at
the disc. The pressure is continuous everywhere except across the disc surfaces
where there is the usual pressure discontinuity, or pressure drop, in the wind
turbine case.
In Coleman’s analysis (1945) the pressure drop distribution across the disc is
uniform (it is only as a result of combining the theory with the blade element theory
that a non-uniform pressure distribution can be achieved) but falls to zero, abrup tly,
at the disc edge. Kinner assumes that the pressure drop is zero at the disc edge and
changes in a continuous manner as radius decreases.
The simplified Euler Equations (3.145) allow pressure to be regarded as the
potential field from which the acceleration field can be obtained, by differentiation,
and thence the velocity field, by integration. Commencing upstream where the
known free-stream conditions apply the velocity components can be determined by
progressive integration towards the disc.
3.11.2 The general pressure distribution theory of Kinner
Kinner’s solution (1937) is mathematically complex and is achieved by means of a
co-ordinate transformation. The Cartesian co-ordinates centred in the rotor plane
126 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES
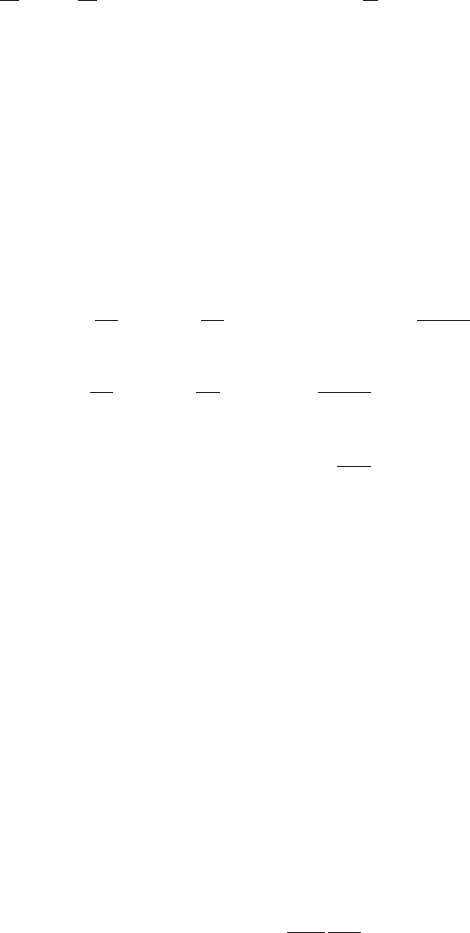
(x}, y
0
, z), as defined in Figure 3.56, are transformed to, what is termed, an
ellipsoidal co-ordinate system (, , ł), ł is the azimuth angle.
x0
R
¼ v,
y9
R
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 v
2
p ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ
2
p
sin ł and
z
R
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 v
2
p ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ
2
p
cos ł (3:147)
On the surface of the rotor disc ¼ 0andr=R ¼ ¼
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 v
2
p
or, conversely,
v ¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2
p
The transformation separates the variables and allows the pressure field to be
expressed as the product of three functions
p(v, , ł) ¼
1
(v)
2
()
3
(ł)(3:148)
each separate function being the solution of a separate, ordinary differential equa-
tion,
d
dv
(1 v
2
)
d
dv
1
(v)
þ n(n þ 1)
m
2
1 v
2
1
(v) ¼ 0(3:149a)
d
d
(1
2
)
d
d
2
()
þ
m
2
1
2
n (n þ 1)
"#
2
() ¼ 0(3:149b)
d
2
dł
2
3
(ł) þ m
2
3
(ł) ¼ 0(3:149c)
where m and n are positive integers.
Equations (3.149a) and (3.149b) have the form of Legendre’s associated differen-
tial equations which has solutions which are called associated Legendre polyno-
mials of the first and second kinds, respectively (see van Bussel, 1995).
If m ¼ 0 then Equations (3.149a) and (3.149b) are reduced to Legendre’s differ-
ential equations the solutions for which are
1
(v) ¼ P
n
(v)(3:150a)
and
1
(v) ¼ Q
n
(v)(3:150b)
where P
n
(v) is a Legendre polynom ial of the first kind and Q
n
() is a Legendre
polynomial of the second kind.
P
n
(v) ¼
1
2
n
n!
d
n
dv
n
(v
2
1)
n
(3:151)
Although the polynomials extend beyond the range v
2
< 1, over that interval the
polynomials are mutually orthogonal
THE METHOD OF ACCELERATION POTENTIAL 127

ð
1
1
P
n
(v)P
k
dv ¼ 0 n 6¼ k (3:152)
For n ¼ 0 the Legendre polynomial of the second kind is
Q
0
(v) ¼
1
2
ln
1 þ v
1 v
(3:153)
For n . 0 the Legendre polynomials of the second kind Q
n
(v) can be obtained from
the polynomials of the first kind. For n ¼ 1to4
Q
1
(v) ¼ (P
1
(v)Q
0
(v)Þ1
Q
2
(v) ¼ (P
2
(v)Q
0
(v)Þ
3
2
v (3:154)
Q
3
(v) ¼ (P
3
(v)Q
0
(v)Þ
5
2
v
2
þ
2
3
Q
4
(v) ¼ (P
4
(v)Q
0
(v)Þ
35
8
v
3
þ
55
24
v
The solutions for Equation (3.149b), with m ¼ 0, are the same as for (3.149a) but
with imaginary arguments, i.e.,
2
() ¼ P
n
(i)(3:155a)
and
2
() ¼ Q
n
(i)(3:155b)
where
Q
0
(i) ¼ i tan
1
() for , 1
and
Q
0
(i) ¼ i
2
tan
1
for . 1
For non-zero values of the integer m the solutions of Equation (3.149a) become
P
m
n
(v) ¼ (1 v
2
)
m=2
d
m
dv
m
P
n
(v)(3:156)
If m . n then P
m
n
(v) ¼ 0.
128 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES
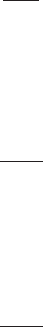
Q
m
n
(v) ¼ (1 v
2
)
m=2
d
m
dv
m
Q
n
(v)
But, from Equation (3.153), Q
m
n
(v) ¼1at v
2
¼ 1 which is physically inapplicable
and so these functions are excluded from the solution.
For solutions of Equation (3.149b) for non-zero values of m
P
m
n
(i) ¼ (1 þ
2
)
m=2
d
m
di
m
P
n
(i)
Inspection reveals that P
m
n
(i) !1as !1which means that pressure would be
infinite in the far field which is not physically acceptable therefore these terms will
also not be included.
Q
m
n
(i) ¼ (1 þ
2
)
m=2
d
m
di
m
Q
n
(i)(3:157)
Equations (3.156) and (3.157) are known as associated Legendre polynom ials.
The solution to differential Equation (3.149c) is more straight forward than for the
other two governing equations
3
(ł) ¼ cos mł, sin mł (3:158)
The complete solution, therefore, for the pressure field surrounding a rotor disc is
p(v, , ł) ¼
X
M
m¼0
X
N
n¼m
P
m
n
(v)Q
m
n
(i)(C
m
n
cos mł þ D
m
n
sin mł)(3:159)
The upper limits M and N can have any positive integer value.
The polynomial Q
m
n
(i) is imaginary for odd values of m and real for even values
therefore the arbitrary constants C
m
n
and D
m
n
must be real or imaginary, accordingly,
in order that the pressure field be real.
Any combination of terms in Equation (3.159) can be used, whatever suits the
conditions. For there to be a pressure discontinuity across the disc, but continuously
varying pressure elsewhere the solutions must be restricted to those for which
n þ m is odd. Of course , limiting the number of terms, other than has been
described, may result in an approximate solution.
The pressure discontinuity across the rotor disc will be as shown in Figure 3.2.
The magnitude of the step in pressure will be twice the pressure level (above the far
field level) that occurs just upstream of the disc. The pressure gradient, however,
normal to the rotor disc, will be continuous.
3.11.3 The axi-symmetric pressure distributions
For the wind turbine rotor disc the simplest situation is for m ¼ 0 which means that
the pressure distribution is axisymmetric. The permitted values of n must be odd.
THE METHOD OF ACCELERATION POTENTIAL 129

For n ¼ 1 the polynom ials are
P
0
1
(v) ¼ v ¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2
p
(3:160a)
and
Q
0
1
(i) ¼ tan
1
1
1(3:160b)
So, on the disc, where ¼ 0, Q
0
1
(i0) ¼1.
Therefore, the pressure distribution is
p( ) ¼C
0
1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2
p
(3:161)
If the pressure in Equation (3.161) is non-dimensionalized using the free-stream
dynamic pressure (1=2)rU
2
1
the value of C
0
1
can be related to the thrust coefficient
by integrating the pressure distribution of Equation (3.161) over the disc area
R
2
C
T
¼R
2
C
0
1
ð
2
0
ð
1
0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2
p
d d ł ¼
2
3
R
2
C
0
1
Therefore,
C
0
1
¼
3
2
C
T
(3:162)
and so the pressure step across the disc is
p
1
( ) ¼ C
T
3
2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2
p
(3:163)
All the remaining polynomials (for m ¼ 0 and odd values of n . 1) produce zero
thrust. To modify the pressure distribution to suit the boundary conditions an
appropriate linear combination of solutions can be added to that of Equation
(3.163).
The application to helicopter rotors leads to a requirement for the pressure and
the radial pressure gradient to be zero at the rotor axis as these conditions corre-
spond to the pressure on actual rotors. The above pressure distribution does not
have zero pressure at the rotor axis and so needs to be combined with at least one
other solution. The second axisymmetric solution, n ¼ 3, is
P
0
3
(v) ¼
1
2
v(5v
2
3) ¼
1
2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2
p
(2 5
2
)(3:164a)
and
Q
0
3
(i) ¼
2
(5
2
þ 3) tan
1
1
þ
5
2
2
þ
2
3
,soQ
0
3
(i0) ¼
2
3
(3:164b)
130 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

The second pressure distribution is, therefore,
p
2
( ) ¼
1
3
C
0
3
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2
p
(2 5
2
)(3:165)
The sum of the two pressure distributions must be zero where ¼ 0, so
C
0
3
¼
9
4
C
T
and the combi nation of the two distributions is
p
12
( ) ¼
15
4
C
T
2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2
p
(3:166)
The three distributions are shown in Figure 3.71.
As most modern wind turbines are designed to achieve as uniform a pressure
distribution as practicable, to maximiz e efficiency, the form chosen for the helicop-
ter rotor might need to be modified. A uniform pressure distribution can be formed
by combining solutions but, because the pressure discontinuity must itself be
discontinuous at the disc edge, it would mean that a great many solutions would be
required. Tip-loss effects would require zero pressure at both the blade tips and at
the hub but for most of the blade span the pressure should be uniform. It should be
pointed out that the blade loading caused by uniform pressure does increase linearly
with radius.
The induced velocity field caused by the axisymmetric pressure distribution has
to be obtained from the pressure field by integrating Equations (3.145) commencing
far upstream where free-stream conditions are assumed to apply. The upstream
1.5
1.0
0.5
0.0
-0.5
-1.0
0 0.2 0.4 0.6 0.8 1
µ
p
1
(µ)
p
2
(µ)
p
12
(µ)
Figure 3.71 Radial Pressure Distributions of the First Two Solutions and their Combination
to Satisfy the Requirements at the Rotor Axis
THE METHOD OF ACCELERATION POTENTIAL 131
conditions also depend upon the angle of yaw of the disc. The integration continues
until a point on the disc is reached where the induced velocity is to be determined.
The particular induced velocity component that is most important for determin-
ing the angle of attack on a blade element is normal to the rotor disc, i.e., the axial
induced velocity. Mangler and Squire (1950) calculated the axial induced velocity
distribution as a function of yaw angle by expressing the velocity as a Fourier series
of the azimuth angle ł.
u
U
1
¼ C
T
A
0
( , ª)
2
þ
X
1
k¼1
A
k
( , )sin kł
!
(3:167)
For the pressure distribution of Equation (3.166) the Fourier coefficients are
A
0
( , ª) ¼
15
8
2
(1
2
)
1=2
(3:168a)
A
1
( , ª) ¼
15
256
(9
2
4)tan
ª
2
(3:168b)
A
3
( , ª) ¼
45
256
3
tan
ª
2
3
(3:168c)
Higher-order odd terms are zero. There are also even terms which have the general
form
A
k
¼ (1)
(k2)=2
3
4
k þ v
k
2
1
9v
2
þ k
2
6
k
2
9
þ
3v
k
2
9
1 v
1 þ v
k=2
tan
ª
2
k=2
where v
2
¼ 1
2
and k is an even integer greater than zero.
The average val ue of the axial induced flow factor is independent of yaw angle
and is given by
a
0
¼
u
0
U
1
¼
1
4
C
T
where u
0
is the average axial induced velocity.
Thus, the average value of the axial flow induced flow factor is related to the
thrust coefficient by
C
T
¼ 4a
0
(3:169)
compared with the momentum theory C
T
¼ 4a
0
(1 a
0
) or compared with any of
the expressions developed for yawed conditions (Equations (3.91), (3.106) and
(3.112)).
Because of the assumption that the induced velocity is small compared with the
flow velocity, a
0
is small compared with 1. Clearly, the acceleration potential
method only appl ies if the value of C
T
is much less than 1.
132 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

The once per revolution term in Equation (3.167) will cause an angle of attack
variation and, hence, a lift variation that will cause a yawing moment on the disc.
However, the pressure distribution, being axi-symmetric, cannot cause a yawing
moment. The situation is much the same as for the vortex theory of Coleman,
Feingold and Stempin (1945).
Pitt and Peters (1981) use, or rather, impose Glauert’s assumption (Equation
(3.108)) for the variation of the axial induced flow factor:
a ¼ a
0
þ a
S
sin ł (3:170)
The value of a
S
is obtained by equating the first moment about the yaw axis of
Equation (3.170) with the first moment of Equation (3.167) using the Mangler and
Squire velocity distributions of Equations (3.168).
ð
2
0
ð
1
0
sin ł(a
0
þ a
S
sin ł)2 d dł
¼
ð
2
0
ð
1
0
sin łC
T
A
0
(, ª)
2
þ
X
1
k¼1
A
k
( , ª)sin kł
!
d d ł (3:171)
All terms, apart from that co ntaining A
1
, vanish on integration, giving
a
S
¼
15
128
tan
ª
2
C
T
(3:172)
Hence, using Equation (3.169), the axial induced velocity becomes
a ¼ a
0
1 þ
15
32
tan
ª
2
sin ł
(3:173)
Which, apart from the use of the yaw angle instead of the wake skew angle, has the
same form as Equations (3.108) and (3.118) and so there is some consistency in the
various methods for dealing with yawed flow.
3.11.4 The anti-symmetric pressure distributions
As has been determined in Section 3.10.11, there is a moment about the vertical
diameter of a yawed wind turbine rotor disc, the restoring yaw moment. An axi-
symmetric pressure distr ibution, however, is not capable of producing a yaw
moment and so more terms from the series solution of Equation (3.159) need to be
included.
The only terms in Equation (3.159) which wil l yield a yawing moment are those
for which m ¼ 1 and for which D
1
n
6¼ 0. Terms for which m ¼ 1 and C
1
n
6¼ 0 will
cause a tilting moment. Recalling that m þ n must be odd to achieve a pressure
discontinuity across the disc the values of n that may be combined with m ¼ 1 must
be even.
THE METHOD OF ACCELERATION POTENTIAL 133

Because of the nature of the Legendre polynomials only one term in the series of
Equation (3.159) will produce a net thrust and only one term will produce a yawing
moment, which is a first moment. Similarly only one term will produce a second
moment, and so on.
The unique term in Equation (3.159) which yields a yawing moment is that for
which m ¼ 1, n ¼ 2 and C
1
n
6¼ 0, therefore
P
1
2
(v) ¼ 3v
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 v
2
p
¼ 3
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2
p
(3:174)
and
Q
1
2
(i) ¼ 3i
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ
2
p
tan
1
1
3i
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ
2
p
þ
i
ffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ
2
p
,(3:175)
so
Q
1
2
(i0) ¼2i (3:175a)
A zero pressure gradient at the rotor axis is not appropriate in this case because the
pressure distribution is anti-symmetric about the yaw axis, therefore,
p( , ł) ¼ P
1
2
( )Q
1
2
(i0)D
1
2
sin ł ¼6iD
1
2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
2
p
sin ł (3:176)
The pressure distribution is shown in Figure 3.72.
The yawing moment coefficient is defined by
C
mz
¼
M
z
1
2
rU
2
1
R
3
(3:177)
As before, if the pressure in Equation (3.176) is non-dimensionalized by the free-
stream dynamic pressure (1=2)rU
2
1
, then
ψ
Figure 3.72 The Form of the Pressure Distribution which Yields a Yawing Moment
134
AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES
