Burton T. (et. al.) Wind energy Handbook

Подождите немного. Документ загружается.

analysis of Section 3.4. The vorticity g

has a direction which remains parallel to the

yawed disc and assuming it to be uniform (not varying with the azimuth angle),

using the Biot–Savart law, induces an average velocity at the disc of aU

sec =2ina

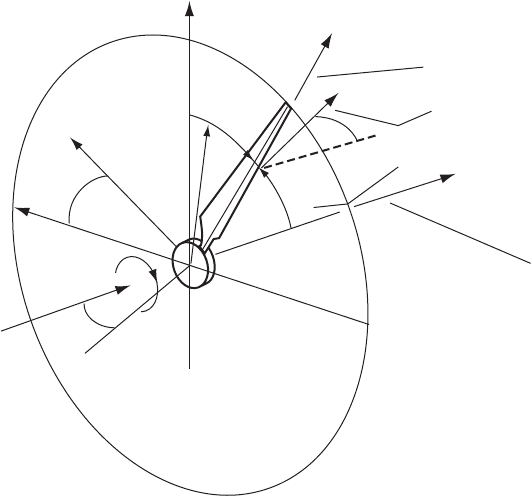
direction which bisects the skew angle between the central axis of the skew angle,

as shown in Figure 3.54. The average axial induced velocity, normal to the rotor

plane, is aU

, as in the unyawed case. In the fully developed wake the induced

velocity is twice that at the rotor disc.

Because the average induced velocity at the disc is not in the rotor’s axial

direction, as is assumed for the momentum theory of Sections 3.10.1 and 3.10.2, the

force F on the disc, which must be in the axial direction, cannot be solely res-

ponsible for the overall rate of change of momentum of the ﬂow; there is a change

of momentum in a direction normal to the rotor axis.

The velocity components at the rotor disc deﬁne the skew angle:

tan  ¼

sin ª  a tan





(cos ª  a)

2 tan



1  tan



(3:109)

From which it can be shown that a close, appr oximate relationship between , ª

and a is

 ¼ (0:6a þ 1)ª (3:110)

Using the velocities shown in Figure 3.54 a fresh analysi s can be made of the ﬂow.

The average force on the disc can be determined by applying Bernoulli’s equation

to both the upwind and downwind regions of the ﬂow.

Upwind

¼ p

a sec

Figure 3.54 Average Induced Velocities Caused by a Yawed Actuator Disc

THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 105

Downwind



¼ p

(cos ª  2a)

þ sin ª  2a tan





where U

is the resultant velocity at the disc.

Subtracting the two equations to obtain the pressure drop across the disc

 p



4a cos ª þ tan



sin ª  a sec





The coefﬁcient of thrust on the disc is therefore,

¼ 4a cos ª þ tan



sin ª  a sec





(3:111)

and the power coefﬁcient is

¼ 4a cos ª þ tan



sin ª  a sec





(cos ª  a)(3:112)

In a similar manner to the Glau ert theory, it is not clear how much of the thrust in

Equation (3.111) is capable of extracting energy from the ﬂow and so the expression

for power in Equation (3.112) will probably be an over estimate. A comparison of

the maximum C

values derived from the three theories, as a function of the yaw

angle, is shown in Figure 3.55.

0.6

0.4

0.2

Glauert momentum

Vo r t e x

Axial momentum

max

0 20 40 60 80

Yaw an

(

rees

)

Figure 3.55 Maximum Power Coefﬁcient Variation with Yaw Angle, Comparison of Mo-

mentum and Vortex Theories

106

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

3.10.4 Flow expansion

The induced velocity component parallel to the skewed axis of the wake is uniform

over the disc with a value aU

, as can be deduced from Figure 3.54. The induced

horizontal velocity, normal to the skewed axis of the wake is also uniform over the

area of the disc with a value a tan(=2)U

In addition to the uniform induced velocities of Figure 3.54 the expansion of the

ﬂow gives rise to velocities in the y and z directions, respectively (i.e., directions in

a vertical plane at the skew angle  to the rotor plane, see Figure 3.56). When

resolved into the rotor plane the ﬂow expansion velocities will give rise to a normal

induced velocity of the type predicted by Glau ert in Equation (3.108).

At a point on the disc at radius r and azimuth angle Ł, deﬁned in Figure 3.56,

the induced ﬂow expansion velocities are non-simple functions of r and Ł. Across

the horizontal diameter, where Ł ¼908, Coleman et al. (1945) obtained an

analytical solutio n for the ﬂow expansion velocity in the y direction that involves

complete elliptic integrals; the solution is not very practicable because numerical

evaluation requires calculating the difference between two large numbers. Simpli-

ﬁcation of the analytical solution leads to the following expression for the

horizontal ﬂow expansion velocity which removes that difﬁculty but it is not in

closed form.

z,w

y,v

y'',v''

x'', u''

z'', w''

Radially along the blade

Normal to the rotor plane

Tangentially in the rotor plane

Axis of the skewed wake

x,u

Ω

Figure 3.56 Axis System for a Yawed Rotor

THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 107

(, ) ¼

2 sin ŁaU



sin

2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

(1 þ )

 4 sin



[(  þ cos 2)

]cos

 þ sin

2

d (3:113)

where  ¼ r=R,  is a parameter arising from the elliptic integrals, which is elimi-

nated from the function by the deﬁnite integral, and aU

is the average induced

velocity as previously deﬁned. An important feature of Equation (3.113) is that the

ﬂow expansion velocity is proportional to the average axial ﬂow induction factor.

Furthermore, if Equation (3.113) is divided by sec(=2)

the result is almost

independent of the skew angle . Let

(, )

sec



sin ł aU

be deﬁned as the ﬂow expansion function F( ) which is shown in Figure 3.57,

clearly demonstrating how little F( ) changes over a range of skew angle of 08 to

608.

At all skew angles the value of the ﬂow expansion function is inﬁnite at the edge

of the rotor disc, indicating a singularity in the ﬂow which, of course, does not

occur in practice but is a result of assuming uniform blade circulation. Circulation

must fall to zero at the disc edge in a smooth fashion.

No analytical expressions for the ﬂow expansion velocity components for values

of Ł other than 908 were developed by Coleman et al. (1945) but numerical

evaluations of the ﬂow expansion velocities can be made using the Biot–Savart law.

The radial variatio n of the vertical ﬂow expansion velocity across the vertical

diameter of the rotor disc is much the same as F( ) for skew angles between 458

but outside of this range the vertical velocity increases more sharply than the

horizontal velocity at the disc edge. As will be shown, the vertical expansion

0.5

60°

30°

0°

0.2

0.4

0.6

0.8

F(µ)

Figure 3.57 Flow Expansion Function Variation with Radial Position and Skew Angle

108

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

velocity is of less importance than the horizontal velocity in determining the

aerodynamic behaviour of the yawed rotor.

The variation of the horizontal and vertical ﬂow expansion velocities along radial

lines on the rotor disc surface at varying azimuth angles (a radius sweeping out the

disc surface as it rotates about the yawed rotor axis) shows that some further sim-

pliﬁcations can be made for small skew angles.

Figure 3.58 shows the variation of the ﬂow expansion velocities across the rotor

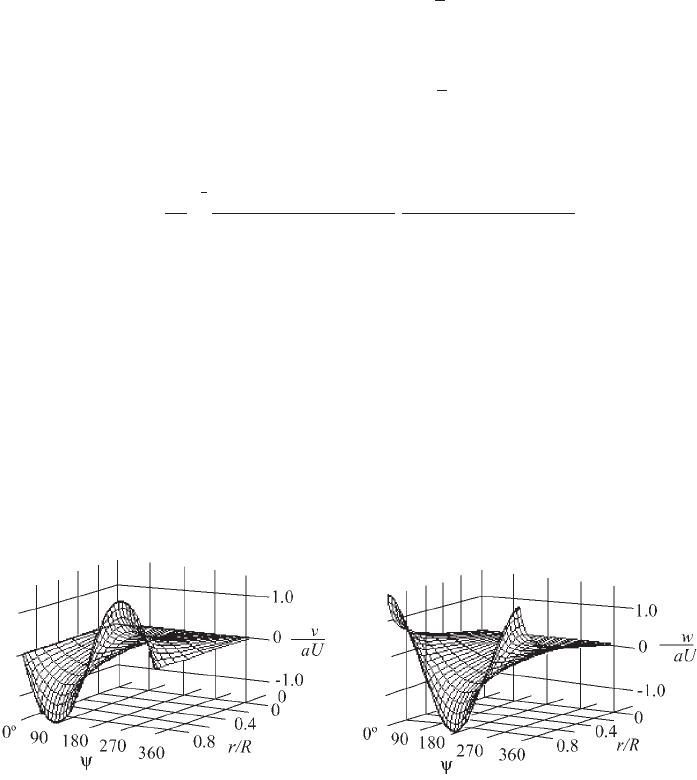
disc for a skew angle of 308. It should be emphasized that the velocity components

lie in planes that are normal to the skewed axis of the wake. Inspection of the

variations leads to simple approximations for the two velocity components.

(, , ł) ¼ aU

F( )sec



sin ł (3:114)

w(, , ł) ¼ aU

F( )sec



sin ł (3: 115)

where

F( ) ¼

2



sin

2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

(1 þ )

 4 sin



( 

þ 2 cos(2 þ 1)

d (3:116)

The drawback of Equations (3.114) and (3.115) is the sin gularity in the ﬂow

expansion function (3.116) at the outer edge of the disc. If the actuator disc is

replaced with a rotor which has a small number of blades then the ﬂow expansion

function changes very signiﬁc antly. Conducting a calculation using the Biot–Savart

law for a non-yawed, single-bladed rotor represented by a lifting line vortex of

radially uniform strength the ﬂow expansion function can be determined numeri-

cally. It is found that the ﬂow expansion velocity along the radial lifting line is a

function of the helix (ﬂow) angle of the discrete line vortex shed from the tip of the

lifting line (blade). The vortex wake is assumed to be rigid in that the helix angle

and the wake diameter are ﬁxed everywhere at the values which pertain at the

rotor. The solutions for a single-blade rotor can be used to determine the ﬂow ﬁelds

Figure 3.58 Azimuthal and Radial Variation of Horizontal (v) and Vertical (w) Velocities on

the Rotor Plane for a Skew Angle of 308

THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 109

for multi-blade rotors by a simple process of superposition. The resulting ﬂow

expansion functions F()

are depicted in Figure 3.59 for one-, two- and three-blade

rotors.

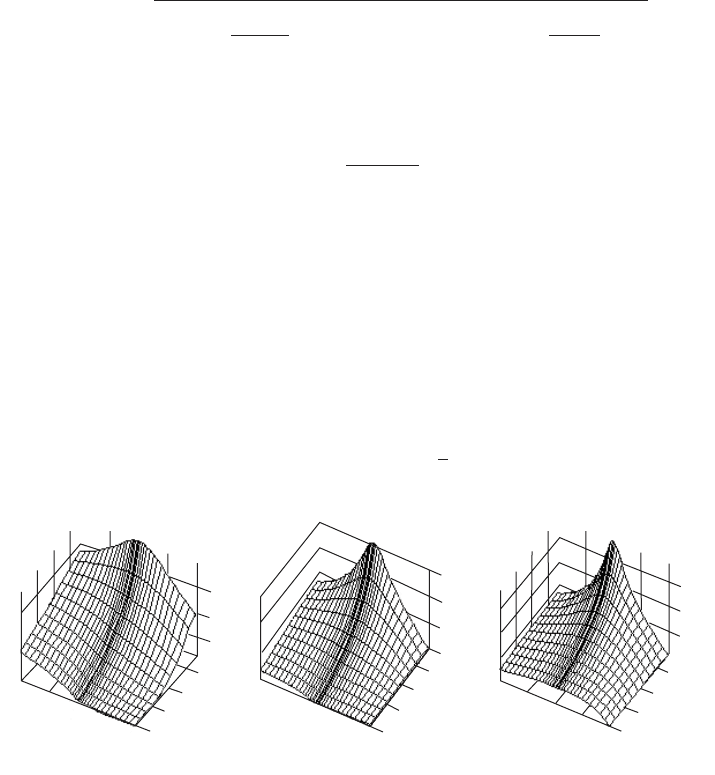
The radial variations in Figure 3.59 have been extended beyond the rotor radius

to show the continuity which exists for the discrete blade situation as compared

with the singularity that occurs for the actuator disc. There are two striking features

of the ﬂow expansion functions of Figure 3.59: the function is heavily modiﬁed by

the value of the helix angle  and the negative values (ﬂow contraction) that can

occur for the single-blade rotor.

An analytical expression which approximates the form of the diagrams shown in

Figure 3.59 for two- and three-bladed rotors is

( , 

, N) ¼

F( )

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 þ 50

tan



F( )

(F( )(2  ))

0:05=tan 

tan 

þ 8



(3:117)

where

k ¼

1  a

º(1 þ a9 )

is the tangent of the ﬂow angle at which the tip vortex is shed from the blade tips.

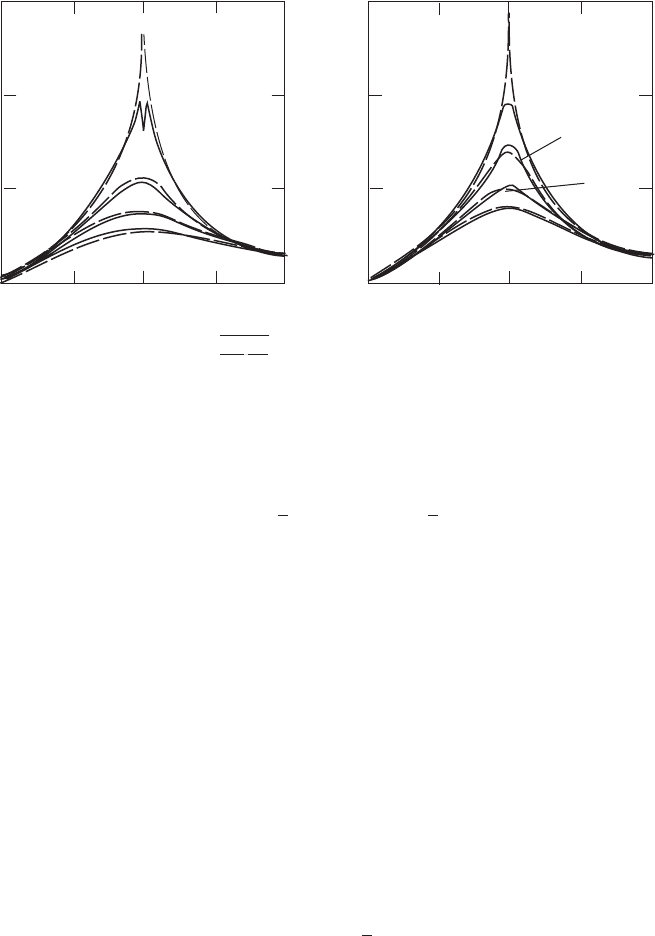
The approximation of Equation (3.117) is shown in Figure 3.60 for two- and three-

bladed rotors.

When transformed as components of velocity with respect to axes rotating about

the rotor axis (x", y" and z" axes as shown in Figure 3.56) the ﬂow expansion

velocities of Equations (3.114) and (3.116) are resolved into the components that are

normal and tange ntial to the blade element (see Figure 3.63).

The normal co mponent is

u0 ¼ aU

1 þ F( )2 tan



sin ł



(3:118)

0.6

0.4

0.2

0.25

0.5

0.75

1.0

Three blades

0.6

0.4

0.2

0.25

0.5

0.75

1.0

0.2

-0.2

0.25

0.5

0.75

1.0

tan (ψ)

F(µ)

tan (ψ)

One blade Two blades

Figure 3.59 Flow Expansion Functions for One-, Two- and Three-blade Rotors

110

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

And the tangential component is

v 0 ¼ aU

cos ł tan



1 þ F( )2 tan



sin ł



(3:119)

to which must be added the components of the wind velocity U

the normal component

U0 ¼ cos ª U

(3:120)

and the tangential component

V ¼ cos ł sin ª U

(3:121)

There is a radial (span-wise) velocity component but this will not inﬂuence the

angle of attac k so can be ignored.

Clearly, from Equation (3.118), the Coleman theory determines the function K(),

see equation 3.108, as being

() ¼ 2 tan



(3:122)

In addition there is the tangential velocity r caused by blade rotation and also the

induced wake rotation but the latter will be ignored initially.

The velocities of Equations (3.118) to (3.121) will produce a lower angle of attack

when the azimuth angle ł is positive, see Figure 3.57, than wh en it is negative and

so the angle of attack will vary cyclically. When ł is positive the incident normal

velocity u} lies closer to the radial axis of the blade than when ł is negative. The

0 0.5 1 1.5 2

Two blades

1.5

0.5

1.5

0.5

Flow expansion function

Three blades

k = 0.01

k = 0.1

k = 0.2

k = 0.3

k = 0.1

k = 0.2

k = 0.3

k = 0.01

Approximate

Exact

r/R

Figure 3.60 Approximate Flow Expansion Functions for Two- and Three-blade Rotors

THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 111

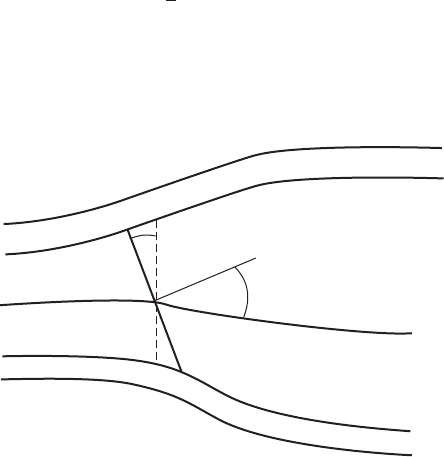
difference in angle of attack can be attributed to ﬂow expansion as depicted in

Figure 3.61.

The variation of the angle of attack makes the ﬂow ab out a blade aerofoil

unsteady and so the lift will have a response of the kind discussed in Section 3.1.

The blade circulation will therefore vary during the course of a revolution, which

means that the vortex model is incomplete because it is derived from the assump-

tion that the circulation is constant.

There is clearly additional vorticity in the wake being shed from the blades’

trailing edges inﬂuencing the induced velocity, which is not accounted for in the

theory. The additional induced velocity would be cyclic so would probably not

affect the average induced velocity normal to the rotor disc but would affect the

amplitude and phasing of the angle of attack.

Further numerical analysis of the Coleman vortex theory reveals that at skew

angles greater than 458 higher harmonics than just the one per revolution term in

Equation (3.108) become signiﬁcant in the ﬂow expansion induced velocities. Only

odd harmonics are present, reﬂecting the anti-symmetry about the yaw axis.

3.10.5 Related theories

A numb er of reﬁnements to the Glauert and Coleman theories have been proposed

by other researchers, mostly addressing helicopter aerodynamics but some have

been directed speciﬁcally at wind turbines. In particular, Øye (1992) undertook the

same analysis as Coleman and proposed a simple curve-ﬁt to Equation (3.116)



( ) ¼

(  þ 0:4

þ 0:4

)(3:123)

Øye has clearly avoided the very large values that Equation (3.116) produces

close to the outer edge of the disc and Equation (3.122) is in general accordance with

the ﬂow expansion functions shown in Figure 3.59.

High angle of attack

Low angle of attack

Figure 3.61 Flow Expansion Causes a Differential Angle of Attack

112

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

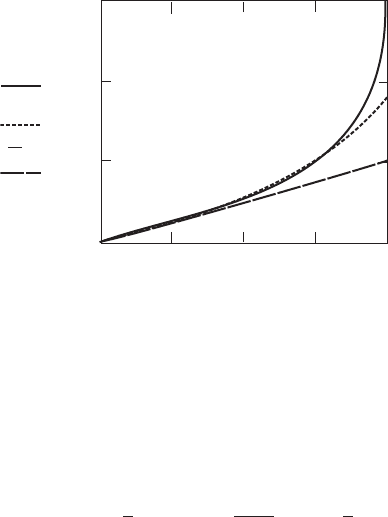
Meijer Drees (1949) has extended the Coleman et al. vortex model to include a

cosinusoidal variation of blade circulation. The main result is a mod iﬁcation to the

function K() but Meijer-Drees retained Glauert’s assumption of linear variation of

normal induced velocity with radius

u0 ¼aU

1 þ

 1  1 :8

sin ª



tan



sin ł

()

(3:124)

(see Schepers and Snel, 1995).

3.10.6 Wake rotation for a turbine rotor in steady yaw

Wake rotation is, of course, present in the wake ﬂow but cannot be related only to

the torque. The vortex theory needs also to include a root vortex, which will lie in

the wake along the skewed wake axis. The rotation in the wake will therefore be

about the skewed wake axis and not about the axis of rotation and the wake rotation

velocity will lie in a plane normal to the skewed wake axis.

To determine the wake rotation velocity the rate of change of angular momentum

about the skewed wake axis will be equated to the moment about the axis produced

by blade forces.

If the wake rotation velocity is described, as before, in terms of the angular

velocity of the rotor then

v - ¼ r-a9h(ł)(3:125)

where the triple prime denotes an axis system rotating about the wake axis and h( Ł)

is a function which determines the intensity of the root vortex’s inﬂuence. In the

non-yawed case the root vortex induces a velocity at the rotor which is half of that it

induces in the far wake at the same radial distance and the same would apply to a

disc no rmal to the skewed axis with a centre located at the same position as the

1.5

0.5

0 0.25 0.5 0.75 1

(µ)

Figure 3.62 Øye’s Curve-ﬁt to Coleman’s Flow Expansion Function

THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 113

actual rotor disc. The distance upstream or downstream of a point on the actual

rotor disc from the plane of the disc normal to the wake axis determines the value

of the root vortex inﬂuence function h(ł). The value of h(ł) will lie between 0.0 and

2.0, being equal to 1.0 at points on the vertical diameter.

The velocity induced by a semi-inﬁnite line vortex of strength ˆ lying along the x-

axis from zero to inﬁnity at a point with cylindrical co-ordinates (x- , ł-, r-) is,

using the Biot–Savart law,

!

V - ¼

4r-

1 þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ r-



v -

(3:126)

The induced velocity when x- ¼1is twice that when x- ¼ 0 and is zero when

x- ¼1.

For a point on the rotor disc (0, ł, r) the corresponding co-ordinates (x-, ł -, r -)

in normal disc axes are

x- ¼y- sin  ¼ r sin ł sin , r- ¼ r

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

cos ł

þ cos 

sin ł

and

cos ł- ¼

cos ł, sin ł- ¼

sin ł cos  (3:127)

the induced velocity at the same point is

v - ¼ r-a9 1 þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ r-



(3:128)

So, transforming the velocity of (3.126) to the rotating axes in the plane of the rotor

disc

!

V 0 ¼

10 0

0cosł sin ł

0 sin ł cos ł

cos  sin  0

sin  cos  0

001

10 0

0 cos ł- sin ł-

0 sin ł- cos ł-

v -

(3:129)

Substituting (3.127) and (3.128) into (3.129) gives

!

V 0 ¼

cos ł sin 

cos 

ra9(1 þ sin ł sin )(3:130)

114 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES