Burton T. (et. al.) Wind energy Handbook

Подождите немного. Документ загружается.

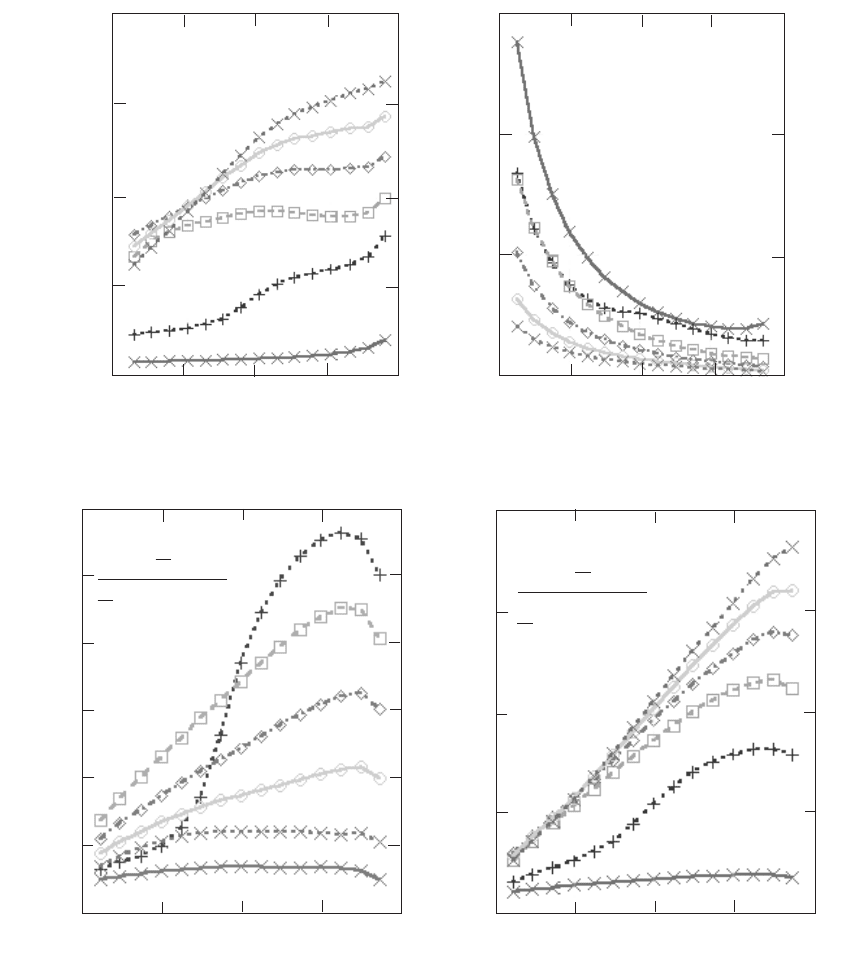
the ﬂat distribution of torque at the high tip speed ratio of 12; this is caused by the

effect of drag which reduces torque as the square of the local speed ratio and with

the low angle of attack at º ¼ 12 drag causes a signiﬁcant loss of power.

Although the blade axial force coefﬁcient increases with tip speed ratio it must be

0.8

0.6

0.4

0.2

0.2 0.4 0.6 0.8 1

r/R

0.15

0.1

0.05

Tangential flow induction factor

Axial flow induction factor

Figure 3.43 Distribution of the Flow Induction Factors for a Range of Tip Speed Ratios

0.6

0.5

0.4

0.3

0.2

0.1

0.2 0.4 0.6 0.8 1

r/R

Torque per unit span

p U

s R

p U

s R

0.2 0.4 0.6 0.8 1

r/R

Blade axial force per unit span

Figure 3.44 Distribution of Blade Loads for a Range of Tip Speed Ratios

CALCULATED RESULTS FOR AN ACTUAL TURBINE 95

remembered that the actual thrust force increases with wind speed as is demon-

strated in Figure 3.45.

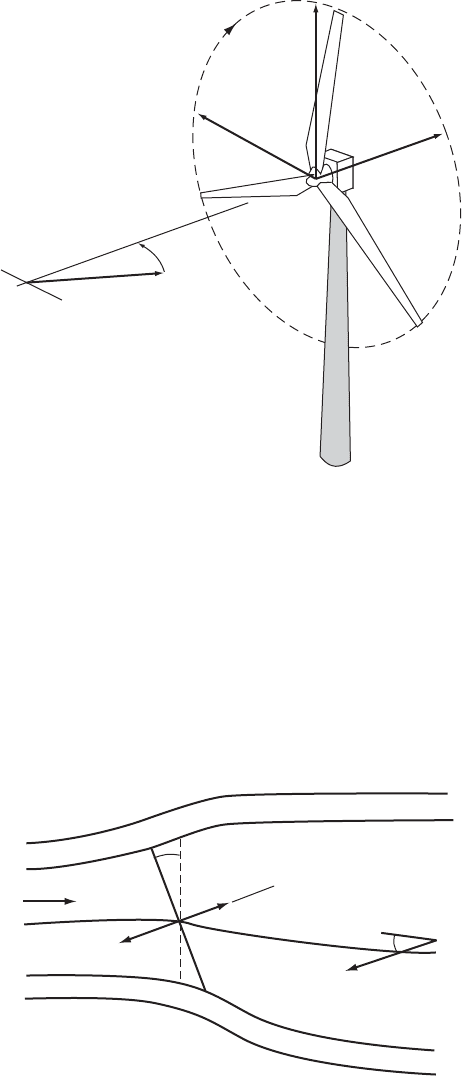
3.10 The Aerodynamics of a Wind Turbine in Steady

Yaw

The rotor axis of a wind turbine rotor is usually not aligned with the wind because

the wind is continuously changing direction; the rotor is not capable of following

this variability and so spends most of its time in a yawed condition. The yawed

rotor is less efﬁcient than the non- yawed rotor and so it is vital to assess the

efﬁciency for purposes of energy production estimation.

In the yawed condition, even in a steady wind, the angle of attack on each blade

is continuously changing as it rotates and so the loads on the rotor blades are

ﬂuctuating, causing fatigue damage. The changes in angle of attack mean that the

blade forces cause not only a thrust in the axial direction but also moments about

the yaw (z) axis and the tilt axis.

Even if the rotor is operating with a uniform induced velocity over the rotor disc

when aligned with a steady wind, once the rotor is misaligned the induced velocity

varies both azimuthally and radially which makes its determination much more

difﬁcult (Figure 3.46).

3.10.1 Momentum theory for a turbine rotor in steady yaw

The application of the momentum theory to an actuator disc representing a yawed

rotor is somewhat problematical. The momentum theory is only capabl e of deter-

mining an average induced velocity for the whole rotor disc but, although in the

non-yawed case the restriction was relaxed to allow some radial variation, it would

not be appropriate to do this in the yawed case because the blade circulation is also

changing with azimuth position. If it is assumed that the force on the rotor disc,

Axial force coefficient

1.5

0.5

0 5 10 15

Tip speed ratio

0 5 10 15 20 25 30

Wind speed (m/s)

Axial force (kN)

Figure 3.45 Axial Force Coefﬁcient and the Variation of the Actual Force with Wind Speed

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

which is a pressure force and so normal to the disc, is responsible for the rate of

change of momentum of the ﬂow then the average induced velocity must also be in

a direction at right angles to the disc plane, i.e., in the axial direction. The wake is

therefore deﬂected to one side because a component of the induced velocity is at

right angles to the wind direction. As in the non-yawed case the average induced

velocity at the disc is half that in the wake.

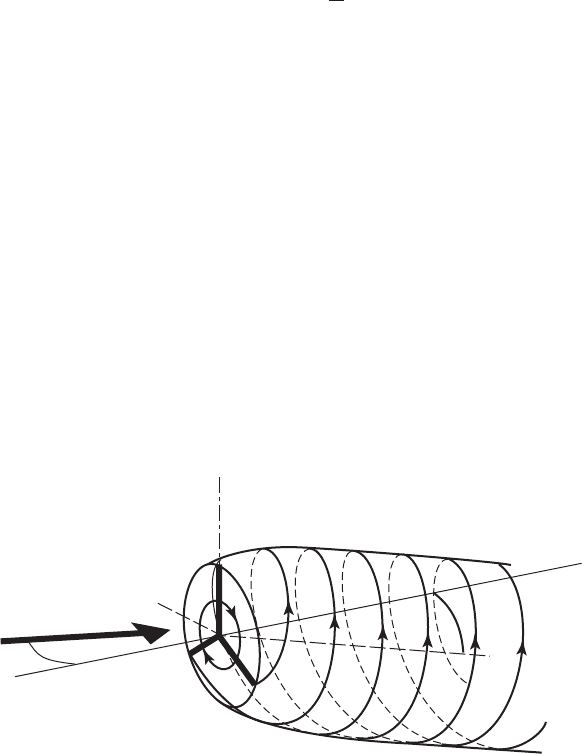
Let the rotor axis be held at an angle of yaw ª to the steady wind direction

(Figure 3.47) then, assuming that the rate of change of momentum in the axial

Figure 3.46 A Wind Turbine Yawed to the Wind Direction

2aU

F= ρ A

(cos(

γ – α) 2 a U

Figure 3.47 Deﬂected Wake of a Yawed Turbine and Induced Velocities

THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 97

direction is equal to the mass ﬂow rate through the rotor disc times the change in

velocity normal to the plane of the rotor

F ¼ rA

(cos ª  a)2aU

(3:88)

Therefore the thrust coefﬁcient is

¼ 4a(cos ª  a)(3:89)

and the power developed is

(cos ª  a)

¼ 4a(cos ª  a)

(3:90)

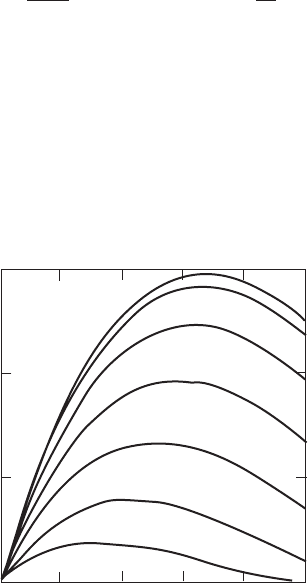
Figure 3.48 shows the decrease in power as the yaw angle increases.

To ﬁnd the maximum value of C

differentiate Equation (3.90) with respect to a

and set equal to zero, whence

a ¼

cos ª

and C

max

cos

ª (3:91)

This cos

ª rule is commonly adopted for power assessment in yawed ﬂow.

A question remains: is it legitimate to apply the momentum theory in the above

manner to the yawed rotor? Transverse pressure gradients whic h cause the wake to

skew sideways may well also contribute to the net force on the ﬂow in the axial

direction, inﬂuencing the axial induced velocity. The above analysis might be

satisfactory for determining the average axial induced velocity but there is even less

justiﬁcation to apply the momentum theory to each blade element position than

there is in the non-yawed case. If a theory is going to be of any use in design it must

0.6

0.4

0.2

0 0.1 0.2 0.3 0.4 0.5

Figure 3.48 Power Coefﬁcient Variation with Yaw Angle and Axial Flow Factor

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

be capable of determining the induced velocity at each blade element position to a

satisfactory accuracy. The sati sfactory calculation of blade forces is as important as

the estimation of power.

3.10.2 Glauert’s momentum theory for the yawed rotor

Glauert (1926) was primarily interested in the autogyro which is an aircraft with a

rotor to provide lift and a conventional propeller to provide forward thr ust. The

lifting rotor has a rotati onal axis which inclines backwards from the vertical and by

virtue of the forward speed of the aircraft air ﬂows through the rotor disc causing it

to rotate and to provide an upward thrust. Thus, the autogyro rotor is just like a

wind turbine rotor in yaw, when in forward ﬂight. At high forward speeds the yaw

angle is large but in a power off vertical descent the yaw angle is zero.

Glauert maintained that at high forward speed the rotor disc, which is operating

at a high tip speed ratio, is like a wing of circular plan-form at a small angle of

attack (large yaw angle) and so the thrust on the disc is the lift on the circular wing.

Simple lifting line wing theory (see Prandtl and Tietjens, 1957) states that the down-

wash (induced velocity) at the wing, caused by the trailing vortex system, is

uniform over the wing span (transverse diameter of the disc) for a wing with an

elliptical plan-form and this would include the circular plan-form of the aut ogyro

rotor.

The theory gives the uniform (average) induced v elocity as

u ¼

(2R)

(3:92)

where L is the lift and V is the forward speed of the aircraft.

The lift is in a direction normal to the effective incident velocity W (see Figure

3.49) and so is not vertical but leans backwards. The vertical component of the lift

Velocities

Drag

-Mg

Lift

Forces

Lift

Figure 3.49 Velocities and Forces on an Autogyro in Fast Forward Flight

THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 99

supports the weight of the aircraft and the horizontal component constitutes drag.

In horizontal ﬂight the vertical component of the lift does no work but the drag

does do work.

The vector triangles of Figure 3.49 show that

(3:93)

In the wake of the aircraft the induced velocity u

caused by the trailing vortices

is greater than that at the rotor. A certain mass ﬂow rate of air, rVS, where S is an

area, normal to velocity V, yet to be determined, undergoes a downward change in

velocity u

in the far wake. By the momentum theory the rate of change of

downward momentum is equal to the lift, therefore

L ¼ rVSu

(3:94)

The rate of work done by the drag DV must be equal to the rate at which kinetic

energy is created in the wake

VS, because the ambient static pressure in the

wake of the aircraft is the same as the pressure ahead of the aircraft.

DV ¼

VS (3:95)

Combining Equations (3.93), (3.94) and (3.95) gives

D ¼

2rV

(3:96)

and

¼ 2u (3:97)

Equation (3.97) should look familiar. Combining Equation (3.92), the lifting line

theory’s assessment of the induced velocity at the rotor, with Equation (3.93) gives

D ¼

(2R)

(3:98)

Comparing Equations (3.96) and (3.98) leads to an estimate of the requ ired area S

S ¼ R

(3:99)

S has the same area as the rotor disc but is normal to the ﬂight direction.

Note that the above analysis has been simpliﬁed by assuming that the angle of

attack is small. Actually, the trailing vortices from the rotor are inﬂuenced by their

own induced velocity and so trail downwards behind the rotor. The induced

velocity must therefore have a forward component , which means that the air

100 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

undergoes a rate of change of momentum in the forward direction as well, thus

balancing the drag. The drag is termed induced drag as it comes about by the

backward tilting of the lift force caused by the induced velocity and has nothing to

do with viscosity, it is entirely a pressure drag. Equation (3.92) sho uld also be

modiﬁed to replace V by W, the resultant velocity at the disc, and the area S will be

in a plane normal to W. Also W has a direction which lies close to the plane of the

rotor and so the lift force L will be almost the same as the thrust force F, which is

normal to the plane of the rotor, and by the same argument the induced velocity is

almost normal to the plane of the rotor

u ¼

(2R)

(3:100)

It can be assumed that a wind turbine rotor at high angles of yaw behaves just like

the autogyro rotor.

At zero yaw the thrust force on the wind turbine rotor disc, given by the

momentum theory, is

F ¼ R

r4u(U

 u)(3:101)

where U

now replaces V, so the induced velocity is

u ¼

(2R)

r(U

 u)

(3:102)

The area S now coincides in position with the rotor disc.

Putting W ¼ U

 u to represent the resultant velocity of the ﬂow at the disc in

Equation (3.102) then gives exactly the same Equation as (3.100) which is for a large

angle of yaw. On the basis of this argument Glauert assumed that Equation (3.100),

which is the simple momentum theory, could be applied at all angles of yaw, area

S ¼ R

, through which the mass ﬂow rate is determined, always lying in a plane

normal to the resultant velocity. The rotation of the area S is a crucially different

assumption to that of the theory of Section 3.10.1 (which will now be referred as the

axial momentum theory) and allows for part of the thrust force to be attributable to

an overall lift on the rotor disc.

Thus

F ¼ rR

W2u (3:103)

where

W ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

sin

ª þ (U

cos ª  u)

(3:104)

Thrust is equal to the mass ﬂow rate times the change in velocity in the direction of

the thrust. Both F and u are assumed to be normal to the plane of the disc. The

thrust coefﬁcient is then

THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 101

¼ 4a

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1  a(2 cos ª  a)

(3:105)

The power developed is a scalar quantity and so is the scalar product of the thrust

force and the resultant velocity at the disc W. Hence, the power coefﬁcient is

¼ 4a

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1  a(2 cos ª  a)

(cos ª  a)(3:106)

However, as some of the thrust is attributable to lift on the rotor disc acting as a

circular wing that lift will not extract power from the wind because the net velocity

ﬁeld associated with the lift does not give rise to a ﬂow through the rotor disc. Only

that proportion of the thrust which arises from net ﬂow through the disc will extract

energy from the ﬂow. Consequently, the axial momentum theory is more likely to

estimate the power extraction correctly, whereas the Glau ert theory is more likely

to estimate the thrust correctly.

One very useful concept that emerges from Glauert’s autogyro theory is that he

predicted that the induced velocity through the rotor would not be uniform. The

ﬂow through the yawed rotor is depicted in Figure 3.50 and a simpliﬁcation of the

contributions to the velocity normal to the plane of the rotor along the rotor

diameter parallel to the ﬂight direction are shown. The mean induced velocity

through the rotor, as determined by Equation (3.100), is shown as u

, the normal

component of the forward velocity of the aircraft is U

cos ª, also uniform over the

disc, but, to account for the ﬂow pattern shown, there need s to be a non-uniform

component which decreases the normal induced velocity at the leading edge of the

rotor disc and increases it at the rear. From symmetry, the induced velocity along

the disc diameter normal to the ﬂight direction (normal to the plane of the diagram)

is uniform. The simplest form of the non-uniform component of induced velocity

would be

(r, ł) ¼ u

sin ł (3:107)

cosγ

(r,ψ)

Figure 3.50 Velocities Normal to the Yawed Rotor

102

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

where ł is the blade azimuth angle measu red in the direction of rotation, 08 being

when the blade is normal to the ﬂight direction (or when the wind turbine blade is

vertically upwards), and u

is the amplitude of the non-uniform component which

is dependent on the yaw angle. There would, of course, need to be induced

velocities parallel to the plane of the rotor disc but these are of secondary

importance; the normal induced velocity has a much greate r inﬂuence on the blade

angle of attack than the in-plane component and therefore a much greater inﬂuence

on blade element forces.

The value of u

in Equation (3.107) cannot be determined from momentum theory

but Glauert suggested that it would be of the same order of magnitude as u

. The

total induced velocity, normal to the rotor plane, may then be written as

u ¼ u

1 þ K

sin ł



(3:108)

The value of K must depend upon the yaw angle.

3.10.3 Vortex cylinder model of the yawed actuator disc

The vortex theory for the non-yawed rotor given in Section 3.4 was demonstrated to

be equivalent to the momentum theory in its main results but, in addition, was

shown to give much more detail about the ﬂow-ﬁeld. As the momentum theories of

Sections 3.10.1 and 3.10.2 yield very limited results using the vortex approach for the

yawed rotor may also prove to be useful, giving more ﬂow structure detail than the

momentum theory and, perhaps, a means of allying it with the blade element theory.

The wake of a yawed rotor is skewed to one side because the thru st F on the disc

is normal to the disc plane and so has a component normal to the ﬂow direction.

The force on the ﬂow therefore is in the opposite sense to F causing the ﬂow to

accelerate both upwind and sideways. The centre line of the wake will be at an

angle  to the axis of rotation (axis normal to the disc plane) known as the wake

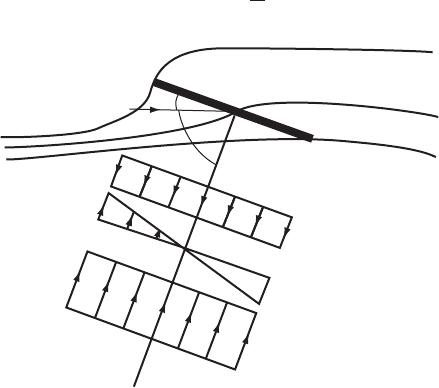
skew angle. The skew angle will be greater than the yaw angle (Figure 3.51). The

Figure 3.51 The Deﬂected Vortex Wake of a Yawed Rotor Showing the Shed Vortices of

Three Blades

THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 103

same basic theory as in Section 3.4 can be carried out for an actuator disc with a

wake skewed to the rotor axis by an angle . There is an important proviso

however: it must be assumed that the bound circulation on the rotor disc is radially

and azimuthally uniform. As will be demonstrated the angle of attack of the blades

is changing cyclically and so it would be impossible for the uniform circulation

condition ever to be valid. What must be assumed is that the variation of circulation

around a mean value has but a small effect on the induced velocity and the wake is

therefore dominated by the vorticity shed from the blade tips by the mean value of

circulation.

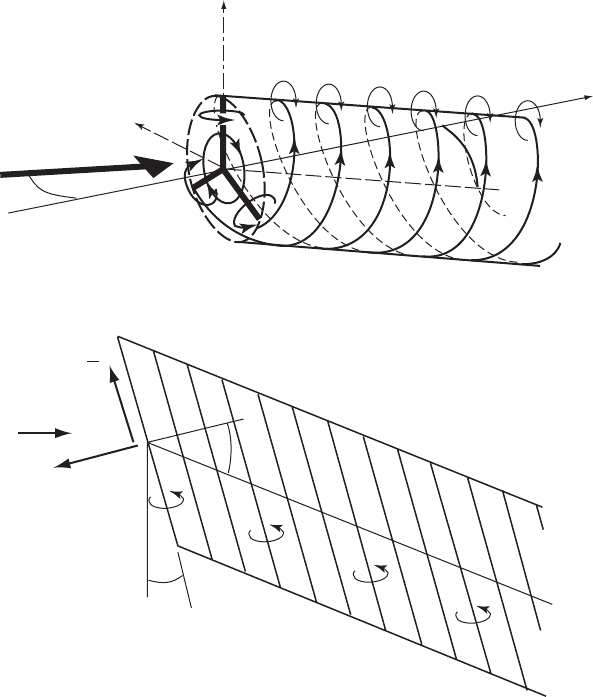
The expansion of the wake again imposes a difﬁculty for analysis and so, as

before, it will be ignored (Figure 3.52).

The analysis of the yawed rotor was ﬁrst carri ed out for purposes of under-

standing a helicopter rotor in forward ﬂight by Coleman et al. (1945) but it can

readily be applied to a wind turbine rotor by reversing the signs of the circulation

and the induced velocities. An inﬁnite number of blades is assumed as in the

∆Γ

Figure 3.52 A Yawed Rotor Wake without Wake Expansion

tan ( )

Figure 3.53 A Yawed Actuator Disc and the Skewed Vortex Cylinder Wake

104

AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES