Burton T. (et. al.) Wind energy Handbook
Подождите немного. Документ загружается.

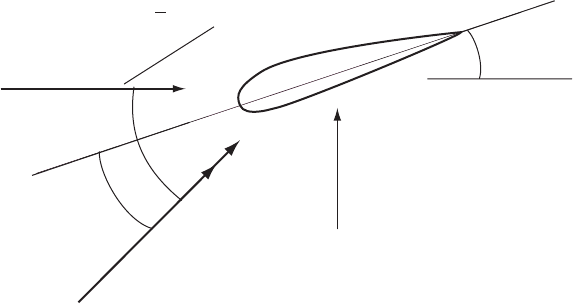
Thus the wake rotatio n produces two velocity components, one in the rotor plane
and one normal to the rotor plane; there is no radial component.
3.10.7 The blade element theory for a turbine rotor in steady yaw
There is doubt about the applicability of the blade element theory in the case of a
yawed turbine because the flow, local to a blade element, is unsteady and because
the theory rep resenting the vortex half of the equation, which replaces the momen-
tum theory, is incomplete in this respect. However, it is not clear how large or
significant are the unsteady forces . If the unsteady forces are large then the blade
element theory is inapplicable and the results of applying the theory will bear no
relation to measured results. If the unsteady forces are small then there should be
some correspondence with actual values. In a steady yawed condition the flow
velocities at a point on the rotor disc do not change with time, if an infinity of blades
is assumed, and so there is no added mass term to consider. However, the change
of angle of attack with time at a point on the blade does mean that the two
dimensional lift force should really be modified by a lift deficiency function similar
to that determined by Theodorsen (1935) for the rectilinear wake of sinusoidally
pitching aerofoil.
Neglecting the effects of shed vorticity the net velocities in the plane of a local
blade element are shown in Figure 3.63. The radial (span-wise) velocity component
is not shown in Figure 3.63 but it is neglected as it is not considered to have any
influence on the angle of attack and therefore on the lift force.
The flow angle is then determined by the components of velocity shown in
Figure 3.63.
Ω •r •(1+a' •cos (χ) •(1 + sin(ψ) •sin (χ)))
+ U
•cos (ψ) •
[
a
•tan
(
χ
)
•(1 + F(r) •K(χ) •sin(ψ)) – sin(γ)
| 2
U
(•cos (γ) – a(1 + F(r)•K(χ) •sin(ψ)))
+ Ω
•r a' •cos(ψ) •sin(χ) (1+sin(ψ) •sin(χ)))
β
φ
α
W
Figure 3.63 The Velocity Components in the Plane of a Blade Cross-Section
THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 115

tan ¼
U
1
(cos ª a(1 þ F( )K()sin ł))
þ ra9cos ł sin (1 þ sin ł sin )
(r(1 þ a9 cos (1 þ sin ł sin )))
þ U
1
cos(ł) a tan
2
(1 þ F( )K()sin ł) sin ª
(3:131)
where r is measured radially from the axis of rotor rotation.
The angle of attack Æ is found from
Æ ¼ (3:132)
Lift and drag coefficients taken from two-dimensional experimental data, just as for
the non-yawed case, are determined from the angle of attack calculation for each
blade element (each combination of and ł).
3.10.8 The blade element–momen tum theory for a rotor in steady
yaw
The forces on a blade element can be determined via Equations (3.131) and (3.132)
for given values of the flow induction factors.
The thrust force will be calculated using Equation (3.46) in Section 3.5.3, which is
for a complete annular ring of radius r and radial thickness r.
L cos þ D sin ¼
1
2
rW
2
Nc(C
l
cos þ C
d
sin )r (3:46)
For an elemental area of the annular ring swept out as the rotor turns through an
angle ł the proportion of the force is
F
b
¼
1
2
rW
2
Nc(C
l
cos þ C
d
sin )r
ł
2
putting C
x
¼ C
l
cos þ C
d
sin and
r
¼
Nc
2r
then
F
b
¼
1
2
rW
2
r
C
x
rrł (3:133)
The values of C
l
and C
d
should really include unsteady effects because of the ever
changing blade circulation with azimuth angle which will depend upon the level of
the reduced frequency of the circulation fluctuation.
If it is chosen to ignore drag, or use only that part of the drag attributable to
pressure, then Equation (3.133) should be modified accordingly.
116 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES
The rate of change of momentum will use either Equation (3.105), Glauert’s
theory, or Equation (3.111), the vortex cylinder theory; in both equations the flow
induction factor a shou ld be replaced by af to account for Prandtl tip loss.
For Glauert’s theory
F
m
¼
1
2
rU
2
1
4af
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 af (2 cos ª af )
p
rłr (3:134a)
Or, for the vortex theory,
F
m
¼
1
2
rU
2
1
4af cos ª þ tan
2
sin ª af sec
2
2
rłr (3:134b)
The Equations (3.134) do not include the drop in pressure caused by wake rotation
but to do this would require greater detail about wake rotation velocities from the
vortex theory. The algebraic complexity of estimating the wake rotation velocities is
great and even then fluctuation of bound circulation is ignored. The drop in
pressure caused by wake rotation, however, is shown to be small in the non-yawed
case and so it is assumed that it can safely be ignored in the yawed case.
The moment of the blade element force about the wake axis is
M
b
¼
1
2
rW
2
Nc(cos ł sin C
x
þ cos C
y
rr
ł
2
where
C
y
¼ C
l
sin C
d
cos
therefore
M
b
¼
1
2
rW
2
r
(cos ł sin C
x
þ cos C
y
)r
2
rł (3:135)
The rate of change of angular momentum is the mass flow rate through an
elemental area of the disc times the tangential velocity times radius.
M
m
¼ rU
1
(cos ª af )rłr 2a9 f r-
2
where
r-
2
¼ r
2
(cos
2
ł þ cos
2
sin
2
ł)
therefore
M
m
¼
1
2
rU
2
1
º4a9 f (cos ª af )(cos
2
ł þ cos
2
sin
2
ł)r
2
rł (3:136)
THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 117
The momentum theory, as developed, applies only to the whole rotor disc where
the flow induction factor a is the average value for the disc. However, it may be
argued that it is better to apply the momentum equations to an annular ring, as in
the non-yawed case, to determine a distribution of the flow induction factors
varying with radius, reflecting radial variation of circulation. Certainly, for the
angular momentum case the tangential flow factor a9 will not vary with azimuth
position because it is generated by the root vortex and although, in fact, the axial
flow factor a does vary with azimuth angle it is consistent to use an annular average
for this factor as well.
To find an average for an annular ring the elemental values of force and moment
must be integrated around the ring.
For the axial momentum case, taking the vortex method as an example,
ð
2
0
1
2
rU
2
1
4af cos ª þ tan
2
sin ª af sec
2
2
rr dł
¼
ð
2
0
1
2
rW
2
r
C
x
rr dł
Therefore
8af cos ª þ tan
2
sin ª af sec
2
2
¼
r
ð
2
0
W
2
U
2
1
C
x
dł (3:137)
The resultant velocity W and the normal force coefficient C
x
are functions of ł. And
for the angular momentum case
ð
2
0
1
2
rU
2
1
º4a9 f (cos ª af )(cos
2
ł þ cos
2
sin
2
ł)r
2
r dł
¼
ð
2
0
1
2
rW
2
r
(cos ł sin C
x
þ cos C
y
)r
2
r dł
which reduces to
4a9 f (cos ª af )º(1 þ cos
2
) ¼
r
ð
2
0
W
2
U
2
1
(cos ł sin C
x
þ cos C
y
)dł (3:138)
The non-dimensionalized resultant velocity relative to a blade element is given by
118 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES

W
2
U
2
1
¼
(cos ª a)
þ ºa9 cos ł sin (1 þ sin ł sin )
2
(3:139)
þ
(º(1 þ a9 cos (1 þ sin ł sin )))
þ cos ł a tan
2
sin ª
2
6
4
3
7
5
2
Note that the flow expansion terms, those terms that involve F( )K(), have been
excluded from the velocity components in Equation (3.139) because flow expansion
is not present in the wake and so there is no associated momentum change. The
blade force, which arises from the flow expansion velocity, is balanced in the wake
by pressure forces acting on the sides of the stream-tubes, which have a stream-
wise component because the stream-tubes are expanding.
Equations (3.137) and (3.138) can be solved by iteration, the integrals being
determined numerically. Initial values are chosen for a and a9, usually zero. For a
given blade geometry, at each blade element position and at each blade azimuth
position ł, the flow angle is calculated from Equation (3.131), which have been
suitably modified to remove the flow expansion velocity, in accordance with Equa-
tion (3.139). Then, knowing the blade pitch angle at the blade element, the local
angle of attack can be found. Lift and drag coefficients are obtained from tabulated
aerofoil data. Once an annular ring (constant ) has been completed the integrals
are calculated. The new value of axial flow factor a is determined from Equation
(3.137) and then the tangential flow factor a9 is found from Equation (3.138).
Iteration proceeds for the same annular ring until a satisfactory convergence is
achieved before moving to the next annular ring (value of ).
Although the theory supports only the determination of azimuthally averaged
values of the axial flow induced velocity, once the averaged tangential flow
induction factors have been calculated the elemental form of the momentum equa-
tion (3.134) and the blade element force (Equation (3.133)) can be employed to yield
values of a which vary with azimuth.
For the determination of blade forces the flow expansion velocities must be
included. The total velocity components, normal and tangential to a blade element,
are then as shown in Figure 3.63 and the result ant velocity is
W
2
U
2
1
¼
(cos ª a(1 þ F( )K()sin ł))
þ ºa9 cos ł sin (1 þ sin ł sin )
2
(3:139a)
þ
(º(1 þ a9 cos (1 þ sin ł sin )))
þ cos ł a tan
2
(1 þ F( )K()sin ł) sin ª
2
6
4
3
7
5
2
THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 119
3.10.9 Calculated values of induced velocity
The measurement of the induced velocities of a wind turbine rotor in yaw has been
undertaken at Del ft University of Technology, (Snel and Schepers, 1995). The tests
were carried out using a smal l wind tunnel model so that a steady yaw could be
maintained in a steady wind with no tower shadow and no wind shear. The rotor
had two blades of 1:2 m diameter which were twisted but had a uniform chord
length of 80 mm. The blade root was at a radius of 180 mm and the blade twist was
98 at the root varying linearly with radius to 48 at 540 mm radius and remaining at
48 from there to the tip. The blade aerofoil profile was NACA 0012. The rotor speed
was kept constant at 720 rev=min and the wind speed was held constant at 6:0m=s.
Tests were carried out at 108,208 and 30 8 of yaw angle.
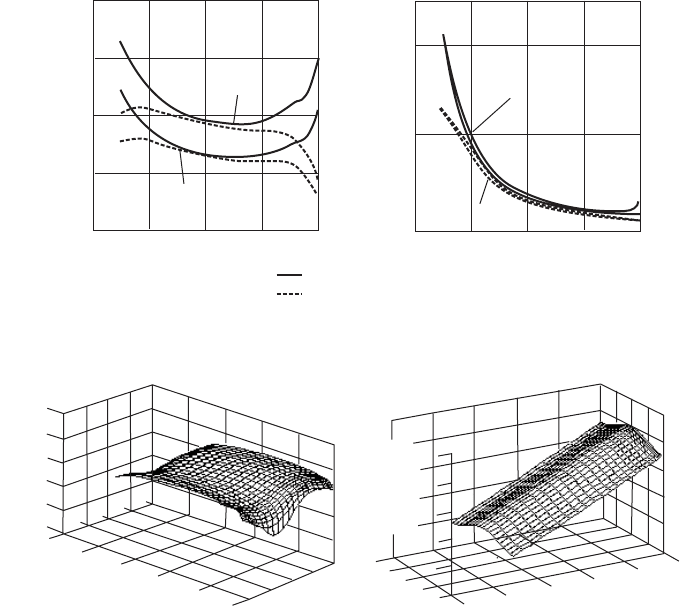
Calculated induced velocities using the vortex momentum equation for the Delft
turbine are shown in Figure 3.64; these are the average values for each annulus
obtained using Eq uation (3.137) and (3.138).
The component velocities at each blade element, as defined in Figure 3.63, are
shown in Figure 3.65. Because of the rotational speed of the blades the tangential
1.0
0.8
0.6
0.4
0.2
0
0
0.2
0.4
0.6
0.8
1
0
0.2
0.4
0.6
0.8
1
10
8
6
4
2
0
360
270
180
90
360
270
180
90
Normal velocity
Tangential
velocity
r/R
r/R
ψ
ψ
Figure 3.65 Component Velocities, Normalized with Wind Speed, at 308 of Yaw
0.4
0.3
0.2
0.1
0
0.2 0.4 0.6 0.8 1
Axial induced velocity
0˚ of Yaw
0˚ of Yaw
30˚ of Yaw
30˚ of Yaw
r/R
r/R
0.02
0.01
0
0.2 0.4 0.6 0.8 1
Tangental induced velocity
Local to the blade
Factored for ti
p
/root loss
Figure 3.64 Azimuthally Averaged Induced Velocity Factors for the Delft Turbine
120
AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES
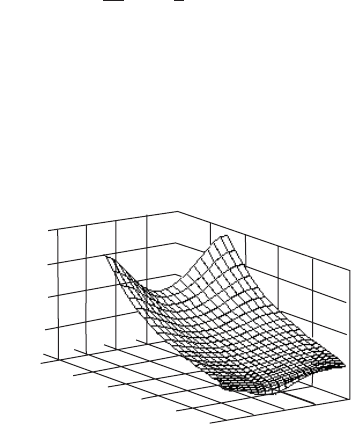
velocity is much greater than the normal velocity but it is the latter which most
influences the variation in angle of attack at the important, outboard sections of the
blades, shown in Figure 3.66.
At the inboard sections of the blades it is the variation in tangential velocity
which mostly influences the angle of attack variation and this is largely as a result
of the changing geometry with azimuth angle rather than the effect of induced
velocity.
3.10.10 Blade forces for a rotor in steady yaw
Once the flow induction factors have been determined blade forces can then be
calculated. Although the flow expansion velocity is excluded from the determina-
tion of the flow induction factors, on the grounds that the consequent blade forces
do not cause any change in the momentum of the flow because flow expansion is
not present in the developed wake, it must be included when the blade forces are
calculated. The flow expansion veloci ty should be dependent on an overall average
value of the axial flow induction factor but it is more convenient to use the annular
average value as determined by Equations (3.137) and (3.138).
The flow angle and the angle of attack need to be determined anew at each blade
element position and at each blade azimuth position Ł because the flow expansion
velocity must now be included, so Equation (3.131) is used in its unmodified form.
Drag must also be included in the determination of forces even if it was not in the
calculation of the induced velocities.
The blade force per unit span normal to the plane of rotation is
d
dr
F
x
¼
1
2
rW
2
cC
x
(3:140)
which will vary with the azimuth position of the blade. The total force normal to
the rotor plane can be obtained by integrating Equation (3.138) along the blade
length for each of the blades, taking account of their azimuthal separation, and
summing the results. The total normal force wil l also vary with rotor azimuth.
Similarly, the tangential blade force per unit span is
20
15
10
5
0
0
0.2
0.4
0.6
0.8
1
r/R
90
180
270
α
ψ
Figure 3.66 Angle of Attack Variation at 308 of Yaw
THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 121

d
dr
F
x
¼
1
2
rW
2
cC
y
and the blade torque contribution about the axis of rotation is
d
dr
Q ¼
1
2
rW
2
crC
y
(3:141)
The total torque is found by integrating along each blade and summing over all the
blades, just as for the norm al force. Again, the torque on the rotor will vary with
azimuth position so to find the average torque will require a further integration
with respect to azimuth.
3.10.11 Yawing and tilting moments in steady yaw
The asymmetry of the flow through a yawed rotor, caused by the flow expansion,
means that a blade sweeping upwind has a higher angle of attack than when it is
sweeping downwind, as shown in Figure 3.61. The blade lift upwind will therefore
be greater than the lift downwind and a similar differential applies to the forces
normal to the ro tor plan e. It can be seen, therefore, that there is a net moment about
the yaw (vertical axis) in a direction which will tend to restore the rotor axis to a
position aligned with the wind direction. The yawing moment is obtained from the
normal force of Equation (3.140)
d
dr
M
z
¼
1
2
rW
2
cr sin łC
x
(3:142)
which will a lso vary with the azimuth position of the blade. The total single-blade
yawing moment at each azimuth position is obtained by integrating Equation
(3.142) along the length of the blade. Summ ing the moments for all blades, suitably
separated in phase, will result in the yawing moment on the rotor.
A similar calcu lation can be made for the tilting moment, the moment about the
horizontal diametral axis (y-axis) of the rotor:
d
dr
M
z
¼
1
2
rW
2
cr cos łC
x
(3:143)
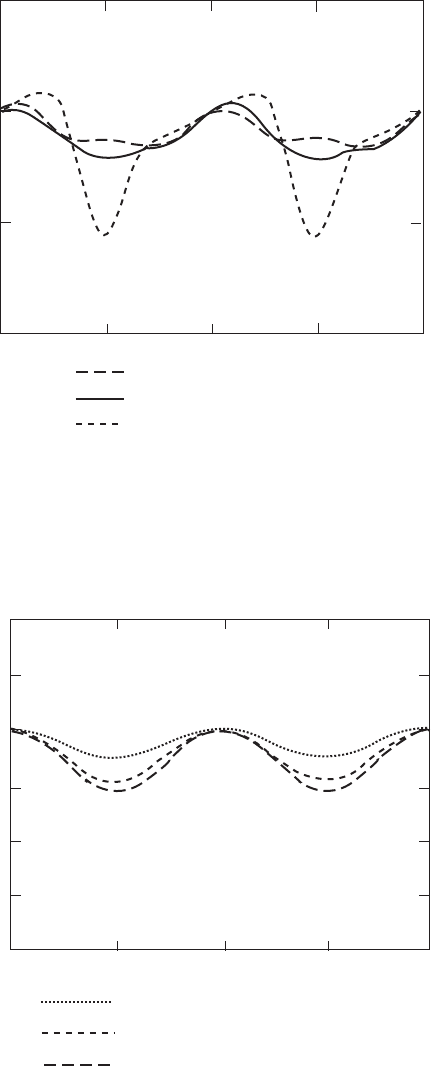
Measured results of rotor yaw moment for the Delft turbine are shown in Figure
3.67 and the corresponding calculated yawing moments are shown in Figure 3.68.
The measured yawing moments were der ived from strai n gauge readings of the
flat-wise bending strain close to the root of the blade at 129 mm radiu s. Flat-wise, or
flap-wise bending causes only displacements normal to the rotor plane. The calcu-
lated yawing moments are determined at the same radial position on the blade and
are, therefore, not the true yawing moments about the actual yaw axis.
The comparison between the measured and calculated yaw moments is quite
good taking into account the limitations of the theory. At 308 of yaw the calculated
values underestimate the measurements significantly whereas at the two lower
122 AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES
yaw = 10˚
yaw = 20˚
yaw = 30˚
0 90 180 270 360
Azimuth angle
M
yaw
(Nm)
1.0
0.0
-1.0
-2.0
Figure 3.67 Measured Yaw Moments on the Delft Turbine, (Snel and Schepers, 1995)
Azimuth angle
Yawing moment in N m
1.0
0.5
0.0
-0.5
-1.0
-1.5
-2.0
0 90 180 270 360
10˚
20˚
30˚
Figure 3.68 Calculated Yaw Moments on the Delft Turbine
THE AERODYNAMICS OF A WIND TURBINE IN STEADY YAW 123
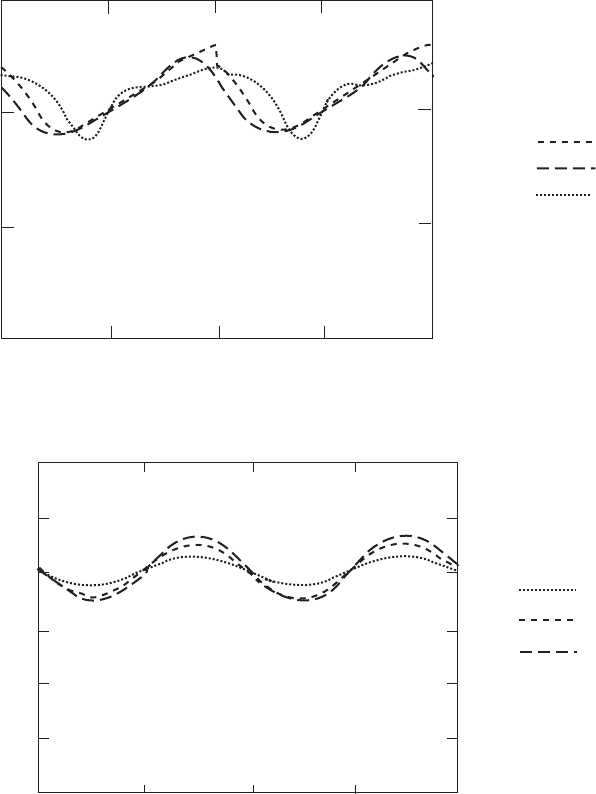
angles the correspondence is much closer. It should be noted that the mean yawing
moment is not zero and that the sign of the moment, being negative, means that it
endeavours to restore the rotor axis to alignment with the wind direction.
The yawing moment comparison is a test of the usefulness of the theory devel-
oped in this section and it would seem that for general engineering purposes it
passes the test.
The measured tilting moments (Figure 3.69) appear to be of about the amplitude
for all three yaw angles whereas the calculated moments (Figure 3.70) increase with
Azimuth angle
M
tilt
(Nm)
0 90 180 270 360
yaw = 10˚
yaw = 20˚
yaw = 30˚
1.0
0.0
-1.0
-2.0
Figure 3.69 Measured Tilt Moments on the Delft Turbine, (Snel and Schepers, 1995)
Azimuth an
g
le
Tilting moment in N m
1.0
0.5
0.0
-0.5
-1.0
-1.5
-2.0
0 90 180 270 360
10˚
20˚
30˚
Figure 3.70 Calculated Tilt Moments on the Delft Turbine
124
AERODYNAMICS OF HORIZONTAL-AXIS WIND TURBINES
