Бураченко Д.Л. Сигнальные конструкции. Часть 3
Подождите немного. Документ загружается.

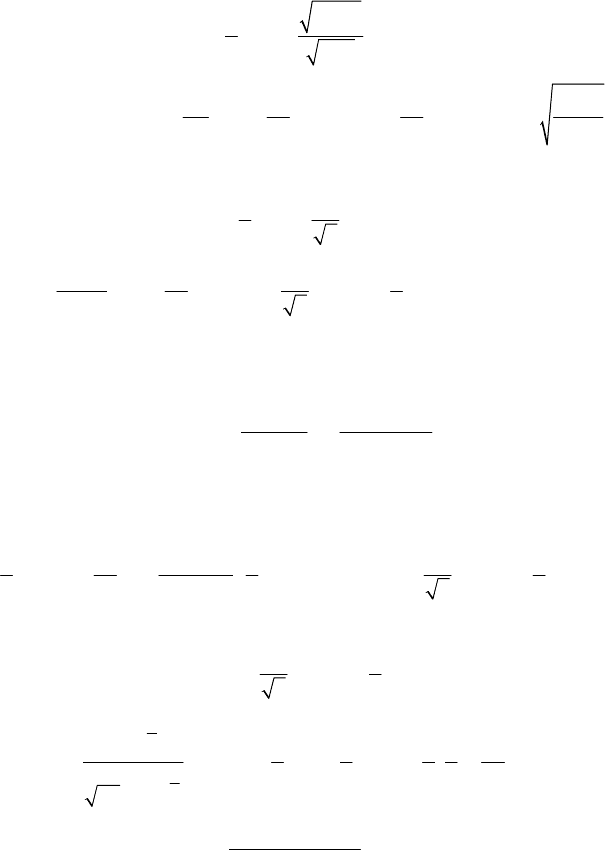
П5.1.1.4. Замирания Райса–Накагами
Для вычисления вероятности ошибки в канале с общими замира-
ниями Райса–Накагами необходимо определить интеграл вида
()
()
2
2
2
0
2
1
,erfc
2
2
bc
bc
gh
Dgh d
m
∞
⎛⎞
⎜⎟
=
μωμ μ
⎜⎟
⎝⎠
∫
,
22
2
2
exp 1, ,
22
p
mMp
⎛⎞⎛
p
⎞
γγ
=− +
⎜⎟⎜
⎜⎟⎜
2
2
2
bc
g
h
m
θ=
где второй момент
⎟
⎟
ββ β
⎝⎠⎝ ⎠
. Пусть ,
тогда
()
()
()
2
0
2
2
1
1
0
1
,erfc
2
2
exp erfc exp .
22
2
2
bc
p
p
p
p
Dgh d
I
d
∞
∞
−
−
θ
⎛⎞
=μωμμ=
⎜⎟
⎝⎠
⎛⎞
βγ θ β
⎛⎞
⎛⎞
=−
μμ
−
μγμμ
⎜⎟
⎜⎟
⎜⎟
⎜⎟
β
⎝⎠
γ⎝⎠
⎝⎠
∫
∫
Приведем несколько вариантов вычисления данного интервала.
I. Воспользуемся разложением функции Бесселя в ряд
()
()
(
)
()
22
1
1
1
0
/4
!
2
k
p
p
p
k
I
kpk
−
∞
−
−
=
γμ
γμ
γμ =
Γ+
∑
.
Тогда
(
)
()
()
2
2
2
21
2
0
0
,
1
exp erfc exp .
22 2 2
2
bc
pk
pk
k
Dgh
d
pk
∞
∞
+−
=
=
⎛⎞
βγ γ θ β
⎛⎞
⎛⎞ ⎛⎞ ⎛ ⎞
=−
μμ
−
μμ
⎜⎟
⎜⎟ ⎜⎟ ⎜ ⎟
⎜⎟
⎜⎟
βΓ+
⎝⎠ ⎝⎠ ⎝ ⎠
⎝⎠
⎝⎠
∑
∫
Используя интеграл [7, с. 104], получаем
()
()
21
2
0
1
2
2
21
1
2
1
erfc exp
2
2
21113
,;;
22 22
2
2
,
pk
kp
kp
pk
pk
d
pk F pk
pk
∞
+−
++
++
+−
+
θβ
⎛⎞
⎛⎞
μμ−μμ=
⎜⎟
⎜⎟
⎝⎠
⎝⎠
⎛⎞
θθ
⎛⎞
=− Γ + + + + − +
⎜⎟
⎜⎟
⎜⎟
β
⎝⎠
⎝⎠
πβ
Γ+
+
β
∫
42
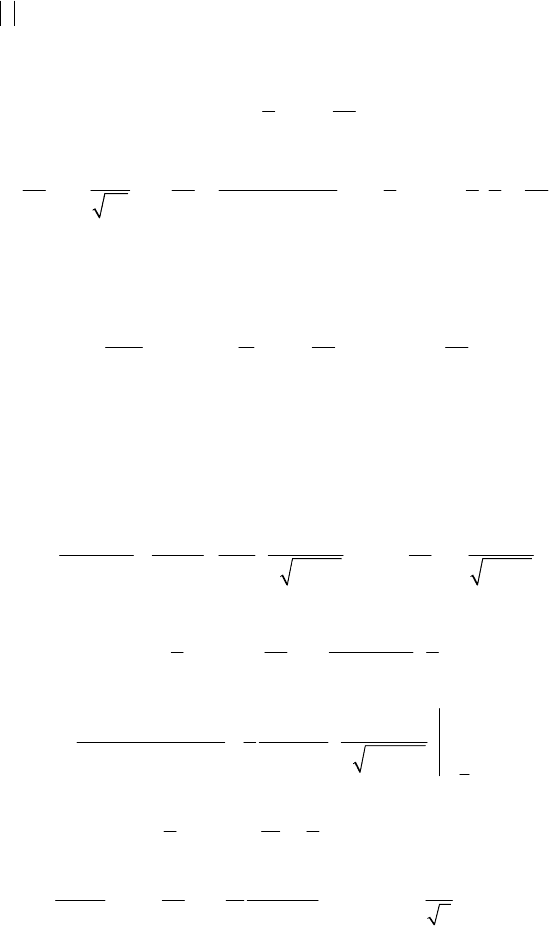
(
21
,;;
)
F
abcz
где
– гипергеометрический ряд Гаусса [3], сходящийся для
всех
1z <
. После несложных преобразований, используя формулу для
суммы бесконечной геометрической прогрессии, получаем при
2
2
γ
<
β
()
()
()
2
2
1
22
21
0
1
,exp
22
0, 5
113
1,
22 222
bc
k
k
Dgh
pk
Fpk
pk
−
∞
=
⎛⎞
γ
=−×
⎜⎟
⎜⎟
β
⎝⎠
⎧⎫
⎛⎞ ⎛⎞ ⎛ ⎞
Γ++
γθγ θ
⎪⎪
×− − ++ −
⎜⎟ ⎜⎟ ⎜ ⎟
⎨⎬
⎜⎟ ⎜⎟ ⎜ ⎟
ββΓ+
πβ
⎪⎪
⎝⎠ ⎝⎠ ⎝ ⎠
⎩⎭
∑
2
;;.
β
Из области сходимости гипергеометрического ряда Гаусса следует, что
эта формула для
(
)
2
,
bc
D
gh
2
θ
<
β
может быть использована при , т. е. при
22
2
exp 1, ,
22
bc
p
hMp
g
⎛⎞⎛
p
⎞
γγ
<− +
⎜⎟⎜
⎜⎟⎜
2
2
2
bc
m
h
g
β
<
или
⎟
⎟
ββ
⎝⎠⎝ ⎠
1
.
II. Предположим, что параметр распределения p – натуральное чис-
ло, т. е. , тогда для нечетных значений
p ∈N
2nm
=
+ интеграл
()
()
2
0
exp erfc
n
n
x
bx cx dx I
∞
−
∫
=
определяется по формуле [7, с. 105]
() ()
21
1
2
1!1
1
2
2
mm
m
m
mm
m
Ic
bb
bb c
+
+
⎛⎞
−−
∂
⎜⎟
=−
⎜⎟
∂
+
⎝⎠
1
2
1
1
2
c
I
b
cb
⎛⎞
⎜⎟
=−
⎜⎟
+
⎝⎠
, .
Следовательно,
()
()
()
()
1
2
2
2
0
1
1
1
2
2
1
,exp
22 2
21!
1
.
2
2
pk
pk
bc
k
pk
pk
pk pk
b
Dgh
pk
pk
b
bb
+−
∞
=
+−
+−
++−
β
=
⎛⎞
−
βγ γ
⎛⎞ ⎛⎞
=
−×
⎜⎟
⎜⎟ ⎜⎟
⎜⎟
βΓ+
⎝⎠ ⎝⎠
⎝⎠
⎛⎞
⎛⎞
⎜⎟
+−
θ∂
⎜⎟
×−
⎜⎟
⎜⎟
β∂
⎜⎟
+θ
⎝⎠
⎜⎟
⎝⎠
∑
22
0
1
exp
2!2
k
k
k
∞
=
ββ
⎛⎞ ⎛⎞
−μ = −μ
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
∑
, то
III. Так как
()
()
()
2
22
1
1
0
0
1
1
, exp erfc .
2!
2
22
k
k
p
pk
bc p
pk
k
Dgh I d
k
∞
∞
+
−
−
=
⎛⎞
−β
βγ θ
⎛⎞
=− μ μγμ
⎜⎟
⎜⎟
⎜⎟
β
γ⎝
⎝⎠
∑
∫
μ
⎠
43
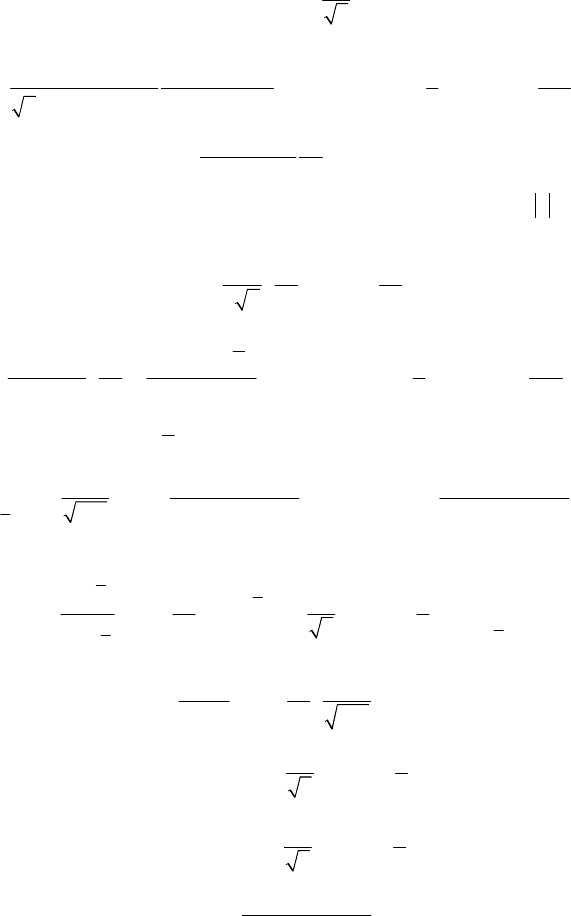
()
2
1
0
erfc .
2
p
pk
p
k
WI
∞
+
−
θ
⎛⎞
d
=μ μ γμ μ
⎜⎟
⎝⎠
∫
Рассмотрим интеграл Воспользо-
вавшись табличным интегралом [7, с. 324], получаем
()
()
()
()
12
22
2
2
0.5
21
,;1,;
2
2
pk
p
k
pk
pk
W Fkpkp kp p
p
pk
−
+
⎛⎞
Γ+ +
γγ
= + ++ ++
⎜⎟
⎜⎟
Γ
θ
π+θ
⎝⎠
,
()
(
)
(
)
()( )
12
22 1 2 1 2
12
0
,;,;
!
k
kk
k
kk
aa
z
Faabbz
bb k
∞
=
=
∑
где
– обобщенная гипергеометри-
ческая функция. Функция
(
)
22 1 2 1 2
,;,;
F
aa bb z z
<
∞
сходится для всех .
Окончательно получаем
()
()
()
()
2
2
2
2
22
22
0
1
,exp
2
2
1
1
1
2
,;1,;
!2
2
p
bc
k
k
k
Dgh
kp
Fpkpk pk p
kpk p
∞
=
⎛⎞
βγ⎛⎞
=−×
⎜⎟
⎜⎟
⎜⎟
β
π
θ
⎝⎠
⎝⎠
⎛⎞
Γ++
⎜⎟
⎛⎞
−
βγ⎛⎞
⎝⎠
× + ++ ++
⎜⎟
⎜⎟
⎜⎟
+Γ
θθ
⎝⎠
⎝⎠
∑
.
3
2
pn
=
+ n
∈
N, . Известно, что [7, с. 730]
IV. Пусть
()
()( )
()()
()
()
()()
1
1
00
2
1! !
1
1
2
!!2 !!2
k
nn
n
zz
kk
n
kk
nk nk
Iz e e
z
knk z knk z
+
−
±±
==
⎡⎤
−+ +
⎢⎥
=±−
⎢⎥
π
−−
⎣⎦
∑∑
.
Учитывая, что , получаем z =γμ
()
()
() ()
() ()
3
3
2
2
2
2
1
1
0
2
2
2
1
12
0
0
1
1
0
, exp erfc exp
22
2
2
1
exp
2
2
2
1erfcexp
2
2
1erfce
2
n
n
bc
n
n
p
p
n
k
knk
n
k
n
knk
n
Dgh I d
Ad
A
+
∞
+
+
+
−
∞
−+
=
∞
+
−+
⎛⎞
βγ θβ
⎛⎞
⎛⎞
=−μμ−μγμ
⎜⎟
⎜⎟
⎜⎟
⎜⎟
β
⎝⎠
⎝⎠
⎝⎠
γ
⎛⎞
βγ
=−×
⎜⎟
⎜⎟
β
πγ
γ
⎝⎠
⎡
θβ
⎛⎞
⎛⎞
×− γμ μ −μ+γμμ+
⎢
⎜⎟
⎜⎟
⎝⎠
⎝⎠
⎢
⎣
θ
⎛⎞
+− γ μ μ
⎜⎟
⎝⎠
∫
∑
∫
∫
μ=
()
()
()()
2
0
xp ,
2
!
.
!!2
n
k
k
n
k
d
nk
A
knk
=
⎤
β
⎛⎞
−μ−γμ μ
⎥
⎜⎟
⎝⎠
⎥
⎦
+
γ=
−γ
∑
44
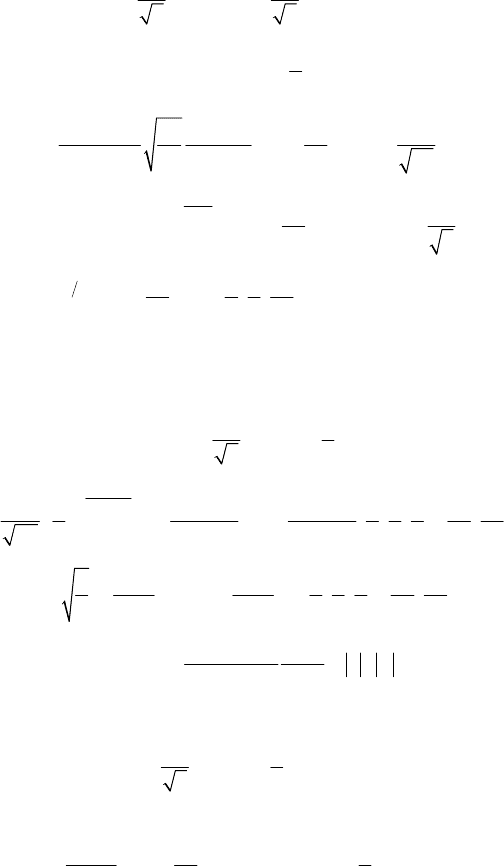
Чтобы воспользоваться табличными интегралами представим интеграл ве-
роятностей в виде
erfc 1 erf
22
θ
⎛⎞ ⎛
θ
⎞
μ
=− μ
⎜⎟ ⎜
⎝⎠ ⎝
⎟
⎠
. В этом случае [7, с. 343, 344]
()
()
()
12
1
0
1
12
1
2
1
2
2
exp
2
1
2
exp erfc
22
2
2exp
4
nk
nk
nk
nk
nk
nk
J
nk D
∞
−+
−+
−+
−+
−
⎛⎞
−+
⎜⎟
⎝⎠
−−+
β
⎛⎞
=μ −μ±γμ=
⎜⎟
⎝⎠
,
⎡
⎤
⎛⎞
⎛⎞
−
π∂ γ γ
==
⎢
⎥
⎜⎟
⎜⎟
⎜⎟
⎜⎟
ββ
β
∂γ
⎢
⎥
⎝⎠
⎝⎠
⎣
⎦
⎛⎞
⎛⎞
γ
γ
=Γ − + β
⎜⎟
⎜⎟
⎜⎟
⎜⎟
β
β
⎝⎠
⎝⎠
∫
m
m
()
22
2
1
2exp ,;
422
2
z
z
Dz
ν
ν
⎛⎞⎛
ν
=−Ψ−
⎜⎟⎜
⎜⎟⎜
⎝⎠⎝
⎞
⎟
⎟
⎠
где
– функция параболического
цилиндра,
(
)
,;abzΨ
– вырожденная гипергеометрическая функция
(функция Трикоми). Второй интеграл преобразуется к виду [7, с. 107]
12
2
0
3
22
2
1
22
1
erf exp
2
2
33131
,;,; ,
222222
2
2133
2 2,;,; , ,
222222
nk
nk
Jd
nk nk
nk nk
∞
−+
−+
−
θβ
⎛⎞
⎛⎞
=μ μ −μ±γμ μ=
⎜⎟
⎜⎟
⎝⎠
⎝⎠
⎡
⎛⎞
θβ −+ −+ θγ
⎛⎞ ⎛ ⎞
=ΓΨ −
⎢
⎜⎟
⎜⎟ ⎜ ⎟
⎜⎟
ββ
π
⎝⎠ ⎝ ⎠
⎢
⎝⎠
⎣
⎤
⎛⎞
−− θγ
⎛⎞
±γ Γ + Ψ + −
⎥
⎜⎟
⎜⎟
⎜⎟
ββ
⎝⎠
⎥
⎝⎠
⎦
∫
2
±
β
()
(
)
(
)
()( )
1
,0
,;, ; , , , 1.
!!
kl
kl k
kl
kl
ab
z
abcc z z
cc kl
∞
+
=
ω
′
Ψω= ω
′
∑
где
<
Следовательно,
искомый интеграл равен
12
12
0
erfc exp
2
2
nk
dJJ
∞
−+
θβ
⎛⎞
⎛⎞
μμ
−
μ
±
γμ μ
=+
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∫
.
V. Рассмотрим интеграл
() () ()
2
2
1
1
0
exp exp
22
2
p
p
p
p
J
QI
∞
−
−
⎛⎞
βγ β
⎛⎞
θ= −
d
μ
θ
μ
−
μγμμ
⎜⎟
⎜⎟
⎜⎟
β
⎝⎠
γ
⎝⎠
∫
45

и применим теорию интегралов, зависящих от параметра, к вычислению
данного определенного интеграла. Действительно, так как
()
22
exp
2
2
Q
⎛⎞
∂θμ
μ
θ
μ
=− −
⎜⎟
⎜⎟
∂θ
π
⎝⎠
,
то
()
()
()
2
122
1
1
0
11
exp exp
22
2
2
p
p
p
p
J
Id
∞
+
−
−
⎛⎞
∂θ
βγ
⎛⎞
=− −
μ
−θ+
βμ γμ μ
⎜⎟
⎜⎟
⎜⎟
∂θ β
π
⎝⎠
γ
⎝⎠
∫
.
2
1
p
p
A
+
−
Полученный интеграл имеет вид
, см. формулу (П5.5), и, следова-
тельно,
() ()
()
()
()
22
11
12
2
2
12
11
exp ; ;
22
2
p
p
Jp
Fp p
p
+
⎛⎞
⎛⎞
∂θ Γ +
βγ γ
⎜⎟
=− − +
⎜⎟
⎜⎟
⎜⎟
∂θ β Γ
π
θ
+
β
⎜⎟
⎝⎠
θ+β
⎝⎠
.
Пусть , тогда
p ∈N
()
()
()
()
22
11
22
0
12
11
;;
2!
22
k
k
k
k
p
Fp p
pk
∞
=
⎛⎞⎛
+
γγ
⎜⎟⎜
+=
⎜⎟⎜
θ+β θ+β
⎜⎟⎜
⎝⎠⎝
∑
⎞
⎟
⎟
⎟
⎠
.
Используя (П5.6) и интегрируя неопределенный интеграл, получаем, что
()
()
()
()
()
()
2
12
22
1
1
2
00
12
11
exp
22
12
1
1
!2 2 1
km
m
pk
m
k
pk
km
k
p
J
p
p
C
pk m
+
+−
∞
+−
==
⎛⎞
Γ+
γ
θ= − − ×
⎜⎟
⎜⎟
βΓ
π
⎝⎠
⎛⎞ ⎛ ⎞
+
−
γθ
×
⎜⎟ ⎜ ⎟
⎜⎟ ⎜ ⎟
β+
θ+β
⎝⎠ ⎝ ⎠
∑∑
.
()
1
0
2
J
=
Константа интегрирования находится из условия
. Так как
, то
(
)
()
p ∈N
()
(
)
1!ppΓ=−
,
()
1
21!
!
2
2
p
pp
π
⎛⎞
Γ+= −
⎜⎟
⎝⎠
()
,
1!
1!
k
pk
p
p
+
−
=
−
и
тогда
(
)
(
)
(
)
1!
k
pppkΓ=+−.
()
2
2
2
2
,
bc
bc
gh
Dgh J
m
⎛⎞
⎜⎟
=
⎜⎟
⎝⎠
Окончательно получаем
.
46
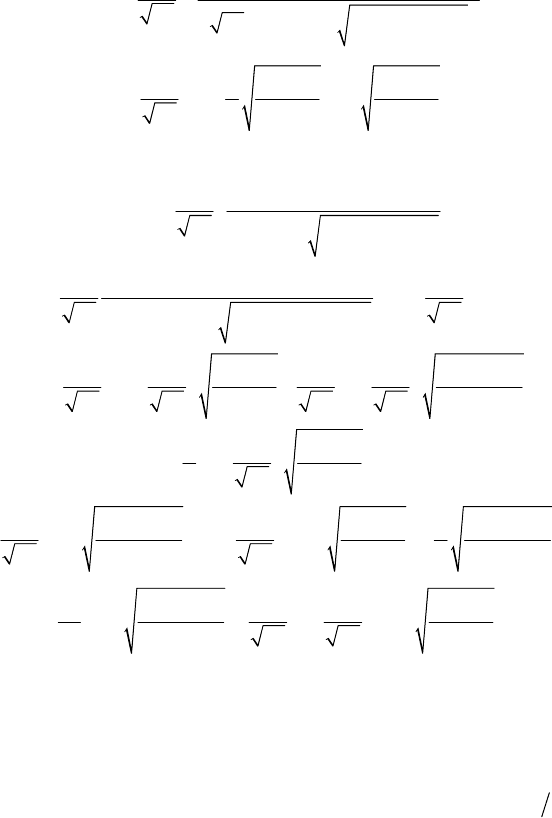
П5.1.2. Точные формулы вероятности ошибки в символе
для двумерных сигналов КАМ-
M при релеевских замираниях
Для средней вероятности ошибки в M-ичном символе для сигналов
КАМ-M при релеевских замираниях справедливо соотношение
()
222
22
22
11
41
21
14
41 1 arctg ,
11
e
bc bc bc
bc bc
bc bc
P
M
Mgh gh gh
gh gh
M
gh gh
⎡
⎢
⎛⎞
⎢
=−
⎜⎟
⎛⎞
⎢
⎝⎠
++ +
⎜⎟
⎢
⎝⎠
⎣
⎤
⎛⎞
⎛⎞
⎥
⎜⎟
+− −
⎜⎟
⎥
⎜⎟
π
⎝⎠ + +
⎝⎠
⎦
1
+
)
где . Для иерархической КАМ
(
0, 5;0, 5; 0gg=
()
()
22 2
2
22 2 22
22
22
2
2
22
22
21
21
11
21 1
1
11
21 21
21 1 1
11
42
1
1
12
arctg 1
1
e
bc bc bc
bc bc bc
bc bc
bc bc
bc
bc
bc
bc
P
M
gh gh gh
MM
gh gh gh
gh gh
MM MM
gh gh
gh
M
gh
gh
M
gh
⎛⎞
=− +
⎜⎟
⎝⎠
++ +
⎛⎞
+−
⎜⎟
⎝⎠
+α +α +α
α
⎛⎞⎛⎞ ⎛⎞
+− − + − −
⎜⎟⎜⎟ ⎜⎟
⎝⎠⎝⎠+ ⎝⎠α+
⎛⎞
−− ×
⎜⎟
π
⎝⎠+
⎡
α
⎢
×+−
⎢
α+
⎣
2
2
−+
22
222
4
arctg
11
bc bc
bc bc
gh gh
M
gh gh
⎤
α
⎛⎞
⎥
2
−
×
⎜⎟
⎥π
⎝⎠ + α+
⎦
22
22
1
arctg
1
bc
bc
gh
M
gh
⎡
α
⎢
×+
⎢
α+
⎣
2
2
12
1arctg
1
bc
bc
gh
MM
gh
⎤
⎛⎞
⎥
−
⎜⎟
⎥
⎝⎠ +
⎦
.
M
П5.2. Системы с двумерными сигналами ФМ-
П5.2.1. Точные формулы вероятности ошибки в бите
В канале с релеевскими замираниями и белым шумом в соответст-
вии с (П5.1) получаем для первых двух бит (
()
(
)
22 2
sin 2 1
jbc
hhK j M=−π
)
47
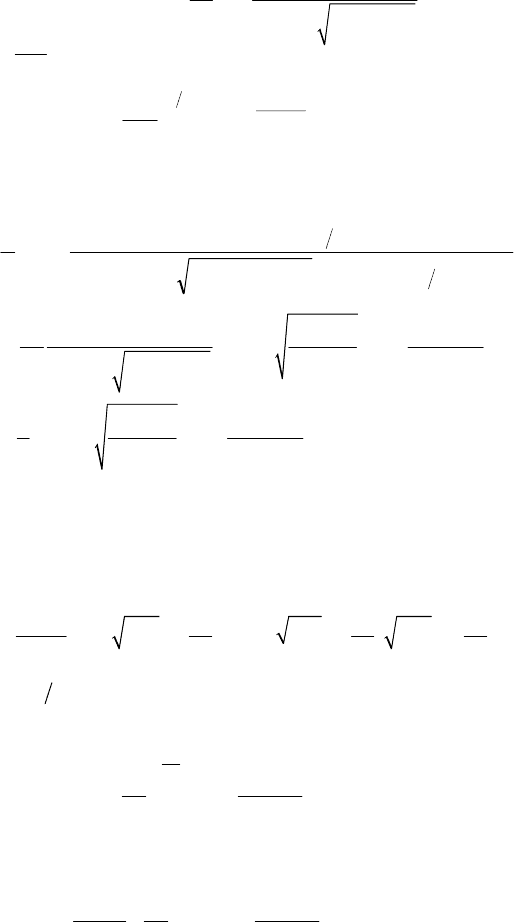
()
/4
12
222
1
21
11
M
bb
j
jjj
PP
M
hhh
=
==
+
++
∑
3,iK=
и для
()
()
1
4
1
1
ent
2
2
1
2
1,
Ki
M
i
j
bi Z bc
j
PT
M
+−
+
⎡⎤
−
⎢⎥
⎣⎦
=
=−
∑
,hMj
,
Где
(
)
()()
()
()()
[]
+
ψ+π−
⎥
⎦
⎤
⎢
⎣
⎡
+++
π−
π
=
=
j
bcbcbc
bc
Z
MjKhKhKh
Mj
jMhT
12sin112
12cos
arcsin
1
,,
222
2
()
()
2
2
222
21
11
arcsin cos
2
1
11
bc
bc
jjj
j
hK
M
hK
hhh
⎡
⎤
−
π
⎛⎞
⎢
⎥
+⋅
⎜⎟
π⎢
+
⎝⎠
++ +
⎥
⎣
⎦
,
()
2
2
21
1
arccos cos
2
1
bc
j
bc
j
hK
M
hK
⎡⎤
−
π⎛⎞
⎢⎥
ψ= ⋅
⎜⎟
⎢⎥
+
⎝⎠
⎣⎦
.
где
П5.2.2. Точные формулы вероятности ошибки в M-ичном символе
2
M
≥
Известно [1], что вероятность ошибки в M-ичном символе ( )
двумерного сигнала ФМ-M при когерентном приеме в канале с детерми-
нированными параметрами и белым шумом равна
222
2
2sin 2 2sin ,2cos
2
em m
M
PQh Vh h
M
MM
−π π
⎛⎞⎛
=+ −
⎜⎟⎜
⎝⎠⎝
M
π
⎞
⎟
⎠
, (П5.7)
2
0mm
hEN= , – максимальная энергия сигналов ФМ-M, N
m
E
где
0
– од-
носторонняя спектральная плотность мощности белого шума, а
()
22
00
1
,exp
22
x
xy
Vd
xdy
β
α
α
⎛⎞
+
αβ = −
⎜⎟
⎜⎟
π
⎝⎠
∫∫
0
β
≥
, , , 0
α
≥
– функция Никольсона. С другой стороны, известно определение функции
Оуэна в виде двукратного интеграла [5]:
()
22
00
arctg 1
,exp
22 2
vax
axy
Tva dxdy
⎛⎞
+
=− −
⎜⎟
⎜⎟
ππ
⎝⎠
∫∫
, , . 0a ≥0
ν
≥
48
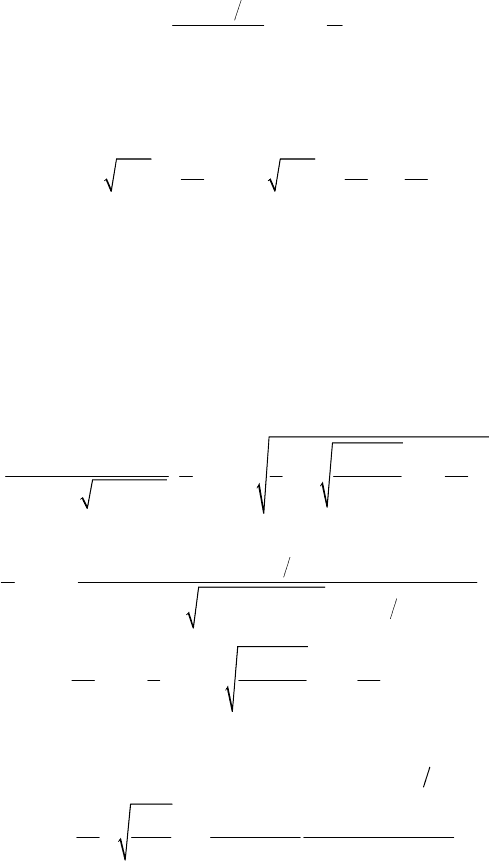
Из сопоставления следует, что функции Никольсона и Оуэна связа-
ны соотношением
()
(
)
arctg
,
2
V
βα
,T
β
⎛
αβ = − α
⎜
⎞
⎟
π
α
⎝⎠
. (П5.8)
В результате, подставляя (П5.8) в (П5.7), получим представление
вероятности ошибки в M-ичном символе двумерного сигнала ФМ-M
через функцию Оуэна:
e
P
22
2sin 2 2sin,ctg
em m
PQ h T h
M
MM
π
ππ
⎛⎞⎛
=+
⎜⎟⎜
⎝⎠⎝
⎞
⎟
⎠
.
Преимущество этого представления по сравнению с классическим
представлением через функцию Никольсона состоит в том, что вычисле-
ние вероятности ошибки сводится к вычислению однократных табули-
рованных интегралов: функции Лапласа
e
P
(
)
Qx
(
)
,Tva
и функции Оуэна .
П5.2.2.1. Релеевские замирания
Средняя вероятность ошибки в M-ичном символе при релеевских
замираниях для сигналов ФМ равна
() ()
2
2
121
arcsin 1 cos
2
11
1
bc
e
bc
hK
P
M
hK
⎤
⎛⎞
⎛⎞
⎡
π
⎛⎞
⎥
⎜⎟
⎜⎟
⎢
=⋅+
⎜⎟
+
⎥
⎜⎟
⎜⎟
π
⎢
⎝⎠
Ω+ + Ω Ω+
+
⎜⎟
⎥
⎣
⎝⎠
⎝⎠
⎦
()
()
()
()
222
cos
2
arcsin
21 1sin2
bc bc bc
M
hK hKhK M
⎛⎞
⎜⎟
π
⎜⎟
+
π
⎛⎞
⎜⎟
+
++π
⎜⎟
⎜⎟
⎝⎠
⎝⎠
,
+ψ
22
sin
bc
hK
M
π
Ω=
2
2
1
arccos cos
2
1
bc
bc
hK
M
hK
⎡
⎤
π
⎛⎞
⎢
⎥
ψ= ⋅
⎜⎟
⎢
⎥
⎝⎠
+
⎣
⎦
,
.
где
П5.2.2.2. Замирания Накагами
()
2
2
log sin
g
MM=π
В этом случае при и
1, mm≥∈N
2
1
1
bc
e
g
h
P
M
=− −
π
()
()
1
1
0,5
2
0
1
1!
mk
m
mk
k
bc
m
mk
gh m
−−
−
−−
=
×
−−
+
∑
49
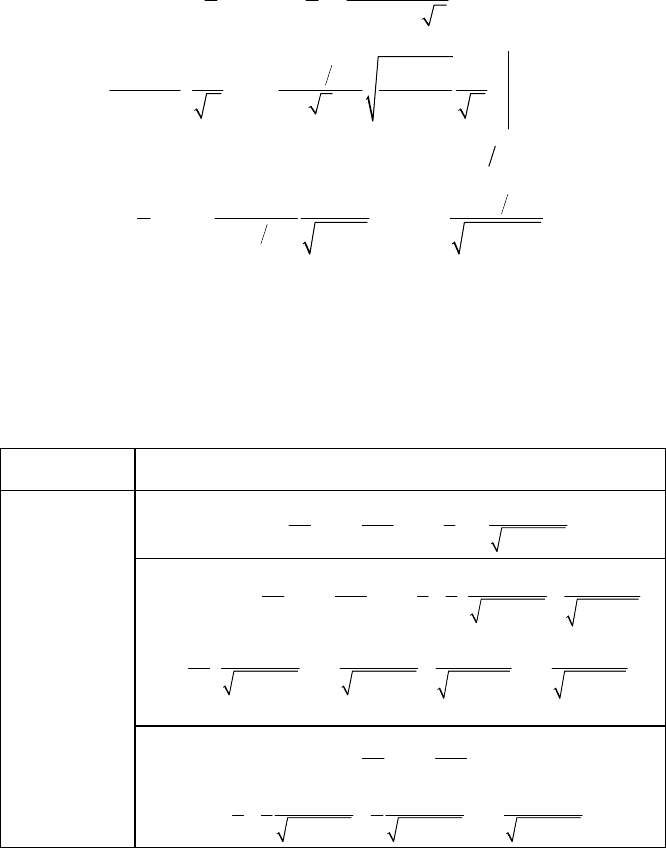
()
()
1
0,5
2
1
12
0,5
1
11
22
2
ctg
11
arctg
2
mk
mk
mk
bc
mk
bc
p
mk
M
gh
pp
pghm
−−
−−
−−
−−
=
⎡
−
⎛⎞
⎢
×Γ −− + ×
⎜⎟
⎢
⎝⎠
π
⎣
⎤
⎡⎤
⎛⎞
π
⎥
∂
⎢⎥
⎜⎟
×
⎥
⎢⎥
⎜⎟
∂+
⎥
⎝⎠
⎣⎦
⎦
.
12m
=
)
Для односторонне-нормальных замираний (
()
()
22
ctg
111
arctg arctg .
sin
212
e
bc bc
M
P
M
Kh Kh
⎡⎤
⎛⎞⎛
π
⎢⎥
⎜⎟⎜
=+
⎢⎥
⎜⎟⎜
ππ
+
⎢⎥
⎝⎠⎝
⎣⎦
⎞
⎟
⎟
⎠
П5.3. Интегралы
В табл. 5.1 приведены интегралы, которые могут быть использова-
ны при расчете вероятности ошибки в канале с замираниями для сигналь-
ных конструкций, рассмотренных в прил. 4.
Таблица П 5.1
Плотность
ИНТЕГРАЛ
распределения
()
22
22
0
1
exp 1
2
2
1
Qd
∞
⎛⎞
μμ ασ
⎛⎞
⎜⎟
αμ − μ = −
⎜⎟
⎜⎟
σσ
⎝⎠
+
ασ
⎝⎠
∫
()()
22
22 22
0
22 22 22 22
11
exp
44
2
11
1
arctg arctg
2
1111
QQ d
∞
⎛⎞
μμ ασ βσ
⎛⎞
⎜⎟
α
μβμ − μ=− + +
⎜⎟
⎜⎟
σσ
⎝⎠
+α σ +β σ
⎝⎠
⎛⎞
ασ βσ βσ ασ
⎜⎟
++
⎜⎟
π
+ασ+ασ+βσ+βσ
⎝⎠
∫
Релея
()
2
22
0
22 22 22
exp
2
11 1
arctg
42
11 1
Qd
∞
μμ
⎛⎞
αμ − μ =
⎜⎟
σσ
⎝⎠
ασ ασ ασ
=− +
π
+
ασ +ασ +ασ
∫
50
Продолжение табл. П5.1
Плотность
ИНТЕГРАЛ
распределения
()()()
22
0
22 22 22
22 22 22 22
22 22 22 22
22
exp
2
11
88
111
1
arctg arctg
4
1111
1
arctg arctg
4
1111
1
arc
4
1
QQQ d
∞
μμ
⎛⎞
αμ βμ γμ − μ =
⎜⎟
σσ
⎝⎠
⎛⎞
ασ βσ γσ
⎜⎟
=− + + +
⎜⎟
+α σ +β σ +γ σ
⎝⎠
⎛⎞
ασ βσ βσ ασ
⎜⎟
+
++
⎜⎟
π
+ασ+ασ+βσ+βσ
⎝⎠
⎛⎞
βσ γσ γσ βσ
⎜⎟
+
++
⎜⎟
π
+βσ+βσ+γσ+γσ
⎝⎠
ασ
+
π
+α σ
∫
,
22 22 22
22
22 22 22 22
2
22 22
tg arctg
11 1
1
arctg arctg
4
1111
arctg
11
⎛⎞
γσ γσ ασ
⎜⎟
+
−
⎜⎟
+α σ +γ σ +γ σ
⎝⎠
⎛
ασ βγσ βσ αγσ
⎜
−
++
⎜
π
+α σ Δ +α σ +β σ Δ +β σ
⎝
⎞
γσ αβσ
⎟
+
⎟
+γ σ Δ +γ σ
⎠
()
22 2 2
1
Δ
=+σα+β+γ
Релея
()
3
22
0
22 22
22
22 22 22
exp
2
13 3
88 2
11
1
arctg arctg
2
111
Qd
∞
μμ
⎛⎞
αμ − μ =
⎜⎟
σσ
⎝⎠
ασ ασ
=− + ×
π
+α σ +α σ
⎛⎞
ασ α σ
⎜⎟
×−
⎜⎟
3
+
ασ +ασ + ασ
⎝⎠
∫
()
22
0
22 22
,exp
2
arctg 1
arctg
22
11
Td
∞
μμ
⎛⎞
αμ β − μ =
⎜⎟
σσ
⎝⎠
βασ αβσ
=−
ππ
+α σ +α σ
∫
51
