Бураченко Д.Л. Сигнальные конструкции. Часть 3
Подождите немного. Документ загружается.

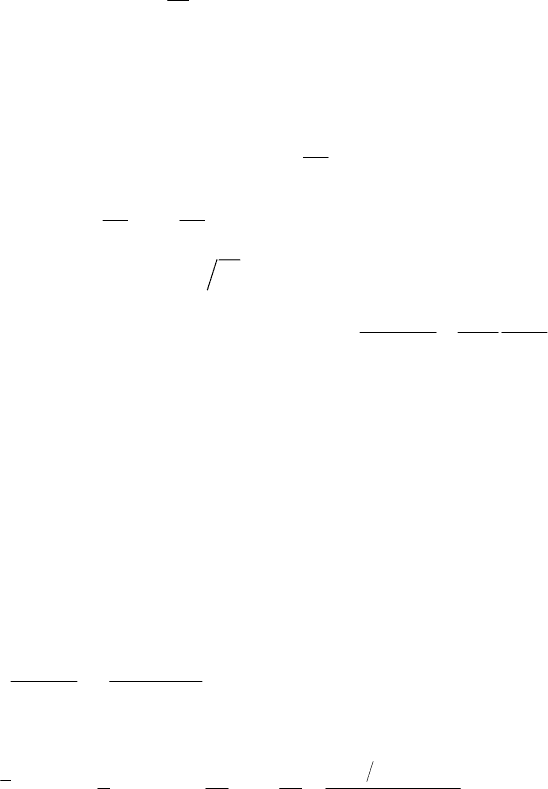
Частными случаями распределения Накагами являются односто-
роннее нормальное (
1m
=
) и релеевское (
0,5m
=
). Двухпараметрическое
распределение Накагами (m,
2
μ
) принципиально не может воспроизвести
структуру четырехпараметрического распределения.
Распределение Райса–Накагами при соответствующем выборе пара-
метров обобщает распределения Релея, Райса и Накагами (m-
распределение). Так, при
,,p γβ
2
1
β=
σ
1p
=
, ,
0γ=
получаем распределение
Релея; при ,
0
2
μ
γ=
σ
2
1
β=
σ
1p =
, – распределение Райса, а при значениях
параметров , ,
2
2m
β
=μ
0γ=
pm= получаем распределение Накагами.
При выборе значения следует учесть, что
(
)
()
1
11
0
11
lim
2
p
pp
I
p
−
−−
γ→
γμ
=
Γ
γ
0γ=
,
где
()
x
Γ
– гамма-функция [3].
Распределение Райса–Накагами важно еще и потому, что оно вхо-
дит в распределение Бекмана, которое состоит из линейных комбинаций
распределения Райса–Накагами при целом положительном значении p. В
таком случае определение вероятности ошибки для этого закона распре-
деления фактически приводит к решению задачи для трехпараметрическо-
го закона распределения случайного коэффициента передачи канала μ.
Определим начальные моменты для плотности распределения Рай-
са–Накагами. Воспользовавшись разложением функции Бесселя в ряд
()
()
(
)
()
22
1
1
1
0
/4
!
2
k
p
p
p
k
I
kpk
−
∞
−
−
=
γμ
γμ
γμ =
Γ
+
∑
и определением гамма-функции, не-
сложно получить следующее выражение:
()
()
()
/2
22
0
2
2
exp
22 !
k
n
nn
k
npk
m
kpk
∞
=
⎛⎞⎡⎤
Γ
++
⎡⎤
γγ
μ= = −
⎜⎟
⎢⎥
⎢⎥
⎜⎟
βββΓ+
⎣⎦
⎢⎥
⎝⎠⎣⎦
∑
.
(
)
(
)
1
x
xxΓ+=Γ
Применяя формулу
и определение вырожденной гипер-
геометрической функции Куммера
(
)
(
)
11
,, ;;
M
abx F abx=
[3], получим
формулу для начальных моментов
32
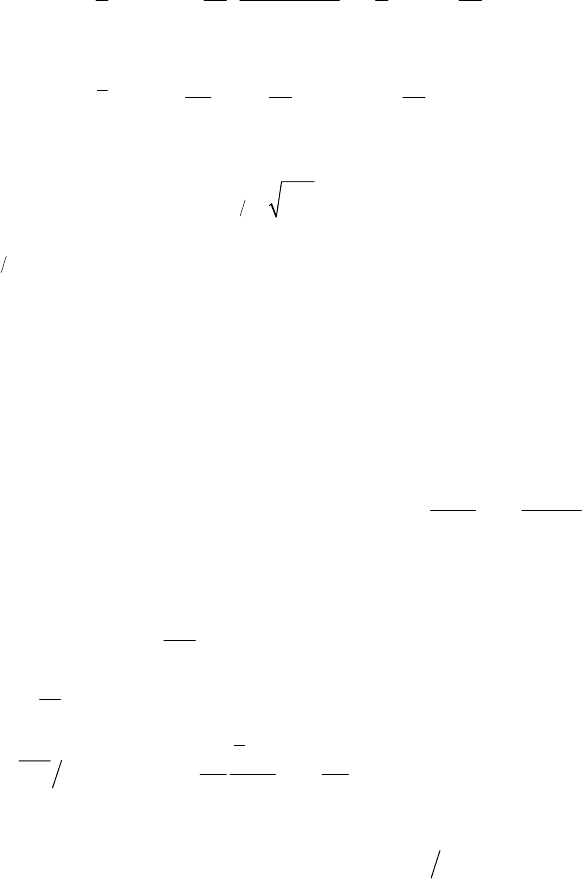
()
()
/2
22
0,5
2
exp , ,
22
n
n
np
n
mM
p
⎛⎞ ⎛
Γ+
⎡⎤
2
pp
⎞
γ
γ
=− +
⎜⎟ ⎜
⎢⎥
⎜⎟ ⎜
⎟
⎟
β
βΓ β
⎣⎦
⎝⎠ ⎝
⎠
.
В частности, второй момент, необходимый для вычисления ошибки, равен
22
22
2
exp 1, ,
22
p
mMp
⎛⎞⎛
p
⎞
γγ
μ= = − +
⎜⎟⎜
⎜⎟⎜
⎟
⎟
ββ β
⎝⎠⎝ ⎠
.
Вероятность ошибки при общих замираниях определяется как
()
2
c,μ
0
eb
PP h d
∞
⎛⎞
=
ω
μμ
⎜⎟
⎝⎠
∫
, (П5.1)
eb
P
где
– вероятность ошибки (в символе/бите) в канале с детерминиро-
ванными параметрами и белым шумом, μ – коэффициент передачи. Ос-
новная сложность заключается в вычислении интеграла вида (П5.1) от
функции Лапласа, их произведения, а также от функции Оуэна и получе-
нии аналитических формул, удобных для проведения расчетов. Функции
Лапласа и Оуэна входят во все формулы вероятности ошибок в симво-
ле/бите двумерных сигналов [5, прил. 4].
Дадим краткую характеристику методики расчета вероятности ошиб-
ки при медленных общих замираниях. Пусть
c,μ c,пер
22
c,μ
00
PT P T
h
NN
==μ
,
, где
2
c,μ c,пер
PP=μ
c,
P
μ
– мощность принятого сигнала, а – мощ-
ность переданного сигнала. Тогда математическое ожидание мощности сиг-
нала определяется как
c,пер
P
() ()
2
c, c, c,пер 2c,пер
00
PP dP dmP
∞∞
μμ
=ωμμ= μωμμ=
∫∫
,
где
2
2
m =μ
– начальный момент второго порядка. Следовательно,
c,пер c, 2
PP
μ
= m
c,μ
22 2
c,μ c
20 2
1
PT
h
mN m
=μ =μ
2
1
h
и . При расчете по (П5.1)
необходимо вместо величины , в формуле для вероятности ошибки в
гауссовском канале, подставить величину
2
h
222
c,μ c2
hh=μ m
и вычислить
полученный интеграл.
33
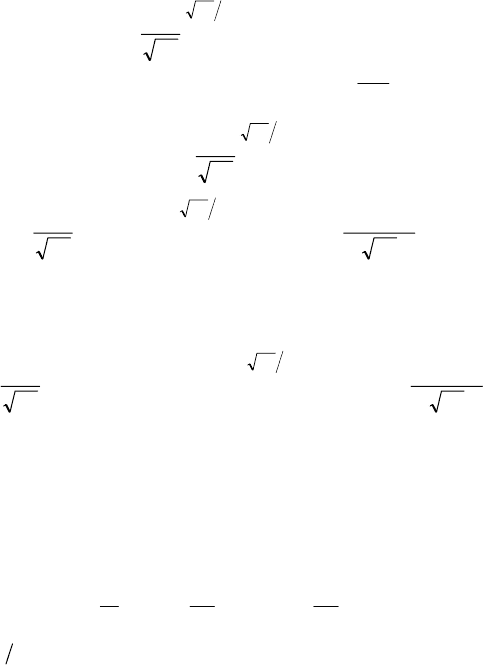
В приложении представлены формулы вероятности ошибки для ,
и в системах с квадратурной амплитудной манипуляцией (КАМ),
иерархической КАМ и фазовой модуляции (ФМ).
e
P
bi
P
b
P
П5.1. Системы с квадратурной амплитудной модуляцией
П5.1.1. Точные формулы вероятности ошибки в бите
для двумерных сигналов КАМ-M/2
При применении разновидности манипуляционного кода Грея, реа-
лизуемого, в частности, в стандарте цифрового телевидения DVB-T [4],
средние вероятности ошибки в первом и втором бите
()
()
∑
=
==
2
1
2
12
,1;5,0;
2
M
j
bcbb
hjgD
M
PP
. (П5.2а)
3,kK=
Средняя вероятность ошибки в k-м бите (
2
log
K
M
=
, ):
()()
()
()
()
()
()
()
()
[]
() ()
()
()
×
⎪
⎩
⎪
⎨
⎧
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−ν−−δ+
+
⎪
⎭
⎪
⎬
⎫
νν+νν−×
×
⎪
⎩
⎪
⎨
⎧
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−−+
+==
∑∑
∑∑
∑
−
−
−
−
−
=
−
−
+=ν
−ν
−
==ν
−ν
=
−
1
1
2
1
2
2
1
1
12
12
1
221
2
1
2
1
1
2
1
12,2,
12
ent2121
2
,2;,0;22
12
ent211
2
0;5,0;
2
k
k
k
k
k
k
M
j
k
k
bcbc
k
M
j
k
M
j
k
kbkb
M
j
M
k
hjgDhjgD
M
j
M
jgD
M
PP
()
(
.,2,,
2
⎪
⎭
⎪
⎬
⎫
ν×
bc
hjgD
)
(П5.2б)
Средняя вероятность ошибки на бит в K-битовом блоке, определен-
ная как
11
,2 1 ,2
11
11 1
11 1
,
KK
K
bbi bi
ii i
PP P P
KK K
−
== =
== =
∑∑ ∑
bi
1
2
K
K= , может быть представлена в виде
где
34
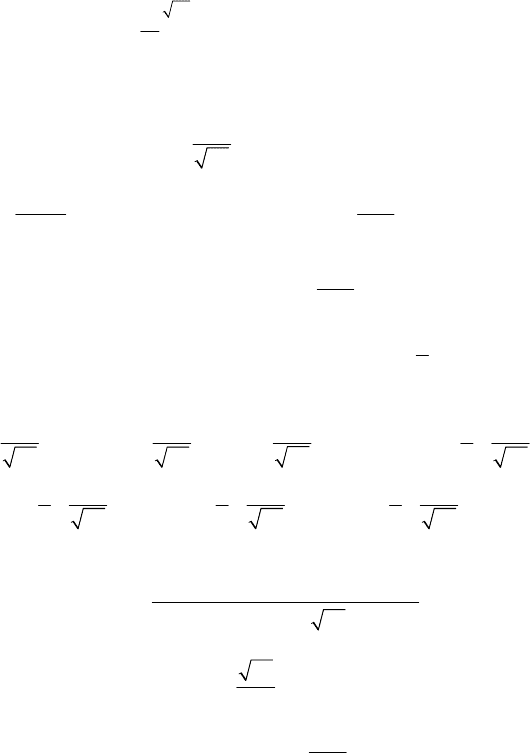
(
1
2
21 1
1
1
,
M
bj
j
PaDg
K
−
−
=
=
∑
)
bc
h
, (П5.2в)
21
j
a
−
где коэффициенты определены, например, в [5],
21 21 21
1
4
jj j
a
M
−
⎛⎞
=α − β
⎜⎟
⎝⎠
1
1
−
, = , ,
1
1
β
=
α
−
()
,
1
21 ,
1
0
11
1 1 2 1 2ent 2 1
2
2
j
j
qj
j
U
Uq
jq
Uq
q
j
−
ν−
−
+
=
⎡
⎤
⎡⎤
−
⎛⎞
⎢
α= +− ⋅ − −ν+
j
⎥
⎢⎥
⎜⎟
⎢
⎝⎠
⎣⎦
⎦
⎣
∑
,
()
,
1
21 , ,
0
1
11 12ent 21
2
j
qj
U
jqj
q
q
j
ν−
−
=
qj
⎡
⎤
−
⎛⎞
β=+− ν − −ν+
⎢
⎥
⎜⎟
⎝⎠
⎣
⎦
∑
,
() ()
1
2,
1
ent log 1 , ent 1 2
2
q
jqj
Uj j
+
⎡
⎤
=−ν=−
⎡⎤
⎣⎦
+
⎢
⎥
⎣
⎦
.
В частности,
1
1
41a
M
⎛⎞
=−
⎜⎟
⎝⎠
3
2
41a
M
⎛⎞
=−
⎜⎟
⎝⎠
5
4
a
M
=−
9
13
4
2
a
M
⎛⎞
=−
⎜⎟
⎝⎠
7
0a
=
, , , , ,
11
14
4
2
a
M
⎛⎞
=−
⎜⎟
⎝⎠
13
13
4
2
a
M
⎛⎞
=− −
⎜⎟
⎝⎠
15
14
4
2
a
M
⎛⎞
=− −
⎜⎟
⎝⎠
, , .
В (П5.2) используются следующие соотношения:
()
()
()()
2
1
3
(, , )
2131 1
21 21 ( 1),
2
0; 2,
1
() ent .
1; 3,
2
K
ggj
MM
M
j
k
k
k
k
β−
=
νχ = ×
⎡
⎤
−+ α− +α−
⎣
⎦
⎡⎤
×−+ν− +χα−
⎢⎥
⎣⎦
=
⎧
+
⎡⎤
δ= β=
⎨
⎢⎥
≥
⎣⎦
⎩
(П5.3)
Формулы (П5.2) справедливы для любой модели замираний, вклю-
чая рассмотренные во введении. Ниже, для конкретных замираний, будут
определены
(
)
2
,
bc
D
gh
. Параметр α определяет кратность увеличения ми-
нимального евклидового расстояния d только между точками созвездия,
ближайшими к координатным осям (вариант, используемый в стандарте
DVB-T) по сравнению с минимальным евклидовым расстоянием между
35

остальными точками созвездия. В частном случае при 1
α
= получаем
классическую КАМ, при
– иерархическую КАМ.
2, 4
α
=
П5.1.1.1. Райсовские и релеевские замирания
В этом случае
()
22 2
2
22 22
222
22
0
22 22 22
,,,
2
11
21
11
exp ,
222
11
bc bc
bc
bc bc
bc bc
bc bc bc
gh gh
Dg h Ρ
gh gh
gh gh
I
gh gh gh
⎡⎤
γ
π
⎢⎥
=−
⎢⎥
++γ ++γ
⎣⎦
2
1
⎡
⎤⎡ ⎤
++γ
γγ
−⋅−
(П5.4)
+γ
⎢
⎥⎢ ⎥
++γ ++γ ++γ
⎢
⎥⎢ ⎥
⎣
⎦⎣ ⎦
где P-функция и ее свойства определены в работе [6],
()
()
2
22
0
1
,, exp
11 sin
z
Pz q d
q
ϕ
⎡
⎤
⎢
⎥
ϕ
=− α
⎢
⎥
π
−− α
⎢
⎥
⎣
⎦
∫
,
где – вещественные числа,
,zq 0/2
≤
ϕ≤π . Из приведенных ниже
свойств видно, что она включает в себя, как частные случаи, функции Ла-
пласа, Оуэна и Маркума.
Отметим несколько основных свойств P-функции:
()
,,0 2
2
Pz Q z
π
⎛⎞
=
⎜⎟
⎝⎠
() ()
,,0 2 1 2
4
Pz Q z Q z
π
⎛⎞
⎡
⎤
=−
⎜⎟
⎣
⎦
⎝⎠
, ,
()
,arctg ,0 2 ,
2
h
PaT
⎛⎞
=
⎜⎟
⎝⎠
ha
;
() ()
() ()
()()
22
0
22
0
1
,, , exp
22 2 2
1
,exp
22
1
1, ,, 0;
2
yx yx x y
PQxyIxy
yx
xy
Qyx I xy
Qxy Qyx y x
⎛⎞
⎛⎞
−π− +
⎜⎟
⎜⎟
=
−−
⎜⎟
⎜⎟
=
+
⎝⎠
⎝⎠
⎛⎞
+
⎜⎟
=+ − =
⎜⎟
⎝⎠
=+ − ≥≥⎡⎤
⎣⎦
() ()
[]
()
()
;0,0,
2
exp
2
1
sgn,
2
,
2
sgn1
2
1
,
22
0
≥≥
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−+
+−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
π
−
+−−=
yx
yx
xyI
xy
xy
xyxy
PxyyxQ
36
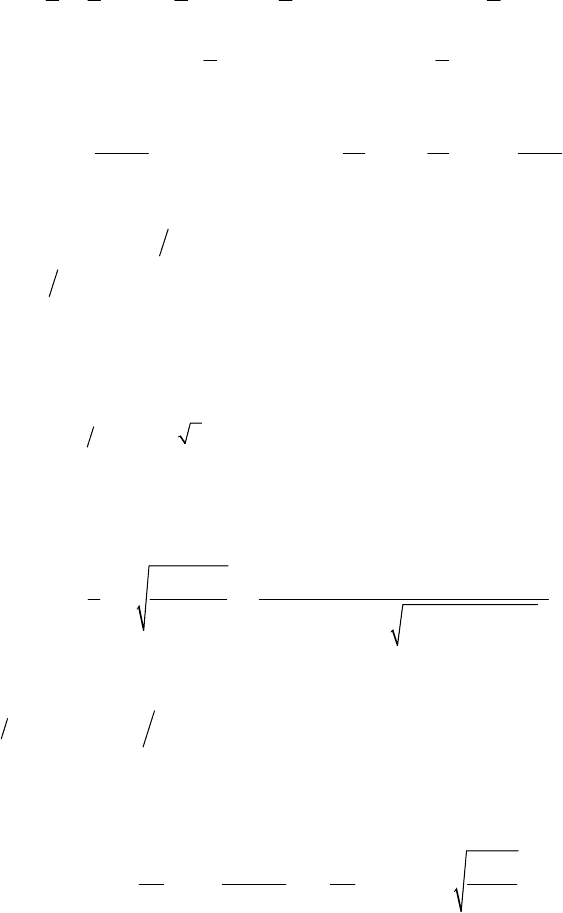
1
,, , , , , , 0, 0,
22
z
PPzqPzqq
qq
⎛⎞
2
π
ππ
⎛⎞⎛ ⎞ ⎡
ϕ= − −ϕ >ϕ∈
⎜⎟
⎜⎟⎜ ⎟
⎤
⎢
⎥
⎝⎠⎝ ⎠ ⎣
⎝⎠
⎦
;
() ()
,, 2 , , , , , ,
22
Pz q Pz q Pz q
ππ
⎛⎞ ⎡⎤
ϕ
=−π−
ϕϕ
∈π
⎜⎟
⎢
⎥
⎝⎠ ⎣
⎦
.
Здесь
()
()
2
2
2
0
1
,exp1
22
1
a
hd
Tha x
() ()
22
0
,exp
2
y
tx
Qxy t I txdt
∞
⎛⎞
+
=−
⎜⎟
⎜⎟
⎝⎠
∫
x
x
⎡⎤
=−+
⎢⎥
π
+
⎢⎥
⎣⎦
∫
и –
соответственно функция Маркума и функция Оуэна.
222
0
2
γ
=μ σ
Параметр
– отношение мощности регулярной состав-
ляющей
2
0
2μ
2
σ
к дисперсии рассеянной (флуктуирующей) составляю-
щей коэффициента передачи μ канала с райсовскими замираниями. В ча-
стных случаях при
2
0
γ
= получаем канал с релеевскими замираниями,
при
2
γ
→∞ – канал без замираний. В этом случае, используя свойство P-
функции
()
(
)
,2,0 2Pz Q zπ= нетрудно получить известные формулы
для канала без замираний.
2
0
γ
=
В канале с белым шумом и релеевскими замираниями (
) по-
лучаем
()
() ()
2
2
2
222
11
,1
2
1
21
bc
bc
bc
bc bc bc
gh
Dg h
gh
gh gh gh
⎡⎤
⎢⎥
=− =
⎢⎥
.
1
⎡
⎤
+
++ +
⎣⎦
⎢
⎥
⎣
⎦
(
)
2
0
0,
bc
Nh→→∞
В канале без помех
с учетом свойства
()
(
)
2
,2,1 exp 2Pz zπ=−
(
)
2
2
lim , 0
bc
bc
h
Dgh
→∞
=
получаем .
(
)
2
,
bc
D
gh
Получим еще одно представление для
в виде ряда. Рас-
смотрим интеграл
() ( )
22
0
222
0
exp
2
aa
J
QId
∞
⎛⎞
μμ+⎛⎞
θ= θ
2
2
2
bc
g
h
m
μ
−
μμ
⎜⎟
⎜⎟
⎜⎟
σσσ
⎝⎠
⎝⎠
∫
,
θ=
,
37
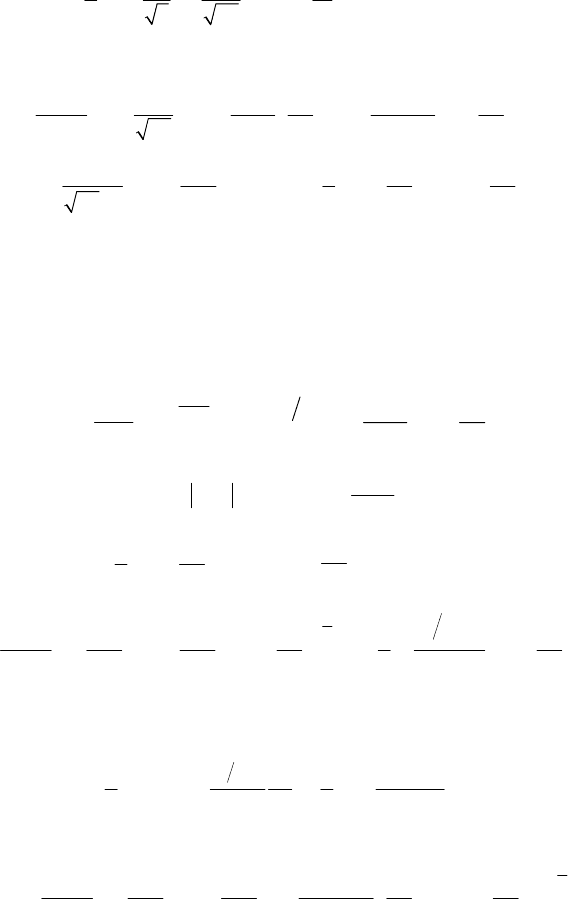
()
2
11
erfc exp
22
22
x
x
Qx dt
∞
⎛⎞
⎛⎞
==−
⎜⎟
⎜⎟
⎜⎟
π
⎝⎠
⎝⎠
∫
t
где – интеграл Лапласа. Диффе-
ренцируя интеграл
(
)
J
θ
по параметру θ, получаем
()
22 2 2
0
222
0
2
222
0
22 2 2
0
exp exp
2
2
2
111
exp exp .
2
22
J
aa
Id
aa
I
d
∞
∞
⎛⎞⎛ ⎞
∂θ
μθμμμ+⎛⎞
=− − −
μμ
=
⎜⎟⎜ ⎟
⎜⎟
⎜⎟⎜ ⎟
∂θ
π
σσσ
⎝⎠
⎝⎠⎝ ⎠
⎛⎞
⎛⎞
⎛⎞⎛⎞
=− −
μ
−θ+
μμμ
⎜⎟
⎜⎟
⎜⎟⎜⎟
⎜⎟
πσ σ σ σ
⎝⎠⎝⎠
⎝⎠
⎝⎠
∫
∫
В дальнейшем будет очень полезна формула для вычисления интеграла,
содержащего экспоненту и модифицированную функцию Бесселя порядка
ν [7, с. 306]
()
()
()
12
0
2
2
11
1
exp
2
1
;1;
24
1
2
Ax pxIcxdx
c
cp F
p
∞
αα−
νν
α+ν
−
ν
ν+
=− =
⎛⎞
α+ν⎡⎤
α+ν
=Γ ν+
⎜⎟
⎢⎥
⎜⎟
ν+
⎣⎦
⎝⎠
∫
(П5.5)
,
[
]
Re , Re 0, argpcα+ν > <π
()
()
a
a
b
b
Γ
⎡⎤
Γ=
⎢⎥
Γ
⎣⎦
где
;
. Применяя эту формулу,
при ,
2
a
c =
σ
2
2
11
2
p
⎛
⎞
⎟
3α=
=θ+
⎜
σ
⎝⎠
0, = , получаем
ν
()
()
2
3
2
1
2
2
22
11
222 2
113
exp ;1;
22
22
a
J
a
F
1
−
−
⎛⎞
σ
⎛⎞
⎜⎟
∂θ
⎛⎞ ⎛⎞
=− − θ + θ +
⎜⎟
⎜⎟
⎜⎟ ⎜⎟
⎜⎟
∂θ
σσσ σ
⎝⎠ ⎝⎠
⎜⎟
⎝⎠
⎝⎠
.
Воспользуемся разложением гипергеометрического ряда (функции Кум-
мера):
(
)
()
11
0
32
3
;1;
21
(
)
!
k
k
k
k
z
Fz
k
∞
=
⎛⎞
=
⎜⎟
⎝⎠
∑
,
2
21
3
2
2!
k
k
k
k
+
⎛⎞
=
⎜⎟
⎝⎠
!
(
)
1!
k
k,
=
.
Таким образом,
() ()
()
3
2
2
2
2
22 32 2
3
0
21!
11
exp
22
2!
kk
k
k
Jk
aa
k
−
−
∞
=
⎛⎞
∂θ +
⎛⎞⎛ ⎞
=− − θ +
⎜⎟
⎜⎟⎜ ⎟
⎜⎟
∂θ
σσ σ σ
⎝⎠⎝ ⎠
⎝⎠
∑
.
38
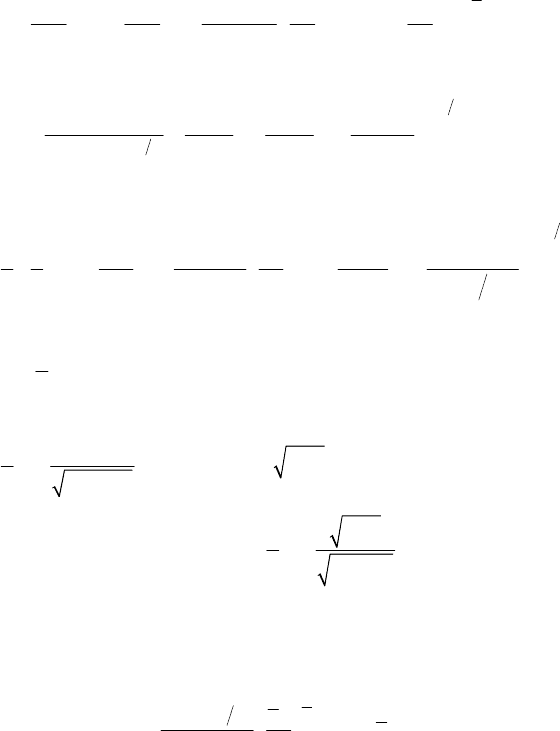
Отсюда согласно определению неопределенного интеграла вытекает, что
(
)
(
)
()
()
3
2
2
2
2
22 32 2
3
0
21!
11
exp
22
2!
kk
k
k
JJd
k
aa
d
k
−−
∞
=
′
θ= θ θ=
⎛⎞
+
⎛⎞⎛ ⎞
=− − θ + θ
⎜⎟
⎜⎟⎜ ⎟
⎜⎟
σσ σ σ
⎝⎠⎝ ⎠
⎝⎠
∫
∑
∫
,
или, используя табличный интеграл
()
() ()
12
2
12 2 2 2
22
0
11
21
k
nk
n
k
n
nn
k
dx x
C
k
axa
xa
+
+
=
⎛⎞
±−
=
⎜⎟
⎜⎟
+
±
⎝⎠
±
∑
∫
, (П5.6)
можно записать, что
()
()
()
()
()
12
22 2
232
22
3
00
21! 1
11
exp
22 2 1
2
1
2!
m
k
m
k
m
k
k
km
k
aa
JC
m
k
+
∞
==
⎛⎞
⎛⎞ ⎛⎞
+−
θ
⎜⎟
θ= − −
⎜⎟ ⎜⎟
⎜⎟
⎜⎟ ⎜⎟
+
σσ
θ+ σ
⎜⎟
⎝⎠ ⎝⎠
⎝⎠
∑∑
.
Здесь учтено, что константу интегрирования можно найти из усло-
вия
()
1
0
2
J =
.
0a
=
(распределение Релея) получаем
В частности, при
()
22
1
1
2
1
J
⎛⎞
θσ
⎜⎟
θ= −
⎜⎟
+
θσ
⎝⎠
2
bc
g
hθσ =. Так как , получаем
()
()
2
2
2
1
,1
2
1
bc
bc
bc
gh
Dgh J
gh
⎛⎞
⎜⎟
=θ= −
⎜⎟
+
⎝⎠
.
П5.1.1.2. Замирания Накагами
Для распределения Накагами начальные моменты определяются по
формуле
()
()
2
2
2
n
n
mn
m
mm
Γ+
μ
⎛⎞
=
⎜⎟
Γ
⎝⎠
22
m
=
μ, .
(
)
2
,
bc
D
gh
При вычислении
будем использовать интеграл [7, с. 104]
39
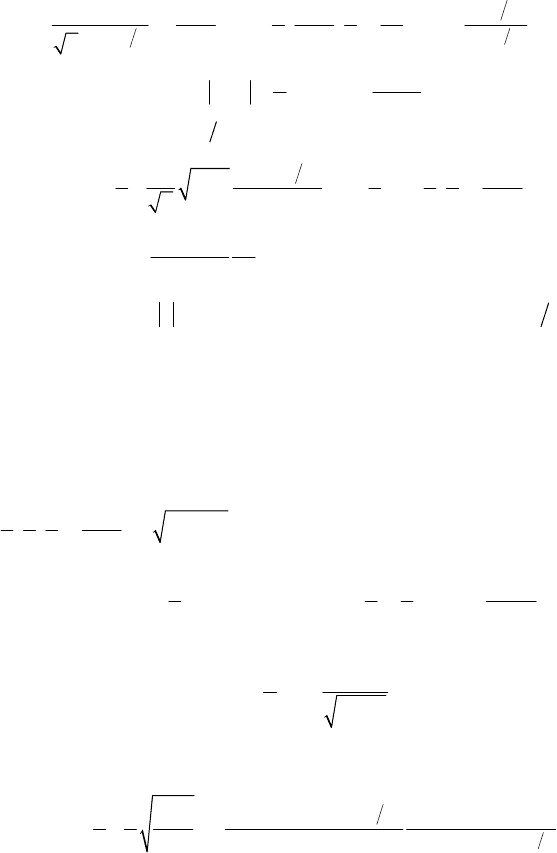
()
()
()
()
()
12
0
2
21
2
12
erf
exp
erfc
20
1113
,;;
1
2 222
2
cx
xpx dx
cx
cc
F
p
p
p
∞
α−
α
α+
⎧⎫
⎪⎪
−=
⎨⎬
⎪⎪
⎩⎭
⎛⎞
Γα
⎧⎫
α+ α+
⎛⎞
=± Γ − +
⎜⎟
⎨⎬
⎜⎟
⎜⎟
⎝⎠
⎩⎭
π
⎝⎠
∫
,
(
)
11
Re 0, arg , Re
42
pc
±
π
><α>−
.
12m ≥
Тогда для любых
()
()
()
2
22
21
12
11 1 13
,,
22
bc
bc bc
m
gh
Dgh gh F m
mm
⎛⎞
Γ+
=− + −
⎜⎟
⎜⎟
Γ
π
⎝⎠
;;,
22
()
(
)
(
)
()
21
0
,;;
!
k
kk
k
k
ab
z
F abcz
ck
∞
=
=
∑
где – гипергеометрический ряд (ряд Гаус-
са), сходящийся при
(
)
(
)
(
)
(
)
(
)
11
k
aaa ak aka=+ +−=Γ+ΓK
1z
<
; ,
, – символ Похгаммера [7]. Из условия сходимости
ряда Гаусса следует, что эта формула может использоваться при
()
0
1a =
1, 2, 3k = K
2
bc
g
hm
<
.
Если (распределение Релея), то, используя свойство гипер-
геометрической функции
1m =
()()
21
,;; 1
a
F
abbz z
−
=−
, получаем
2
2
21
133
,;; 1
222
bc
bc
gh
F
gh
m
⎛⎞
−=+
⎜⎟
⎜⎟
⎝⎠
. Аналогично для односторонне-нормального
замирания, т. е. при
2
21
1 3 arctg
,1; ;
22
z
Fz
z
⎛⎞
−=
⎜⎟
⎝⎠
1
2
m
=
, учитывая, что , полу-
чаем
(
)
2
2
11
,arctg
2
bc
bc
Dgh
g
h
=
π
.
При m ∈
N, используя метод интегрирования по частям, находим,
что
()
()
()
()
1
2
1
2
12
2
0
12
11 1
,
22 1!
mk
m
bc
bc
mk
k
bc
mmk
gh
Dgh
mk
gh m
−−
−
−−
=
Γ−−
=−
π−−
+
∑
,
или после простейших преобразований имеем
40
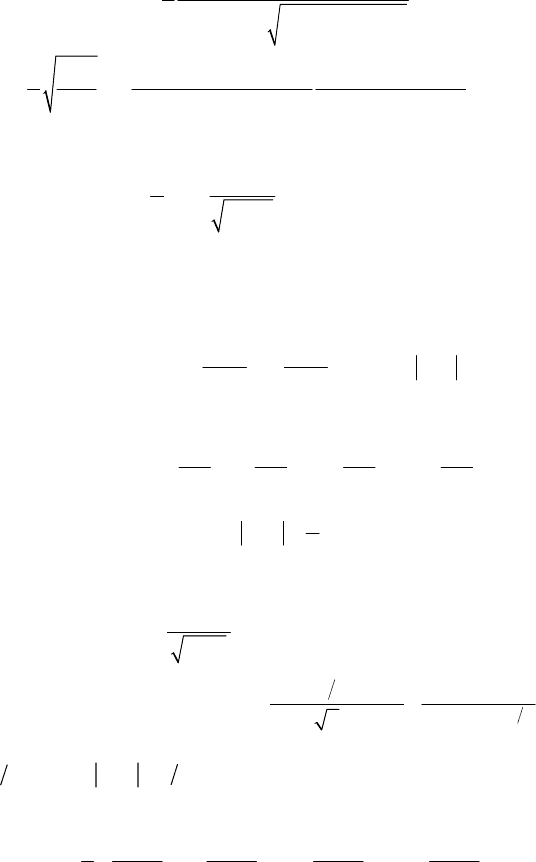
(
)
()
()
()
()
2
222
1
2
2
0,5
2
0
1
,
2
0,5
11
.
21!
bc
bc bc bc
mk
m
bc
mk
k
bc
m
Dgh
gh m gh gh m
mmk
gh
mk
gh m
−−
−
−−
=
=−
++ +
Γ−−
−
π−−
+
∑
Для односторонне-нормальных замираний аналогично предыдущему слу-
чаю получаем
(
)
2
2
11
,arctg
2
bc
bc
Dgh
g
h
=
π
.
П5.1.1.3. Левинские замирания
В этом случае необходимо использовать следующие интегралы [7,
с. 343]
()
12
0
2
22
xKcxdx c
∞
α− α− −α
ν
α
+ν α−ν
⎛⎞⎛
⎞
⎟
⎠
=ΓΓ
⎜⎟⎜
⎝⎠⎝
∫
,
Re Re ; Re 0c
α
>ν >
и [7, с. 415]
() ()
22 2
01
22 2 2
0
1
erf exp
88 8 8
cc c
xbxKcxdx K K
bb b b
∞
0
⎡
⎤
⎛⎞⎛⎞ ⎛⎞
=−
⎢
⎥
⎜⎟⎜⎟ ⎜⎟
⎜⎟⎜⎟ ⎜⎟
⎢
⎥
⎝⎠⎝⎠ ⎝⎠
⎣
⎦
∫
,
Re 0, arg
4
cb
π
><,
() ()
01
,
K
xKx
– функции Макдональда [3],
где
() ( )
()
0
2
00
cos
cos sh
1
x
t
K
xxtdt dt
t
∞∞
==
+
∫∫
() ( ) ( )
0
exp ch chxxttdt
∞
ν
=− ν
∫
.
K
и
()
()() ()
()
12
22
0
12 2 coszxt
K
xz dt
x
tz
ν
∞
ν
νν
Γν+
=
π
+
∫
Другое определение
+
,
arg 2z
<
π
, , 0x > . Re 1 2ν≥−
Для канала с левинскими замираниями
()
2
10
22 2 2
11 1 1 1
,exp
2
42 2 2
bc
bc bc bc bc
Dgh K K
gh gh gh gh
⎡⎤
⎛⎞⎛⎞⎛⎞
⎢⎥
=− −
⎜⎟⎜⎟⎜⎟
⎜⎟⎜⎟⎜⎟
⎢⎥
⎝⎠⎝⎠⎝⎠
⎣⎦
,
41
