Бураченко Д.Л. Сигнальные конструкции. Часть 3
Подождите немного. Документ загружается.

2
c
0
2
2
mm
md
QQ Q gh
N
⎛⎞
⎛⎞
==
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
0, 2;
()
1, 3;
κ
=
⎧
δκ =
⎨
κ
≥
⎩
1
2,
K
κ=
где , ,
1
3K ≥
b
,
()()
()
2
1
3
2131 1
K
g
MM
α
=
⎡⎤
−+α− +α−
⎣⎦
() ()(
1
21 212 1.
2
M
mj
κ−
2
1m
g
mg=
)
=
ν− + − + α−
,
,
3, 4i
=
2
κ
=
В частности, при
( ) получаем
(
)
4
34 21
1
4
[(21)2( 1)(21) /2] [(21)2( 1)(21) ]
1
4
2
.
M
bb j
j
M
jMjM
j
PP Q
M
QQ
M
−
=
−+α−+ν− −+α−+ν−
=
== +
+−
∑
∑
При ( ) имеем
5, 6i =
3κ=
[]
[
{
/8
,6 ,5
21
1
/8
(2 1) / 4] [(2 1) 2( 1) / 4 ]
1
[(21) /2] [(21)2( 1) /2]
[ (2 1) 2( 1) 3 / 4 ] [ (2 1) 2( 1) ]
[(2 1) 2( 1) 5 /4] [(2 1) 2(
8
2
2
2
2
M
bb
j
j
M
jM j M
jM j M
jMjM
jMj
PP Q
M
QQ
M
QQ
QQ
QQ
−
=
−+ −+ α−+
ν=
−+ −+ α−+
−+ α−+ −+ α−+
−+ α−+ −+ α−
== +
⎡
⎤
++
−
⎢
⎥
⎣
⎦
⎡⎤
−+
⎣⎦
⎡⎤
−−
⎣⎦
+−
∑
∑
−
+
}
1) 3 / 4 ]
.
M+
⎡⎤
⎣⎦
Для последней пары бит
()
()
() ()
()
()
()
4
1
,1 , 1
1
41 41
4121 4121
21
1
(4 1) 2( 1) (4 1) 2( 1)
41
2
12
2
2
1
2
M
bK bK
M
M
M
PPQ
M
QQ Q Q
M
QQ
M
ν−
−
ν=
ν− ν+
ν− + α− ν+ + α−
−
ν−
ν− + α− ν+ + α−
ν= +
⎧
⎛⎞
⎪
==+ − −ν×
⎜⎟
⎨
⎜⎟
⎪
⎝⎠
⎩
×−+ν − +
⎛⎞
+−−ν −
⎜⎟
⎜⎟
⎝⎠
∑
∑
.
При из (П4.4) следуют как частные случаи формулы для ,
полученные для двумерной классической КАМ. Полная (средняя по всем
) вероятность ошибки на бит в K-битовом блоке будет
bi
P1α=
bi
P
12
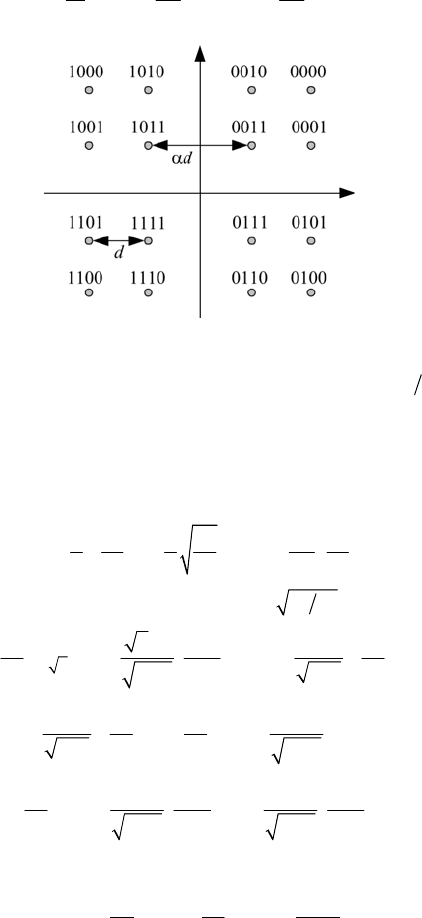
11
,2 1 ,2
11
11 1
11 1
KK
K
bbi bi
ii i
PP P P
KK K
−
== =
== =
∑∑ ∑
bi
.
Рис. П4.1
П4.1.4. Системы с двумерными сигналами КАМ- 2M ,
упакованными в «крест»
Отличие этой системы от классических сигналов КАМ состоит в
том, что число сигналов здесь – нечетная степень двойки:
21
2
K
M
+
=
. Не-
трудно убедиться, что максимальная и средняя энергии определяются как
2
31
1
632
c
d
EM
⎡
⎤
=
−
⎢
⎥
⎣
⎦
2
113 5
232 4 2
m
M
Ed M
⎡
⎤
=+−
⎢
⎥
⎣
⎦
, ,
32Mβ=
а средняя вероятность ошибки на символ (
)
2
1
2
0
1
1
1
0
1
1
00
4211212
,4
22
22 16
41 ,2 1
22
811
,,
22
e
j
j
d
PQT Q
MM
NM
d
QT j
MM
MN
jd j jd j
TT
Mjj
NN
β
β−
=
β−
=
⎡⎤
⎛⎞
ββ−
⎡⎤
⎢⎥
=− −−+
⎜⎟
⎢⎥
⎜⎟
β
⎢⎥
⎣⎦
⎝⎠
⎣⎦
⎡⎤
⎛⎞
⎛⎞
⎢⎥
+− + + ++
⎜⎟
⎜⎟
⎜⎟
⎢⎥
⎝⎠
⎝⎠
⎣⎦
⎡⎤
⎛⎞⎛⎞
+−
⎢⎥
+−
⎜⎟⎜⎟
⎜⎟⎜⎟
⎢⎥
⎝⎠⎝⎠
⎣⎦
∑
∑
.
+
)
(
,Ta
ν
Здесь
при , – функция Оуэна, 0a ≥0
ν
≥
()
()
2
2
2
0
11
,exp1
22
1
a
v
Tva t dt
t
⎡⎤
=−+
⎢⎥
π
+
⎢⎥
⎣⎦
∫
.
13

Отсюда следует, что точная формула средней вероятности ошибки
в M-ичном символе при оптимальном когерентном приеме двумерных
сигналов КАМ-32 по правилу максимального правдоподобия в канале с
детерминированными параметрами и аддитивным белым шумом
00
11
22623
88
22 2
e
dd d
PQ Q Q
NN N
⎡⎤
⎛ ⎞⎛⎞ ⎛⎞
⎢⎥
=+−
⎜ ⎟⎜⎟ ⎜⎟
⎜ ⎟⎜⎟ ⎜⎟
⎢⎥
⎝ ⎠⎝⎠ ⎝⎠
⎣⎦
0
,
где
2
17
2
m
Ed= , ,
2
5
c
Ed=
222
0
5
17 17 10 2
2
mbmc
hhhh
d
N
== ==
2
bc
.
Рис. П4.2
При манипуляционном коде, представленном на рис. П4.2, вероят-
ности ошибки на биты:
()
14 13
31
84
bb
PP QQ Q== ++
5
,
()
()(
21 3579
1357 1357 9
1
2
1
32
8
b
PQ QQQQ
QQQQ QQQQ Q
=+ ++− −
−+++ +++−
)
,
14
()()()
()(
3 1 39 1935
13571357
71 1
6
88 8
1
22 ,
8
b
PQ QQ QQQQ
QQQQ Q QQQ
)
=
+−+− +
−+++ +−−
−
()()()(
()( )
2
5 1 3 57 1559 37
13 13579
1
10 3 5
8
2.
b
PQQQQQQQQQQ
QQ QQQ QQ
⎡
=+−+−−−−−
⎢
⎣
⎤
−+ −−+−
⎥
⎦
)
−
5
1
1
5
b
i
P
=
=
bi
P
∑
Средняя вероятность ошибки
равна соответственно
()
()
() ()
()
2
2
13579 1 3
22
5713579
35 7 9 79
31 19 3 1 3 7 3
40 40 40 8 20 40 40
11 1131
40 40 5 10 20 10
11
.
20 20
b
PQQQQQ Q Q
QQQQQQQ
QQ Q Q QQ
=+++−− −
⎛⎞
+−−++−−
⎜⎟
⎝⎠
−+−+
+
Сигналы КАМ с периметром типа «крест» с нецелым числом
бит.
Для другой модификации КАМ «крест», когда
32
K
M
=
⋅
, (не-
целое значение
3K >
2
log
M
), средняя энергия
()
2
2
47 48 1
, 2 1;
6
1
, 2
6
c
M
dK
E
M
dK
⎧
−
⎡⎤
m
m
=
+
⎪
⎢⎥
⎪
⎣⎦
=
⎨
−
⎡⎤
⎪
=
⎢⎥
⎪
⎣⎦
⎩
и максимальная энергия
2
2
41 2 1 3 1
,2
96 3 12 2 2
51
,2
12 12 3 2
m
MM
dM Km
E
MM
dM Km
⎧
⎡⎤
⎛⎞
1;
.
−
++=
⎪
⎢⎥
⎜⎟
⎜⎟
⎪
⎢⎥
⎝⎠
⎪⎣ ⎦
=
⎨
⎡⎤
⎛⎞
⎪
−++ =
⎢⎥
⎜⎟
⎪
⎜⎟
⎢⎥
⎝⎠
⎪
⎣⎦
⎩
+
Вероятность ошибки в символе в этом случае
00
42 2
41
23
e
dd
PQ Q
MM
NM
⎛⎞ ⎛⎞
ρη⎡⎤
2N
=
++−
⎜⎟ ⎜⎟
⎢⎥
⎜⎟ ⎜⎟
⎣⎦
⎝⎠ ⎝⎠
−
15
2
00
38
41 ,
22
dd
QT
MM M
NN
⎛⎞⎛
λρ
⎛⎞
−+− − +
⎜⎟⎜
⎜⎟
⎜⎟⎜
ρ
⎝⎠
⎝⎠⎝
1
⎞
ρ−
⎟
⎟
⎠
11
11
00
16 8 1 1
,2 1 , ,
222
jj
djdjj
Tj T T
MMj
NN
ρ− ρ−
==
0
dj
j
N
⎡
⎤
⎛⎞⎛⎞⎛
+−
⎞
⎢
⎥
+++ −
⎜⎟⎜⎟⎜
⎜⎟⎜⎟⎜
⎟
⎟
⎢
⎥
⎝⎠⎝⎠⎝
⎠
⎣
⎦
∑∑
,
1
46
M
ρ=
1
23
M
ρ=
32η=
, если K нечетно, и , где 52λ= , , 8
λ
= ,
, если K четно.
3η=
2
23
6
c
Ed=
2
13
2
m
Ed=
24
M
=
3K
=
Если
, т. е. , то в этом случае ,
и вероятность ошибки в символе равна
2
00 0
2
00 0
121
31
36
22 2 2
1217
3.
36
22 2
e
dd dd
PQ Q Q Q
NN N N
ddd
QQ Q
NN N
⎡⎤
⎛⎞⎛⎞⎛⎞⎛⎞
⎢⎥
=−++
⎜⎟⎜⎟⎜⎟⎜⎟
⎜⎟⎜⎟⎜⎟⎜⎟
⎢⎥
⎝⎠⎝⎠⎝⎠⎝⎠
⎣⎦
⎛⎞⎛⎞ ⎛⎞
=+ −
⎜⎟⎜⎟ ⎜⎟
⎜⎟⎜⎟ ⎜⎟
⎝⎠⎝⎠ ⎝⎠
0
=
П4.1.5. Сигналы квадратурной амплитудной модуляции,
используемые в современных модемах
1. Согласно рекомендации протокола V.29 в модемах используются
сигналы КАМ-16 с четырьмя градациями амплитуды и восемью градация-
ми фазы (рис. П4.3, а), для которых
22
c
25 27
,
48
m
EdE==d
c
2
2
2
533
m
E
E
d ==
и .
Вероятность ошибки на символ в таком случае вычисляется по формуле
e
000
000
22
000
1351213
,,,
2422 22
2222
31513113
4222222
222 2
1153
4222
222
dddd
PT T T T
NNNN
ddd d
QQ Q Q
NNN
ddd
QQ Q
NNN
⎛⎞⎛ ⎞⎛⎞⎛
=+ ++
⎜⎟⎜ ⎟⎜⎟⎜
⎜⎟⎜ ⎟⎜⎟⎜
⎝⎠⎝ ⎠⎝⎠⎝
⎛⎞⎛ ⎞⎛ ⎞⎛ ⎞
++ + +
⎜⎟⎜ ⎟⎜ ⎟⎜ ⎟
⎜⎟⎜ ⎟⎜ ⎟⎜ ⎟
⎝⎠⎝ ⎠⎝ ⎠⎝ ⎠
⎛⎞⎛ ⎞⎛ ⎞
−− −
⎜⎟⎜ ⎟⎜
⎜⎟⎜ ⎟⎜
⎝⎠⎝ ⎠⎝ ⎠
0
0
1
,
3
N
⎞
+
⎟
⎟
⎠
−
0
.
2
d
Q
N
⎛⎞
⎟⎜ ⎟
⎟⎜ ⎟
⎝⎠
2. Для КАМ-8 (рис. П4.3, б) вероятность ошибки на символ
16
e
00 0
12 2
21
2
22 22
dd d
PQ Q Q Q
NN N
0
d
N
⎡
⎤⎡
⎛⎞⎛⎞⎛⎞⎛⎞
⎤
⎢
⎥⎢
=−+ −
⎜⎟⎜⎟⎜⎟⎜⎟
⎜⎟⎜⎟⎜⎟⎜⎟
⎥
⎢
⎥⎢
⎝⎠⎝⎠⎝⎠⎝⎠
⎥
⎣
⎦⎣
,
⎦
c
22
m
dE E==
где
3.
3. Для второго варианта КАМ-8 (рис. П4.3, в) вероятность ошибки
на символ
2
e
00
912
2
42
22
dd
PQ Q Q
NN
⎛⎞⎛⎞⎛⎞
=+−
⎜⎟⎜⎟⎜⎟
⎜⎟⎜⎟⎜⎟
⎝⎠⎝⎠⎝⎠
0
2
d
N
,
c
232
m
dE E==где 5.
64M
=
4. Следующая сигнальная конструкция, состоящая из сиг-
налов, построена на основе квадратной решетки с внешними точками,
сдвинутыми по оси координат. Использовалась в модеме Paradyne при
скорости передачи 14,4 кбит/с [2, с. 591, рис. 9.18, а]. Вероятность ошибки
на символ здесь
e
00 0
000
2
00 0
131135
,3 , ,
28 4
22323
11311747
,3 3 , , 3
44416
2232
171 247
,
81616
22 2
dd d
PT T T
NN N
ddd
TTT Q
NNN
ddd
QQQ
NN N
⎛⎞⎛⎞⎛⎞
=+++
⎜⎟⎜⎟⎜⎟
⎜⎟⎜⎟⎜⎟
⎝⎠⎝⎠⎝⎠
⎛⎞⎛⎞⎛⎞⎛
+−−+
⎜⎟⎜⎟⎜⎟⎜
⎜⎟⎜⎟⎜⎟⎜
⎝⎠⎝⎠⎝⎠⎝
⎛⎞⎛⎞ ⎛⎞
++ −
⎜⎟⎜⎟ ⎜⎟
⎜⎟⎜⎟ ⎜⎟
⎝⎠⎝⎠ ⎝⎠
0
2
d
N
⎞
+
⎟
⎟
⎠
17
где
c
42
313 7 3
d
E
m
2
73
E
d =
+
.
,
=
+
П4.2. Системы с многопозиционной фазовой модуляцией
Основная цель исследования, результаты которого представлены в
этом пункте, состояла в получении новых точных формул для расчета
матрицы переходных вероятностей и вероятности ошибки в M-ичном сим-
воле , в битах ,
1,iK=
e
P
bi
P и средней вероятности ошибки в бите для
классических двумерных сигналов с ФМ-M,
b
P
2
K
M
=
(PSK – Phase Shift
Keying). Практически все формулы получены впервые, другие – в новой
форме, и все формулы – для любого требуемого M, указанного выше.
Рассматривается канал с детерминированными параметрами и ад-
дитивным белым шумом [1, 2]. Предположим, что задана система сигна-
лов с фазовой модуляцией. Определим для этого случая одномерные ус-
ловные вероятности при оптимальном когерентном приеме
()(
**
ij j i i j
pr r pr rπ= = →
)
0, 1iM
=
−
, где ,
i
r – переданные M-ичные
символы,
j
r
∗
0, 1jM=−
, – принятые по ним решения. Тем самым найдем
матрицу переходных вероятностей
ij
Π
=π . Полученная матрица может
быть применена для решения широкого класса задач, например, для вы-
числения пропускной способности дискретного канала, вероятностей
ошибки на символ или на бит при произвольном манипуляционном коде,
определения среднеквадратичной ошибки приема непрерывных сообще-
ний в цифровых системах передачи и т. д.
П4.2.1. Матрица переходных вероятностей
1, 1jM
=
−
Используя результаты [8, 9] можно доказать, что ( )
22
00
1 2 sin 2 2 sin , ctg
jj m m
Qh Th
M
MM
π
ππ
⎛⎞⎛
π=π=− −
⎜⎟⎜
⎝⎠⎝
⎞
⎟
⎠
. (П4.5а)
[]
1, ent ( 1) 2jM=−
Кроме этого, при
18
() ()
() ()
() ()
22
0
2
2
21 21
1
2sin 2sin
2
21 21
2 sin ,ctg
21 21
2 sin ,ctg ;
jm m
m
m
jj
Qh Qh
MM
jj
Th
MM
jj
Th
MM
⎧⎫
−π +π⎛⎞⎛
⎪⎪
π= − +
⎜⎟⎜
⎨⎬
⎪⎪
⎝⎠⎝
⎩⎭
⎧
−π −π⎛⎞
⎪
+−
⎜⎟
⎨
⎪
⎝⎠
⎩
⎫
+π +π⎛⎞
⎪
−
⎜⎟
⎬
⎪
⎝⎠
⎭
⎞
⎟
⎠
(П4.5б)
22
0, 2
2sin 2 2sin,ctg
Mm m
Qh Th
M
MM
π
ππ
⎛⎞⎛
π= −
⎜⎟⎜
⎝⎠⎝
⎞
⎟
⎠
, (П4.5в)
[]
ent ( 1) 2 1, 1jM M=−+
а при
−
00,
j
Mj
−
π
=π
. (П4.5г)
Выражение (П4.5в) используется только при четном значении M. Здесь
2
0
mm m
hENPTN==
0
, где и соответственно мощность и энергия
сигналов ФМ-M, – односторонняя спектральная плотность мощности
белого шума. Пусть
m
P
m
E
0
N
2
2sin
km
k
QQ h
M
π
⎛⎞
=
⎜⎟
⎝⎠
2
2 sin ,ctg
km
kk
TT h
M
M
π
π
⎛⎞
=
⎜⎟
⎝⎠
, .
Используя геометрическое представление сигналов ФМ-M, можно
убедиться, что матрица переходных вероятностей относится к классу матриц
теплицева типа, является симметричной относительно двух главных диагона-
лей, в частности,
,0, ,1,21ij M
=
−ij M 1
ij ji
π
=π
=
−
, ,
0,
ij
ij
, : π=π
−
00 01 02 0, 1
01 00 01 0, 2
02 01 00 0, 3
0, 1 0, 2 0, 3 00
...
...
...
... ... ... ... ...
...
M
M
M
MM M
−
−
−
−− −
πππ π
⎛⎞
⎜⎟
πππ π
⎜⎟
⎜⎟
πππ π
Π=
⎜⎟
⎜⎟
⎜⎟
ππ π π
⎝⎠
.
Как уже отмечалось, данная матрица может использоваться для ре-
шения многих прикладных задач. Воспользуемся ею для вычисления пропу-
скной способности дискретного канала и вероятности ошибки на символ.
П4.2.2. Пропускная способность дискретного канала
Дискретный канал называется симметричным по входу, если все
строки матрицы переходных вероятностей Π образованы перестановками
19

элементов первой строки, и симметричным по выходу, если все столбцы
матрицы Π образованы перестановками элементов первого столбца [4].
Дискретный канал называется симметричным, если он симметричен и по
входу и по выходу. Нетрудно убедиться в том, что данный дискретный
канал является симметричным. Пропускная способность C, бит/с, симмет-
ричного дискретного канала без памяти равна [4]
1
202
0
log log
M
0
j
j
j
CV M
−
=
⎛⎞
⎜
=+π
⎜
⎝⎠
∑
⎟
π
⎟
, (П4.6)
0
j
π
где
– элементы первой строки матрицы переходных вероятностей и
1V= T – скорость передачи символов по каналу связи (число символов в 1 с).
П4.2.3. Свойства пропускной способности дискретного канала
с учетом свойств непрерывного канала
При фиксированных значениях , можно так изменять ско-
рость передачи V и соответственно длительность канальных символов T,
что будет обеспечиваться наибольшая пропускная способность канала
связи в единицу времени C, что согласно теореме кодирования обеспечит
наибольшую скорость передачи V сообщений источника при сколь угодно
высокой верности приема. Таким образом, данная задача может быть
формально записана как [5, 6]
m
P
0
N
()
2
2
2
0
1
202
2
0
0
max max
1
max log log
m
m
m
V
h
m
M
m
jj
h
j
m
P
CV C
hN
P
M
N
h
−
=
⎛⎞
==
⎜⎟
⎜⎟
⎝⎠
0
⎧
⎫
⎪
⎪
=+π
, (П4.7)
π
⎨
⎬
⎪
⎪
⎩⎭
∑
2
0
mm
VPhN=
так как
.
Можно убедиться в том, что при уменьшении длительности сигнала
(
)
V →∞
0T → пропускная способность монотонно возрастает, несмот-
ря на уменьшение величины
2
0
mm m
hPTNPVN==
0
. Поэтому максимум
может быть найден в этом случае, например, численными методами. Ана-
литический подход требует более сложных расчетов. Однако в этом слу-
чае можно воспользоваться, тем, что максимум достигается при
0T →
20
(
)
V →∞
и, следовательно, при . Для этого вместо точных фор-
мул можно использовать асимптотические, а именно: при
2
0
m
h →
0x →
()
()
()
22
1
1
10
arctg
1
,
22 2
2!
kj
k
j
k
k
kj
a
xa
Txa C
j
k
+
∞−
−
==
1
1
⎡
⎤
⎢
⎥
≅+
π
π+
⎢
⎥
−
⎣
⎦
∑∑
, (П4.8а)
()
3
1
...
2
262
xx
Qx
=
−+ −
ππ
(П4.8б)
Тогда
()
2
1
202
2
0
0
0
1
max lim log log
m
M
m
0
j
j
V
h
j
m
P
CV M
N
h
−
→
=
⎧
⎫
⎪
⎪
=+π
π
⎨
⎬
⎪
⎪
⎩⎭
∑
. (П4.9)
Используя (П4.8) можно доказать, что
()
()
2
0
0
max sin c , 3 ;
4ln2
2
max , 2.
ln 2
m
V
m
V
P
CV M
MN
P
CV M
N
ππ
⎛⎞
=
≥
⎜⎟
⎝⎠
==
π
(П4.10)
Отметим, что
()
2
lim
1, 2337...
28
M
C
CM
→∞
π
==
=
(П4.11)
Можно сделать несколько выводов.
Во-первых, максимум пропускной способности дискретного канала
при когерентном приеме многопозиционных сигналов достигается при
неограниченной полосе пропускания, так как при
(
)
V →∞
0T → поло-
са пропускания приемника .
F →∞
Во-вторых, переход от двоичных сигналов к многопозиционным
увеличивает пропускную способность только в
2
8π
1
M
>>
раз (при , см.
(П4.11)).
В-третьих, пропускная способность данного дискретного канала
уменьшилась в
2
4
sin c
M
−
π
⎛
⎜
π
⎝⎠
2
π
⎞
⎟
4
M
≥ 2
M
=
раз при и в раз при по
21
