Бромберг П.В. Теория инерциальных систем навигации

Подождите немного. Документ загружается.

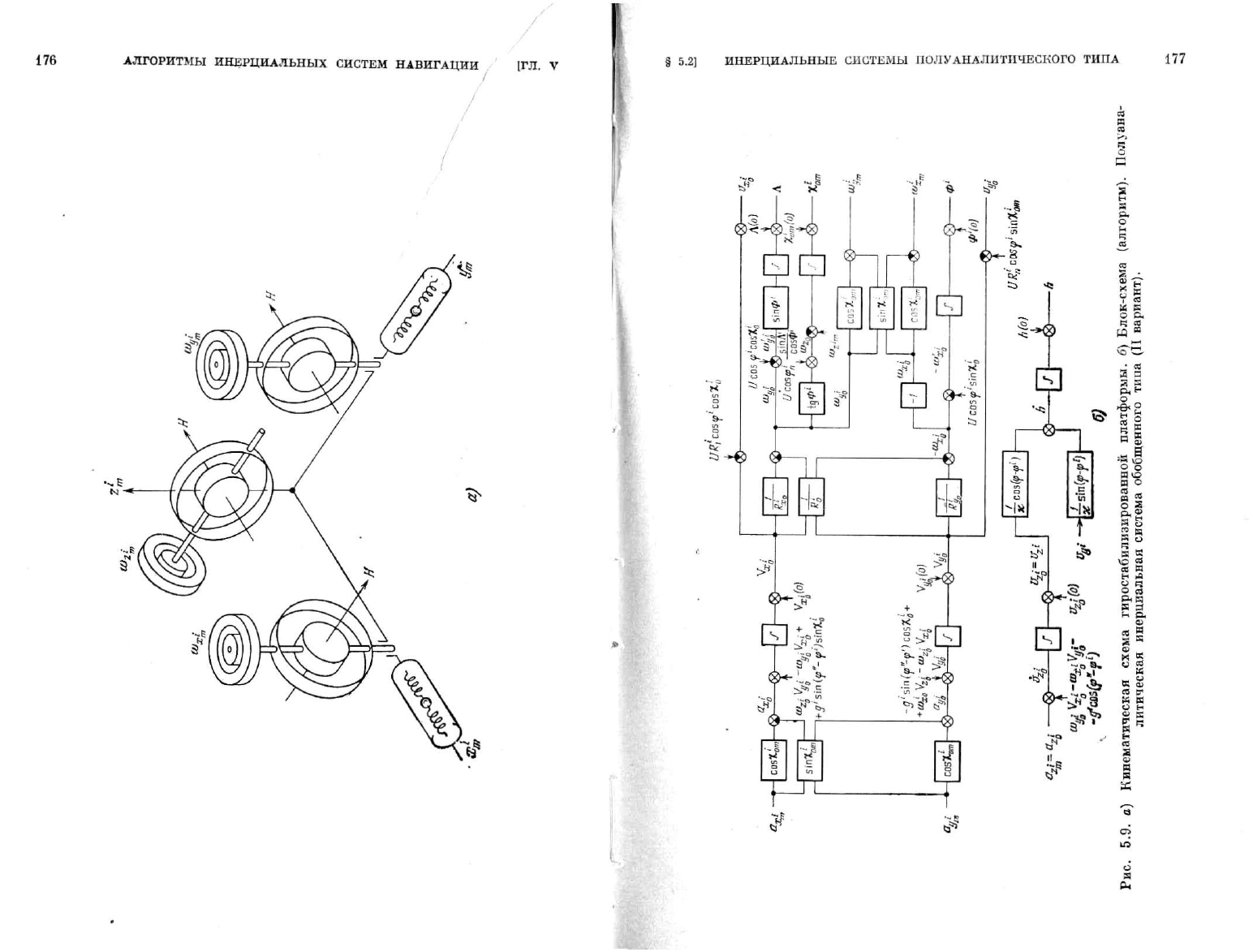
§ 5.2] ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ПОЛУАНАЛИТИЧЕСКОГО ТИПА

177

178

ЛЛГОГИТМЫ ИНЕРЦИАЛЬНЫХ СИСТЕМ НАВИГАЦИИ

[ГЛ.

координат. Дальше

для

определения координат можно поступить

в соответствии

моделирующей схемой, представленной

на

рис.

5.9.

Несколько иначе здесь образуются величины

<в $ и о> *,

"о

необходимые

для

управления платформой.

Они

находятся

по

(5.48) при

замене

в них

индекса

о на

индекс

с.

5.3.

Инерциальные системы аналитического типа

При решении задач околоземной павигации

за

инерциальную

систему координат

мы

приняли систему £

н„£

началом

центре

Земли, осью

£д,

направленной вдоль полярной

оси

Земли

к Се-

верному полюсу,

осями

§„., Г|

лежащими

плоскости парал-

лельной плоскости экватора

и не

участвующими

суточном вра-

щении Земли. Соответствующий этой системе координат ииер-

циальный трехгранник £

т)

примем

за

опорный.

Первый вариант алгоритма.

первом вариан-

те алгоритма

он

будет служить также навигационным трехгран-

ником. Трехгранник

т)

не

вращается

абсолютном простран-

стве,

поэтому проекции

, tOr^, юг его

абсолютной угловой ско-

рости

на

ребра

, т)

, £

равняются нулю,

т. е.

®t

= {)

> °Ч = 0,

«>t

= Q- (5.46)

Рассматриваемая здесь инерциальная навигационная система

должна принципиально содержать

три

акселерометра, измери-

тельные

оси

которых номинально направлены вдоль осей

Пд,

Проекции кажущегося ускорения

а^, а

Лд

, og

на оси |

4ai tai

идеальном случае измеряемые акселерометрами, опре-

деляются

(3.43).

Разрешая равенства

(3.43)

относительно произ-

водных скорости, получим выражения

ta =

Еа + ft.'

(5.47)

в которых проекции гравитационного ускорения представляются

по формулам

(3.46) в

виде

*%£

•

ft = — g —-f-3pg

С (£

+ri

)E;

—-3pg ^ .

= /Й + tiJ + fi, • (5.48)

5.3]

ИНЕРЦИАЛЬНЫК СИСТЕМЫ АНАЛИТИЧЕСКОГО ТИПА

179

а определяется первой формулой (1.74а)

при

замене

в ней £

на

, т. е.

g'-i~^(l-p;4-)-

(5.49)

копстанты имеют следующие значения:

[3' =

1,437-Ю"

6378,245

км, =

981,438

см/с

Формулы счисления прямоугольных координат

, т]

, £

в соответствии

с (1.118)

имеют

вид

ta = V

, i = F

£„ = TV (5.50)

Уравнения

(5.47) с

учетом

(5.48) и (5.49) и

уравнения

(5.50)

обра-

зуют совокупную систему обыкновенных дифференциальных

уравнений шестого порядка.

этой системе

а^, о , at

измеря-

емые акселерометрами, являются известными функциями вре-

мени, решение системы, удовлетворяющее заданному начальному

условию

la (0), r,

(0), t

(0), V

(0), V„

(0), V

(0),

определяет

текущие координаты

(t), r\

(t), £

(l)

точки

местоположения

объекта

компоненты

(t), V

(t), (t)

абсолютной скорости

его движения. Естественно, начальные условия должны опреде-

лять коордипатьг точки

М и

компоненты скорости движения

объекта

при t = 0. Эти

величины

не

определяются инерциальной

навигационной системой,

они

вносятся

инерциальную систему

по источникам внешней информации.

Моделирующая схема рассматриваемой инерциальной системы

представлена

на рис. 5.10. По

этой схеме опорный трехгранник

материализуется свободной гиростабилизироваппой платформой,

т.

е.

платформой,

на

датчики моментов гироскопов которой

не

подаются управляющие сигналы. Кроме того, гироплатформа

здесь должна иметь дополнительную следящую раму

для

предотвра-

щения складывания

рам

кардапова подвеса.

Гироплатформа сохраняет неизменную ориентацию относи-

тельно неподвижных звезд

непрерывно меняет свою ориентацию

относительно земных ориентиров. Если начальную выставку

платформы осуществлять

по

земным ориентирам,

то

нужно либо

оговорить время запуска системы, либо необходимо осуществить

непрерывное отслеживание платформой (заранее вычисленное

запрограммированное) изменяющегося положения относительно

земных ориентиров.

В рассматриваемом случае может появиться необходимость

в определении вторичных координат

*), за

которые

мы

примем

Под

первичными координатами

понимаются координаты, получаемые

в инерциальной системе интегрированием;

вторичные координаты

получают-

ся

из

первичных

шшощьто конечных формул преобразования координат.

180

АЛГОРИТМЫ

ИНЕРЦИАЛЬНЫХ СИСТЕМ НАВИГАЦИИ

[ГЛ. V

географическую долготу

географическую широту

ср и

высоту

/г,

а также проекции относительной скорости

на

ребра географиче-

ского трехгранника

xyz. Эти

величины получаются

из

ранее най-

денных посредством конечных формул преобразования.

Эти

фор-

мулы можно получить

из

следующих соображений. Таблицу коси-

нусов углов между осями

х, у, z и |

, г|

, £

можно получить

из

(о)

-г-

Рис.

5.10. а)

Кинематическая схема гиростабвяизированой платформы.

б)

Блок-схема (алгоритм). Аналитическая инерциальная система

инер-

циальным

опорным трехгранником.

(1.76),

если

там X

заменить

на Х

, а оси |, Т], £ на |

, т)

, £

, В

част-

ности, направляющие косинусы

оси z по

отношению

осям

£„,

ча>

Со

соответственно равны

cos ср cos Х

, cos ф sin Х

, sin ф.

Вектор ускорения силы тяжести;/ направлен вдоль отрицательной

полуоси

поэтому

- — g cos

ср

cos Ь

, g

= — g cos ф sin Х

Ь%

= £ sin ф.

(5.51)

Сравнивая формулы

(5.51) и (3.49) (в

последних только нужно

5.31

ИНЕРЦИАЛЬНЫЕ

СИСТЕМЫ АНАЛИТИЧЕСКОГО ТИПА

181

Т),

'С,

заменить

на \

, чя> £а)>

получим выражения

со?

ф cos Х

—

cos

ср

sin Х

—2а

- 2а-

(5.52)

sin

ср

—-

~у- \

-f 2а

Из формул (1.118а) непосредственно находим соотношения

cosX„

—

sin

—

•

Vil

(5.53)

Обычно стремятся углы находить

по их

тангенсам.

нашем слу-

чае

ф и Х

можно определять формулами

= (l + 2a) is

Х„

(5.54)

Первая формула

(5.54)

получается

из (5.52),

если сначала

из

пер-

вых двух выражений определить

cos ф и с

помощью третьего

выражения сформировать

tg ср,

после чего разложить члены,

со-

держащие

а, в

биномиальный

ряд и

отбросить слагаемые

с а

и более высокого порядка малости.

Второе выражение

(5.54)

пепосредствепно получается

из (5.33).

(5.54)

знак

совпадает

со

знаком координат

квадрант

угла

находится

по

сочетанию знаков координат

т|

и £

(см.

(5.33)).

Географическая долгота

находится

по

формуле

= Х

— ut,

(5.54а)

где время

отсчитывается

от

момента прохождения гринвичского

меридиана через плоскость

(см. н. 1.3.6). По

формулам

(5.52)

(5.53)

можно выразить направляющие косинусы осей

х, у, z

относительно осей

, т|

, 'С,

через прямоугольные координаты

мот £а-

Тогда

соответствии

(1.76) проекции

, V

абсолютной скорости

на оси х, у, z

находятся

из

следующих формул

преобразования:

(5.55)

= — V

sin X

+ Кц

cos Х

= — V%

cos X

sin ф — Vf]

sin X

sin

ф•

-\~

V$ cos ф,

= V%

cos X

cos

+ Vr\ sin X

cos ф

-]-

sin ф.

Проекции

, v

относительной скорости определяются равен-

182

АЛГОРИТМЫ ИНЕРЦИАЛЬНЫХ СИСТЕМ НАВИГАЦИИ

[ГЛ. V

ствами

- UVfa + 5. Щ V* V* =

г- (5-56)

Высоту

можно найти

из (1.17),

если

там siu ф'

заменить отно-

шением

к г.

Таким образом получим

h = а

+ =

- Vg + тй

-1-

(1 + 7) Й. (5.57)

И наконец, следует определить ориентацию объекта

про-

странстве. Ориентацию объекта

пространстве будем определять,

как

прежде, углом истинного курса

углом тангажа

т} и

углом крена

уз-

Свяжем

объектом систему координат

XYZ,

причем

ось Y

направлена вдоль

его

продольной

оси

вперед,

ось Z

выберем

пло-

скости продольной симметрии

так,

чтобы

она

была перпендикуляр-

на

оси Y и

направлена вверх

при

нормальном положении объекта,

ось X

определяется

тем

обстоятельством,

что

трехгранник

XYZ

должен иметь правую ориентацию.

Оси X, У, Z

можно назвать

поперечной, продольной

нормальной осями объекта.

качестве

базового трехгранника

для

определения углов

, r>, Vs

возь-

мем географический трехгранник

xyz.

Пусть сначала трехгран-

ники

XYZ и xyz

совпадают друг

другом. Тогда связанный трех-

гранник

XYZ

может быть переведен

произвольное положение

относительно трехгранника

xyz

тремя последовательными незави-

симыми поворотами: сначала

па

угол

вокруг отрицательного

направления

оси Z (т. е. с

положительного конца

оси Z

вращение

будет происходить

по

часовой стрелке), затем вокруг промежуточ-

ного положения

оси X на

угол

# и.

наконец, вокруг окончатель-

ного положения

оси Y на

угол

Такую последовательность

по-

воротов

мы

рассматривали

в п.

3.5.1. Поэтому преобразование

гистем координат

xyz в XYZ мы

получим

из (3.124) и (3.126),

заменив

там оси х

, у

Р1

на оси X, Y, Z

соответственно

поло-

жив

у-, = t), у

?s> Yn

—

Фк- Таким образом получим

х -

Z _

(5.58)

Элементы матрицы

Ск

следующие:

cj"

= cos ys

cos

Фк

+ sin ys sin

sin ф

Скг*

= — cos

Ys sin ф

+ si'

$ sin Ys

C0R

^к»

Скг

= — cos О sin Ys, cSr = cos т) sin ф

cjj

= cos f) cos ф

, cS* = sin 0,

6.3]

ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ АНАЛИТИЧЕСКОГО ТИПА

183

Сиг

= sin

cos ф

— sin # cos

sin фк,

—

— sin

sin ф

— sin 0 cos

cos ф

cif?

= cos 0 cos ys-

В соответствии

принятыми

в п. 3.4.3

обозначениями полученную

матрицу преобразования географической координатной системы

xyz в

связанную

XYZ

обозначили через

кг

Элементами матрицы

кт

служат косинусы углов между осями систем

XYZ и xyz.

Из

(5.58)

можно получить равенства

Sind

= cos (Y z) *), tg

cos (Y x)

—

cos (X '.

cos

[;

cos (Y y)

(5.59)

по которым можно определить углы

f},

Ys и ф

Для определения элементов матрицы

кг

построим

два

орто-

гональных преобразования:

(5.60.)

—

Па

П.

—

Та

Па

(5.61.

Сравнивая

три

ортогональных преобразования

(5.58), (5.60) и

(5.61),

получим матричное равенство

Скг^га

~ C

. (5.62)

Если умножить матричное равенство справа

на

транспонирован-

ную матрицу

Сра, то,

замечая,

что Cl

= C^l,

получим

КГ

— С

га

= C%

. (5.63)

Матрица

С1

определяет ортогональное преобразование географи

ческой системы

xyz в

инерциальную систему £

%£а

(

поэтому

мы

ее обозначили через

аг

Элементы матрицы

аг

определяются

таблицей

(1.76) при

замене

Хна %

и |, и, ^ на |а,

ма

, £;

; они

выра-

жены раньше через найденные координаты

х\

, t,

Преобразования

(5.60)

можно построить (аналогично преобра-

зованию

(5.58))

тремя последовательными поворотами связанного

Yz —

угол между осями

У иг,

184

АЛГОРИТМЫ ИНЕРЦИАЛЬНЫХ СИСТЕМ НАВИГАЦИИ

[ГЛ, V

трехгранника

XYZ из

положения,

котором

он

совпадал

инер-

циальным трехгранником |

г|

. Инерциальный трехгранник

lo^o?"

материализуется стабилизированной платформой. После-

довательные повороты вокруг

оси Z,

промежуточного положения

оси

X и

окончательного положения

оси Y на

углы

, у

будут

происходить вокруг материальных осей (обозначим

их 3, 1, 2)

кардановых

рам

подвеса. Указанные углы измеряются соответ-

ствующими датчиками. Матрица суммарного поворота

ка

сов-

падает

матрицей

(3.126).

Таким образом, элементы матриц

ка

Cat

определяются

по

измеренным углам

, Уз и

расчетным

значениям координат

, ф или

даже первичных координат

£«,

т|а»

Со- Перемножая

эти

матрицы, найдем

по (5.63)

элементы мат-

рицы

кг

(5.58), а

следовательно,

направляющие косинусы,

фигурирующие

равенствах

(5.59). Из

последних равенств нахо-

дим углы

т>, ys,

Фк,

определяющие ориентацию объекта.

Второй вариан

алгоритма. Рассмотрим вто-

рой вариант алгоритма навигационной системы

инерциальным

опорным трехгранником.

качестве навигационного трехгран-

ника выберем географический трехгранник

xyz,

следовательно,

за первичные координаты

—

географические долготу

Ха

широту

ф.

Высоту

определять здесь

не

будем. Опорным трехгранником,

как

прежде, будет служить инерциальный трехгранник

По проекциям

щ , а

Ца

, а^

кажущегося ускорения, непосредственно

измеряемым акселерометрами, находим проекции

, а

ка-

жущегося ускорения

на оси

географической координатной систе-

мы

xyz.

Формулы преобразования имеют

вид

х~

sin Х

cos X

0 "

—

sin ф cos X

—

sin

sin %

COS

cos ф cos X

cos ф sin X

sin ф

ta.

Матрица преобразования получается транспонированием таблицы

(1.76) и при

замене

в ней X на Х

и |, ц, t, на

, T|

Найденными проекциями

, а

, а*

можно распорядиться

в со-

ответствии

алгоритмом, рассмотренным

в п.

5.2.1,

и на

выходе

инерциальной системы получить

X, ф и v

, v

. По

географической

долготе

следует определить абсолютную долготу

необходимую

для формирования матрицы преобразования

(5.64). Для

этой

цели используем формулы (5.54а),

(5.59).

Ориентация объекта

определяется

по

указанной выше процедуре, изложенной

первом

варианте алгоритма.

Читателю предлагается самостоятельно построить алгоритм

инерциальной системы аналитического типа, взяв

за

опорный

навигационный трехгранники экваториальный трехгранник

|п,£,

жестко связанный

Землей.

8 5.4]

БЕСПЛАТФОРМЕННЫЕ ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ

185

5.4.

Бесплатформенные инерциальные системы

—

ГУ

5.4.1. Инерциальная система

однокомпонентнымн гироизме-

рителя ми абсолютной угловой скорости.

бесплатформенных

инерциальных системах опорный трехгранник, который

мы

будем

обозначать через

XYZ,

жестко связан

объектом.

системах

данного типа акселерометры выдают информацию

проекциях

a.Y, ay, az

кажущегося ускорения

на

связанные

оси X, Y, Z.

Чтобы использовать

эту

информацию

для

решения задач навига-

ции, необходимо

каждый момент времени знать ориентацию

объекта

или, что то же

самое, трехгранника

XYZ

относительно

базовой системы отсчета.

В рассматриваемом случае ориентация трехгранника

XYZ

определяется

по

проекциям

его

абсолютной угловой скорости

(од-,

toy, o>z на оси X, Y, Z,

которые

измеряются тремя гироскопическими

датчиками абсолютной угловой скорос-

ти,

описанными

в § 4.4.

На

рис. 5.11

показано расположе-

ние измерительных осей акселеромет-

ров

гироизмерителей абсолютной

уг-

ловой скорости относительпо осей

Y, Z

опорного трехгранника.

В качестве базовой системы отсчета

рассмотрим сначала абсолютную систе-

^'V'

му координат

£а, т. е.

систему

координат, относительпо которой гиро-

скопические приборы измеряют угло-

Рис. 5.11.

Взаимное распо-

вую скорость опорного трехгранника ложоние связанной

с объ-

XYZ.

инерциальных системах нуншо

™

а™н„ГГ™

определить девять направляющих

ко-

координат

tiHata-

синусов осей

X, Y, Z

опорного трех-

гранника относительпо абсолютной системы координат

т|

So.

Эту задачу можно решить двумя различными путями.

Первый вариант алгоритма сводится

нахо-

ждению трех углов

Yi, у%, Y:t

последовательных, независимых

по-

воротов трехгранника

XYZ,

которые переводят трехгранник

XYZ

из

начального положения,

котором

он

совпадал

трехгран-

ником

f]at,

данное текущее положение. Последовательные

повороты будем проводить

следующем порядке. Сначала повер-

нем трехгранник

XYZ на

угол

вокруг первоначального поло-

жения

оси Z,

совпадающей

осью

затем повернем

на

угол

вокруг промежуточного направления

оси X и,

наконец, повернем

на угол

уг

вокруг нового направления

оси Y.

Последовательные повороты

взаимное положение трехгран-

ников

iau^t и XYZ

изображены

па рис. 5.11.

186

АЛГОРИТМЫ ИНЕРЦИАЛЬНЫХ СИСТЕМ НАВИГАЦИИ [ГЛ.

—

и.

Там показаны угловые скорости

, Уз в

виде векторов,

на-

правленных вдоль положительных направлений осей

X', У, £а-

Указанные

оси

образуют косоугольную систему координат

X' Y £

Преобразование координатных систем посредством трех последо-

вательных поворотов

по

указанной выше схеме рассматривалось

п.

3.5.1.

В нашем случае преобразование координатных систем опреде-

ляется

виде

(см.

также

(5.60))

(5.65)

Это преобразование получается

из (3.124)

заменой

xyz на

|„т|

на XYZ.

Ортогональная матрица преобразования^

Ка

определяется

(3.126).

Установим связь между величинами

, у

и о>у, «у, о>?;,

которые являются составляющими одного

того

же

вектора абсо-

лютной угловой скорости трехгранника

XYZ. Для

этой цели

найдем ортогональные проекции векторов, изображающих

уи

Уз, на оси

прямоугольной системы координат

XYZ. Эти

проек-

ции определяются через направляющие косинусы осей

X', У,

относительпо системы координат

XYZ,

направляющие коси-

нусы

осп X'

можно получить

из

первого столбца матрицы

(3.126),

если

там

положить

Уз

соответствующие косинусы

оси 1

определяются третьим столбцом

той же

матрицы,

направляющие

косинусы

оси У,

очевидно, равны

0, 1, 0

соответственно.

Таким образом,

(Ох

= ti

°s

— Тз cos yt sin y

coy = ta +

tasmvi,

toz =

SIN

cos

cos ya.

(5.66)

Разрешая

(5.66)

относительно

, у

получим

= «я cos

4- t»z sin y

fs - toy — tg yi (— ®х sb

cos ya),

Тз

COS

(—

sin

+ «

cos у

(5.67)

Соотношения

(5.67)

преобразуют составляющие

а>х,

0>зт,

®z

абсолютной угловой скорости связанного трехгранника

ХУ2

в производные

но

времени

от

углов поворота

? Ya-

Углы

Уз

могут быть получены

из (5.67)

интегрированием. Преобра-

зование

сах, сэу, &z в Yi,

YE,

гз

не

определено

при Yi = л/2. При

таком значении

повороты

на

углы

производятся вокруг

одной

и той же оси (оси £

), так как при Yi — п/2 ось У (У)

КЕСГГЛАТФОРМЕННЫЕ ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ

187

(см.

рис. 5.11)

совпадает

осью

. В

этом случае возникает

за-

труднение

раздельном определении углов поворота вокруг этих

осей,

т. е.

углов

и Уз-

В уравнениях

(5.67)

ОУ

о)

, «

считаются известными функция-

ми времени;

инерциальных системах

они

являются выходными

величинами гироизмерителей абсолютной угловой скорости.

Со-

отношения

(5.78)

представляют собой систему нелинейных

диф-

ференциальпых уравнений

переменными параметрами относи-

тельно искомых функций времени

(t), у

(t). Эти

уравне-

ния могут быть решены численными методами, если будут заданы

начальные условия,

т. е.

заданы величины

Yi (0), у

(0), уа (0),

соответствующие моменту времени

t = 0.

Углы

Yi (0), Ya (0)*

(0)

определяют ориентацию связанного трехгранника

XYZ

относительно инерциального £

г)а£«

£ = 0. В

системе

(5.67)

первые

два

уравнения являются связанными, последнее уравне-

ние решается квадратурой после того,

как

решения

(t) и у

(t)

будут найдены.

Определение углов ориентации

Ya> Y3

производится реше-

нием уравнений

(5.67) по

составляющим о>^-,

«у, o>z,

определяемым

гироизмерителями

начальными данными

Yi (0), у

(0), у

(0).

Определение углов

Yi (0), Ya Уз (0)

можно назвать началь-

ной выставкой связанного трехгранника

XYZ

относительно инер-

циального трехгранника

£,

По найденным величинам

Yn Ya* Y3 мы

мо;кем

по (3.126) по-

строить матрицу

ка

= C

фигурирующую

преобразовании

(5,76),

затем транспонированием найти матрицу обратного пре-

образования

ак

= Су- С

помощью матрицы

аК

мы

можем

по

проекциям

ах, a

, a

кажущегося ускорения

на оси X, У, Z,

которые непосредственно измеряются акселерометрами, найти

по

формуле

проекции

а|

, Оц^а^

ка?кущегося ускорения

на оси

инерциального

трехгранника

L-

После такой операции решение задач нави-

гации сводится

алгоритмам, рассмотренным

в п. 5.3.1 для

инер-

циальной системы аналитического типа.

Это

относится

опреде-

лению координат местоположения объекта

%, ц>,

компонент ско-

рости

его

движения

, щ и

ориентации объекта, определяемой

истинным курсом

углом тангажа •&

углом крена

Уравнения

(5.67),

определяющие связь между производными

углов поворота

Vu Y2? Y3

проекциями

toy, <a

абсолютной

угловой скорости связанного трехгранника, неудобны.

Они

явля-

ются нелинейными уравнениями

и не

обладают симметрией, кроме

188

АЛГОРИТМЫ ИНЕРЦИАЛЬНЫХ СИСТЕМ НАВИГАЦИИ

1ГЛ. V

того,

имеет место особый случай

при у

= л/2. От

таких недостат-

ков свободны уравнения

(3.107),

которые непосредственно опреде-

ляют направляющие косинусы, характеризующие взаимное рас-

положение двух координатных систем.

Второй вариант алгоритма основан

на

непо-

средственном определении элементов матрицы

а№

по

уравнениям

(3.107), в

которых теперь нужно считать

направляющими

ко-

синусами осей

X, Y, Z

относительно системы координат 1

£а>

а вместо

to*, ю

, ю

нужно писать

со*, ыу, со

- В

соответствую-

щее вычислительное устройство составляющие

сод-, coy, wz

вво-

дятся

гироизмерителей абсолютной угловой скорости, кроме

того,

него нужно ввести девять начальных значений направля-

ющих косинусов

(0) *).

Построив матрицу

aVt

следова-

тельно,

и С

ко

= Саю мы

получим возможность решить задачу

навигации

соответствии

рапее установленной процедурой.

Вторая процедура нахождения матрицы

аК

является более

гибкой,

т. е. она

позволяет

помощью обобщенных уравнений

(3.118)

определять направляющие косинусы связанных осей

Y, Z не

только относительно абсолютной системы координат

1аГ\

1а,

но

также относительно других систем отсчета.

Во

всех

случаях системой координат

фигурирующей

в (3.118),

будет служить

XYZ, а

систему коордипат

можно выбрать

по своему усмотрению.

При проектировании инерциальных систем пеобходимо про-

вести тщательный анализ различных вариантов схем

обязатель-

ным учетом процедуры начальной выставки

накопленного прак-

тического опыта, прежде

чем

выбрать схему

для

технической реа-

лизации.

Рассмотренные

данном пункте инерциальные системы

не

имеют

своем составе гир оставили зированных платформ. Гиро-

скопические измерители, установленные непосредственно

на

объекте, работают

более тяжелом режиме,

чем

гироскопы, уста-

новленные

на

гиростабилизированпой платформе.

Они

должны

измерять угловые скорости порядка угловой скорости Земли

7,29-10

-5

1/с и

угловую скорость вращения самолета вокруг

продольной

оси,

имеющей

для

некоторых самолетов порядок

400

град/с,

т. е.

порядок

рад/с. Таким образом, отношение мак-

симальной величины

минимальной составляет

7/7,29-10

Естественно,

большем диапазоне изменения измеряемых

величин труднее обеспечить заданную точность измерения.

5.4.2.

Инерциальная система

со

свободными гироскопами.

Во

второй разновидности инерциальных навигационных систем рас-

сматриваемого класса ориентация объекта

связанного

с ним

опорного трехгранника

XYZ

определяется двумя свободными

Эта

процедура была рассмотрена

а п.

3.4.3.

5.4]

БЕС ПЛАТФОРМЕННЫЕ ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ

189

гироскопами.

Оси

свободных гироскопов сохраняют неизменное

направление

инерциальной пространстве, поэтому

два

свободных

гироскопа могут смоделировать инерциальный трехгранник

и,

властности, трехгранник

Для

этого

ось

одного гироскопа

нужно направить параллельно

оси |

, а

другого

—

параллельно

оси

т|

направление третьей

оси (оси £

)

можно определить ана-

литически векторным произведением единичных векторов,

т. е.

выражением

£° = |" X г£.

Таким образом,

два

свободных гиро-

скопа могут создать

па

борту объекта базовую систему отсчета.

Электрические

(или

другого типа) датчики углового положения

свободных гироскопов обеспечивают непосредственное измерение

углов

, уд

ориентации трехгранника

XYZ,

жестко связанного

с объектом,

или его

направляющих косинусов

аК

относительно

абсолютной системы координат £

Ча£

По

измеренным значениям

углов

, уз или

направляющих косинусов

аК

проекциям

кажущегося ускорения

ах, a

, a

решение задачи навигации осу-

ществляется путем использования алгоритмов предыдущего пунк-

та

без

необходимости решения дифференциальных уравнений

(5.78) или (3.107), что

является достоинством бесплатформенной

инерциальной системы

со

свободными гироскопами

по

сравнению

с системой

однокомпонентными гироизмерителями абсолютной

угловой скорости.

В инерциальных системах данного типа могут быть исполь-

зованы электростатические

криогенные свободные гироскопы.

В таких приборах шаровой ротор взвешен

вакууме

при

помощи

электрических

или

магнитных полей.

последнем случае требуют-

ся условия сверхнизких температур

сверхпроводимости]

для

устранения потерь

от

вихревых токов, наводимых магнитпым полем

во вращающемся шаровом роторе.

На

практике стараются умень-

шить

вес

подвешиваемой массы путем создания полого ротора.

Электростатический

криогенный гироскопы нуждаются

под-

держании впутри герметичного корпуса прибора глубокого

ва-

куума

для

снижения моментов, тормозящих вращение ротора,

ко-

торый разгоняют

до

высокой скорости

оставляют вращаться

по инерции

течение всего времени работы.

Рассматриваемые гироскопы могут быть использованы

систе-

ме также

виде пространственного акселерометра.

Оба гироскопа оснащены двухкомпонентными датчиками съема

сигнала. Если двухкомпонентный датчик работает только

в ло-

кальной области,

то

свободный гироскоп требует применения

внешнего следящего карданова подвеса.

В свободном гироскопе

без

следящего подвеса

для

съема сиг-

налов применяют также систему оптических датчиков, считываю-

щих кодовый рисунок

на

поверхности шарового ротора.

Для

рас-

шифровки выходных сигналов датчиков^ углового положения

свободных гироскопов требуется специальное вычислительное

190

АЛГОРИТМЫ

ИНЕРЦИАЛЬНЫХ СИСТЕМ НАВИГАЦИИ

[ГЛ.

устройство. Алгоритм последнего, определяющий связь между дан-

ными сигналами

углами ориентации

i 7з

или

направляю-

щими косинусами

ащ

зависит

от

конкретной конструктивной

схемы свободного гироскопа.

5.5.

Пол у аналитическая инерциальная система

с непосредственным определением ориентации

опорного трехгранника

В заключение этой главы

мы

опять вернемся

системе полу

апалитического типа

азимутально-свободным опорным трехграж

ником, одна

из

осей которого ориентирована

по

гравитационной

вертикали,

т. е. с

опорным трехгранником

Метод построе-

ния алгоритма будет

некотором смысле гибридным. Подобно

тому,

как мы

делали'в

п.

5.4.1, будем определять ориентацию

трехгранника х1у'^

направляющими косинусами, которые будем

находить

из

решения линейных дифференциальных уравнений

(3.107).

Входящие

(3.107)

проекции абсолютной угловой скорости

(теперь

они

должны обозначаться через

ау,

») будут опре-

деляться

по

исходной информации, поставляемой акселерометра-

ми.

Такой подход

построению алгоритма обладает рядом осо-

бенностей. Соответствующий алгоритм будем строить

предпо-

ложении,

что

инерциальная система должна определять долготу

гравитационную широту ср"

как

первичные координаты. Гра-

витационную широту ф" легко преобразовывать

географическую

широту

ф по

формуле

(1.10).

Частично аналитические выражения искомого алгоритма

можно получить

из

общих соотношений, приведенных

в п. 5.2.5.

Функционирование акселерометра

идеальном случае описы-

вается уравнениями

(см.

(5.45))

t .,

=,.

а V - - а

(5.69)

где

У ", У

проекции абсолютной скорости

на

гравитационно-

го

"е „ „ „

горизонтальные

оси а£, yl

опорного трехгранника

Проекции

со % со «, to -

абсолютной угловой скорости трех-

"> х

. г

гранника

на его

собственные

оси

имеют

вид

, V - \

Ус

с 1

(5.70)

со

" = -

, V

со

» — —-„ ;

но

В В

5.5]

НЕПОСРЕДСТВЕННОЕ

ОПРЕДЕЛЕНИЕ ОРИЕНТАЦИИ

191

Первые

две

формулы

(5.70)

можно получить

из

(1.150)

или

(5.42)

при замене верхнего индекса

i на два

штриха

нижнего индекса

на

с,

причем фигурирующие

(5.83)

величины

i/R" , 1/R''

1/R

аналогичным образом могут быть получены

из

(5.31).

Они

имеют

вид

1 i ,» ,

a cos

ф"

cos

в"

a +

Ус

-}-

1 я

(1 + а

cos

ф" sin

^47£-асоа

cosXcSm'/

(5.71)

Ориентация опорного трехгранника

x'iylzl

относительно грави-

тационного трехгранника

x"y"z"

(ось у"

лежит

плоскости мери-

диана) определяется одним углом

(оси z" и z"

совпадают).

Это угол между осью

у" (х") и

осью

у'

(х'ё),

при > 0 ось у"

поворачивается

от оси у" в

сторону

оси х".

Ориентация гравита-

ционного трехгранника

x"y"z"

относительно абсолютного (инер-

циального) трехгранника £

Са

определяется двумя углами:

абсолютной долготой

гравитационной широтой ф". Матрицы

преобразования координатой системы

x"y"z"

коорди-

натной системы

x"y"z" в

Ъх-, которые

мы

будем обозначать

соответственно через

йг

», имеют

вид

С,

—

-— sin ---

sin

ср"

cos %

GOS ф* GoS

cos

— sin

ф"

sin X

cos

ф"

sin X-

0 cos

ф"

sin ф"

cos

sin X

-sinxc

cosXc

•

(5.72)

Матрица

может быть построена

по

таблице направляющих

косинусов

(1.76).

этой таблице нужно только вместо

£, п, £,

х,

у z, ф,

вписать соответственно

т}

, х", у", z\

ф",

Матрица

аС

суммарного преобразования,

т. е.

преобразования

координатной системы

получается

виде произ-

ведения матриц

аг

и С>

, т. е. в

виде

ас

аг

»С

»с-

Таким образом, получим

С,

г Mi)

'-ас

,031-.

'ас

23)

(33)

'ас

(5.73)

192

АЛГОРИТМЫ ИНЕРЦИАЛЬНЫХ СИСТЕМ НАВИГАЦИИ

[ГЛ. V

где

t-ac

Coo

-03)

(•ОС

-(2D

t-oc

„(22)

C-aC

t-ac

.(32)

—sin

Vcos Xc + sin ф* cos ^

sin Xo>

—sin k

sin Xc — sin Ф* cos X

cos %

COS ф" cos %

cos Xo cos Xc + sin Ф"

srn

sin Хо»

cos X

sin Xc — sin ф" sin %

cos Xct

cos ф" sin %

(

ас

]

—cos

ф" sin %c,

cos ф" cos xc, cSf

)

= sin ф".

Для вычислений

по

формулам

(5.71)

необходимы следующие выра-

жения, записанные

соответствии

с (5.73):

соэф"

sin Хс =

—<$а\

cos ф" cos Хс - CSJ • (5.74)

Для определения гравитационной широты

ф",

абсолютной дол-

готы

К и

угла ориентации

хё

опорного трехгранника

x'cy'cZc

в азимуте получим выражение

из (5.73):

8Шф" =

ас

„(23)

'«с

Д13)

tg Хс = -

,(зх)

ас.

(5.75)

Элементы

Сое

определяются

из

решений линейных дифферен-

циальных уравнений.

В соответствии

с (3.106) эту

систему уравнений можно записать

в виде опорного матричного уравнения

с-С

ас

-а

(5.76)

где

(5.77)

Матричное уравнение

(5.76)

содержит девять уравнений.

Мы

должны решить только шесть дифференциальных уравнений

(см.

п.

3.4.3). В

данном случае удобней решать уравнения, определяю-

щие элементы третьей строки матрицы

ас

, и,

например, второй

строки.

В обычной форме

эти

уравнения имеют

вид

0 0

„ -

—

со „

«с

— со

со

. 0

\ v

= -*

•(аз.

•

•'во I

"с

;'2З)

_ «о _

C-JC — "wic

"'32) _ (23)

Сас

— "С.

нс

5.5]

НЕПОСРЕДСТВЕННОЕ ОПРЕДЕЛЕНИЕ'] ОРИЕНТАЦИИ

193

,.(31) _ _

.(33) „(32) (38)

cff

= со -cgf* -

со

-cjp. п (5.78)

Элементы первой строки матрицы

ао

определяют направляю-

щие косинусы

оси |„ или

компоненты единичного 'вектора

§„.

Эти компоненты могут быть получены

из

векторного произведения

= 'Па X ta- В (5.75)

фигурирует только один элемент первой

строки

—

элемент

с^р.

Этот элемент определяется после решения

уравнений

(5.78) по

формуле

(18) _ (21) (32) (22) (31) /t-

т.

е.

элементы второй

третьей строк являются компонентами

единичных векторов

п" и £,1.

Информация

правых частях

(5.69)

поставляется акселеромет-

рами. После интегрирования

(5.69)

получаем

>•

и F,.» в

виде

функций времени, затем

по (5.70) и (5.71)

формируем

со - и со *.

В выражения

со - и to -

будут входить квадраты величии

"с

(31)

иСдс

, а

также

их

произведения,

так что

после подстановки

урав-

нения

(5.78)

развернутых выражений

для со - и со - они

стано-

Ус

вятся нелинейными. Нелинейные члены будут входить

уравне-

ния

(5.78) с

малым параметром

—

относительным коэффициентом

сжатия Земли

a = 3,35 -10~

После нахождения соответствующих

элементов

ас

координаты

, ср" и

азимутальный угол опорного

трехгранника

хё

определяются тригонометрическими формулами

(5.75).

В данном варианте алгоритма вычислительные формулы

не

содержат величин, обращающихся

бесконечность

на

полюсах

Землп

*).

Вычисление

, Хс

можно производить

любой близости

от

полюсов.

На

полюсах вторая

третья формулы становятся

не-

определенными.

Мы

можем

Ха и Хс

доопределить предельными

значениями, зависящими

от

траекторий подхода

полюсам.

Интересно отметить,

что

если

алгоритме можно воспользо-

ваться сферической моделью Земли

принять

Я" — R" = R =

—

+ h и R

= 0, то

уравнения

(5.91)

будут линейными.

} Читателю предлагается сравнить

формулами счисления

7 П. и.

Бромберг

Г Л ABA VI

УРАВНЕНИЯ ОШИБОК

§ 6.1. Система с ориентацией опорного трехгранника

но географической вертикали

6.1.1. Общие положения. В предыдущей главе были рассмот-

рены алгоритмы инерциальных систем навигации. Алгоритмы

не могут быть точно воспроизведены в инерциальных навига-

ционных системах. При их реализации возникает ошибка, обус-

ловленная неизбежными несовершенствами отдельных элементов.

Вследствие этого координаты местоположения объекта и компо-

ненты скорости движения, получаемые на выходе инерциальной

системы, которые мы будем называть приборными или расчет-

ными значениями соответствующих величин, будут несколько

отличаться от своих действительных значений.

Эти отклонения или выходные ошибки инерциальных систем

зависят от различных причин. Эти причины будут являться вход-

ными возмущениями или входными ошибками инерциальных

систем. Входные возмущения будем разбивать на четыре класса:

на методические и инструментальные ошибки, ошибки в установке

осей чувствительности измерительных элементов и ошибки на-

чальной выставки инерциальных систем.

Методические ошибки обуславливаются ошибками алгоритма,

положепного в основу функционирования системы. Ошибки алго-

ритма могут зависеть от неполноты наших знаний о соответству-

ющих физических явлениях. В данном случае это прежде всего

относится к структуре и количественным характеристикам гра-

витационного поля Земли, к величине и направлению угловой

скорости ее суточного вращения и к параметрам, определяющим

фигуру Земли. В некоторых случаях методические ошибки как бы

заранее планируются в процессе проектирования системы. Так

поступают тогда, когда методические ошибки, возникающие при

упрощении алгоритма, компенсируются улучшением других ха-

рактеристик инерциальной системы: уменьшением инструменталь-

ных ошибок, повышением надежности системы, упрощением работы

с ней в процессе эксплуатации, повышением экономичпостн.

Под инструментальными ошибками мы понимаем ошибки чув-

ствительных элементов системы и ошибки вычислительного уст-

g 6.1] ОРИЕНТАЦИЯ ПО ГЕОГРАФИЧЕСКОЙ ВЕРТИКАЛИ Ю5

ройства. Это прежде всего собственный дрейф гироскопов и

смещение нуля акселерометров — приборов, являющихся измери-

тельными элементами системы, а также дрейф нуля интегриру-

ющих элементов вычислительного устройства. Кроме того, такого

рода ошибки могут быть обусловлены отклонением безразмерных

масштабных коэффициентов от своих номинальных значений,

равных единице.

Следующая группа ошибок является специфичной для инер-

циальных систем, такие ошибки в зарубежной литературе иногда

называют ошибками конструкции. Их возникновение можно пояс-

нить следующим образом. Рассмотренные раньше алгоритмы были

построены в предположении {хотя это и не является принципи-

альным), что соответствующие измерительные оси акселерометров

и оси чувствительности гироскопов параллельны. В реальных кон-

струкциях указанные оси могут оказаться рассогласованными па

небольшие углы из-за неизбежных погрешностей в установке из-

мерительных приборов относительно базовых площадок. Этот

факт вызывает дополнительные ошибки на выходе инерциальных

систем. Анализ ошибок конструкции позволяет вырабатывать обос-

нованные требования к технологии выставки осей измерительных

приборов относительпо тем или иным способом материализован-

ных осей опорного трехгранника.

И паконец, к последней группе ошибок, и также специфичных

для инерциальных систем, относятся ошибки начальной выставки.

Они обуславливаются следующими причинами. К моменту

запуска инерциальной системы необходимо на выходах всех инте-

грирующих элементов установить начальное значение соответст-

вующих величин (координат местоположения объекта, проекций

скорости движения, угла отклонения в азимуте платформы от

направления соответствующего меридиана и т. д.). Здесь ошибки

могут возникать из-за неточной внешней информации об этих

величинах к моменту запуска системы, а также из-за инструмен-

тальных погрешностей устройств ввода начальных значений в ин-

тегрирующие элементы системы. Кроме того, ошибки могут воз-

никать из-за того, что мы не можем точно определить ориентацию

моделирующего (приборного) опорного трехгранника относитель-

но действительного опорного трехгранника. Ошибки начальной

выставки порождают собственные колебания инерциальной систе-

мы.

Для неустойчивых систем ошибки, порожденные неточной

начальной выставкой, будут возрастать с течением времени, для

асимптотически устойчивых систем они, наоборот, с течением вре-

мени будут стремиться к нулю. В промежуточном случае, когда

система будет удовлетворять условиям обыкновенной устойчи-

вости, эти ошибки будут иметь колебательный характер или стре-

миться к некоторой постояиной величине. Параметры колебатель-

ного движения и указанная выше постоянная величина зависят