Brewster H.D. Mathematical Physics
Подождите немного. Документ загружается.


42
Mathematical
Basics
logarithmic order at x
~
00,
then we say that the integral F
(E)
has a weak
singularity.
Power Singularity on a Bounded Interval
Let a,
a,
~
ERa,
~
> 0, be some real numbers and E > ° be a small
positive prameter. Let
<p
E
Coo
[0, a] be a smooth function on [0, a]. We will
study the asymptotics as
E
~
0+
of
the integrals
of
the form
F(E)=
f
t13
-
1
(t+E)u<p(t)dt.
Remarks. The function F
is
holomorphic
in
complex plane E with a cut
along the negative half-axis. At the point
E = ° this function has a singularity
(if
a>
0
is
not integer).
The type
of
this singularity
is
determined by the behaviour
of
the function
<p
at small t::;
0.
Standard Integral. One needs the following result. Let a and
~
be two
complex numbers such that Re
~
> 0 Re a < 0 and Re
(~
+
a)
<
0.
Then
[
t
13
-
1
(t
+
l)u
dt = rc(3)rc
-a
-(3),
(0 < Re
13
< -
Rea)
rc-a)
.
Theorem: Let
<p
E
C""[O,
a]. Let
r,
8>
° and
S8
=
{E
E
ClO
<
IE}
::;
r,
larg
EI
::;
1t -
8}
be a sector
in
the complex plane
of
E.
1.
If
a +
13
is
not integer, then
~
f(l3+n)f(-a-l3-n)<p(n)(O)
u+l3+n
~
11
F (£) -
f::o
f(
-a)
E +
f::o
ailE
(E~O,
EES/).
2.
If
a +
13
= N is an integer, then
~
f(N
+ n)
<p(Il)
(0)
n+N
1 ~ b
11
F ( E) -
L..J
,E
n E +
L..J
IlE
ll~max{O._N)f(a)f(N+n-a)
n.
11=0
(E~O,
EESIJ.
The coefficients
all
and b
ll
depend on the values
<pet)
for 0
::;
t
::;
a. The
branch
for
the
functions
E
and
In
E is
choosen
in
such
a
way
that
£1>
° and
In
E
is
real for
E>
O.
Examples: In all examples
<p
E
C""([O,
aD
is
a smooth function bounded
with all its derivatives.
1.
Let ° < a < 1 and
Then
F(E)
= f
<pet)
dt
.
.b
t
+
E

Mathematical
Basics
F(E)=-cp(O)lnE+O(l),
(E-+O+)
2.
Let 0 < a < 1 and
f
cp(t)
.
F (£) =
.b
2 2 dt
t +E
By using
1 =
_I
(_1
___
1_1
t
2
+E2
2iclt-ic
t+ic)
we obtain from the previous example
3. Let
a >
112
and
Then
(0).J;r(a-1I2)
\-2a
0(3-2a)
0(1)
(c-+O+)
F (£) =
cp
2
rea)
E + E + ,
POWER SINGULARITY
ON
UNBOUNDED
INTERVAL
Standard Integral
43
To compute the following asymptotics one needs the following standard
integral.
Let Re
~
> 0 and Re a > -
1.
Then
roo
a
-ti3d
_ 1
r(a+l)
.b
t e t -
13
-p-,
(Re(3
>
0,
Rea>
-1).
Examples: Let
q>
E C'" ([a,
00))
be
a smooth function on
[a,
00)
that has
asymptotic expansion as x
-+
00.
1.
Let
a,
~
>
0,
and
F(c)
= r
cp(x)xue-e.xPdx
If
a <
-1,
then the integral
is
not singular as £
-+
0+.
Its asymptotic
expansion can be obtained either by integration by parts or by a change

44
Mathematical
Basics
of
variables. So, let now a + 1 > 0 and let
N=
[a
+
1]
£:
~
0+
be the
integer part
of
a +
1.
Let us single out the first N + 1 terms
of
the
asymptotic expansion in
<p,
i.e.
N
<p(x)
= L
ak
x
-
k
+ RN(x)
k=O
Since R,\{x) = O(x-
(N
+1»
as x
~
00,
we have
N
" r
a-k
-EX
J3
d
F(e)=L..ak
x e
x+O(l).
k=O
Now by changing the variables and extending the interval to [0,
00)
we obtain
a-k+l[
1
N a
---
a-k+l
F (e) = L -.l..e
~
r(
) + 0(1) + 0(1)
k=O
P P
If
a = - I, then
2.
Let a > 0 and let
p (x) =
xn
+
...
+
a1x
n
~
l.
Consider the integral
F (e) = r
<p(x)xae-EP(x)
dx.
If
a > - I, then the main term
of
the asymptotics
is
F(e)=
~r(
a:lr:+
1
+o(e-*)'
(£->0+)
Ifa
= - I then
F(e)=
-~lne+O(1),
(e-+O+)
If
a < I, then the integral
is
not singular as e
~
0+.
By integration by
parts the integral can be reduced to the cases considered above.

Chapter 2
Laplace and Saddle Point Method
LAPLACE
INTEGRALS
IN
ONE
DIMENSION
Let
M=
[a,
b]
be a closed bounded interval,
S:
M
-7JR
be a real valued
function,
<p:
M
-7
C a complex valued function and A be a large positive
parameter. Consider the integrals
of
the form
F (A) = r <p(x)exp[AS(x)]dx.
Such integrals are called Laplace integrals. We will study the asymptotics
of
the Laplace integrals as A
-7
00.
Lemma: Let sUPa<x<b
Sex)
= L <
00
and the integral converges absolutely
for some
AO
>
o.
Then
1.
IF(A)I
~
CleALI
(Re
A
~
AO).
2.
If
J,
S E C(a, b),
then
F(A)
is
holomorphic
in
the
halfplane
Re
A>
AO.
Watson
Lemma
Lemma: (Watson) Let 0 < a <
00,
ex> 0,
~
> 0 and let
Sf.
be the sector
Sf.
=
{A
E ell arg
AI
~
1t/2
e}
in the complex plane
A.
Let
<p
E
COO([O,
aD
and let
cI>(A)
=
.b
<p(x)x~-l
exp(-Axu)dx
Then, there is an asymptotic expansion as A
-7
00,
A E
Sf.'
-.!..
~
A-(~+k)/ur([3+kJ
<p(k)
(0)
cI>
(A)
- a
f:o
a k!
Laplace
Transform
Let
<p
E
COO(JR+)
be a smooth function on the positive real axis such that
its Laplace transform
C(<p)(A)
= r
<p(x)e-Axdx
converges absolutely for some
AO.
Then

46
Laplace and Saddle Point Method
00
C(cp)(A.)
- I
A.
-kcp(k)
(0)
(IAI
~
00, A E Sf:)
k=O
Interior Nondegenerate Maximum Point
Let now
Sand
cp
be smooth functions and the function S have a maximum
at an interior point
Xo
of
the interval
[a,
b], i.e. a <
Xo
<
b.
Then
S/(xo)
=
O.
Assume, for simplicity, that S"(x
o
) <
O.
Then
S"
(x
o
)
<
O.
In other words, in a neighborhood
of
Xo
the function S has the following Taylor
expansion
2
Sex)
=S(xo)+S"(xo)
(x-xo)
+O«x-xO)3).
2
Such a point is called nondegenerate critical point. Then, as
A.
~
00
the
main contribution to the integral comes from a small neighborhood
of
xO.
In this neighborhood the function
<p
is almost constant and can be replaced
by its value at
xO.
The terms
of
order (x - x
O
)3
can be neglected in the exponent
and the remaining integral can be extended to the whole real line. By using
the standard Gaussian integral
roo
ex
p
( -
~
y2
)dy
==
fl.,
(Re
(l
>
0),
one obtains finally the main term
of
the asymptotics
'I
A -112
~<p(x
)eA.S(x
o
)
F(II.)-
V~
0
One can prove the general theorem.
Theorem: Let M =
[a,
b]
and
cp,
S E
CO
(M), S has a maximum only at
one point x
o
' a
<
Xo
<
band
S"(x
o
)
*
O.
Then as
A.
~
00,
A E
SE
there is
asymptotic expansion
00
F
(A.)
-
eA.S(xo)
I
Ck
A
-1I2-k
.
k=O
The coefficients c
k
are expressed in terms
of
derivatives
of
<p
and S at
xO.
The theorem can be proved as follows. First, we change the integration variable
x =
Xo
+ A
-ll2y.
So, y is the scaled fluctuation from the maximum point
xO.
The interval
of
integration should be changed accordingly, so that the maximum point is
now
y
==
O.
Then, we expand both functions
Sand
<p
in
Taylor series at
Xo
getting

Laplace
and
Saddle
Point Method
47
'I
"(
) 1
SW(
) 2
~
S(n)(XO)
n'l
-(n-2)/2
lnS(X
+
1..-
1I2
y)
=
fY:)
Xo
+ -
Xo
Y +
L..J
,Y
I\.
'Y
0 2
n=3
n.
~
<p(n)(xo)
n'l
-n/2
q>(x
+
1..-
1/2
y)
=
L..J
,y
I\.
o
n=O
n.
Since the quadratic terms are
of
order
0(1)
we
leave it in the exponent
and expand the exponent
of
the rest in a power series. Next, we extend the
integration interval to the whole real line and compute the standard Gaussian
integrals
of
the form
.c
ex
p
( -
~
l
)lk+ld
Y
= 0,
.c
ex
p
( -
~
l
)lkd
Y
=r(k+~)(~rk-l,
where k is a nonnegative integer and a has a positive real part, Re a > 0.
Finally,
we
get a power series in inverse powers
of
A..
The coefficients
ck
of
the asymptotic expansion are polynomials in the higher derivatives S (k)(x
o
), k
~
3, and derivatives
<p<D(xo)'
I
~
0, and involve inverse powers
of
SIt
(x
o
).
Stirling Formula
r(x
+ 1) =
~xx+1/2e-X[1
+
O(x-
1
)],
(x
~
00)
is obtained by applying the Laplace method to the integral
r(x
+ 1) = xx+l r exp[x(lnt
-t)]dt
Stieltjes
Transform
Let
<p:
lR+
4 C have finite moments
mn(<p)
= r tn<p(t)dt <
00
Then the Stieltjes transform
of
<p
S(q»(x) = F
<p(t)
dt
.b
t+x
has asymptotic expansion as x 4
00
00
S(q»(.t) _ L (_1)k
mk(<p)x-
1
-
k
k=O
Boundary
Maximum
Point
Let the function S have a maximum at a boundary point
Xo
=
a.
Let, for

48 Laplace and Saddle Point Method
simplicity,
S'
(a)
~
0, i.e.
S'
(a) < 0, and
<pea)
~
O.
Then, as A
~
00,
the main
contribution to the integral comes from the interval
[a, a +
E],
where
Sex)
= S (a) + (x - a) S'(a) +
O(x
-
a)2).
Now, by replacing the function
<p
by its value at a and neglecting nonlinear
terms in
Sex),
we get
F
(A)
_A-I'
_~(,~~)
e'AS(a)
,
(A
~
00)
In this way one can prove the following theorem.
Theorem: Let
M=
[a,
b],
<p,
S E CO(M), S has a maximum only
at
the
point
x = a and S'(a)
~
O.
Then, as A
~
00,
A E
Sf.'
there is asymptotic expansion
a.
00
F
(A)
_e'AS(a)
L
ck
A
-I-k.
k=O
The coefficients C k are expressed in terms
of
derivatives
of
cp
and S
at
x =
Error Function: The asymptotic expansion
of
the (complementary) error
function as
x
~
00
has the form
~
rx
a-I
-td
Enc
X =
.b
t e
t,
(0 < a <
00,
x > 0)
Incomplete Gamma Function: The incomplete gamma-function
( )
r
a-I
-td
y
a,x
=.b t e
t,
(0 < a <
00,
x>
0)
has the following asympotic expansion as x
~
00
(
)
=
r(a)+e-xxa-I
~
rea)
x-
k
ya,x
(;orc
a
-
k
)
BACKGROUND
FROM
ANALYSIS
1.
Let
xi,
j =
1,
... , n
be
real
numbers
and let
x
be
the
n-tuple
x = (xl, ... x"). The set
of
all n-tuples
of
real numbers is denoted by
Rn.
A connected open subset n
of
]Rn
is called a domain. The set
an
of
boundary points
of
n is called the boundary
of
n.
The union
[n
u
an
is called the closure
of
and is denoted by
n.
2. Let
x,
X E
]Rn.
Then the scalar product
of
x and
~
is defined by
X·
~
=
xl~1
+
...
+
x"~n.
3. On]Rn there is standard Lebesgue measure dx = dx
l
...
dx
n
.
4. Let
0J,j
=
1,
... ,
n,
be non-negative integers, a
J
~
O.
The n-tupl a =
(a
l
, ... ,
an) is called a multi-index. Further, let
lal = a
l
+
...
+
an
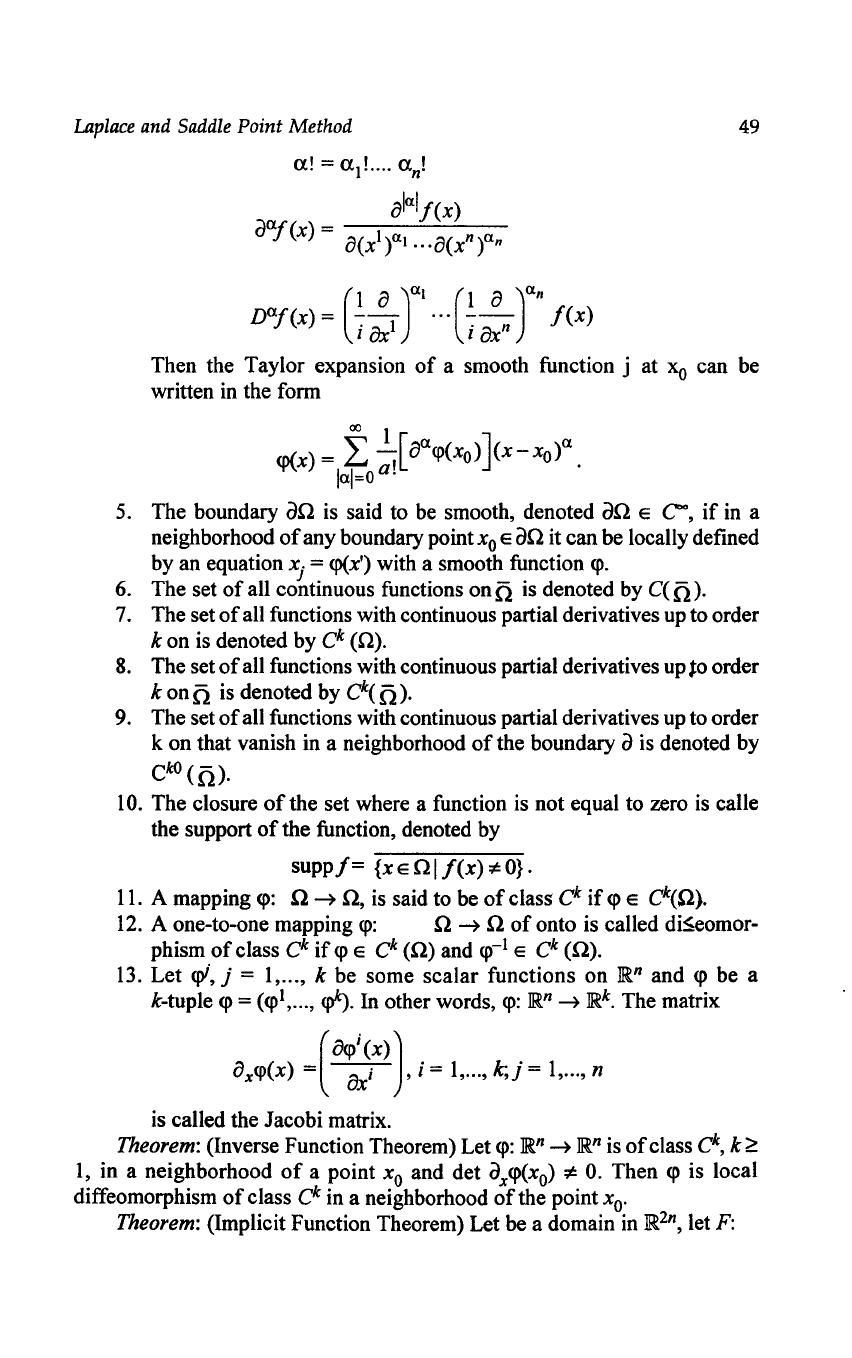
Laplace
and
Saddle
Point Method
49
a!
=
aIL.
..
an!
(
1
8
)a
1
(
1 8
Jan
Daf(x)
=
-:-
...
-:-
f(x)
I
ax
I
18xn
Then the Taylor expansion
of
a smooth function j at
xo
can be
written in the form
<p(x)
= I
~[aa<p(Xo)]<x_xo)a.
lal=oa.
5.
The boundary
aQ
is said to be smooth, denoted
aQ
E C"',
if
in a
neighborhood
of
any boundary point
Xo
E
aQ
it can be locally defined
by an equation
Xj
=
<p(x')
with a smooth function
<po
6. The set
of
all continuous functions on 0 is denoted by C( 0).
7.
The set
of
all functions with continuous partial derivatives up to order
k on is denoted by C
k
(0).
8.
The set
of
all functions with continuous partial derivatives up
fO
order
k on 0 is denoted by C
k
(
0).
9.
The set
of
all functions with continuous partial derivatives up to order
k on that vanish in a neighborhood
of
the boundary a is denoted by
C
kO
(0).
10.
The closure
of
the set where a function is not equal to zero is calle
the support
of
the function, denoted by
suppf=
{XE
01
f(x);t:
O}.
11.
A mapping
cp:
Q
~
Q,
is said to be
of
class C
k
if
cp
E
Ck(Q).
12.
A one-to-one mapping
cp:
Q
~
Q
of
onto is called
di~eomor-
phism
of
class C
k
if
cp
E C
k
(0)
and
q>I
E C
k
(Q).
13.
Let
cpi,
j =
1,
... , k be some scalar functions on
~n
and
cp
be a
k-tuple
cp
=
(cpI
,
...
,
cpk).
In other words,
cp:
]Rn
~
]Rk.
The matrix
axcp(x)
~(
~x»).;
~
I
•...•
k;j
~
I
•...•
n
is called the Jacobi matrix.
Theorem:
(Inverse Function Theorem) Let
cp:
]Rn
~
~n
is
of
class C
k
, k
~
1,
in a neighborhood
of
a point
Xo
and det
ax<p(x
o
)
;t:
O.
Then
cp
is local
diffeomorphism
of
class C
k
in a neighborhood
of
the point
xO.
Theorem:
(Implicit Function Theorem) Let be a domain in
]R2n,
let
F:

50 Laplace and Saddle Point Method
F: 0
~
lR
n
be
a
mapping
of
class CkO)
and
let (xo,
Yo)
E 0
be
a
poin
in
o such
that
F (xo'
Yo)
= 0, det
8),.F
(xo,
Yo)
*-
o.
Then
in a
neighborhood
of
the
point
Xo
there
is a
mappingy
=
f(x)
of
class C
k
such
that
Yo
=
f(xo)
and
F
(x,j
(x»
==
o.
Morse Lemma
Let
S: 0
~
lR
be
a real valued
function
of
class C
k
on
a
domain
0
in
lR
n
with k
~
2.
Let
Definition:
1.
The
point
Xo
is
called a critical point
of
the function S
if
8S(xo)
= 0
2.
A critical
point
Xo
is
called non-degenerate
if
det
a.~S
(xo)
*-
O.
3.
The
determinant det
~S
(x
o
)
is
called the Hessian
ofthe
function
Sat
the point
xo'
Lemma: (Morse) Let S:
lR
n
~
Rand
Xo
ElR
n
be
a non-degenerate critical
point
of
the function S.
Let
SE
ex'
in
a neighborhood
of
the
point
Xo
and
let
'!.i
*-
O,}
= I,
...
, n
be
the eigenvalues
ofthe
matrix
~S
(xO>.
Then
there are neighoorhoods U
and
V
of
the
points
Xo
and
0
and
a
smooth
local diffeomorphism
cp:
V
~
U
of
class ex' such
that
det 8
y
cp(0)
= 1
and
1
~
·2
S(cp(y»
=S(xO>+2~J.l/Y).
)=1
Remark: Nondegenerate critical points are isolated.
Gaussian
Integrals
Proposition:
Let
A =
(aij
be
a complex symmetric nondegenerate n X n
matrix with the eigenvalues
J.l.
(A),)
= I, ... ,
n,.
Let
Re
A
~
0, which means
that
X·
Re
A x
~
0
'v'XElR
n
,
x
*-
O,J
or
Re
J.lj
(A)
~
O,}
=
1,
... ,
n.
Then
for').. >
0,
; E
lR
n
there holds
k
nexp
(
-
~
X.AX-i;.X)dx
=
(~r/2
(detA)-1I2
exp
( -
2~
;.A-
1
;)
The
branch
of
.JdetA
is
choosen as follows
(det A)-1I2 = IdetAr1l2 exp(
-i
Ind
A),
where

)""
Laplace
and
Saddle
Point Method
51
1 1
IndA
= -
Largll}
(A),
largll}(A)I::;~2
2
'-1
By
expanding
both
siCi~s
of
this
equation
in
Taylor
series in
::;
we
obtain
the
following result.
Corollary:
k
n
exp( -
~
X·
Ax ) xii ...
xi2k+1dx
= 0
k
n
exp ( -
~
x . Ax ) xii ...
xi2k
dx
=
(
21t)nI2 (detA)1I2(21-)-k
(2k)!
G0Ji2
...
GI2k-li2k)
I-
k!
Here k
is
a non-negative integer, G =
A-I,
and
the
round
brackets
denote complete symmetrization over all indices included.
An
important
particular case
of
the previous formula
is
when the
matrix A
is
real.
Proposition: Let A
be
a real symmetric nondegenerate n X n matrix. Let
v +(A)
and
v _
(A)
be
the
numbers
of
positive
and
negative eigenvalues
of
A
and
sgnA
= v+
-v_
be
the
signature
of
the
matrix
A.
Then
for
I-
> 0,
~
EIRn
there holds
k
n
exp(i~
x·Ax-i~·x
)dx
1t
112
1
-1
l1t
(2
)
n12
(.
. )
= T IdetAI -
21-
~·A
+4
sgn
(A)
LAPLACE
INTEGRALS
IN
MANY
DIMENSIONS
Interior
Maximum
Point
Let
be
a
bounded
domain in
IRn,
S:
~
IR,f
n
~
<C
are
some functions
on
n
and
I-
> 0
be
a large positive parameter.
We
will study
the
asymptotics
as
I-
~
00
of
the
multidimensional Laplace integrals
F
(::;)
=
bf(x)exp[AS(x)]dx.
Let S
andfbe
smooth functions and the function S have a maximum only
at
one
interior
nondegenerate
critical
point
Xo
E
n.
Then
8
x
S (x
o
) = 0
and
[det a.;S(x
o
)]
<
O.
Then
in a
neigbborhood
of
Xo
the
function S
has
the
following
Taylor
expansion
