Brewster H.D. Mathematical Physics
Подождите немного. Документ загружается.


272
Special
Functions
2 2
=
X2
_ < x
,1
> 1 _ < x , x > x
111112
II
X
l1
2
2
=X
--
3·
Table: Common classical orthogonal polynomials with
the interval and weight function
used to define them
Polynomial Symbol Interval
cr(x)
Hermite
Hn(x)
(-00,00)
e-
x2
Laguerre
L~(x)
[0,
00)
e-
X
Legendre
Pn(x)
(-I,
I)
I
Gegenbauer
C~
(x)
(-I,
I)
(1-
x2)i..-1/2
Tchebychef
of
the
1st
kind
Tn(x)
(-I,
I)
(1-
x
2
)-1/2
Tchebychef
of
the 2nd kind
Un(x)
(-I,
I)
(1-
x2)-1/2
Jacobi
p~V'Il)
(x)
(-I,
I)
(I
- xlv
(1-
x)1!
So far, we have the orthogonal set
{1,X,X
2
-~}
.
If
one chooses
to
normalize these by forcing
<Pn(l)
=
1,
then one obtains the classical Legendre
polynomials,
Pn(x) =
<Pn(x).
This
is
not the typical normalization. Also, it might
not be clear where the normalization constant
is.
The
<Pn's
can be multiplied by any constant
and
this will only affect
the
"length",
lI<p
n
lf. Thus,
we
have so far
that
<pz<x)
=
C(
x
2
-
~).
Setting
x =
1,
<P2
(1) =
3..
Therefore, one obtains
3
1 2
Pz<x)=<P2(x)=2"(3x
-1).
The set
of
Legendre polynomials isjust one set
of
classical orthogonal
polynomials
that
can be
obtained
in this way.
Many
had
originally
appeared as solutions
of
important boundary value problems in physics.

Special
Functions
273
II
0
I
2
3
Table: Tabular Computation
of
the Legendre
Polynomials
Using the Rodrigues Formula
n
1
d 2 n
(.\
2
-
on
-(x
-1)
-
dx
n
2
n
I
n.
1
I I
X2
_ I
1
2x
-
2
1
x4
-
2x2
+ I
12x2
- 4
-
8
x6
-
30
+
3x
2
+ I
12x2
- 4
120x
3
-72x
Pn(X)
I
x
1
- (3x
2
-
1)
2
1
-(5x
3
-
3x)
2
LEGENDRE POLYNOMIALS
In the last section we saw the Legendre polynomials in
the
context
of
orthogonal bases for a set
of
square integrable functions in
L2
(-1,
1).
In your
first course in differential equations, you saw these polynomials as one
ofthe
solutions
of
the differential equation
(1
- x
2
)y"-2xy'
+ n(n +
l)y
= 0, n E N.
Recall
that
these were
obtained
by
using
power
series
expansion
methods.
A few
of
the properties
of
these functions. First, there
is
the
Rodrigues
formula.
1 d
n
2 n
P
(x)
=--(x
-1)
, n E N.
n 2nn!dxn
From
this,
one
can
see
that
Pn(x)
is
an
nth
degree polynomial. Also,
for
n
odd,
the polynomial
is
an
odd
function
and
for n even,
the
polynomial
is
an
even function.
One can systematically generate the Legendre polynomials in tabular form.
Note
that
we get
the
same result as we
found
in
the
last section using
orthogonalization.
The
classical orthogonal polynomials also satisfy three term recursion
formulae. In the case
of
the Legendre polynomials, we have
(2n
+
l)xP
n
(x)
=
(n
+
I)P
n
+
l
(x)
+ nPn_l(x), n =
1,2,
....
This
can
also be rewritten by replacing n with n - 1 as
(2n -
l)xP
n
_
l
(x)
= nPn(x) +
(n
-
I)P
n
_
2
(x), n =
1,2,
....
We will prove this two different ways.
First, we use the
orthogonality
properties
of
Legendre polynomials
1 (2n)!
and
the fact
that
the coefficients
of
xn
in P (x)
is
-n--,-'
This last fact
n 2 n! n.
can
be
obtained
from Rodrigues formula. We see this by focussing
on
the
274
Special
Functions
leading coefficients
of
(x2
- 1
)n,
which is
x2n.
The first derivative is
2nx2n-
l
. The second derivative
is
2n(2n - 1
>.x2n-2.
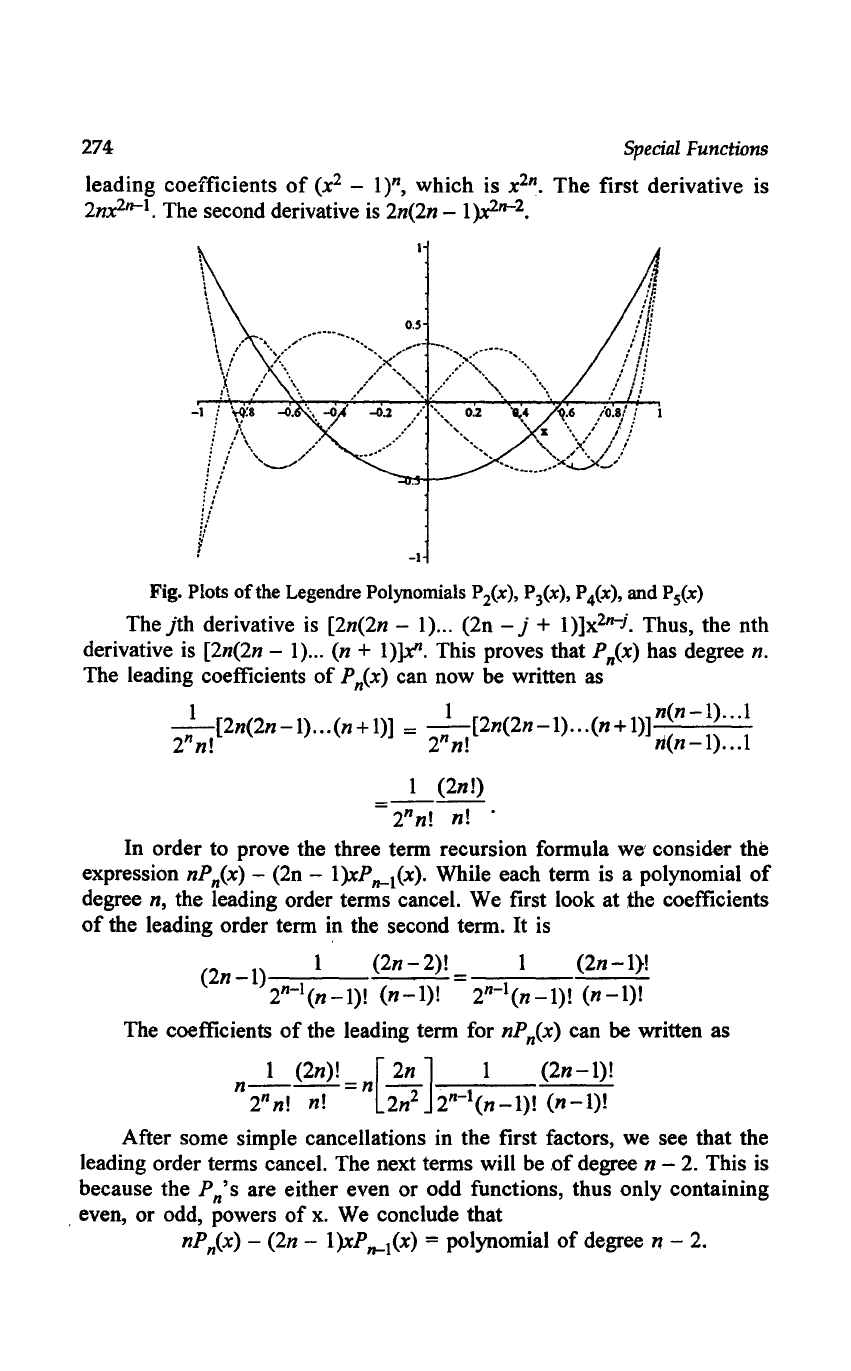
Fig. Plots
ofthe
Legendre Polynomials P
2
(x), P
3
(x), P
4
(x), and Ps(x)
The
jth
derivative is [2n(2n -
I)
... (2n - j +
1)]x2n-j.
Thus, the nth
derivative
is
[2n(2n -
I)
... (n +
I)~.
This proves that Pn(x) has degree
n.
The leading coefficients
of
P n(x) can now be written as
1 1 [2 (2 I) (
I)]n(n-l)
..
.l
-[2n(2n-I)
...
(n+I)]
= - n
n-
...
n+
2nn! 2nn!
n(n-I)
..
.l
1
(2n!)
-----
2nn!
n!
.
In order to prove the three term recursion formula
we'
consider the
expression nPn(x) - (2n -
I)xP
n-l(x). While each term is a polynomial
of
degree
n,
the leading order terms cancel. We first look at the coefficients
of
the leading order term
in
the second term. It is
(2n
-I)
1 (2n -
2)!
2
n
-
l
(n_I)!
(n-l)!
1
(2n-I)!
2
n
-
l
(n
-I)!
(n
-I)!
The coefficients
of
the leading term for nPn(x) can be written as
1 (2n)!
[2n]
1
(2n-l)!
n
2nn
!--;;t=n
2n2
2
n
-
1
(n_I)!
(n-l)!
After some simple cancellations in the first factors, we see that the
leading order terms cancel. The next terms will be
of
degree n - 2. This is
because the
Pn's are either even or odd functions, thus only containing
, even, or odd, powers
of
x.
We
conclude that
nPn(x) - (2n -
I)xP
n-l(x)
= polynomial
of
degree n - 2.

Special
Functions 275
Therefore, since the Legendre polynomials form a basis,
we
can write
this polynomial as a linear combination
of
of
Legendre polynomials.
nPn(x) - (2n - I)xPn_l(x) = cc/'o(x) + cIP1(x) +
...
+
cn-2
P
n-2(x).
Multiplying by P
m(x)
for m = 0,
1,
... , n - 3, and integrating from
-1
to
1,
we obtain
0=
cmllP
mll
2
using orthogonality. Thus, all
of
the~e
cm's are zero,
le~ving
nPn(x) - (2n - l)xP n-I(x) =
cn-2
P
n-2(x).
The
_
final
coefficients
can
be
found
by
using
the
normalization
condition, Pn(l) =
1.
Thus,
cn-2
= n - (2n -
I)
=
-(n
-
1):
A second
proof
of
the three term recursion formula can be obtained
from the generating function
of
the Legendre polynomials. Many special
functions
have
such
generating functions.
For
Legendre polynomials
the
generating function
isgiven
by
1
g(x, t) =
i~i=I_=2=x=t
+=t=2
co
L Pn(x)t
n
,
Ixl
<
I,
It
I <
1.
n=O
Fig. The Position Vectors
used-
to Describe the Tidal
force on the
Earth
Due
to the Moon
This generating function occurs often in applications. In particular, it arises
in potential theory, such as electromagnetic
or
gravitational potentials. These
1
potential functions are
;:
type functions.
For
example,
the
gravitational
potential between the Earth and the moon
is
proportional to the reciprocal
of
the magnitude
of
the difference between their positions relative to
some
coordinate system.
An even better example, would be to place the origin at the centre
of
the Earth
and
consider
the forces
on
the
non-pointlike
Earth
due
to
the
moon. Consider a piece
of
the Earth at position r 1 and the moon
at
position
r
2
•
The tidal potential $ is given as
$cx:: 1 1 1
Ir2
- Ii I
~(r2
-
Ii)'
(r2
-
Ii)
~li2
-
2rlr2
cose
+ r{

276 Special Functions
where
~
is
the angle
between'l
and
'2'
Typically, one
of
the position vectors
is
larger
than
the other.
In
this case,
we
have
'I
«
'2'
So, one can write
<Doc
1
=1
1
~r?
-
2rlr2
cosS +
ri
r2
'i
[rl
)2
1-2-cosS+
-
r2
r2
Now, define x = cos
Sand
t = !L . We then have the tidal potential
is
r2
proportional to the generating function for the Legendre polynomials! So,
we
can write the tidal potential as
<Doc- L P
n
cos(S)
!L
1
co
[
)n
r2
n=O
r2
The first term in the expansion will give the usual force between the
Earth
and
the moon as point masses,
or
spheres. The next terms will give
expressions for the tidal effects.
Now
that
we
have some idea
as
to where this generating function might
have originated, we now make some use
of
it. First
of
all, it can be used
to
provide values
of
the Legendre polynomials at key points. Thus, P
n(O)
is
found
by looking
at
g(O,
t),
1
co
n
g(O,
t) = M =
LPn(O)t
.
l+t
n=O
However, we can use the binomial expansion
to
find
our
result.
Namely, we have
1 1 2 3 4
~1+t2
=1-"2
t
+8
t
+ ...
Comparing these expansions,
we
have the Pn(q) = 0 for n
odd
and
n
(2n-l)!!
one can P
2n
(O)
= (-1) (2n)!! for n even. [note
that
the double factorial
is
defined by
n!!
=
(n
- 2)(n - 2)!!' So,
5!!
= 5(3)(1)
and
6!!
= 6(4)(2).]
A simpler evaluation
is
to find
Pi-I).
In
this case we have
1 1 2 3
g(-l,
t) = = 1+1 =
I-t+t
-t
+ ...
~1+2t+P
Therefore,
Pi-I)
=
(-I)n.

Special Functions 277
We can also use the generating function to find recursion relations.
To prove the three term recursion that
we
introduced above,
we
need only
differentiate the generating function with respect to t in equation and
rearrange the result. First note that
ag
x-t
x-t
- = =
g(x
t)
at
(1-
2xt
+ t
2
)3 /
2
1 -
2xt
+ t
2
,.
Combining this with
00
ag
= L
nPn(x)t
n
-
1
at
n=O
'
we
have
00
(x
-
t)g(x,
t)
=
(1-
2xt
+ t
2
)
L
nPn(x)t
n
-
1
•
n=O
Inserting the series expression for
g(x,
t)
and
distributing the sum
on
the right
si~e,
we
obtain
00 00 00 00
(x-t)LnPn(x)t
n
=
LnPn(x)t
n
-
1
_L2nxP
n
(x)t
n
+
LnPn(x)t
n
+
1
n=O n=O n=O n=O
Rearranging leads to three separate sums:
00 00 00
LnPn(x)t
n
-
l
-
L(2n+l)xP
n
(x)t
n
+
L(n+l)P
n
(x)t
n
+
1
=
o.
n=O
n=O
n=O
Each term contains powers
of
t that
we
would like to combine into a
single sum. This
is
done by reindexing.
For
the first sum,
we
could use the
new index
k = n -
1.
Then,
00 00
L
nPn(x)t
n
-
1
= L
(k+
1)P
k
+
1
(X)t
k
•
n=O
k=-l
These different indices are
just
another way
of
writing out the terms.
Note that
00
""
nPn(x)t
n
-
1
2
LJ
= 0 +
lj(x)
+
2P
2
(x)t
+
3.1~(x)t
+
...
n=O
and
00
L
(k+l)P
k
+
I
(X)t
k
=
0+
lj(x)
+
2P
2
(x)t+313(x)t
2
+
...
k=-l

278
Special
Functions
actually give
the
same sum.
The
indices are sometimes referred
to
dummy
indices because they do
not
show up in the expanded expressions
and
can be
replaced with another letter.
If
we want to do so, we could now replace all
of
the k's with n's. The
second sum in equation
just
needs the replacement n = k
and
the last sum
we reindex using
k = n +
1.
Therefore, equation becomes
00
00
00
L
(k+l)P
k
+
I
(X)t
k
_L(2k+l)xP
k
(x)t
k
+LkPk_I(X)t
k
=
o.
k=-l
k=l k=l
We can now combine all
of
the terms, noting the k =
-1
term
is
zero
and
the k = 0 terms give
PI(x)
- xPo(x) =
o.
Therefore, for k > 0,
00
L[(k
+
1)Pk+l(x)-(2k
+
l)xP
k
(x)
+ kPk_I(X)]t
k
=
o.
k=l
Since this
is
true
for all t, the coefficients s
of
the tk's
are
zero,
or
(k
+
1)P
k
+
1
(x)
- (2k +
l)xP
k
(x)
+ kPk_l(x) =
0,
k =
1,
2,
....
There are
other
recursion relations.
For
example,
P On+1(x) - P'n_l(x) = (2n +
l)Pn(x).
This can be proven using the generating function by differentiating g(x,
t) with respect
to
x
and
rearranging the resulting infinite series
just
as in this
last manipulation.
Another
use
of
the generating function
is
to obtain the normalization
constant. Namely,
lIP
nf Squaring the generating function,
we
have
-1--2-:-t
+-t-::-
2
=
[t.,
Pn(x)t
n
r =
t.,~/n(X)Pm(X)tn+m
Integrating from
-1
to
1
and
using orthogonality, we have
= f
tt
2n
p;(x)dx.
n=O
However

Special
Functions
279
One can expand this expression
about
t = 0
to
obtain
!In(l+t)
=
f_
2
_t
2n
t
1-
t
n=O
2n
+ 1 .
Comparing this result with equation
we
find
that
liP
112
= r
P;(x)dx=_2_.
n
11
2n+
1
Finally,
we
can expand functions in this orthogonal basis. This
is
just a
generalized Fourier series. A Fourier-Legendre series expansion
forj(x) on
(-
I,
I)
takes the form
00
f(x)
~
LcnPn(x).
n=O
As with Fourier trigonometric series,
we
can determine the coefficients
s by multiplying
both
sides by P m(x)
and
integrating. Orthogonality give
the usual form for the generalized Fourier coefficients
s.
In
this case,
we
have
<f,P
n
>
C =
n
IiPn
112
.
2
We have
just
found
lIP
nll
2
= 2n + 1 . Therefore, the F ourier-Legendre
coefficients are
2n+l
r
c
n
=-2-
11f(x)Pn(x)dx.
Example:
Expandf(x)
= x
3
in a Fourier-Legendre Series.
We need
to
compute
2n+l
r 3
c
n
=-2-
11x Pn(x)dx.
We first note
that
LXmpn(x)dx
= 0 for m < n.
This
is
proven using Rodrigues formula in equation. We have
.L
1 f m d
n
2 n
xmp
(x)dx
=-
x
-(x
-1)
dx.
1 n 2nn! 1 dx
n
For
m <
n,
we
integrate by parts m-times and use the facts that Pn(l) = 1

280
Special
Functions
and
Pi-I)
= (_l)n.
The
right
hand
side vanishes.
As
a result, we will
have
that
c
n
= 0
for
n > 3
in
this example.
This
leaves
the
computation
of
co' c
t
'
c
2
and
c
3
.
Since x
3
is
an odd
function
and
Po
and
P
2
are
even functions,
Co
= 0
and
c
2
=
O.
This
leaves
us
with
only
two
coefficients s
to
compute.
These
are
c
t
= l r x
4
dx=l
2
il
5
71
3[1
3 ] 3
c
=-
x
-(5x
-3x)
dx=-
3 2 1 2
5·
Thus,
3 2
x3
=5l}(x)+5~(x)
.
.
Of
course, this
is
simple
to
check.
3 2 3
2[1
3 ]
-l}(x)+-~(x)
=-x+-
-(5x
-3x)
= x
3
5 5 5 5 2 .
Well,
maybe
we could have guessed this
without
doing
any
integration.
Let's
see.
Sincef(x)
= x
3
has degree three, we
do
not
expect
the
expansion
in
Legendre polynomials
forf(x)
to
have polynomials
of
order greater
than
three. So, we assume from
the
beginning
that
f(x)
= coPo(x) + CjPt(x) + c
2
Pz<x) + c
3
P
i
x
).
Then,
1 2 1 3
x
3
=Co
+Cl
x
+
"2
c2
(3x
-1)
+
"2C2(5x
-3x).
However,
there are
no
quadratic
terms
on
the
left side, so c
2
=
O.
Then,
there
are
no
constant
terms left except
co.
So,
Co
=
O.
This
leaves
1
3
x
3
= Clx+-C2(5x
-3x)
2
=(Cl -%C2
)+%
C2x
3
Equating
coefficients s
of
the
remaining
like
terms,
we
have
that
5 3 3
c2
="2
and
c
t
="2
c')
=5·
Example:
Expand
the
Heavisidefunction
in
a Fourier-Legendre Series.
In
this case, we
cannot
find
the
exparisi9n coefficients s
without
some
integration.
We
have
to
CQmpute
,
c = 2n+'1 r
f(x)Pn(x)dx
~'2n+I
r P
n
(x) dx
n 2
il
2
.h
Special
Functions
281
We can
make
use
of
the formula
for
n >
1.
Then,
I r I
P'
dx
1
c
n
=2"
.b[Pn+1(x)-
n-l(x)]
=2"[P
n
-
1
(0)-P
n
+
1
(0)].
For
n = 0, we have
C
=!rdx=!
o
2.b
2'
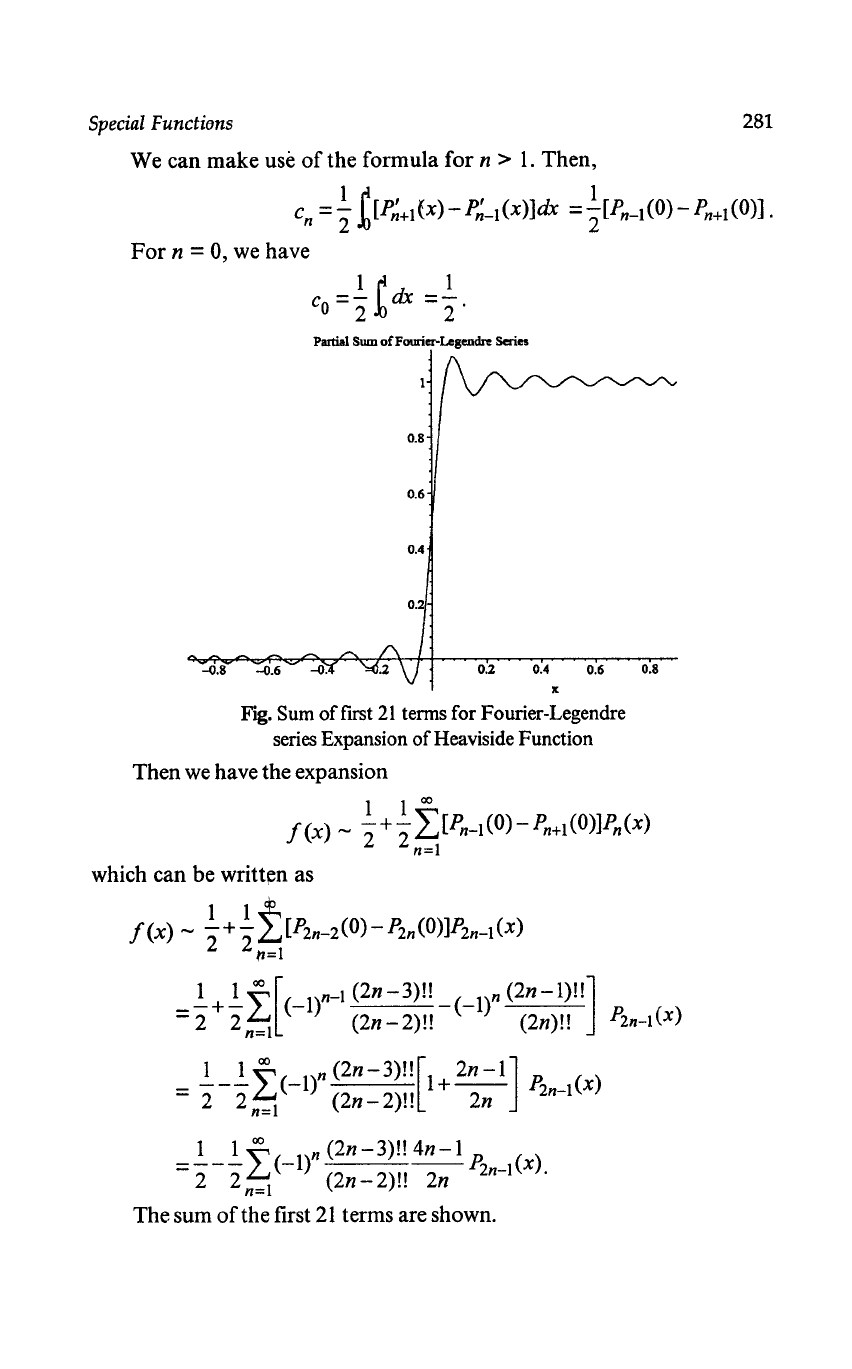
Partial Sum ofFourier-Lesenclre Series
0.8
0.6
0.4
0.2
-0.8
-0.6
0.2 0.4 0.6 0.8
x
Fig. Sum offirst
21
terms for Fourier-Legendre
series Expansion
of
Heaviside Function
Then we have the expansion
1 1
00
f(x)
-
-+-
~)Pn-l(O)-Pn+l(O)]Pn(x)
2 2
n=l
which can be
writt~n
as
f(x)
-
!+!
I[P2n-2(O)-P2n(O)]P2n-l(X)
2 2
t1=1
_!+!
~[(_l)n-l
(2n-3)!!
-(-It
(2n-l)!!]
- 2 2
~
(2n - 2)!! (2n)!! P
2n
-
1
(x)
_
!_!
~(_I)n
(2n-3)!![I+
2n-l]
p-
(x)
- 2
2~
(2n-2)!!
2n 2n-l
=!_!
~(-lt
(2n-3)!!
4n-l
p-
_ (x)
2
2~
(2n-2)!!
2n
2n
1 .
The sum
of
the first
21
terms are shown.
