Brewster H.D. Mathematical Physics
Подождите немного. Документ загружается.


212 Transform
Techniques
in Physics
This
is
the way we had found a representation
of
the Dirac delta
function previously. The Fourier transform approaches a constant
in
this limit.
As
a approaches zero, the sinc function approaches one, leaving
j (k)
~
2ab =
1.
Thus, the Fourier transform
of
the Dirac delta
function
is
one. Namely, we have
.c
o( x
)e
ikx
dx =
1.
In
this case
we
have that the more localized the function f (x)
is,
the more spread out the Fourier transform
is.
The Uncertainty Principle: The widths
of
the box function and its
Fourier transform are related
as
we have seen
in
the last two limiting
cases. It
is
natural to define the width, Ilx,
of
the box function as
Ilx
= 2a.
The width
of
the Fourier transform is a little trickier. This function
actually extends along the entire k-axis. However,
as j (k) becomes
more localized, the central peak becomes narrower. So,
we
define
the width
of
this function,
Me
as the distance between the first zeros
A 2b
on
either side
of
the main lobe. Since f (k) =T sin
lea,
the zeros
are at the zeros
of
the sine function, sin
lea
=
O.
The first zeros are
1t
at k = ± - . Thus,
a
21t
ilk=-.
a
Combining the expressions for the two widths, we find that
Ilxll.k =
41t.
Thus, the more localized a signal (smaller ox), the less localized its
transform (larger
ok).
This notion is referred to as the Uncertainty Principle. For more
general signals, one needs to define the effective widths more carefully,
but the main idea holds.
ilxilk
~
1.
While this is a result
of
Fourier transforms, the uncertainty principle
arises in other forms elsewhere. In particular, it appears in quantum
mechanics, where is it most known. In quantum mechanics, one finds that
the momentum
is
given
in
terms
of
the wave number, p = lik, where Ii is
Planck's constant divided by
21t.
Inserting this into the above condition,
one obtains

Transform
Techniques
in
Physics
!!.x/).p
~
h.
213
This gives the famous uncertainty relation between the uncertainties in
position and momentum.
{
e-
ax
x~O
Example:J(x) = , a>O
0,
x<O
The Fourier transform
of
this function is
j (k) =
LJ(x)e
ikx
dx
= r e
ikx
-
ax
dx
I
=--
a-ik·
Next, we will compute the inverse Fourier transform
of
this result and
recover the original function.
~
I
Example:
J(k)
=
---:-k
.
a-I
The inverse Fourier transform
of
this function is
J(x)
=
_I
F
j(k)e-ikxdk=_1
F
e-i~
dk.
2n Lo 2n
Lr:fJa-Ik
This integral can be evaluated using contour integral methods.
IfJ(z)
converges uniformly to zero as z
-7
I, then
lim
r J(z)eikzdz = 0
R~r:fJ
oCR
where
k>
0 and C R is the upper half
of
the circle
Izl
=
RA
similar result applies
for
k < 0, but one closes the contour in the lower half plane.
In
this example, we have to evaluate the integral
-ixz
1=
F_e_.
dz.
Lo
a-1Z
According to Jordan's Lemma, we need to enclose the contour with a
semicircle in the upper
half
plane for x < 0 and in the lower
half
plane for
x>
O.
The integrations along
th~
se!Dicircles· will vanish and we will have
I
e-
ixx
J(x)
=
2n
L
a-ik
dk

214
Transform
Techniques
in
Physics
1
e-
ixz
=
±_A
-dz
21t
'-!c
a - iz
{
O'
=
__
1-21ti Res[z
=-ia],
21t
=
{O~ax
e ,
x<O
x>O·
Example: ]
(ro)
=
n:o(ro
+
roo)
+
n:o(ro
-
roo).
x<O
x>O
We
would like to find the inverse Fourier transform
of
this function.
Instead
of
carrying out any integration,
we
will make use
of
the properties
of
Fourier transforms.
Since the transforms
of
sums are the sums
of
transforms, we can look
at each term individually.
Consider
o(ro -
roo).
This is a shifted function. From the Shift
Theorems we have
eiroO
t
fit)
H j
(ro
-
roo).
Recalling from a previous example that
.c
le
irot
dt
=
21to(
ro),
we have
F-1[o(
ro
-
roo)]
=
211t
e
-iroot
The other term can be transformed similarly. Therefore, we have
1 1
iroot
1
-iroot
F-
[1to(ro
+
roo)
+
1to(ro
-
roo]
= Ze +Ze = cos
root
{
COS
root,
It
I
::;;
a
Example: The Finite Wave
Train/(x)
= °
It
I > a
For our last example, we consider the finite wave train, which often
appears in signal analysis.
A straight forward computation gives
](ro)
=
r:
/(t)eirotdt
Transform
Techniques
in
Physics
=
fa
cos
root
cos
rot
dt
=
.!.
r [cos(
roo
+
roo)
t + cos(
roo
-
ro
)t dt]
2 a
sin(roo
+ro)a
sin(roo
-ro)a
=
+--'----
ro
+
roo
ro
-
roo
THE
CONVOLUTION
THEOREM -OPTIONAL
215
In
our
list
of
properties,
we
defined the convolution
of
two functions,
f (x) and g(x) to be the integral
(f
* g)(x) =
Lf(~)g(x-~)d~
In some sense one is looking at a sum
of
the overlaps
of
one
of
the
functions
and
all
of
the
shifted
versions
of
the
other
function. -i'he
German
word
for convolution is faltung, which means 'folding'. First,
we
note that the convolution is commutative. f * g = g * f This is easily
shown by replacing
x -
~
with a new variable, y.
= _
[Xl
g(x-
y)f(y)dy
= -
Lf(y)g(x-
y)dy
=
(f
* g) (x).
Example:
Graphical
Convolution.
In order to understand the convolution operation,
we
need to apply it to
several functions.
We
will do this graphically for the box function
{
I,
Ixl
< 1
f(x)=
0,
Ixl>!
and
the
triangular
function
{
X,
Ixl<l
g(x) = 0,
Ixl
>!
.
In
order
to determine the
~ontributions
to the integrand,
we
look at
216 Transform Techniques in Physics
the shifted and reflected function
g(~
-
x)
for various values
of
~.
For
~
= 0, we
Box Fuction
0.8
0.6
0.4
0.2
-4
-2
0
2 x
4
Fig. A Plot
of
the Box
Function/(x)
Triangli
"'unction
0.8
0.6
0.4
0.2
-4
-2
u
2x
4
Fig. A Plot
of
the Triangle Function
Reflected Triangle Function
1
O.B
J.6
l
--4
-2
0
:1
x
4
~
Fig. A Plot
of
the Reflected Triangle Function
Transform
Techniques
in
Physics
Shifted, Reflected triangle Function
1
0.8
0.6
0.4
0.2
-4
-2
2 x
4
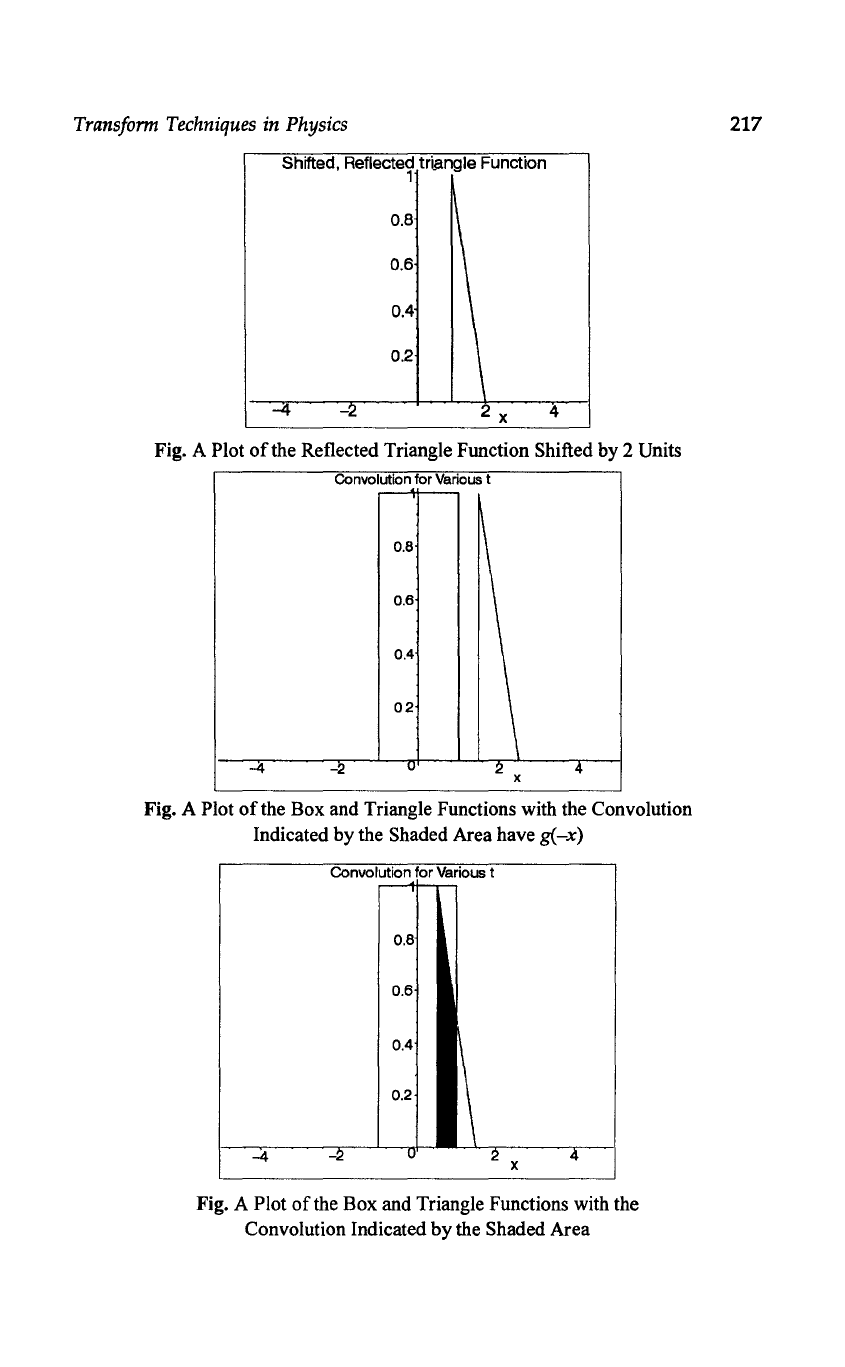
Fig. A Plot
of
the Reflected Triangle Function Shifted by 2 Units
Convolution for Various t
0.8
0.6
0.4
02
-4
-2
u
2 x
4
Fig. A Plot
of
the Box and Triangle Functions with the Convolution
Indicated
by the Shaded Area have
g(-x)
Convolution
for
Various t
0.8
0.6
0.4
1\
0.2
-4
-2
u
2
x
4
Fig. A Plot
of
the Box and Triangle Functions with the
Convolution Indicated
by
the Shaded Area
217
218 Transform Techniques in Physics
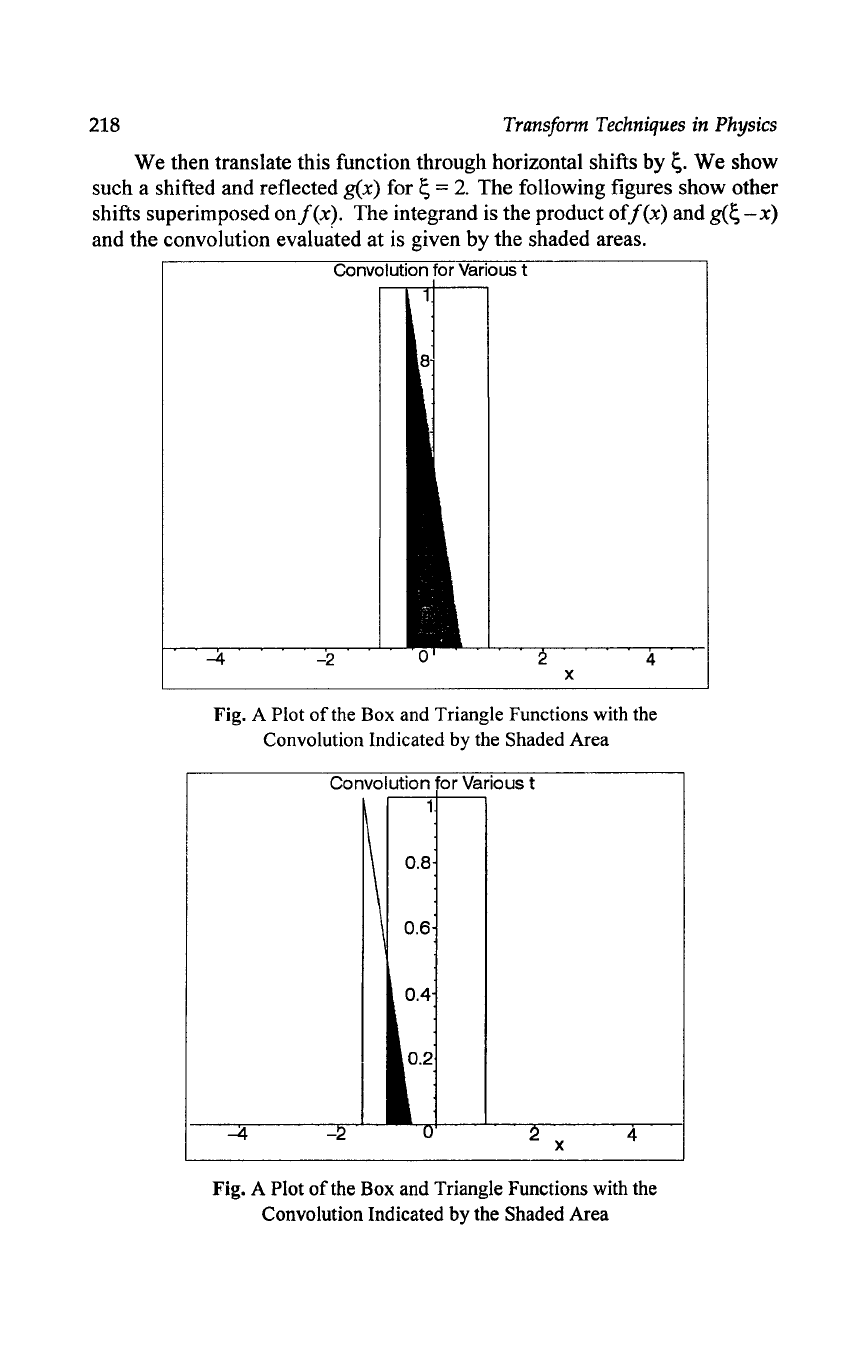
We
then translate this function through horizontal shifts
by~.
We
show
such a shifted and reflected g(x) for
~
=
2.
The
following figures
show
other
shifts superimposed onJ(x). The integrand is the product
ofJ(x)
and
g(~
-x)
and
the
convolution evaluated
at
is given by
the
shaded areas.
x
Fig. A Plot
of
the
Box and Triangle Functions
with
the
Convolution Indicated
by the Shaded Area
Fig. A Plot
of
the Box and Triangle Functions with the
Convolution Indicated
by
the Shaded Area

Transform
Techniques
in
Physics
-4
Convolution for Various t
0.8
0.6
0.4
0.2
-2
u
2
X
Fig. A Plot
of
the Box and Triangle Functions
with the Convolution Indicated
by
the Shaded Area
219
4
The area is zero, as there is
no
overlap
of
the functions. Intermediate
shift values are displayed in figures and the convolution is shown by the area
under the product
of
the two functions.
-4
Convolution
of
Block & Triangle Functions
0.5
0.4
0.3
0.2
0.1
-2
o
2 t
4
Fig. A Plot
of
the Convolution
of
the Box and Triangle Functions

220
Transform
Techniques
in
Physics
We see that the value
of
the convolution integral builds up and then quickly
drops to zero. The plot
of
the convolution
of
the box and triangle functions is
given.
Next we would like to compute the Fourier transform
of
the convolution
integral. First, we use the definitions
of
Fourier transform and convolution to
write the transform as
F
[f
* g] =
[00
(f
*
g)
(x)e
ikx
dx
=
.c
.cf(t)g(x-~)d~eikx
dx
=
.c(
foog(x-~)eikx
dx
)f(~)d~.
Next, we substitute y = x -
~
on the inside integral and separate the
integrals.
F
[f*
g] =
r:(
r:g(x-~)eikx
dx
)f(~)d~
.c(
r:g(y)eik(Y+~)
dy
)f(~)d~
foo(
r:g(y)e
iky
dy
)f(~)eik~d~
= (
foof(x)eik~
d~)
(
r:
g(y)e
iky
d
Y
).
We see the the two integral factors are
just
the Fourier transforms
off
and g. Therefore, the Fourier transform
of
a convolution is the product
of
the
Fourier transforms
of
the functions involved.
Fit
* g] =
j(k)g(k).
Example: Convolution
of
two Gaussian functions.
We will compute the convolution
of
two Gaussian functions with
different widths. Let
f (x) =
e-ax2
and g(x) =
e-
bx2
. A direct evaluation
of
the integral would be to compute
(f
* g)(x) =
.cf(~)g(x-~)d~
=
.c
e-ae-b(x-~)2
d~
This integral can be rewritten as
i
r'
2
(f
* g)(x)
=e-
bx
100
e-(a+b)~
+2bx~d~.

Transform Techniques in Physics 221
One could proceed to complete the square
and
finish carrying
out
the integration. However, we will use the Convolution Theorem to evaluate
the convolution. Recalling the Fourier transform
of
a Gaussian, we have
~
2
~
k2/2
f(k)
=
F[e-ax
]=V--;e-
a
and
g(k)
=F[e-
bx2
] =
J¥
e-
k2
12b
Denoting the convolution function by h(x) =
(j
* g)(x), the Convolution
Theorem gives
~
f~(k)
~(k)
21t
-k
2
/2b
-k
2
/2b
h(k)
= g =
Me
e .
This is another Gaussian function, as seen
by
rewriting the Fourier
transform
of
h(x) as
1(1
I)
2 b
~ ~
21t
--
-+-
k
21t
_~k2
h(k)
=
h(k)
=
--e
2 a b =
--e
2ab
M M
To complete the evaluation
of
the convolution
of
these two Gaussian
functions, we need to find the inverse transform
of
the Gaussian in equation.
We have first that
rl[
J¥e-
k212
,]
~e-~2.
Moving the constants, we then obtain
F-I[e-k2/2a]
=
Jife-
ax2
.
1
We now make the substitution a = 2a '
2
~
-x
2
/2a
F-1
[
-ak
] = - e .
e
41tU
a+b
This is in the form needed to invert. Thus, for a = 2ab we and
21t
--x
H£
ab
2
(j*
g)(x) = h(x) =
--e
a+b
a+b
