Brewster H.D. Mathematical Physics
Подождите немного. Документ загружается.


182
and
Complex
Representations
of
Functions
Res[-2-
I
-;
z =
1]
=
lim
(z
-1)-2
1
-
z
-1
z~l
z
-1
=
lim-I-=!
=~lz+1
2'
Res
[-2-
1
-;
z = I] =
lim
(z +
1)+
z
-1
z~l
z
-1
=
lim
_I_=_!
z~-lz-I
2'
£
Q7t
de
Example: 2 e .
+cos
Here we have a real integral in which there are
no
signs
of
complex
functions.
In
fact,
we
could apply methods from
our
calculus class
to
e
do
this integral, attempting
to
write I + cos e = 2 cos
2
"2'
We
do
not,
however, get very far.
iy
-4
-3
-2
-1
1 x
-i
Fig.
Contour
for
Computing~=1=2
z~
1
One trick, useful in computing integrals whose integrand
is
in the
form!
(cos
e,
sin
e),
is
to
transform the integration to the complex plane through the
transformation
z = e
iS
. Then,
e
iS
+ e
-is
1 ( 1 )
cos e =
=-
z+-
2 2
z'
e
iS
_ e
-is
i ( 1 )
sin e = 2 =
-~
z - -; .

Complex
Representations
of Functions
183
Under
this transformation, z = ei9, the integration now takes place
around
the
unit circle in
the
complex plane.
Noting
that
dz =
ie
i9
de = iz
de;
we have
f1t
de
.b
2
+cose
dz
A dz
=
-l'jlzl=l
2 1
(2
1)
z+-
z +
2
2.r!
-
dz
=-
''jjzl=l
z2+4z+1·
We
can
apply
the
Residue
Theorem
to
the
resulting integral.
The
singularities occur for
z2
+
4z
+ 1 =
o.
Using the
quadratic
formula, we
have
the
roots z =
-2
±
J3
. Only z =
-2
+
J3
lies inside
the
integration.
-2i
contour.
We
will therefore need
the
residue ofJ(z) = 2 simple
at
. z
+4z+1
this pole:
2
·
1·
z-(-2+J3)
- - I
1m
-
Z-7-2+J3(z-(-2+J3))(z-(-2-J3))
2
·
1·
1
- - I
1m
-
Z-7-2+J3(z-(-2-J3)
-2i
3

184
Complex
Representations of
Functions
Therefore, we have
r21t
de
=
-2irf
dz =
2TCi(
-i.fiJ
=
2TC.fi
.b
2+cose
'1jzl=lz2+4z+1
'3
3'
2
rf
z +1 d
Example:
'1l
z
l=3
(z _1)2(z + 2)
z.
In
this example there are two poles z =
1,
-2
inside the contour.
z = 1
is
a second order pole
and
z = 2
is
a simple pole. Therefore,
we
need
z2 + 1
the residues
at
each pole for fez) =
(z
-li(z
+
2)
:
. _ _
lim!~
(z_I)2
z
+1
[
2
1
Res[f(z), z -
1]
-
z~ll!dz
(z_I)2(z+2)
_ lim(Z2+
4Z
-
1
J
-
.z~l
(z
- 2)2
4
-9'
3 x
-3i
Z2
+1
Fig.
Contour
for
Computing
c
~=1=3
(z
-1)2(z
+ 2) dz
z2
+1
Res[f(z) z = -2] =
lim
(z +
2)
2
,
z~-2
(z-l)
(z+2)
2
_
lim
z +1 = 5
-
z~-2(z_2)2
9 .
The evaluation
of
the integral
is
now
2TCi
times the sum
of
the residues .
.
rf
z2
+ 1 dz _
2TCi(~+~)
-
2TC'
'1jz/=3
(z
_1)2(z + 2) - 9 9 -
l.

Complex
Representations of
Functions
COMPUTING
REAL
INTEGRALS
185
As
our
final application
of
complex integration techniques, we will
turn to
the evaluation
of
infinite integrals
of
the form L
f(x)dx
. These
types
of
integrals will appear later in the text
and
will help to tie in
what
seems
to
be a digression in
our
study
of
mathematical physics.
In
this
section
we
will see
that
such integrals may be computed by extending the
integration to a
contour
in the complex plane.
Recall that such integrals are improper integrals
and
you had seen them
in your calculus classes. The way
that
one determines
if
such integrals exist,
or
converge,
is
to
compute the integral using a limit:
.c
f(x)dx
=
1~00
fR
f(x)cIx
For
example,
F
_1
dx =
lim
[R
_1
cIx=
lim
(-~J
=
o.
loo
x
2
R~oo
R x
2
R~oo
R
Similarly,
. R .
(R2
(_R
2
))
F xcIx =
hm
[ xcIx= hm
----
=
o.
100
R~oo
R
R~oo
2 2
However, the integrals
r xcIx and
foo
xcIx do
not
exist.
Note
that
i xcIx = hm
r'
xcIx= hm -
=00
.
. R .
(R2)
.b
R~oo
.b
R~oo
2
Therefore,
Lf(x)cIx
=
Lf(x)cIx+
r
f(x)cIx.
does
not
exist while
limR~
00
fRf(X)cIx
does exist. We will be interested
in computing
the
latter
type
of
integral. Such
an
integral
is
called the
Cauchy
Principal
Value
Integral
and
is
denoted
with either
a P
or
PV
prefix:
P
Lf(x)dx
=
1~00
fRf(X)cIx.
In
our
discussions
we
will be computing integrals over the real line
in
the
Cauchy principal value sense.

186
Complex
Representations
of
Functions
We
now proceed to the evaluation
of
such principal value integrals using
complex integration methods.
We
want to evaluate the integral
Fig. Contours for Computing P
[,f(x)dx
[J(x)dx.
We will extend this into an integration in the complex
plane.'
We extend
J (x) to f{z) and assume that f{z) is analytic in the upper
half plane
(Im(z) > 0). We then consider the integral
fRJ(x)dx
dx as an
integral over the interval
(-R,
R).
We
view
this
interval
as a
piece
of
a
contour
CR
obtained
by
completing the contour with a semicircle
-R
of
radius R extending into
the upper
half
plane.
Note, a
similar
construction
is
sometimes
needed
to
extend
the
integration into the lower half plane (Im(z) < 0) when.f{z) is analytic there.
The integral around the entire contour
CR
can be computed using the
Residue Theorem and is related to integrations over the pieces
of
the
contour by
rC
J(z)dz
= r
J(z)dz
+
[ll.
J(z)dz.
'1c
R
..r
R
R
Taking the limit R
~
00
and noting that the integral over (-R, R) is
the desired integral, we have
p [ooJCx)dx =
4cJcz)dz-lR
J(z)dz
,
where we have identified C as the limiting contour as R gets large,
rC
JCz)dz = lim
rC
JCz)dz.
'1c
R
~oo
'1c
R
Now the key to carrying out the integration
is
that the integral over
r R
vanishes
in
the
limit.
This
is
true
if
Rif
(z)1
~
0
along
r R as
R~l.

Complex
Representations of
Functions
-R
-/
Fig. Contour for Computing
i'
dx
2
L",
l+x
187
This can be seen by the following argument. We can parametrize the contour
r R using z = Re
i9
. We assume that the function is bounded by some function
of
R. Denote this functon by M (R). Thus, for
If{z)1
< M (R), we have
Il
R
f(Z)dzl
=lf1t
f(Rei9)Rei9del
~
f
1t
lf(Re
I9
)lde
<
RM(R)
f1t
de
= 21tRM(R).
So,
if
limR-.~oo
RM
(R) =
0,
then
limR~oo
l R
f(z)dz
=
0.
We
show how this applies some examples.
Example: Evaluate L 1 dx 2 .
+x
We already know how
to
do
this integral from our calculus classes.
We have that
r
dx
2 = lim
(2tan-
1
R) =
2(2:)
= 1t.
Lo
1
+x
R~oo
2
We will apply the methods
of
this section and confirm this result.
The poles
of
the integrand are at z = ±i.

188 Complex Representations
of
Functions
~-:\
i 1 \ \
-R
-e
R
.c
sinx
Fig.
Contour
for
Computing
P
--dx
ro x
1
We
first note
thatfiz)
=--2
goes to zero fast enough on r R
as
R gets
l+z
large.
R R
R[f(z)! = =
---;======
11
+ R
2
e
2i8
I
~I
+
R2
cose +
R4
Thus,
as
R
~
00
1,
Rfiz)
~
o.
So,
rodx
,rdz
loo
1 + x
2
=
ic
1 +
z2
.
We
need only compute the residue at the enclosed pole, z = i.
1
·
(
.)
1
1·
1 1
Res[f(z), z = i] =
UTI
Z-1
--=
Im--.
=--:-
Z~1
1 +
z2
Z~l
z + 1 21
Then, using the Residue Theorem, we have
(
smx
Example: P
--dx
.
00
x
=1t
There are several new techniques that have to be introduced in order
to carry out this integration.
We need to handle the pole at
z = 0
in
a special way and we need
something called Jordan's Lemma to guarantee that the contour on the
contour
r R vanishes, since the integrand does not satisfy our previous
condition on the bound.
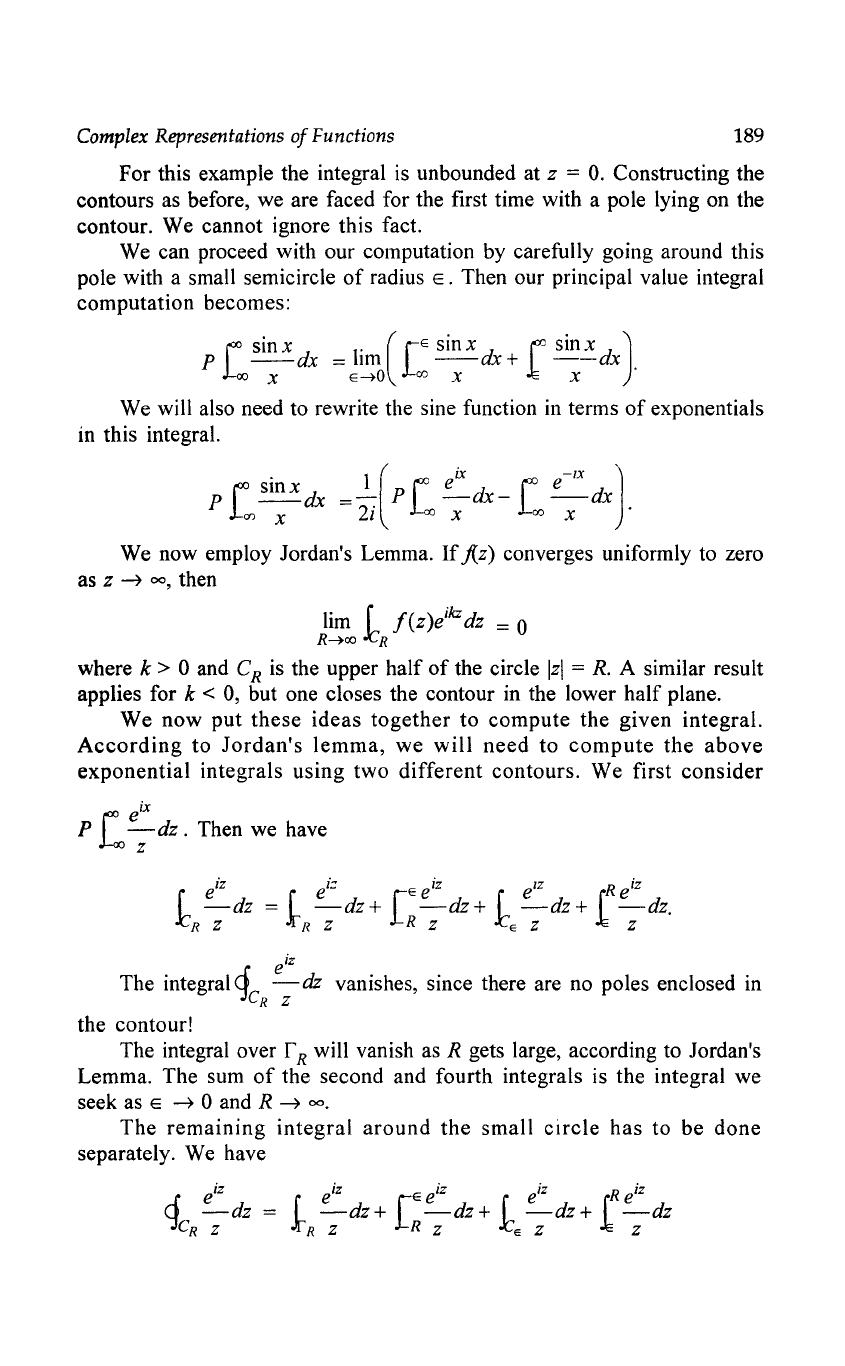
Complex
Representations
of Functions
189
For this example the integral is unbounded at z =
O.
Constructing the
contours as before, we are faced for the first time with a po
Ie
lying on the
contour. We cannot ignore this fact.
We
can proceed with our computation by carefully going around this
pole with a small semicircle
of
radius
E.
Then our principal value integral
computation becomes:
(
sin
x
I'
([E
sin x
dx
r sin x d J
p
--dx
=
1m
--
+
--
x .
00
X E~O
00
X X
We
will also need to rewrite the sine function in terms
of
exponentials
in this integral.
(
sin
x 1 ( F e
ix
Fe-IX
'J
p
--dx
=---:
p
100
-dx-
L
-dx
.
if)
x
21
X
00
X
We now employ Jordan's Lemma.
If
j(z) converges uniformly to zero
as
z
~
00,
then
lim
r
f(z)e
ikz
dz = 0
R~oo
.tR
where k > 0 and C R is the upper half
of
the circle
Izl
= R. A similar result
applies for
k < 0, but one closes the contour in the lower half plane.
We now put these ideas
together
to compute the given integral.
According
to
Jordan's
lemma,
we
will
need
to
compute
the
above
exponential integrals using two different contours. We first consider
F e
ix
p
100
-;dz.
Then we have
/z
ei::
E e
iz
e
'Z
R e
iz
r
-dz
= r
-dz+
[
-dz+
r
-dz+
r'
-dz
.
.tR
z
Jr-
R Z R Z
kE
Z
.b
z
e
iz
The integral
rr
-dz
vanishes, since there are no poles enclosed in
'-JC
R
z
the contour!
The integral over
r R will vanish as R gets large, according to Jordan's
Lemma. The sum
of
the second and fourth integrals is the integral we
seek as
E
~
0 and R
~
00.
The
remaining
integral
around
the
small
circle
has to be done
separately.
We
have
iz
eiz E e
iz
e
iz
R e
iz
rr
~dz
= r
-dz+
[
-dz+
r
-dz+
r'
-dz
'-Jc
R z
.lr
R Z R Z
kE
Z
.b
z
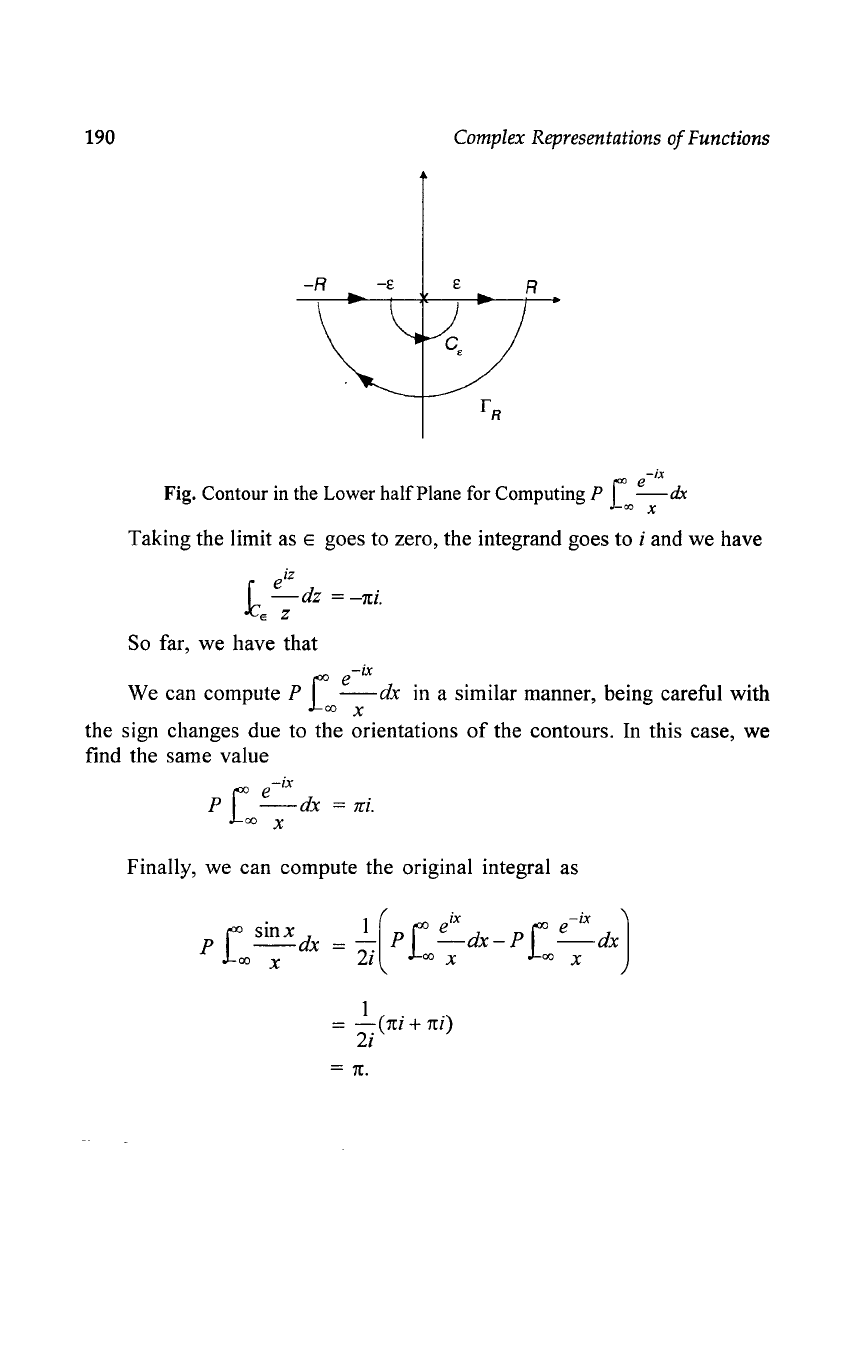
190
Complex
Representations of Functions
-ix
Fig. Contour in the Lower
half
Plane for Computing P [
_e_
dx
00
x
Taking the limit as E goes to zero, the integrand goes to i and we have
e
iz
1-
dz
=
-1ei.
E z
So far, we have that
-Ix
We can compute P
r'
_e_
dx
in a similar manner, being careful with
LXl
x
the sign changes due to the orientations
of
the contours.
In
this case, we
find the same value
[
e-ix
.
P
--dx
= 7rl.
<Xl
X
Finally, we can compute the original integral as
r'
sinx
d =
~[P.c
e
ix
dx-P.c
e-
ix
dXJ
P
l<Xl-x-
X
21
<Xl
X
<Xl
X
1
=
2/
ni
+
nO
=
n.

Chapter 6
Transform
Techniques
in
Physics
INTRODUCTION
Some
of
the most powerful tools for solving problems
in
physics are
transform methods.
The
idea is
that
one
can
transform the
problem
at
hand to a new problem in a different space, hoping that the problem in the
new space is easier to solve. Such transforms appear in many forms.
The Linearized Kdv Equation
As a relatively simple example, we consider the linearized Kortweg-
deVries (KdV) equation.
U + cu +
AU
= 0
-00
< X <
00
t x P
xxx'
.
This equation governs the propagation
of
some small amplitude water
waves. Its nonlinear counterpart has been at the centre
of
attention in the
last
40 years as a generic nonlinear wave equation.
We seek solutions that oscillate
in
space. So, we assume a solution
of
the form
u(x,
t)
=
A(t)e
ikx
In
that
case, we found plane wave solutions
of
the form eikCX - ct),
which we could write as ei(kx-rot) by defining
co
=
kc.
We further note that
one often seeks
complex
solutions
of
this form and
then
takes the real
part in order to obtain a real physical solutions.
Inserting the guess into the linearized KdV equation, we find that
~
+i(ck-~k3)A
=
O.
Thus,
we
have converted
our
problem
of
seeking a solution
of
the
partial
differential
equation
into
seeking
a
solution
to
an
ordinary
differential equation. This new problem is easier to solve. In fact, we have
AU)
=
A(0)e-
i
(ck-k3)1.
Therefore, the solution
of
the partial differential
~quation
is
u(x,
t)
= A(0)e
ik
(X-(C-
P
k
2
)t)
•
We note that this takes the form
ei(kx-wt),
where
co
=
ck-
p~.
