Brewster H.D. Mathematical Physics
Подождите немного. Документ загружается.


162
Complex
Representations
of
Functions
2
Fig. The Integral
~C
J(z)dz
Around C
is
zero
if
the Integral fr
J(z)dz
is
Path Independent
Assuming that the integrals from point I to point 2 are path independent,
then the integrals
overCl
and C-
2
are equal. Therefore, we have
<}cf(z)dz
=
o.
Cauchy's Theorem
Next we investigate
if
we can determine that integrals over simple closed
contours that vanish without doing all the work
of
parametrizing the contour.
First, we need to establish the direction about which we traverse the contour.
Definition: A curve with parametrization
(x(t), y(t» has a normal
(nx' ny) = ( -
~;
, :
).
Recall that the normal
is
a perpendicular to the curve. There are two
such perpendiculars. The above normal points outward and the other normal
points toward the interior
of
a closed curve. We will define a positively oriented
contour as one that
is
traversed with the outward normal pointing to the right.
As one follows loops, the interior would then be on the left. As an example,
the contours in figure are positively oriented.
We now consider
<}c(u
+
iv)dz
over a simple closed contour. This can
be
written in terms
of
two real integrals in the xy-plane.
C}C
(u + iv)dz = 1 (u + iv)(dx + idy)
iudx-vdy+
i i
vdx+udy.
These integrals in the plane can
be
evaluated using Green's Theorem in
the Plane. Recall this theorem from your last semester
of
calculus.
Theorem: Green's Theorem in the Plane.

Complex
Representations of Functions
163
Let
P(x,
y)
and
Q(x,
y) be continuously differentiable functions on and
inside
the
simple
closed
curve
C.
Denoting
the
enclosed
region S,
we have
1
Pdx
+Qdy =
Hs(~;
-
:)dxd
Y
.
Using Green's Theorem to rewrite the first integral, we have
1udx-vdy
=
Hs(
-:
-:
)dxd
Y
.
If
u and v satisfy the Cauchy-Riemann equations,
au
av av
au
ax
dy'
ax
dy'
then the integrand
in
the double integral vanishes. Therefore,
1
udx
-
vd
y = 0
In
a similar fashion, one can show that
1
vdx
-
ud
y =
o.
We have thus proven the following theorem.
Theorem
If
u and v satisfy the Cauchy-Riemann equations inside and
on the simple closed contour
C,
then
1(U+iV)dz
=0.
Fig. The Contours Needed to Prove
that1cf(z)dz
=gcf(z)dz.
whenj(z) is
Holomorphic between the Contours C and
C'
Corollary:
1c/(z)dz
= 0
when/is
differentiable
in
domain D with C p
D.
Either one
of
these is referred to as Cauchy's Theorem.

164
Complex
Representations
of
Functions
Example: Consider
~Z_II=3z4
dz. SinceJ(z) =z4 is differentiable inside
the circle
I z - 1 I = 3, this integral vanishes.
We
can use Cauchy's Theorem to show
that
we
can deform one contour
into another, perhaps simpler, contour.
Theorem: Ifj(z) is holomorphic between two simple closed contours, C
and
C', then
qeJ(z)dz
=qe,/(z)dz.
We
consider the two curves, now connect the
two
contours with contours
f 1 and f 2 as shown. This splits C into contours
Cl
and C2 and
C'
into contours
C'I and C'2·
j(z) is differentiable inside the newly formed regions between the curves
and
the boundaries
of
these regions are
now
simple closed curves.
Therefore, Cauchy's
Theorem
tells us
that
integrals
of
j(z) over these
regions are zero. Noting that integrations over contours in the opposite direction
introduce a negative sign, we have from Cauchy's Theorem that
and
In the first integral
we
have traversed the contours in the following order.
C
I
,
fI'
C'I backwards and f
2
.
The
second integral denotes the integration
over the lower region, but going backwards over all contours except for C
2
.
Adding these
two
equations,
we
have
lIJ(z)dz+
tJ(Z)dZ-l;J(Z)dz-12J(z)dZ
= 0
Noting that C = C
I
+ C
2
and
C'
= C
1
+ C
2
,
we
have
qe
J(z)dz
=
qe
l
J(z)dz,
as was to be proven.
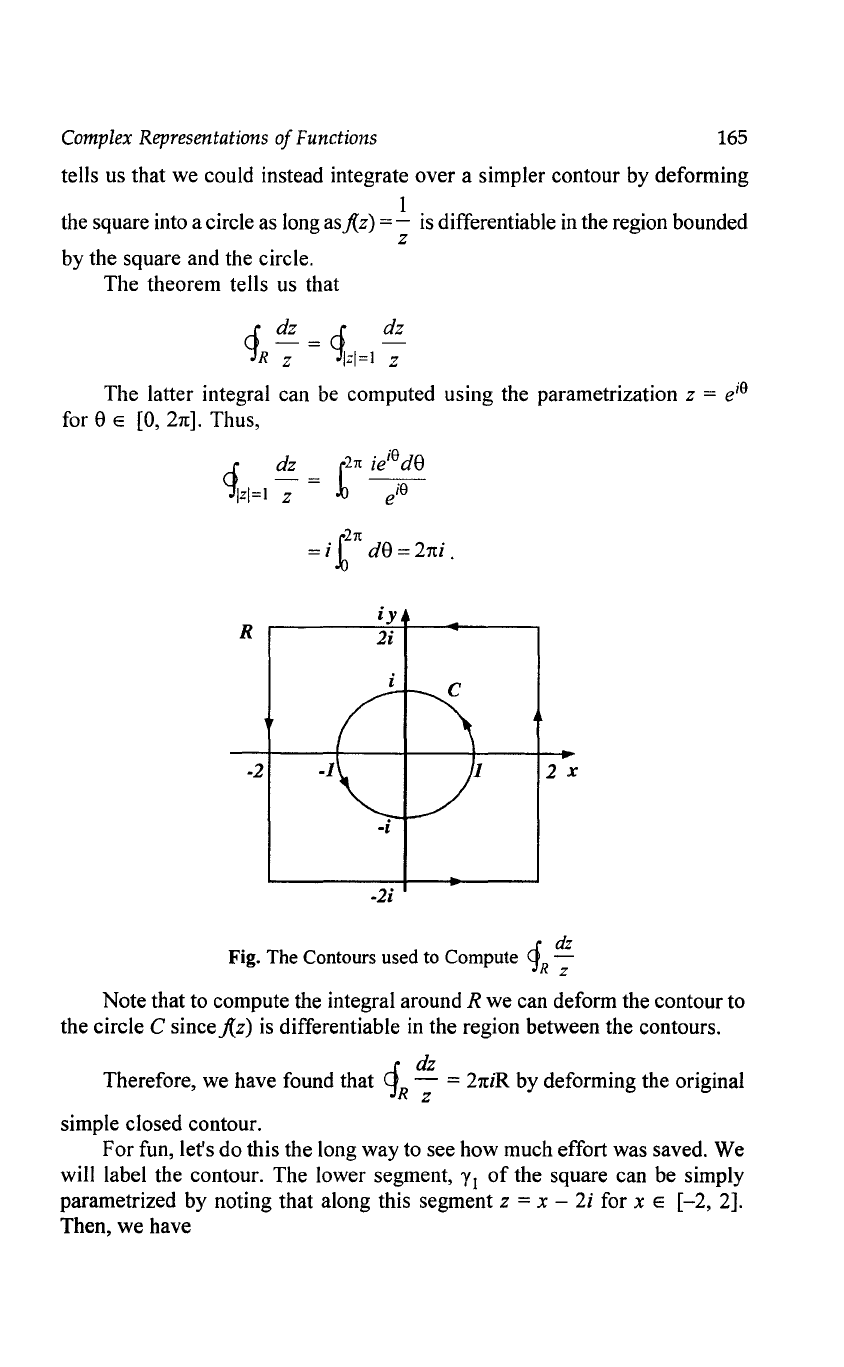
,-{
dz
Example: Compute'jR
-;-
for R the rectangle
[-2,
2] X [-2i, 2i].
We
can do this integral
by
computing four separate integrals
over
the
sides
of
this square in the
complex
plane.
One
simply parametrizes
each
line
segment, performs
the
integration and sums the four results. The last
theorem
Complex
Representations of
Functions
165
tells us that we could instead integrate over a simpler contour by deforming
1
the square into a circle as long
asj(z) = - is differentiable in the region bounded
z
by the square and the circle.
The theorem tells us that
4R
~
=
1=1=1
~
The latter integral can be computed using the parametrization z = e
i9
for e E [0,
21t].
Thus,
,.(
dz
=
r21t
iei~
de
irzi
= 1 z
.b
eta
r21t
=
i.b
de =
21ti
.
R
iy
2i
-2
-1
2x
-2i
rC
dz
Fig. The Contours used to Compute
'fR-;
Note that to compute the integral around R we can deform the contour to
the circle C sincej(z)
is
differentiable
in
the region between the contours.
cf
dz
Therefore, we have found that - =
21tiR
by deforming the original
R z
simple closed contour.
For fun, let's
do
this the long way to see how much effort was saved. We
will label the contour. The lower segment,
y 1
of
the square can be simply
parametrized by noting that along this segment z
= x - 2i for x E
[-2,
2].
Then,
we
have
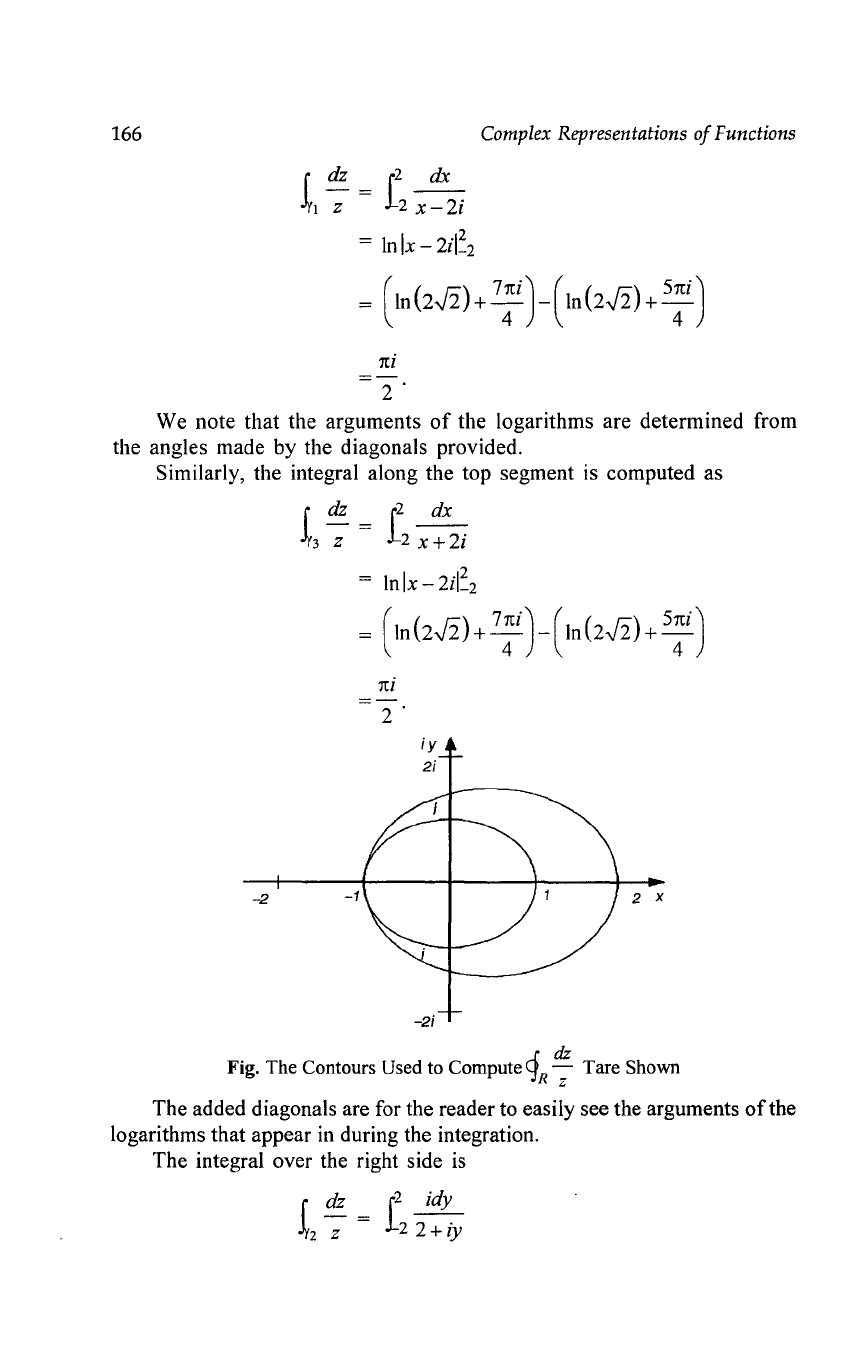
166
f dz _
r2
~
Jy,
z
12
x-2i
=
In
Ix
- 2il:2
Complex
Representations of
Functions
=
(In
(2J2)+ 7:i)_(ln(2J2)+
5:i)
1[i
2·
We note
that
the arguments
of
the logarithms are determined from
the angles made by the diagonals provided.
Similarly, the integral along the top segment is computed as
f3
dz
z
=
r2
dx
Jy
12
x+2i
lnlx - 2il:2
(In
(2J2)+ 7:i)_(ln(2J2)+
5:i)
2·
-2
-1
iy
2i
-2i
2 x
Fig. The Contours Used to Compute
gR
~
Tare Shown
"-
The added diagonals are for the reader to easily see the arguments
of
the
logarithms that appear in during the integration.
The integral over the right side is
f dz
r2
idy
Jy2
-;
=
12
2 + iy

Complex
Representations of Functions
=
In
12
+
iyl=2
=
(In(2J2)+
~)-(ln(2J2)+
~)
1ti
2'
Finally, the integral over the left side
is
r dz = f idy
Jy4
z 2
-2
+
iy
Inl2 +
iyl=2
(In
(2J2)
+
5:i)
_ (In
(2J2)
+
3:i)
1ti
2'
Therefore, we have that
cfR
~
=
4(
~)
= 21ti,
167
Note that we had obtained the same result using Cauchy's Theorem.
However, it took quite a bit
of
computation!
The converse
of
Cauchy's Theorem
is
not true, namely
cfc
f(z)dz
= 0 does
not imply
thatfiz)
is
differentiable. What we do have though,
is
Morera's Theorem.
Theorem:
Letfbe
continuous
in
a domain
D.
Suppose that for every simple
closed contour C
in
D,
cf
c
f(z)dz
=
O.
Thenfis
differentiable
in
D. The proof
is
a bit more detailed than we need to go into here. However, this result
is
used in the next section.
Analytic Functions and Cauchy's Integral Formula
In the previous section we saw that Cauchy's Theorem was useful for
computing certain integrals without having to parametrize the contours,
or deforming certain contours to simpler ones. The integrand needs to
possess certain differentiability properties. In this section, we will generalize
our integrand slightly so that we can integrate a larger family
of
complex
functions. This will take the form
of
what
is
called Cauchy's Integral

168
Complex
Representations of Functions
Formula, which is different from Cauchy's Theorem.
We
first
need
to
explore
the
concept
of
analytic functions.
Definition: j(z) is analytic in D
if
for every open disk
Iz
-
zol
< p lying in
D,j(z)
can be represented as a power series in
zOo
Namely,
00
J(z)=
Lcn(z-zo)n
n=O
This
series
converges
uniformly
and
absolutely
inside
the
circle
of
convergence,
Iz
-
zol
<
R,
with
a radius
of
convergence
R.
Since j(z) can be written as a uniformly convergent
power
series,
we
can
integrate
it
term
by
term
over
any
simple
closed
contour
in D
containing
z00
In
particular,
we
have
to
compute
integrals
like
4c
(z
-
zot
dz .
As
we
will
see
in
the
homework
exercises,
these
integrals evaluate to zero. Thus,
we
can
show
that.
Theorem:
For
j(z) analytic in D
and
any
C lying in
D,4c
J(z)dz
=
O.
Also, J is a
uniformly
convergent sum
of
continuous
functions, so
j(z)
is
also
continuous.
Thus,
by
Morera's Theorem,
we
have
that
j(z) is differentiable
if
it is
analytic:
Often terms like analytic, differentiable and holomorphic are used
interchangeably, though there is a subtle distinction
due
to
their definitions.
Let's
recall
some
manipulations
from
the
study
of
series
of
real
functions.
The
reader might need to recall
how
to sum geometric series. A
review is given
at
the end
of
this section. Essentially,
we
will make repeated
use
of
the result
a
---
,
a-r
1
Example:
j(z)
=--
for
Zo
=
O.
l+z
Irl
<
1.
This
case
is simple.
j(z)
is
the
sum
of
a geometric series for
Izl
<
1.
We
have
lOOn
j(z)=
-=
LC-z)
1 + z
n=O
Thus,
this
series
expansion
converges
inside
the
unit
circle
in
the
complex
plane. '
1 1
Examnle:
j(z)
=--
for z
--
r
l+z
0-2'

Complex
Representations of
Functions
169
We now look into an expansion about a different point. We could
compute
the
expansion
coefficients
using
Taylor'
formula
for
the
coefficients. However, we can also make use
of
the formula for geometric
series after rearranging the function. We seek an expansion
in
powers
of
1
z
-"2'
So, we rewrite the function
in
a form that has this term. Thus,
1 1 1
fez) =
17;
= ( 1
1)
= 3 (
1)
1+
z-2+2
2+
z-2
This
is
not
quite
in the form we need.
It
would
be nice
if
the
denominator were
of
the form
of
one plus something.
3
We
can get the denominator into such a form by factoring out the 2 .
Then we would have
2 1
fez) = 3 3 (
1)
.
1+-
z--
2 2
x
1 1
Fig. Regions
of
Convergence for Expansions
off{z)
0=-
z
0=
0 and z
0=-
l+z
2
1
The second factor now has the form
1-
r ' which would
be
the sum
of
a
geometric series with first term
a = 1 and ratio r = -
~(z
-
~)
provided that
Irl
<
1.
Therefore, we have found that
2°O[
2(
1)]n
f(z) =
3,7;
-3
z-2

170
for
Complex
Representations
of
Functions
/-%(
z-~)/
< 1.
This convergence interval can be rewritten as
/
z
_.!./
<i
2
2·
1 3
This
is
a circle centered at z
=2
with radius
2.
We show the regions.
of
convergence for the power series expansions
1 1
of
f(z)
= 1 + z about z = 0 an d z =
2.
We note that the first expansion
gives
us
thatf(z)
is
at
least analytic inside the region
Izl
<
1.
The second expansion shows
that
fez)
is
analytic in a region even
further outside
to
the region
lz
-
~l
<
~.
There are expansions outside
of
these regions, though some are series expansions involving negative powers
of
z -
zoo
We now present the Cauchy Integral Formula.
Theorem:
Letf(z)
be analytic in
Iz
-
zol
< p and let C be the boundary
(circle)
of
this disk. Then,
z =
_1
rf
fez)
dz
f(
0)
2ni
':1c
z-zo
In
order to prove this,
we
first make use
of
the analyticity
off(z).
We
insert the power series expansion
off(z)
about
zO
into the integrand.
Then
we
have
fez)
2
[~
n]
--
=
--
L..Jcn(z-ZO)
Z-Zo
Z-Zo
n=O
Co
=
--+CO
+c2(z-zO)+···
Z-Zo'
v '
analytic function
As noted the integrand can be written as
fez)
=~+h(z)
Z-Zo
z-zo
'

Complex
Representations
of Functions
171
where h(z)
is
an
analytic function, since it
is
representable as a Taylor series
expansion
about
zoo
We have already shown
that
analytic functions are
differentiable, so by Cauchy's Theorem
4c
h(z)dz
=
O.
Noting also
that
Co
= J(zo)
is
the first term
of
a Taylor series expansion about z =
zo'
we have
<!
fez)
dz
=
~
[~+h(Z)]dZ=f(zo)cf
_l_dz
c z -
Zo
c z -
Zo
c z -
Zo
We need only compute the integral
<!c-
1
_
dz
to finish the
proof
of
z-zo
Cauchy's Integral Formula. This
is
done by parametrizing the circle,
Iz
-
zol
=
p.
Let
z -
Zo
= peiS.
(Note
that
this has the right complex modulus since
leiSI
=
1).
Then
dz =
ipeiSde.
Using this parametrization, we have
q
fez)
dz =
r27t
i
p
e
iS
.d8 = i
r27t
de
=
21ti
c z -
Zo
.b
pe'S
.b
iy
c
s x
Fig. Circular Contour
used
in
Proving
the
Cauchy Integral Formula
Therefore,
q
fez)
1 1
--dz
=
J(zo)
--dz
= 21tf(zo)
c
Z-Zo
Z-Zo
as was
to
be shown.
Example:
Using the Cauchy Integral
Formula
rf cosz
We now compute
'Ji11-4
2 6 5
dz.
z-
z -
z+
In
order
to
apply the Cauchy Integral Formula,
we
need
to
factor the
denominator,
z2
-
6z
+ 5 =
(z
-
1)
(z
-
5).
We next locate the zeroes
of
the
denominator. We see the contour and the points z
= I
and
z =
5.
The
only
point inside the region bounded by the contour
is
z =
l.
Therefore,
we
cosz
can apply the Cauchy Integral Formula for
J(z) =
--
to
the integral
z-5
