Brewster H.D. Mathematical Physics
Подождите немного. Документ загружается.

222
Transform
Techniques
in
Physics
APPLICATIONS
OF
THE
CONVOLUTION
THEOREM
There are many applications
of
the convolution operation.
In
this section
we
will describe a few
of
the applications.
The first application
is
filtering signals. For a given signal there might
be
some noise
in
the signal, some undesirable high frequencies, or the device
used for recording an analog signal might naturally not
be
able to record
high frequencies.
Let
f (t) denote the amplitude
of
a given analog signal and J
(co)
be
the Fourier transform
of
this signal.
Recall that the Fourier transform gives the frequency content
of
the
signal and that
co
=
27tv,
where v
is
the frequency in Hertz, or cycles per
second (cps).
There are many ways to filter out unwanted frequencies. The simplest
would be to just drop all
of
the high frequencies,
lcol
>
COo
for some cutoff
frequency
coo'
The Fourier transform
of
the filtered signal would then be zero for
lcol
>
coo'
This could be accomplished by multiplying the Fourier
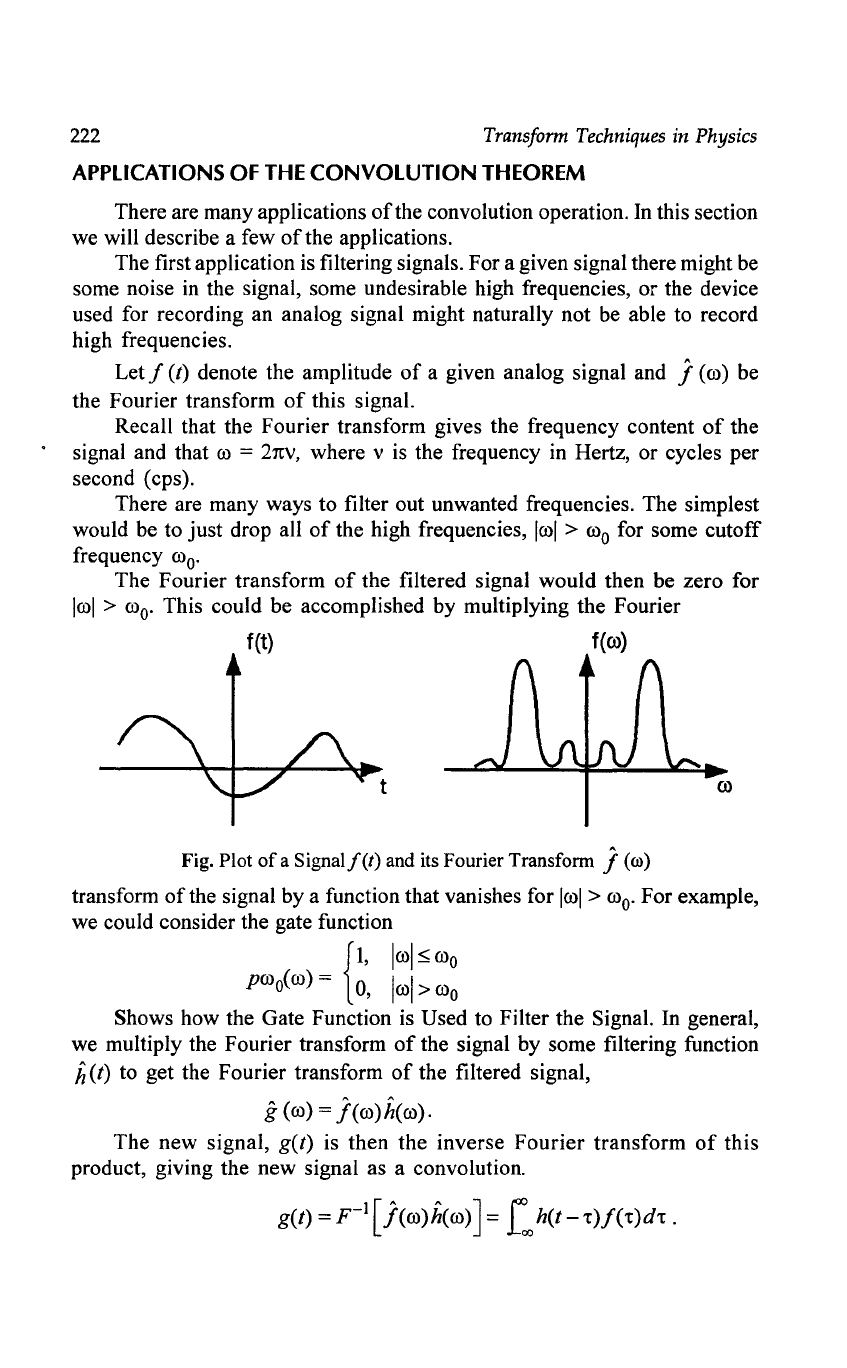
f(t)
f(ro)
t
ro
Fig. Plot
of
a
Signalf(t)
and its Fourier Transform J
(m)
transform
of
the signal by a function that vanishes for
lcol
>
coo'
For example,
we
could consider the gate function
{
I,
lcol
~
COo
pco
o
(
co)
= 0,
lcol
>
COo
Shows how the Gate Function
is
Used to Filter the Signal. In general,
we
multiply the Fourier transform
of
the signal by some filtering function
h(t)
to get the Fourier transform
of
the filtered signal,
g
(co)
=
J(co)h(co).
The new signal, g(t) is then the inverse Fourier transform
of
this
product, giving the new signal as a convolution.
get) =
F-
1
[J(co)h(co)
] =
[00
h(t -
t)f(t)dt
.

Transform
Techniques
in
Physics
223
Such processes occur often in systems theory as well. One thinks
off(t)
as the input signal into some filtering device which in turn produces the output,
g(t). The function h(t) is called the impulse response. This is because it is a
response to the impulse function,
&(t). In this case, one has
[00
h(t -
.)
&(.)
d.
= h(t)
Another application
of
the convolution
is
in
windowing. This represents
what happens when one measures a real signal. Real signals cannot be
recorded for all values
of
time. Instead data
is
collected over a finite time
A
f(oo)
(a)
•
-0>0
00
(b)
Fig. (a) Plot
of
the Fourier transform j
(00)
of
a signal. (b) The gatefunction
ProO
(00)
used to filter out high frequencies.
9(00)
(
(c)
Fig. (c) The product
of
the functions, g
(00)
= j
(oo)ProO
(00),
in (a) and (b)
interval.
If
the length
oftime
the data
is
collected
is
T, then the resulting signal
is zero outside this time interval. This can be modeled in the same way as

224
Transform
Techniques
in
Physics
with filtering, except the new signal will be the product
of
the old signal with
the windowing function.
The resulting Fourier transform
of
the new signal will be a convolution
of
the Fourier transforms
of
the original signal and the windowing function.
We can also use the convolution theorem to derive Parseval's Equality.
Llf(t)1
2
dt =
2~
Lli(ro)1
2
dro
This equality has a physical meaning for signals. The integral on the left
side is a measure
of
the energy content
of
the signal in the time domain.
The right side provides a measure
of
the energy content
of
the transform
of
the signal. Parseval's equality, sometimes referred as Plancherel's formula,
is simply a statement that the energy is invariant under the transform.
Let's rewrite the Convolution Theorem in the form
F-l
[i(k)g(k)]
=
if
* g)(t).
Then, by the definition
of
the inverse Fourier transform, we have
Setting t =
0,
Lf(t-u)g(u)du
=
;1t
Ci(ro)g(ro)dro.
Now, let get) =
f(-t)
,
orf;(-t)
=
g(-t).
Then, the Fourier transform
of
get) is related to the Fourier transform
off(t):
So, inserting this result into equation, we find that
Lf(-u)f(-u)du
=
2~
Cli(rof
dro
which implies Parseval's Equality.

Transform
Techniques
in
Physics
THE
LAPLACE
TRANSFORM
225
Up
until this point
we
have only explored Fourier exponential transforms
as one type
of
integral transform. The Fourier transform
is
useful on infinite
domains.
However, students are often introduced to another integral transform,
called the Laplace transform, in their introductory differential equations
class. These transforms are defined over semi-infinite domains and are
useful for solving ordinary differential equations. They also have proven
useful in engineering for solving circuit problems and doing systems
analysis.
The Laplace transform
of
a
function!
(t)
is
defined as
F
(s)
=
£W(s)
= r
!(t)e-stdt,
s >
o.
This
is
an improper integral and one needs
lim
!(t)e-
st
=
t-.oo
0
to guarantee convergence.
It
is
typical that one makes use
of
Laplace transforms by referring to a
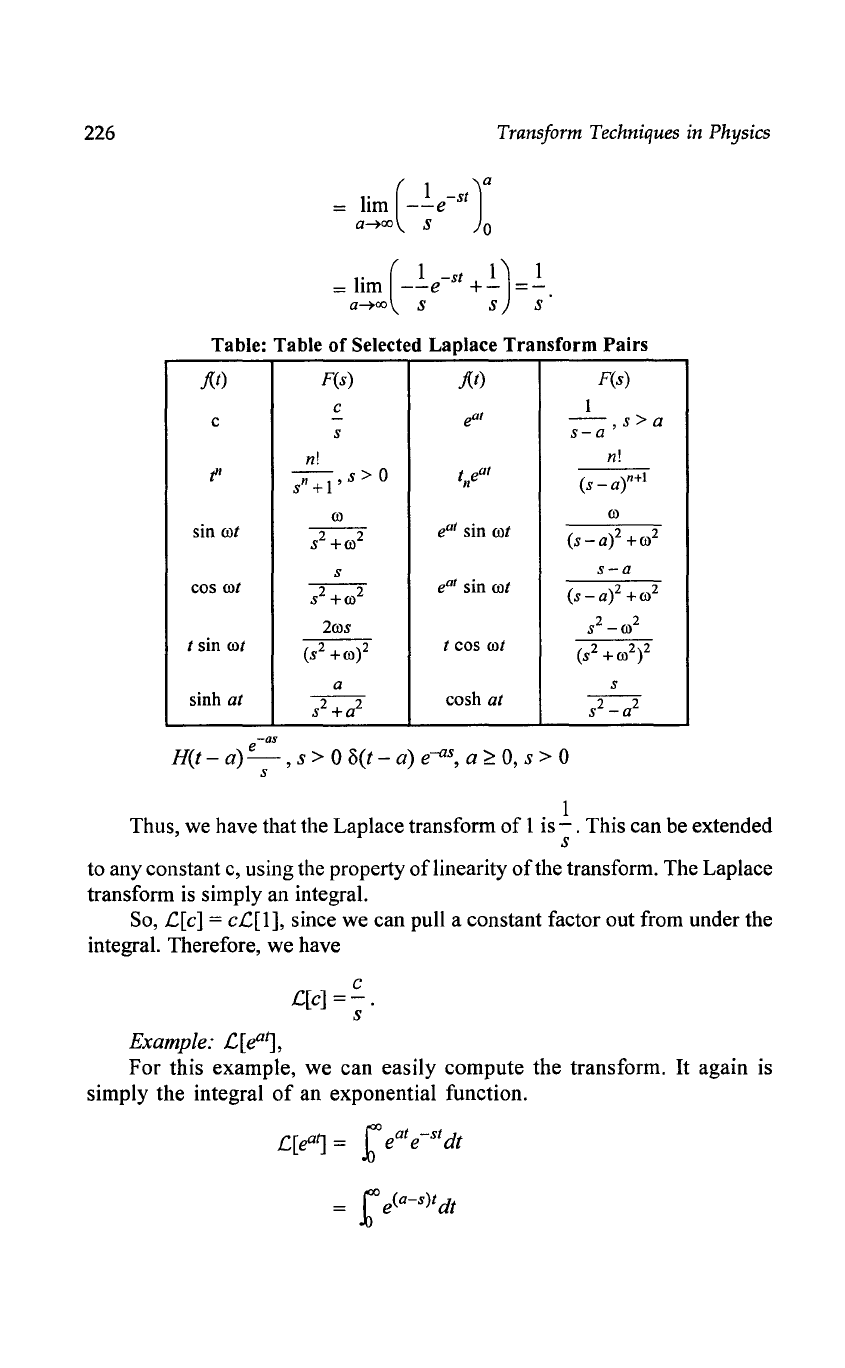
Table
of
transform pairs.
Combining
some
of
these
simple
Laplace
transforms
with
the
properties
of
the Laplace transform,
we
can deal with many applications
of
the Laplace transform. We will first prove a few
of
the given Laplace
transforms and show how they can be used to obtain new transform pairs.
In
the next section
we
will show how these can
be
used to solve ordinary
differential equations.
We
begin with some simple transforms. These are found by simply
using the definition
of
the Laplace transform.
Example: £[1]
For this example, we
insert!
(t) = 1 into our integral.
£[1]
= r e-stdt.
This is an improper integral and the computation is understood by
introducing an upper limit
of
a and then letting a
~
00.
We
will not always
write this limit, but it will be understood that this is how one computes
such improper integrals. Thus, we have
lim
re-stdt
a-.oo
226
Transform
Techniques
in
Physics
(
)
a
. 1 -st
= hm
--e
a~OCJ
S 0
Table: Table
of
Selected Laplace Transform Pairs
fit)
F(s)
fit)
F(s)
c
1
c
-
eat
--
s>a
s
s-a'
n!
n!
f'
~,s>O
t"e
al
(s-ar+!
s +
ro
ro
sin
rot
s2
+ro
2
eat
sin
rot
(s-a)2
+ro
2
s
s-a
cos
rot
s2
+ro
2
eat
sin
rot
(s -
a)2
+
ro
2
2ros
s2
_
ro
2
t sin
rot
(s2+ro)2
t
cos
rot
(s2
+
ro
2
)2
a
s
sinh
at
s2
+a
2
cosh
at
s2
_a
2
-as
e
H(t -
a)
- , S > 0
oct
-
a)
e-Gs,
a
~
0, S > 0
s
1
Thus, we have that the Laplace transform
of
1 is - . This can be extended
S
to any constant c, using the property
of
linearity
ofthe
transform. The Laplace
transform is simply an integral.
So,
L:[c]
= cL:[l], since we can pull a constant factor out from under the
integral. Therefore,
we
have
c
L:[c]
=
-.
S
Example:
L:[ea~,
For
this example,
we
can easily
compute
the
transform. It again is
simply the integral
of
an
exponential function.
L:[ea~
= r
eat
e-
st
dt
r e(a-s)tdt

Transform
Techniques
in
Physics
227
=
(_I_
e
<a-s)t)OO
a-s
0
=
lim
_1_
e
(a-s)t
__
1_=_1_
t~ooa-s
a-s
s-a
Note that
the
last limit was computed as limHooe(a-S)t =
O.
This is
only true
if
a
~-s
<
0,
or s >
a.
[Actually, a could
be
complex.
In
thIS
case
we would only need that s
is
greater than the real part
of
a.]
Example: £[cos at] and £[sin at]
In
these cases, we could again insert the functions directly into the
transform. For example,
£[cos at] = r
e-
st
cos
at
dt
.
Recall how one does such integrals involving both the trigonometric
function and the exponential function.
One integrates by parts two times and then obtains an integral
of
the form
with which one started. Rearranging the result the answer can be obtained.
However, there
is
a much simpler way to compute these transforms.
Recall that
e
iat
= cos
at
+ i sin at. Making use
of
the linearity
of
the
Laplace transform, we have
£[
eia~
=
£[
cos at] +
i£[
sin at].
Thus, transforming this complex exponential and looking at the real
and imaginary parts
of
the results will give both transforms at the same
time! The transform is simply computed as
£[eia~
=
reiate-Sldt=
re-(S-ia)tdt=-I_.-.
S-la
Note that
we
could easily have used the result for the transform
of
an
exponential, which was already proven.
In
this case s > Re(ia) =
O.
We now extract the real and imaginary parts
of
the result using the
complex conjugate
of
the denominator.
I I s
+ia
s + ia
--=----=
s - ia s - ia s + ia s2 + a
2
.
Reading
off
the real and imaginary parts gives
s
£[
cos at] = s2 +
a2
a
£[sin at] = 2 2 .
S
+a

228
Transform
Techniques
in
Physics
Example: £[t]
For this example
we
need to evaluate
£[t] =
.b
te -st dt .
This integration can be done using integration by parts. (Pick u = t
1 -st
and dv =
e-
st
dt.
Then, du = dt and v =
--e
.)
s
Example:
£[fl]
We can generalize the last example to powers greater than n =
1.
In
this case
we
have to
do
the integral
£[fl] =
.b
tne-stdt.
Following the previous example, we integrate by parts .
.btne-stdt
=
_tn~e-stl:
+n~
.bt-ne-stdt
=n~
.b
tne-stdt.
We
could continue to integrate by parts until the final integral can be
computed. However, look at the integral that resulted after one integration
by parts.
It
is
just the Laplace transform
of
tr
I
.
So, we can write the result
as
£[fl] =
~
£[tn-I] .
s
This
is
an example
of
an recursive definition
of
a sequence, in this
case a sequence
of
integrals. Denoting
In
= £[fl] =
.b
tne-stdt
1
and noting that I
[0]
= £[1]
=-,
we have the following.
s
n
1
I
-
-I
10
=-.
n -
n-I'
S S

Transform Techniques in Physics 229
This is also what is called a difference equation. It
is
a first order difference
equation with an initial condition",
1
0
.
There
is
a whole theory
of
difference
equations, which we will not get into here.
Our goal is to solve the above difference equation. It
is
easy to do by
simple iteration. Note that replacing n with
n -
1,
we have
n-l
I
n
_
1
=
--I
n
-
2
•
s
So, repeating the process we find
n
I =
-I
n
-
1
n s
n(n-l)
=
-;
-s-
I
n
-
2
n(n-l)
I
= 2
n-2.
S
We can repeat this process until we get to 1
0
,
which we know. In some
cases you need to be careful so that you can count the number
of
iterations
of
the process. So, we first ask what the result
is
after k steps. This can be seen
by watching for patterns. Continuing the iteration process, we have
n
In
=
-I
n
-
1
s
n(n-l)
I
= 2
n-2
S
=
n(n
-1)3(n - 2) I
n
-
3
s
n(n-I)(n-2)
...
(n-k+l)
I
= k n-k
s
Since we know 1
0
,
we
choose to stop at k = n obtaining
_
n(n-l)(n-2)
...
(2)(l) 1
=~
In
- n 0 n+l
S s
n!
Therefore, we have shown that £[(1] =
n+l.
[Such iterative techniques
s
are
useful
in
obtaining
a
variety
of of
integrals,
such
as
In
= L x
2n
e-
x2
dx.]

230
Transform
Techniques
in Physics
As a final note, one can extend this result to cases when n is not an integer.
To do this, one introduces what is called the Gamma function. This function
is defined as
r(x)=
.btX-le-tdt
Note the similarity to the Laplace transform
of
tx-
1
:
.cW-
1
]
=
.b
t
x
-
1
e -st
dt
.
For
x-I
an integer and s =
1,
we have that
rex)
= (x - I)!.
Thus,
the
Gamma
function
seems
to
be
a
generalization
of
the
factorial.
for values
of
p >
-I.
r(p+l)
.c[fP]
= sp+l
Example:
.c[
!].
We have to compute
Laplace Transform Properties
.c[aj{t) +
bg(t)]
=
aF
(s) + bG(s)
d
.c[t! (t)] = ds F(s)
"
[ddYt
]
I-J
= sY(s) -
yeO)
= s2y(s) - sy(O) -
y'
(0)
£[eQfJ(t)] = F (s - a)
L{H
(t
-
a)j
(t
- a)] =
e-QS
F(s)
L{(f*
g)(t)]
=
.c[f~!(t
- u)g(u) du] = F (s)G(s)
We can move the derivative
off
of
f by integrating by parts. This is similar
to what we had done when finding the Fourier transform
of
the derivative
of
a function.

Transform
Techniques
in
Physics
Thus letting u =
e-
st
and v =
/(t),
we have
£[d/]
=
~d/
e-stdt
dt
.b
dt
=
/(t)e-
st
\;
+s
r
/(t)e-stdt
=
-/(0)
+
sF(s).
231
Here we have assumed that}{t)e-
st
vanishes for large
t.
The final result
is
that
£[d/]
=
sF
(s) -
/(0)
dt
.
[
d
2
/]
Example: £
dt
2
•
We can compute this using two integrations by parts, or we could
make use
of
the last result.
d/(t)
Letting g(t)
=~
, we have
But,
So,
£[d
2
{]
=£[dg]=SG(S)-g(O)=SG(S)-
/'(0)
m m .
G(s) =
£[
r]
=
sF(s)
-
/(0).
[
d
2
/]
£
dP
= sG(s) - f (0)
=
s(sF
(s)
-/(0)
- f (0)
= s2F (s)
-·s/(O)
- f (0).
SOLUTION
OF
ODES
USING
LAPLACE
TRANSFORMS
One
of
the typical applications
of
Laplace transforms
is
the solution
of
nonhomogeneous linear constant coefficient differential equations. In the
following examples we will show how this works.
The general idea
is
that one transforms the equation for an unknown
