Brewster H.D. Mathematical Physics
Подождите немного. Документ загружается.


22
Mathematical
Basics
new
tensor. Thus the product
of
a scalar and a tensor
of
second order forms a
tensor
of
second order, where each element results from the initial tensor
of
second order by scalar multiplication:
{
a
.
alIa
.
a12
a
.a
13
}
a·
{aij} =
{a
·aij} = a
·a2la
'a22a
'a23
a
·a3Ia·
a32a·a33
The outer product
of
a vector (tensor
of
I st order) and a tensor
of
2nd
order results in a tensor
of
3rd order with altogether 27 elements. The inner
product
of
tensors, however, can result in a contraction
of
the order. As
examples are cited the products
aij
.
bi
{aij
}.
{b
j}
= {:::
:::
:::}{:~}
=
{:~:::
::::~:
::~:::}
a3]
a32
a33
b
3
a3]b]
+
a32
b
2
+
a33
b
3
and
in summary this can be written as:
{aij}'
{b
j
}
= {(aijb
j
)}
=
{(ab)j}
respectively.
{b
j
}·
{aij} = {(biaij)} =
{(ab)j}
If
one takes into account the above product laws
The multiplication
of
a tensor
of
second order by the unit tensor
of
second
order,
i.e.
the
'Kronecker
Delta',
yields
the
initial
tensor
of
second order
{8ij}.{aij}={~
~
~}.{:::
:::
:::}={aij}
o 0 I
a31
a32 a33
Further products can be formulated, as for example cross products between
vectors and tensors
of
second order
{a/}
.
{b
jk
}
=Eikl
·a
i
·b
Jk
but these are not
of
special importance for the laws
in
fluid mechanics.
Mathematical
Basics
23-
FIELD
VARIABLES
AND
MATHEMATICAL
OPERATIONS
In
fluid mechanics it is usual to present thermodynamic state quantities
of
fluids, like density, pressure P, temperature T, internal energy e etc as a
function
of
space and time, a Cartesian coordinate system being applied here
generally.
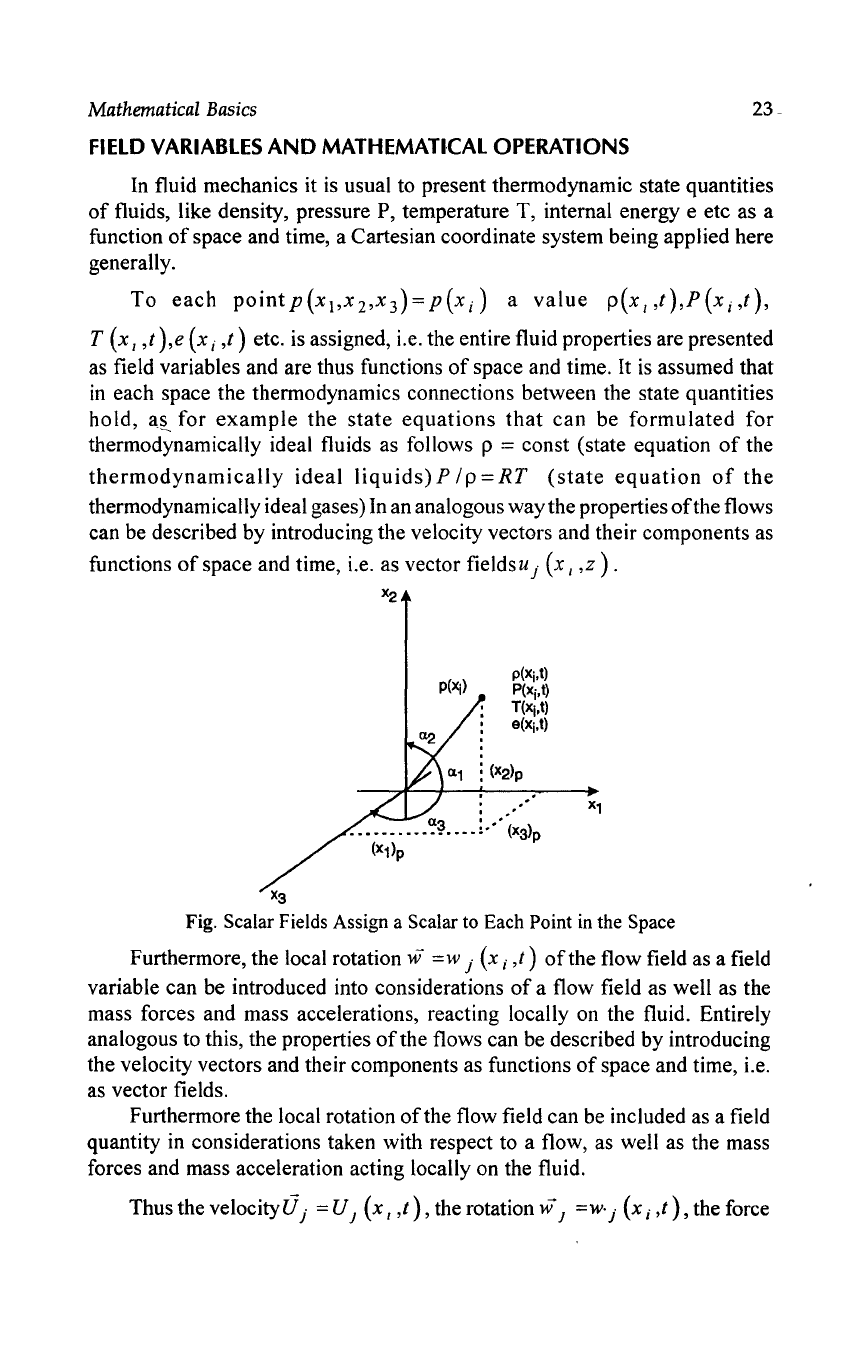
To
each
pointp(xl>x2,x3)=p(x;)
a
value
p(Xl't),p(x;,t),
T
(x
I ,t
),e
(x;
,t) etc. is assigned, i.e. the entire fluid properties are presented
as field variables and are thus functions
of
space and time. It is assumed that
in
each space the thermodynamics connections between the state quantities
hold,
a~
for
example
the
state
equations
that
can
be
formulated
for
thermodynamically ideal fluids as follows p = const (state equation
of
the
thermodynamically
ideal
liquids)P
/p=RT
(state
equation
of
the
thermodynamically ideal gases) In an analogous way the properties
of
the flows
can be described by introducing the velocity vectors and their components as
functions
of
space and time, i.e. as vector fieldsu j
(x
I ,z ).
X3
X2
p(Xj,t)
P(Xj,t)
T(xI.t)
e(xj,t)
.
--
/~~-u3
:
•.
, .
••••••••••••••••
!-
(x3)p
(x1)p
Fig. Scalar Fields Assign a Scalar to Each Point
in
the Space
Furthermore, the local rotation W
=w
j
(x
i ,I)
of
the flow field as a field
variable can be introduced into considerations
of
a flow field as well as the
mass forces and mass accelerations, reacting locally on the fluid. Entirely
analogous to this, the properties
of
the flows can be described by introducing
the velocity vectors and their components as functions
of
space and time, i.e.
as vector fields.
Furthermore the local rotation
of
the flow field can be included as a field
quantity in considerations taken with respect to a flow, as well as the mass
forces and mass acceleration acting locally on the fluid.
Thus the velocity
OJ
= U
J
(x
I ,I) , the rotation w
J
=w-
j
(x
i ,I) , the force

24
Mathematical
Basics
K
j
=Kj(xl't)
and
the
acceleration
gj(x"t)
can be stated as field
quantities and be employed as such quantities
in
the following considerations.
Analogously tensors
of
second and higher order can also be introduced
as field variables.
For example
tlj
(x,
,f) which
is
the molecule caused momentum transport
existing
in
the space i.e. at the point p (x,) at time t for the velocity
components
U
j
acting
in
the direction.
Further represents the fluid-element deformation depending on the
gradients
of
the velocity field at the location p (x,) at the time
t.
Fig. Vector Fields Assign a vector to Each Point
in
the Space.
The properties introduced as field variables into the above presentations
of
tensors
of
zero order (scalars), tensors
of
first order (vectors) and tensors
of
second order are employed
in
fluid mechanics to describe the fluid flows
and usually attributed to Euler (1707-1783).
In
this description all quantities
considered
in
the presentations
of
fluid-mechanics are dealt as functions
of
space and time.
Mathematical
operations
like
addition,
subtraction,
division,
multiplication, differentiation, integration etc. that are applied to these
quantities, are subject to the known laws
of
mathematics. For the differentiation
of
a scalar fields, for example density p, gives:
In the last term, the summation symbol
I~=I
was omitted and the

Mathematical
Basics
25
"Einstein's summation convention" was employed, according to which the
double index
i:
in
(
::4
)(
~/)
prescribes a summation over three terms
i =1,2,3 i.e.,
t(::.)(
d;/
)=
::.
d;/
,=!
1 1
The differentiation
of
vectors yield
is
given by the following expressions:
- T
dU
_{dU!
dU
2
dU
3
}
--
--,--,--
dt dt dt dt
dU
I
::::::>--
dt '
i = 1,2,3
i.e. each component
of
the vector
is
included
in
the differentiation. As the
considered velocity vector depends
on
space xi and the time t, the following
differentiation law holds:
dU·
au·
au
.
(dX
)
__
1 =
__
1 +
__
1
__
I
dt at ax i dt
When one applies the Nabla operator (or) Del operator
v-{
a a
a}T
_{
a }
-
aXJ'Ox2'0x3
-
aXi
'
i = 1,2,3
on a scalar field quantity a vector results
vo.={ao.,
au
,
ao.}T
=grado.={
ao.},
ax!
aX2
Ox3
ax;
i = 1,2,3
This shows that the Nabla or Del operator
V results in a vector field, the
gradient field. The different components
of
the resulting vector are formed
from the prevailing partial derivations
of
the scalar field
in
the directions xi.
The scalar product
of
the
V'
operator with a vector yields scalar variables:
n -
ao.!
ao.2
ao.3
_ d'
ao.
l
V'o.=-+--+---
IVo.=--
ax!
aX2
aX3
aXi
Here in
ao.;
/
ax
i the double index i indicates again the summation over
all three terms, i.e.
~ao.;
ao.,
~
-a
::::::>
-a
(Einstein's summation convention)
i
=!
'X
i
'X
i
The
vector
product
of
the
V'
operator
with
the
vector
a.
:
yields
correspondingly:

26
Mathematical
Basics
-oa
2
10X
3
}
-oa
3
lox
I = rot a
-oallox2
or
;Ola
oa·
n - - U 1 }
v
xa=rota=-E1jk
--ek
=E1jk
--ek
ox}
oX
l
the Levi-Civita symbol called alternating unit tensor E ijk
is
defined
as
follows:
{
o:
i~
two
of
the
tl~~ee
indices are equal
Eijk=
+1:lf
ljk
=123,2310r312
-1:if
ijk =132,213or321
Concerning
the
above-mentioned products
of
the
V
operator
the
distributive law holds,
but
not
the commutative and associative laws.
If
one
applies the
V operator to the gradient field
of
a scalar function, the Laplace
operator
V2
(alternative way
of
notation V),that when applied to a can be
written as follows:
2 o
2
a o
2
a o
2
a 0
2
Va=(V·V)a=-+-+-=---
Oxf
ox?
oxf
Oxioxi
The
Laplace
operator
can also
be
applied
to
vector fields
of
the
components.
FUNCTIONAL
ANALYSIS
METRIC
SPACES
Definition: A metric space
is
a set X
and
a mapping
d:
XX
X
~
R, called
a metric, which satisfies:
d(x,y)~O
•
d(x,y)
= 0 ¢:>x = Y
•
d(x,y)
= d(y,
x)
•
d(x,y)~d(x,z)+d(z,y)
Definition:
A
sequence{xn}~=I'
of
elements
of
a
metric space
(X; d)
is
said
to
converge to an element x E X if d(x; xn)
~
o.

Mathematical
Basics
27
Definition:
Let
(X, d)
be
a metric space.
•
The
set B (y,
r)
=
{x
E
XI
d(x.
y)
<
r}
is
called
the
open
ball
of
radius
r
about
y;
the
set B (y,
r)
=
{x
E
Xl
d(x,
y)
~
rl
is
calle
the
closed ball
of
radius r
about
y;
the
set S (y,
r)
=
Ix
E
Xl
d(x,
y)
=
r}
is
called
the
sphere
of
radius r
about
y;
• A set 0 c X
is
called
open
if
\I)' E 0 3r >
0:
B
(r,
r)
~
0;
A set N c X is called a
neighborhood
of
YEN
if3r
>
0:
B(y, r) E
N;
Apointx
E Xis a limit point
ofa
setE
cXif\lr
>
0:
B
(x;
r)
n(EI{x})
= 0 ,i.e. if E contains points other
than
x arbitrarily close
to
x;
• A set
Fe
X is called closed
if
F
contains
all its limit
points;
• x E G
~
X is called
an
interior
point
of
G
if
G
is
a
neighborhood
ofx.
•
The
intersection S
of
all closed sets
containing
S
~
X is called
the
closure
of
S.
The
closure
of
S
~
X is
the
smallest set containg S.
The
interior
of
S,
SO,
is
the
set
of
interior points.
It
is
the
largest
open
set contained in S.
•
The
boundary
of
S
is
the
set
as
=
S\so.
Theorem:
Let (X, d)
be
a metric space.
• A set 0 is
open
iff
X\O is closed
•
xn
~
x
iff
\I
neighborhood
N
of
x
3m:
n
~
m implies
xn
E N;
•
The
set
of
interior
points
of
a set is open;
•
The
union
of
a set
and
all its limit
points
is closed;
• A set is
open
iff
it is a
neighborhood
of
each
of
its points.
The
union
of
any
number
of
open
sets is open.
The
intersection
of
finite
number
of
open
sets
is
open.
The
union
of
finite
number
of
closed sets is closed.
The
intersection
of
any
number
of
closed sets
is
closed.
•
The
empty
set
and
the
whole space
are
both
open
and
closed.
Theorem: A subset S
of
a metric space X is closed
iff
every convergent
sequence in
S has its limit in
S,
i.e.
{xn}:=l'
xn
ES,X
n
~x
=>
XES
Theorem:
The
closure
of
a subset S
of
a metric space X
is
the
set
of
limits
of
all convergent sequences in S,i.e.
S =
{x
E
Xl
3x
n E
S:
X n
~
x}
.
Definition: A subset, Y c X,
of
a metric space (X, d) is called dense
if
Theorem:
Let
S
be
a
subset
in a metric space X.
Then
the
following
conditions are equivalent:
• S
is
dense in X,

28 Mathematical Basics
· s
=X,
Every non-empty subset
of
X contains an element
of
S.
Definition: A metric
spaceXis
called separable
if
it has a countable dense
set.
Definition: A subset
SeX
of
a metric space X
is
called compact
if
every
sequence
{x
n
}
in
S contains a convergent subsequence whose limit belongs to
S.
Theorem: Compact sets are closed and bounded.
Definition:
A
sequence
{xnC=1 '
of
elements
of
a
metric
space
(X, d) is
called
a
Cauchy
sequence
if
VE
> 0 3N:
11;
m
~
N
implies
d(xn' x,,) < E .
Proposition: Any convergent sequence
is
Cauchy.
Definition: A metric space
in
which all Cauchy sequences converge
is
called complete.
Definition: A
mapping!
X
---?
Y from a metric space (X, d) to a
::;
metric
space
(Y; p)
is
called continuous at x
iff(xn)
~
(x)
\:I
{xn}~=I'
xn
E
~
x, i.e. the image
of
a convergent sequence converges to the
image
of
the limit.
Definition: A bijection (one-to-one onto mapping)
h:
X
---?
Y from (X, d)
to
(Y, p)
is
called isometry
if
it preserves the metric, i.e.
p(h(x), hey)) = d(x,
y)
\:Ix;
y E X
Proposition: Any isometry is continuous.
Theorem:
If
(X, d)
is
an incomplete metric space, it
is
possible
to::;
nd a
complete metric space
(X,
d)
so that X
is
isometric to a dense subset
of
X .
VECTOR
SPACES
Definition: A complex vector space is a nonempty set V with
two
operations:
+:
V x V
---?
Vand
.:
c::;
V
---?
V that satisfy the following conditions:
•
•
•
•
•
•
•
VX,y,ZE
V
x+y=y+x
(x +
y)
+ Z = x + (y + z)
30E
V:
Vx
E
V:
x + 0 = X
VXE
V3(-x)2V:x+(-x)=O
Va,
~
E C, Vx, Y E V
a(~x)
=
(a~)x
(a
+
P>x
=
ax
+
~x
a(x
+
y)
= ax +
ay

Mathematical
Basics
29
•
1·x=x
A real vector space is defined similarly.
Examples: (Function Spaces). Let Q c
ffi.n
be an open subset offfi.
n
.
•
P(Q)
is the space
of
all polynomials
of
n variables as functioJ1s
on
Q.
•
qQ)
is the space
of
all continuous complex valued functions
on
Q.
• Ck(Q)
is
the space
of
all complex valued functions with continuous
partial derivatives
of
order k on Q.
•
COO(Q)
is the space
of
all infinitely differentiable
complex
valued
(smooth) functions on
Q.
Example: (Sequence Spaces (lP-Spaces)). Let p
~
1.
IP
is the space
of
all
1
00
(~
pJp
infinite sequences f
zn
}n=1
of
complex numbers such that
~Iznl
<
00.
Definition: Let
Vbe
a complex vector space and letxI, ... x
k
E Vand
(XI'
.•. '
(Xk
E C. A vector x =
(Xlxl
+ ...
(X0k
is called a linear combination
of
xI'··· x
k
.
Definition: A finite
collection
of
vectors
x
1'
...
' x
k
is
called
linearly
independent
if
k
L(XiXi
= 0
<=>
(Xi
=
0,
i = 1,2,
...
,
k.
i=1
An arbitrary colection
of
vectors B =
{xn}
:=1
is
called linearly independent
if
every finite subcollection is linearly independent. A collection
of
vectors
which is not linearly independent is called linearly dependent.
Definition: Let B c V be a subset
of
a vector space
V.
Then span B is the
set
of
all finite linear combinations
of
vectors from B
Proposition:
Let
B c V be a subset
of
a vector space
V.
Then span B
is
a
subspace
of
V.
Definition: A set
of
vectors B c V is called a basis
of
V (or a base
of
V)
if
B is linearly independent and span B =
V.
If:3 a finite basis in
V,
then V is
called
finite
dimensional
vector
space.
Otherwise
V is
called
in
finite
dimensional
vector
space.
Proposition:
The
number
of
vectors in
any
basis
of
a finite dimensional
vector space is the same.

I
30
Mathematical
Basics
Definition: The number
of
vectors
in
a basis
of
a finite dimensional vector
space
is
called the dimension
of
V,
denoted by dim
V.
NORMED
LINEAR
SPACES
Definition:
A
normed
linear
space
is a
vector
space,
V,
over
e
(or R) and a mapping
II
.
II:
V
~
R,
called a norm, that satisfies:
•
Ilvll
~
0
\fv
E V
•
Ilvll=O<=>v=O
•
lIavll
=
1$lllvll
\fvE
V,
\fa
E e
•
Ilv
+
wll
$llvll +
Ilwll
\fv,wE
V
Examples:
• Norms
in
IRn:
n
Ilxll
l
=
2:
Ix;
I
;=1
• A norm
in
en
1
Ilzll
~
(~lz'12
J'
• Let n
IRn
be a closed bounded subset ofIRn and
dx
=
dx
l
...
dXn
be
a measure
in
IRn.
Norms
in
C(Q) can be defined by
l!flloo
=
!~~lf(x)1
1
l!fllp
=
(1If(x)IP
dX)P
Ilf
Ih
=
blf(x)ldx
• A norm in
IP

Mathematical
Basics
31
• A norm in r
Proposition:
A
normed
linear
space
(V,
II
.
II)
is a
metric
space
(V, d) with the induced metric d(v, w) =
IIv
-
wll·
Convergence,
open
and
closed
sets,
compact
sets,
dense
sets,
completeness,
in
a normed linear space are defined as in a metric space in the
induced metric.
Definition: A normed linear space
is
complete
if
it
is
complete as a metric
space
in
the induced metric.
Definition: A complete nonned linear space
is
called the Banach space.
Definition: A bounded linear transformation from a normed linear space
(V,
11·ll
r
.)
to a normed linear space (W,
11·ll
w
)
is
a mapping
T:
V
~
Wthat satisfies:
• T(av +
~w)
=-=
aT(v)
+
~T(w),
"iv, WE
V,
"ia,~
E C,
IIT(v)llr~
Cjlvll
w
for some C
~
0.
• The number
_ sup
II
T(v)
Ilw
liT
11-
VEVV;tO
II
v
Ilv
is called the norm
of
T.
Theorem: Any bounded linear tranformation between two normed linear
spaces
is
continuous.
Theorem: A bounded linear transformation,
T:
V
~
W,
from a normed
linear
space
(V,
II
.
Ilv)
to
a
complete
normed
linear
space
(W,
II
.
IIrv)
can be uniquely extended to a bounded linear transformation,
T,
from the completion
Vof
V to
(W,
II
~
lin,).
The extension
of
T preserves the
norm
11111
=
11111·
NOTES
ON
LEBESGUE
INTEGRAL
Definition:
Characteristic
function
of
a
set
A c X is a
mapping
XA:
X
~
{O,
I}
defined by
{
I,
XA(x)
=
0,
if
XE
A
if
x
rt
A
Definition: For a non-zero
function!
]R1l
~]R,
the set, suppf,
of
all points
x
E
]R1l
for
whichf(x)
*-
° is called the support
off,
i.e.
suppf=
{x
E ]Rlllf(x)
*-
O}.
Clearly,
sUPP
XA
= A.
Definition: Let I be a semi-open interval
in
]Rn
defined by
