Brennen Ch.E. Fundamentals of Multiphase Flow

Подождите немного. Документ загружается.

quently collapse as they are convected into regions of higher pressure within

the blade passages of the pump. The displacement of liquid by this volume

growth and collapse introduces an additional ﬂow area restriction into the

ﬂow, an additional inlet nozzle caused by the cavitation. Stripling and Acosta

(1962) and others have suggested that the head degradation due to cavita-

tion could be due to a lack of pressure recovery in this eﬀective additional

nozzle.

219

HOMOGENEOUS FLOWS

9.1 INTRODUCTION

In this chapter we shall be concerned with the dynamics of multiphase ﬂows

in which the relative motion between the phases can be neglected. It is clear

that two diﬀerent streams can readily travel at diﬀerent velocities, and in-

deed such relative motion is an implicit part of the study of separated ﬂows.

On the other hand, it is clear from the results of section 2.4.2 that any two

phases could, in theory, be suﬃciently well mixed and therefore the disperse

particle size suﬃciently small so as to eliminate any signiﬁcant relative mo-

tion. Thus the asymptotic limit of truly homogeneous ﬂow precludes relative

motion. Indeed, the term homogeneous ﬂow is sometimes used to denote a

ﬂow with negligible relative motion. Many bubbly or mist ﬂows come close

to this limit and can, to a ﬁrst approximation, be considered to be homoge-

neous. In the present chapter some of the properties of homogeneous ﬂows

will be considered.

9.2 EQUATIONS OF HOMOGENEOUS FLOW

In the absence of relative motion the governing mass and momentum conser-

vation equations for inviscid, homogeneous ﬂow reduce to the single-phase

form,

∂ρ

∂t

∂

∂x

(ρu

) = 0 (9.1)



∂u

∂t

+ u

∂u

∂x



= −

∂p

∂x

+ ρg

(9.2)

220

where, as before, ρ is the mixture density given by equation 1.8. As in single-

phase ﬂows the existence of a barotropic relation, p = f(ρ), would complete

the system of equations. In some multiphase ﬂows it is possible to establish

such a barotropic relation, and this allows one to anticipate (with, perhaps,

some minor modiﬁcation) that the entire spectrum of phenomena observed in

single-phase gas dynamics can be expected in such a two-phase ﬂow. In this

chapter we shall not dwell on this established body of literature. Rather,

attention will be conﬁned to the identiﬁcation of a barotropic relation (if

any) and focused on some ﬂows in which there are major departures from

the conventional gas dynamic behavior.

From a thermodynamic point of view the existence of a barotropic relation,

p = f(ρ), and its associated sonic speed,

c =



dρ



(9.3)

implies that some thermodynamic property is considered to be held constant.

In single-phase gas dynamics this quantity is usually the entropy or, occa-

sionally, the temperature. In multiphase ﬂows the alternatives are neither

simple nor obvious. In single-phase gas dynamics it is commonly assumed

that the gas is in thermodynamic equilibrium at all times. In multiphase

ﬂows it is usually the case that the two phases are not in thermodynamic

equilibrium with each other. These are some of the questions that must be

addressed in considering an appropriate homogeneous ﬂow model for a mul-

tiphase ﬂow. We begin in the next section by considering the sonic speed of

a two-phase or two-component mixture.

9.3 SONIC SPEED

9.3.1 Basic analysis

Consider an inﬁnitesimal volume of a mixture consisting of a disperse phase

denoted by the subscript A and a continuous phase denoted by the subscript

B. For convenience assume the initial volume to be unity. Denote the initial

densities by ρ

and ρ

and the initial pressure in the continuous phase

by p

. Surface tension, S, can be included by denoting the radius of the

disperse phase particles by R. Then the initial pressure in the disperse phase

is p

= p

+2S/R.

Now consider that the pressure, p

, is changed to p

+ δp

where the

diﬀerence δp

is inﬁnitesimal. Any dynamics associated with the resulting

ﬂuid motions will be ignored for the moment. It is assumed that a new equi-

221

librium state is achieved and that, in the process, a mass, δm, is transferred

from the continuous to the disperse phase. It follows that the new disperse

and continuous phase masses are ρ

+ δm and ρ

− δm respectively

where, of course, α

=1− α

. Hence the new disperse and continuous phase

volumes are respectively

(ρ

+ δm)/



∂ρ

∂p



δp



(9.4)

and

(ρ

− δm)/



∂ρ

∂p



δp



(9.5)

where the thermodynamic constraints QA and QB are, as yet, unspeciﬁed.

Adding these together and subtracting unity, one obtains the change in total

volume, δV , and hence the sonic velocity, c,as

−2

= −ρ

δV

δp



δp

→0

(9.6)

−2

= ρ



∂ρ

∂p



δp

∂ρ

∂p



−

(ρ

− ρ

)

δm

δp



(9.7)

If it is assumed that no disperse particles are created or destroyed, then the

ratio δp

/δp

may be determined by evaluating the new disperse particle

size R + δR commensurate with the new disperse phase volume and using

the relation δp

= δp

−

δR:

δp



1 −

3α

δm

δp





1 −

3ρ

∂ρ

∂p





(9.8)

Substituting this into equation 9.7 and using, for convenience, the notation

∂ρ

∂p



;

∂ρ

∂p



(9.9)

the result can be written as

ρc



−

δm

δp



−

3ρ





1 −

3ρ



(9.10)

This expression for the sonic speed, c, is incomplete in several respects.

First, appropriate thermodynamic constraints QA and QB must be identi-

ﬁed. Second, some additional constraint is necessary to establish the rela-

tion δm/δp

. But before entering into a discussion of appropriate practical

222

choices for these constraints (see section 9.3.3) several simpler versions of

equation 9.10 should be identiﬁed.

First, in the absence of any exchange of mass between the components

the result 9.10 reduces to

ρc



1 −

3ρ



(9.11)

In most practical circumstances the surface tension eﬀect can be neglected

since S  ρ

R;thenequation9.11becomes

= {ρ

+ ρ

}





(9.12)

In other words, the acoustic impedance for the mixture, namely 1/ρc

,is

simply given by the average of the acoustic impedance of the components

weighted according to their volume fractions. Another popular way of ex-

pressing equation 9.12 is to recognize that ρc

is the eﬀective bulk modulus

of the mixture and that the inverse of this eﬀective bulk modulus is equal

to an average of the inverse bulk moduli of the components (1/ρ

and

1/ρ

) weighted according to their volume fractions.

Some typical experimental and theoretical data obtained by Hampton

(1967), Urick (1948) and Atkinson and Kyt¨omaa (1992) is presented in ﬁgure

9.1. Each set is for a diﬀerent ratio of the particle size (radius, R)tothe

wavelength of the sound (given by the inverse of the wavenumber, κ). Clearly

the theory described above assumes a continuum and is therefore relevant

to the limit κR → 0. The data in the ﬁgure shows good agreement with

the theory in this low frequency limit. The changes that occur at higher

frequency (larger κR) will be discussed in the next section.

Perhaps the most dramatic eﬀects occur when one of the components is

a gas (subscript G), that is much more compressible than the other com-

ponent (a liquid or solid, subscript L). In the absence of surface tension

(p = p

= p

), according to equation 9.12, it matters not whether the gas is

the continuous or the disperse phase. Denoting α

by α for convenience and

assuming the gas is perfect and behaves polytropically according to ρ

∝ p,

equation 9.12 may be written as

=[ρ

(1 − α)+ρ

α]



(1 − α)



(9.13)

This is the familiar form for the sonic speed in a two-component gas/liquid or

gas/solid ﬂow. In many applications p/ρ

 1 and hence this expression

223

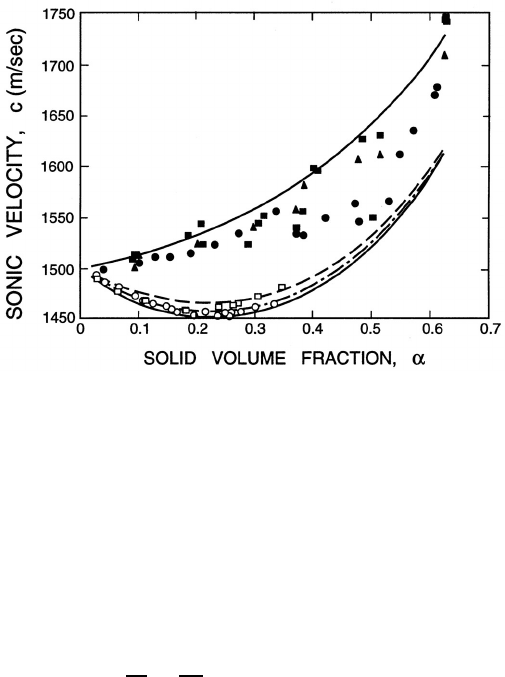
Figure 9.1. The sonic velocities for various suspensions of particles in

water: , frequency of 100kHz in a suspension of 1µm Kaolin particles

(Hampton 1967) (2κR =6.6 × 10

−5

); , frequency of 1MHz in a suspen-

sion of 0.5µm Kaolin particles (Urick 1948) (2κR =3.4 × 10

−4

); solid sym-

bols, frequencies of 100kHz − 1MHz in a suspension of 0.5mm silica parti-

cles (Atkinson and Kyt¨omaa 1992) (2κR =0.2 − 0.6). Lines are theoretical

predictions for 2κR =0, 6.6 × 10

−5

,3.4 × 10

−4

,and2κR =0.2 − 0.6in

ascending order (from Atkinson and Kyt¨omaa 1992).

may be further simpliﬁed to

[ρ

(1 − α)+ρ

α] (9.14)

Note however, that this approximation will not hold for small values of the

gas volume fraction α.

Equation 9.13 and its special properties were ﬁrst identiﬁed by Minnaert

(1933). It clearly exhibits one of the most remarkable features of the sonic

velocity of gas/liquid or gas/solid mixtures. The sonic velocity of the mix-

ture can be very much smaller than that of either of its constituents. This is

illustrated in ﬁgure 9.2 where the speed of sound, c, in an air/water bubbly

mixture is plotted against the air volume fraction, α. Results are shown for

both isothermal (k = 1) and adiabatic (k =1.4) bubble behavior using equa-

tion 9.13 or 9.14, the curves for these two equations being indistinguishable

on the scale of the ﬁgure. Note that sonic velocities as low as 20 m/s occur.

Also shown in ﬁgure 9.2 is experimental data of Karplus (1958) and Gouse

and Brown (1964). Data for frequencies of 1.0 kHz and 0.5 kHz are shown

in ﬁgure 9.2, as well as data extrapolated to zero frequency. The last should

224

Figure 9.2. The sonic velocity in a bubbly air/water mixture at atmo-

spheric pressure for k =1.0and1.4. Experimental data presented is from

Karplus (1958) and Gouse and Brown (1964) for frequencies of 1 kHz (),

0.5 kHz (), and extrapolated to zero frequency().

be compared with the low frequency analytical results presented here. Note

that the data corresponds to the isothermal theory, indicating that the heat

transfer between the bubbles and the liquid is suﬃcient to maintain the air

in the bubbles at roughly constant temperature.

Further discussion of the acoustic characteristics of dusty gases is pre-

sented later in section 11.4 where the eﬀects of relative motion between the

particles and the gas are included. Also, the acoustic characteristics of di-

lute bubbly mixtures are further discussed in section 10.3 where the dynamic

response of the bubbles are included in the analysis.

9.3.2 Sonic speeds at higher frequencies

Several phenomena can lead to dispersion, that is to say to an acoustic

velocity that is a function of frequency. Among these are the eﬀects of bubble

dynamics discussed in the next chapter. Another is the change that occurs at

higher frequencies as the wavelength is no longer eﬀectively inﬁnite relative

to the size of the particles. Some experimental data on the eﬀect of the

ratio of particle size to wavelength (or κR) was presented in ﬁgure 9.1.

Note that the minimum in the acoustic velocity at intermediate volume

fractions disappears at higher frequencies. Atkinson and Kyt¨omaa (1992)

225

Figure 9.3. An example of the dimensionless attenuation, ζR,atlowfre-

quencies as a function of solids fraction, α. The experimental data (◦)is

for a suspension of Kaolin particles in water with 2κR =3.4 × 10

−4

(Urick

1948); the theoretical line is from Atkinson and Kyt¨omaa (1992).

modeled the dynamics at non-zero values of κR using the following set of

governing equations: (a) continuity equations 1.21 for both the disperse and

continuous phases with no mass exchange (I

= 0) (b) momentum equations

1.45 for both phases with no gravity terms and no deviatoric stresses σ

Cki

0 and (c) a particle force, F

(see equation 1.55) that includes the forces

on each particle due to the pressure gradient in the continuous phase, the

added mass, the Stokes drag and the Basset memory terms (see section 2.3.4,

equation 2.67). They included a solids fraction dependence in the added

mass. The resulting dispersion relation yields sound speeds that depend on

frequency, ω, and Reynolds number, ρ

ωR

/µ

, but asymptote to constant

values at both high and low Reynolds numbers. Typical results are plotted

in ﬁgure 9.1 for various κR and exhibit fair agreement with the experimental

measurements.

Atkinson and Kyt¨omaa (1992) also compare measured and calculated

acoustic attenuation rates given non-dimensionally by ζR where the am-

plitude decays with distance, s, according to e

−ζs

. The attenuation results

from viscous eﬀects on the relative motion between the particles and the

continuous ﬂuid phase. At low frequencies the relative motion and therefore

the attenuation is dominated by contribution from the Stokes drag term in

equation 2.67; this term is proportional to ω

. Though the measured data on

attenuation is quite scattered, the theory yields values of the dimensionless

226

attenuation, ζR, that are roughly of the correct magnitude as shown by the

example in ﬁgure 9.3. On the other hand at high frequencies (large κR)the

theoretical attenuation is dominated by the Basset term and is proportional

to (µ

ω)

; it also increases nearly linearly with the solids fraction. However

the measured attenuation rates in this frequency range appear to be about

an order of magnitude larger than those calculated.

Weir (2001), following on the work of Gregor and Rumpf (1975), uses

a similar perturbation analysis with somewhat diﬀerent basic equations to

generate dispersion relations as a function of frequency and volume fraction.

Acknowledging that solutions of this dispersion relation yield a number of

propagation velocities including both kinematic and dynamic wave speeds

(see section 15.7.3), Weir chooses to focus on the dynamic or acoustic waves.

He demonstrates that, in general, there are two types of dynamic wave. These

have the same kinds of high and low frequency asymptotes described above.

The two low frequency wave speeds converge to yield a single dynamic wave

speed that has a functional dependence on frequency and α that is qualita-

tively similar to that of Atkinson and Kyt¨omaa (1992). It also agrees well

with the measured sound speeds in Musmarra et al.(1995) for suspensions

of various types of particles in liquid. Weir also analyzes the wave speeds in

ﬂuidized beds and compares them with those in unﬂuidized or static beds.

He also examines the data on wave attenuation; as with the other attenu-

ation data the experimental measurements are quite scattered and do not

agree well with the theoretical predictions, particularly at high frequencies.

9.3.3 Sonic speed with change of phase

Turning now to the behavior of a two-phase rather than two-component

mixture, it is necessary not only to consider the additional thermodynamic

constraint required to establish the mass exchange, δm, but also to recon-

sider the two thermodynamic constraints, QA and QB, that were implicit in

the two-component analysis of section 9.3.1, in the choice of the polytropic

index, k, for the gas and the choice of the sonic speed, c

, for the liquid. Note

that a nonisentropic choice for k (for example, k =1)impliesthatheatis

exchanged between the components, and yet this heat transfer process was

not explicitly considered, nor was an overall thermodynamic constraint such

as might be placed on the global change in entropy.

We shall see that the two-phase case requires more intimate knowledge of

these factors because the results are more sensitive to the thermodynamic

constraints. In an ideal, inﬁnitely homogenized mixture of vapor and liq-

uid the phases would everywhere be in such close proximity to each other

227

that heat transfer between the phases would occur instantaneously. The en-

tire mixture of vapor and liquid would then always be in thermodynamic

equilibrium. Indeed, one model of the response of the mixture, called the

homogeneous equilibrium model, assumes this to be the case. In practice,

however, there is a need for results for bubbly ﬂows and mist ﬂows in which

heat transfer between the phases does not occur so readily. A second com-

mon model assumes zero heat transfer between the phases and is known as

the homogeneous frozen model. In many circumstances the actual response

lies somewhere between these extremes. A limited amount of heat transfer

occurs between those portions of each phase that are close to the interface.

In order to incorporate this in the analysis, we adopt an approach that in-

cludes the homogeneous equilibrium and homogeneous frozen responses as

special cases but that requires a minor adjustment to the analysis of section

9.3.1 in order to reﬂect the degree of thermal exchange between the phases.

As in section 9.3.1 the total mass of the phases A and B after application of

the incremental pressure, δp,areρ

+ δm and ρ

− δm, respectively.

We now deﬁne the fractions of each phase, 

and 

that, because of their

proximity to the interface, exchange heat and therefore approach thermody-

namic equilibrium with each other. The other fractions (1 − 

)and(1− 

)

are assumed to be eﬀectively insulated so that they behave isentropically.

This is, of course, a crude simpliﬁcation of the actual circumstances, but it

permits qualitative assessment of practical ﬂows.

It follows that the volumes of the four fractions following the incremental

change in pressure, δp,are

(1 − 

)(ρ

+ δm)

[ρ

+ δp(∂ρ

/∂p)

]

;



(ρ

+ δm)

[ρ

+ δp(∂ρ

/∂p)

]

(1 − 

)(ρ

− δm)

[ρ

+ δp(∂ρ

/∂p)

]

;



(ρ

− δm)

[ρ

+ δp(∂ρ

/∂p)

]

(9.15)

where the subscripts s and e refer to isentropic and phase equilibrium deriva-

tives, respectively. Then the change in total volume leads to the following

modiﬁed form for equation 9.10 in the absence of surface tension:

ρc

=(1− 

)



∂ρ

∂p



+ 



∂ρ

∂p



+(1− 

)



∂ρ

∂p



+



∂ρ

∂p



−

δm

δp



−



(9.16)

The exchange of mass, δm, is now determined by imposing the constraint

that the entropy of the whole be unchanged by the perturbation. The entropy

228