Brennen Ch.E. Fundamentals of Multiphase Flow

Подождите немного. Документ загружается.

Figure 7.16. Left: X-ray image of ﬂuidized bed bubble (about 5cm in

diameter) in a bed of glass beads (courtesy of P.T.Rowe). Right: View from

above of bubbles breaking the surface of a sand/air ﬂuidized bed (courtesy

of J.F.Davidson).

have many similarities to the spherical cap bubbles discussed in section

3.2.2. The rise velocity, W

may be either faster or slower than the upward

velocity of the suspending ﬂuid, u

, and this implies two types of bubbles

that Catipovic et al. (1978) call fast and slow bubbles respectively. Figure

7.17 qualitatively depicts the nature of the streamlines of the ﬂow relative to

the bubbles for fast and slow bubbles. The same paper provides a ﬂow regime

map, ﬁgure 7.18 indicating the domains of fast bubbles, slow bubbles and

rapidly growing bubbles. When the particles are smaller other forces become

important, particularly those that cause particles to stick together. In gas

ﬂuidized beds the ﬂow regime map of Geldart (1973), reproduced as ﬁgure

7.19, is widely used to determine the ﬂow regime. With very small particles

(Group C) the cohesive eﬀects dominate and the bed behaves like a plug,

though the suspending ﬂuid may create holes in the plug. With somewhat

larger particles (Group A), the bed exhibits considerable expansion before

bubbling begins. Group B particles exhibit bubbles as soon as ﬂuidization

begins (fast bubbles) and, with even larger particles (Group D), the bubbles

become slow bubbles.

Aspects of the ﬂow regime maps in ﬁgures 7.18 and 7.19 qualitatively re-

ﬂect the results of the instability analysis of the last section. Larger particles

189

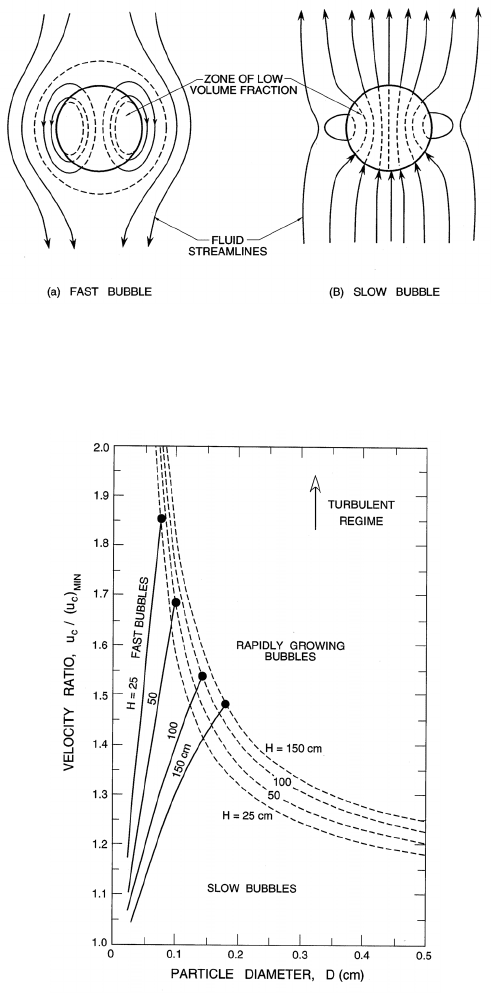
Figure 7.17. Sketches of the ﬂuid streamlines relative to a ﬂuidized bed

bubble of low volume fraction for a fast bubble (left) and a slow bubble.

Adapted from Catipovic et al. (1978).

Figure 7.18. Flow regime map for ﬂuidized beds with large particles (di-

ameter, D)where(u

)

min

is the minimum ﬂuidization velocity and H is

the height of the bed. Adapted from Catipovic et al. (1978).

190

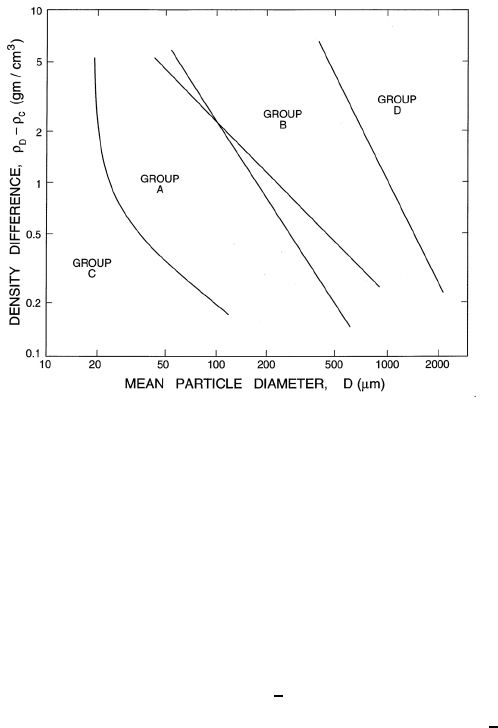
Figure 7.19. Flow regime map for ﬂuidized beds with small particles (di-

ameter, D). Adapted from Geldart (1973).

and larger ﬂuid velocities imply larger j

values and therefore, according

to instability analysis, larger growth rates. Thus, in the upper right side of

both ﬁgures we ﬁnd rapidly growing bubbles. Moreover, in the instability

analysis it transpires that the ratio of the wave speed, ω/κ (analogous to the

bubble velocity) to the typical ﬂuid velocity, j

, is a continuously decreas-

ing function of the parameter, j

/(g/κ)

. Indeed, ω/j

κ decreases from

values greater than unity to values less than unity as j

/(g/κ)

increases.

This is entirely consistent with the progression from fast bubbles for small

particles (small j

) to slow bubbles for larger particles.

For further details on bubbles in ﬂuidized beds the reader is referred to

the extensive literature including the books of Zenz and Othmer (1960),

Cheremisinoﬀ and Cheremisinoﬀ (1984), Davidson et al. (1985) and Gibilaro

(2001).

7.5 LIMITS ON SEPA RATED FLOW

We now leave disperse ﬂow limits and turn to the mechanisms that limit

separated ﬂow regimes.

191

7.5.1 Kelvin-Helmoltz instability

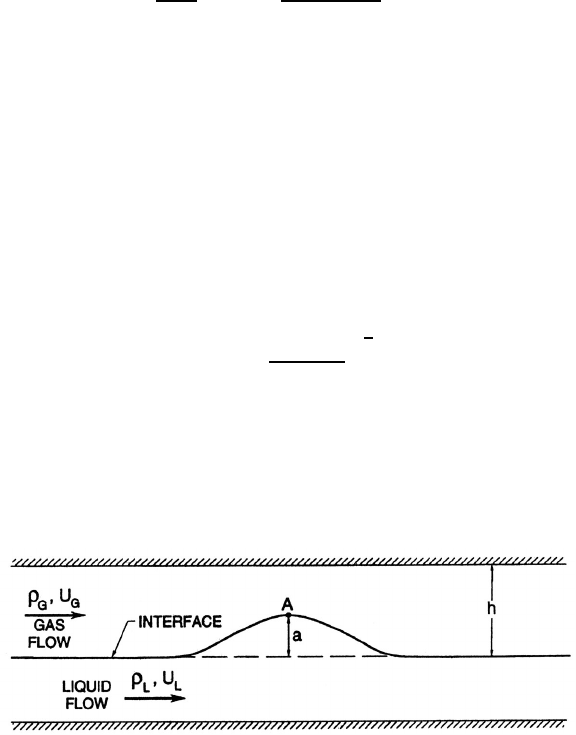
Separated ﬂow regimes such as stratiﬁed horizontal ﬂow or vertical annular

ﬂow can become unstable when waves form on the interface between the two

ﬂuid streams (subscripts 1 and 2). As indicated in ﬁgure 7.20, the densities

of the ﬂuids will be denoted by ρ

and ρ

and the velocities by u

and u

If these waves continue to grow in amplitude they will cause a transition to

another ﬂow regime, typically one with greater intermittency and involving

plugs or slugs. Therefore, in order to determine this particular boundary of

the separated ﬂow regime, it is necessary to investigate the potential growth

of the interfacial waves, whose wavelength will be denoted by λ (wavenum-

ber, κ =2π/λ). Studies of such waves have a long history originating with

the work of Kelvin and Helmholtz and the phenomena they revealed have

come to be called Kelvin-Helmholtz instabilities (see, for example, Yih 1965).

In general this class of instabilities involves the interplay between at least

two of the following three types of forces:

a buoyancy force due to gravity and proportional to the diﬀerence in the densities

of the two ﬂuids. This can be characterized by g

∆ρ where ∆ρ = ρ

− ρ

, g is

the acceleration due to gravity and  is a typical dimension of the waves. This

force may be stabilizing or destabilizing depending on the orientation of gravity,

g, relative to the two ﬂuid streams. In a horizontal ﬂow in which the upper ﬂuid

is lighter than the lower ﬂuid the force is stabilizing. When the reverse is true

the buoyancy force is destabilizing and this causes Rayleigh-Taylor instabilities.

When the streams are vertical as in vertical annular ﬂow the role played by the

buoyancy force is less clear.

a surface tension force characterized by S that is always stabilizing.

a Bernoulli eﬀect that implies a change in the pressure acting on the interface

caused by a change in velocity resulting from the displacement, a of that surface.

For example, if the upward displacement of the point A in ﬁgure 7.21 were to cause

an increase in the local velocity of ﬂuid 1 and a decrease in the local velocity of

ﬂuid 2, this would imply an induced pressure diﬀerence at the point A that would

Figure 7.20. Sketch showing the notation for Kelvin-Helmholtz instability.

192

increase the amplitude of the distortion, a. Such Bernoulli forces depend on the

diﬀerence in the velocity of the two streams, ∆u = u

− u

, and are characterized

by ρ(∆u)



where ρ and  are a characteristic density and dimension of the ﬂow.

The interplay between these forces is most readily illustrated by a simple

example. Neglecting viscous eﬀects, one can readily construct the planar, in-

compressible potential ﬂow solution for two semi-inﬁnite horizontal streams

separated by a plane horizontal interface (as in ﬁgure 7.20) on which small

amplitude waves have formed. Then it is readily shown (Lamb 1879, Yih

1965) that Kelvin-Helmholtz instability will occur when

g∆ρ

+ Sκ −

(∆u)

+ ρ

< 0 (7.21)

The contributions from the three previously mentioned forces are self-

evident. Note that the surface tension eﬀect is stabilizing since that term

is always positive, the buoyancy eﬀect may be stabilizing or destabilizing

depending on the sign of ∆ρ and the Bernoulli eﬀect is always destabiliz-

ing. Clearly, one subset of this class of Kelvin-Helmholtz instabilities are

the Rayleigh-Taylor instabilities that occur in the absence of ﬂow (∆u =0)

when ∆ρ is negative. In that static case, the above relation shows that the

interface is unstable to all wave numbers less than the critical value, κ = κ

where



g(−∆ρ)



(7.22)

In the next two sections we shall focus on the instabilities induced by the

destabilizing Bernoulli eﬀect for these can often cause instability of a sepa-

rated ﬂow regime.

Figure 7.21. Sketch showing the notation for stratiﬁed ﬂow instability.

193

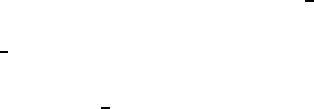
7.5.2 Stratiﬁed ﬂow instability

As a ﬁrst example, consider the stability of the horizontal stratiﬁed ﬂow

depicted in ﬁgure 7.21 where the destabilizing Bernoulli eﬀect is primarily

opposed by a stabilizing buoyancy force. An approximate instability condi-

tion is readily derived by observing that the formation of a wave (such as

that depicted in ﬁgure 7.21) will lead to a reduced pressure, p

, in the gas in

the oriﬁce formed by that wave. The reduction below the mean gas pressure,

¯p

, will be given by Bernoulli’s equation as

− ¯p

= −ρ

a/h (7.23)

provided a  h. The restraining pressure is given by the buoyancy eﬀect

of the elevated interface, namely (ρ

− ρ

)ga. It follows that the ﬂow will

become unstable when

>gh∆ρ/ρ

(7.24)

In this case the liquid velocity has been neglected since it is normally small

compared with the gas velocity. Consequently, the instability criterion pro-

vides an upper limit on the gas velocity that is, in eﬀect, the velocity diﬀer-

ence. Taitel and Dukler (1976) compared this prediction for the boundary

of the stratiﬁed ﬂow regime in a horizontal pipe of diameter, d,withthe

experimental observations of Mandhane et al. (1974) and found substantial

agreement. This can be demonstrated by observing that, from equation 7.24,

= αu

= C(α)α(gd∆ρ/ρ

)

(7.25)

where C(α)=(h/d)

is some simple monotonically increasing function of α

that depends on the pipe cross-section. For example, for the 2.5cm pipe of

ﬁgure 7.3 the factor (gd∆ρ/ρ

)

in equation 7.25 will have a value of approx-

imately 15m/s. As can be observed in ﬁgure 7.3, this is in close agreement

with the value of j

at which the ﬂow at low j

departs from the stratiﬁed

regime and begins to become wavy and then annular. Moreover the fac-

tor C(α)α should decrease as j

increases and, in ﬁgure 7.3, the boundary

between stratiﬁed ﬂow and wavy ﬂow also exhibits this decrease.

7.5.3 Annular ﬂow instability

As a second example consider vertical annular ﬂow that becomes unstable

when the Bernoulli force overcomes the stabilizing surface tension force.

From equation 7.21, this implies that disturbances with wavelengths greater

194

than a critical value, λ

, will be unstable and that

=2πS(ρ

+ ρ

)/ρ

(∆u)

(7.26)

For a liquid stream and a gas stream (as is normally the case in annular

ﬂow) and with ρ

 ρ

this becomes

=2πS/ρ

(∆u)

(7.27)

Now consider the application of this criterion to the ﬂow regime maps for

vertical pipe ﬂow included in ﬁgures 7.6 and 7.8. We examine the stability of

a well-developed annular ﬂow at high gas volume fraction where ∆u ≈ j

Then for a water/air mixture equation 7.27 predicts critical wavelengths

of 0.4cm and 40cm for j

=10m/s and j

=1m/s respectively. In other

words, at low values of j

only larger wavelengths are unstable and this

seems to be in accord with the break-up of the ﬂow into large slugs. On

the other hand at higher j

ﬂow rates, even quite small wavelengths are

unstable and the liquid gets torn apart into the small droplets carried in the

core gas ﬂow.

195

INTERNAL FLOW ENERGY CONVERSION

8.1 INTRODUCTION

One of the most common requirements of a multiphase ﬂow analysis is the

prediction of the energy gains and losses as the ﬂow proceeds through the

pipes, valves, pumps, and other components that make up an internal ﬂow

system. In this chapter we will attempt to provide a few insights into the

physical processes that inﬂuence these energy conversion processes in a mul-

tiphase ﬂow. The literature contains a plethora of engineering correlations

for pipe friction and some data for other components such as pumps. This

chapter will provide an overview and some references to illustrative material,

but does not pretend to survey these empirical methodologies.

As might be expected, frictional losses in straight uniform pipe ﬂows have

been the most widely studied of these energy conversion processes and so we

begin with a discussion of that subject, focusing ﬁrst on disperse or nearly

disperse ﬂows and then on separated ﬂows. In the last part of the chapter,

we consider multiphase ﬂows in pumps, in part because of the ubiquity of

these devices and in part because they provide a second example of the

multiphase ﬂow eﬀects in internal ﬂows.

8.2 FRICTIONAL LOSS IN DISPERSE FLOW

8.2.1 Horizontal Flow

We begin with a discussion of disperse horizontal ﬂow. There exists a sub-

stantial body of data relating to the frictional losses or pressure gradient,

(−dp/ds), in a straight pipe of circular cross-section (the coordinate s is

measured along the axis of the pipe). Clearly (−dp/ds) is a critical factor

in the design of many systems, for example slurry pipelines. Therefore a

substantial data base exists for the ﬂows of mixtures of solids and water

196

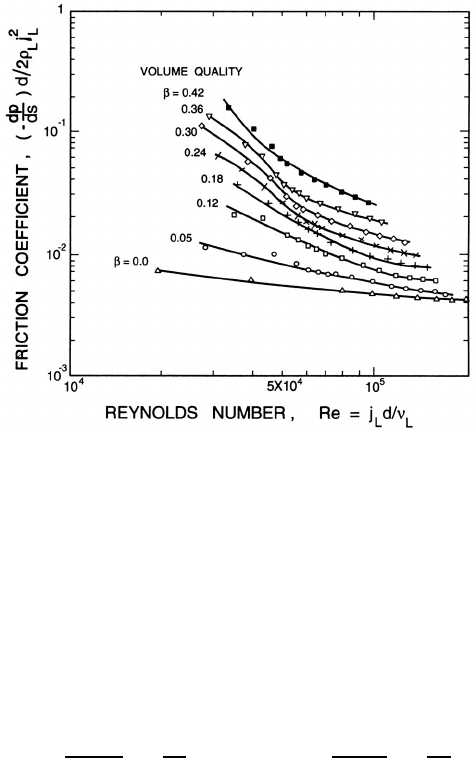
Figure 8.1. Typical friction coeﬃcients (based on the liquid volumetric

ﬂux and the liquid density) plotted against Reynolds number (based on the

liquid volumetric ﬂux and the liquid viscosity) for the horizontal pipeline

ﬂow (d =5.2cm)ofsand(D =0.018cm)andwaterat21

◦

C (Lazarus and

Neilson 1978).

in horizontal pipes. The hydraulic gradient is usually non-dimensionalized

using the pipe diameter, d, the density of the suspending phase (ρ

if liq-

uid), and either the total volumetric ﬂux, j, or the volumetric ﬂux of the

suspending ﬂuid (j

if liquid). Thus, commonly used friction coeﬃcients are

2ρ



−



or C

2ρ



−



(8.1)

and, in parallel with the traditional Moody diagram for single phase ﬂow,

these friction coeﬃcients are usually presented as functions of a Reynolds

number for various mixture ratios as characterized by the volume fraction, α,

or the volume quality, β, of the suspended phase. Commonly used Reynolds

numbers are based on the pipe diameter, the viscosity of the suspending

phase (ν

if liquid) and either the total volumetric ﬂux, j, or the volumetric

ﬂux of the suspending ﬂuid.

For a more complete review of slurry pipeline data the reader is referred to

Shook and Roco (1991) and Lazarus and Neilsen (1978). For the solids/gas

ﬂows associated with the pneumatic conveying of solids, Soo (1983) provides

a good summary. For boiling ﬂows or for gas/liquid ﬂows, the reader is

197

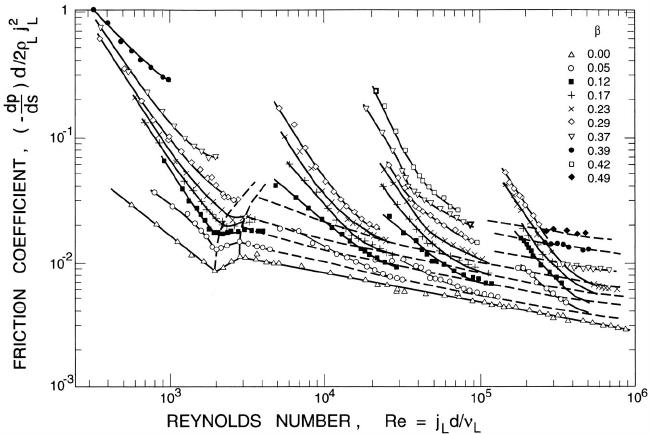
Figure 8.2. Typical friction coeﬃcients (based on the liquid volumetric

ﬂux and the liquid density) plotted against Reynolds number (based on the

liquid volumetric ﬂux and the liquid viscosity) for the horizontal pipeline

ﬂow of four diﬀerent solid/liquid mixtures (Lazarus and Neilson 1978).

referred to the reviews of Hsu and Graham (1976) and Collier and Thome

(1994).

The typical form of the friction coeﬃcient data is illustrated in ﬁgures 8.1

and 8.2 taken from Lazarus and Neilson (1978). Typically the friction co-

eﬃcient increases markedly with increasing concentration and this increase

is more signiﬁcant the lower the Reynolds number. Note that the measured

increases in the friction coeﬃcient can exceed an order of magnitude. For

a given particle size and density, the ﬂow in a given pipe becomes increas-

ingly homogeneous as the ﬂow rate is increased since, as discussed in section

7.3.1, the typical mixing velocity is increasing while the typical segregation

velocity remains relatively constant. The friction coeﬃcient is usually in-

creased by segregation eﬀects, so, for a given pipe and particles, part of the

decrease in the friction coeﬃcient with increasing ﬂow rate is due to the

normal decrease with Reynolds number and part is due to the increasing

homogeneity of the ﬂow. Figure 8.2, taken from Lazarus and Neilson, shows

how the friction coeﬃcient curves for a variety of solid-liquid ﬂows, tend

to asymptote at higher Reynolds numbers to a family of curves (shown by

the dashed lines) on which the friction coeﬃcient is a function only of the

Reynolds number and volume fraction. These so-called base curves pertain

198