Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

(5.75)

Средняя квадратическая ошибка «измерения» величин или х

равна

8 403

—- = 1,45, а величин I/ равна т> = —: — 1,02 (с. к. о.

4 У2

01 = 1).

§ 49. УРАВНИВАНИЕ ПРИ БОЛЬШОМ ЧИСЛЕ НЕИЗВЕСТНЫХ

При уравнивании обширных геодезических сетей приходится со-

ставлять системы нормальных уравнений с большим числом неиз-

вестных (например, порядка 500 ООО). Решение таких систем представ-

ляет собой сложную научную и техническую проблему даже с приме-

нением быстродействующих ЭВМ. Уменьшения числа совместно ре-

шаемых уравнений можно достичь, применяя так называемый

многогрупповой способ в параметрической форме, предложенный

И. Ю. Пранис-Праневичем. Для этого уравниваемую сеть делят на

участки, по граничной линии которых находятся так называемые

связующие пункты. Неизвестные, соответствующие этим пунктам,

нумеруются последними вслед за неизвестными, относящимися к внут-'

ренним пунктам. Если обозначить векторы этих неизвестных через А

и Д

, то общую систему нормальных уравнений, например, для числа

участков 5=3 можно записать в виде

ЯА + ЯьсА + Ь

= 0 ;)

+ Я

.<А + Ь

= 0;

з + Я

.<А + Ь

= 0;

Я1.<А + #2.ОД

+ /?з.оА,+Л

До+ Ь

= 0.

Первые три уравнения называют частично независимыми, а послед-

нее — связующим. Выражая в каждом участке неизвестные АI по

формуле

Д^-ЯГ'ЯьА - КГ

= -яг' (Я

А + Ь), (5.76)

после подстановки (5.76) в связующее уравнение найдем преобразо-

ванное уравнение

[Я

• 5] Д

+ [Ь

• з] = 0. (5.77)

Матрица [/?„. в] = — 2 ^.о^г ^-о'

а вектор [Ь

.5] = Ь

— 2 Я® Ь

{

1=1

Матрица /?

может быть получена из матриц составляемых

в каждом участке, как их сумма, т. е. /?

= ^ ^ о'- Тогда

[Яо.5] = 2 1].

314.

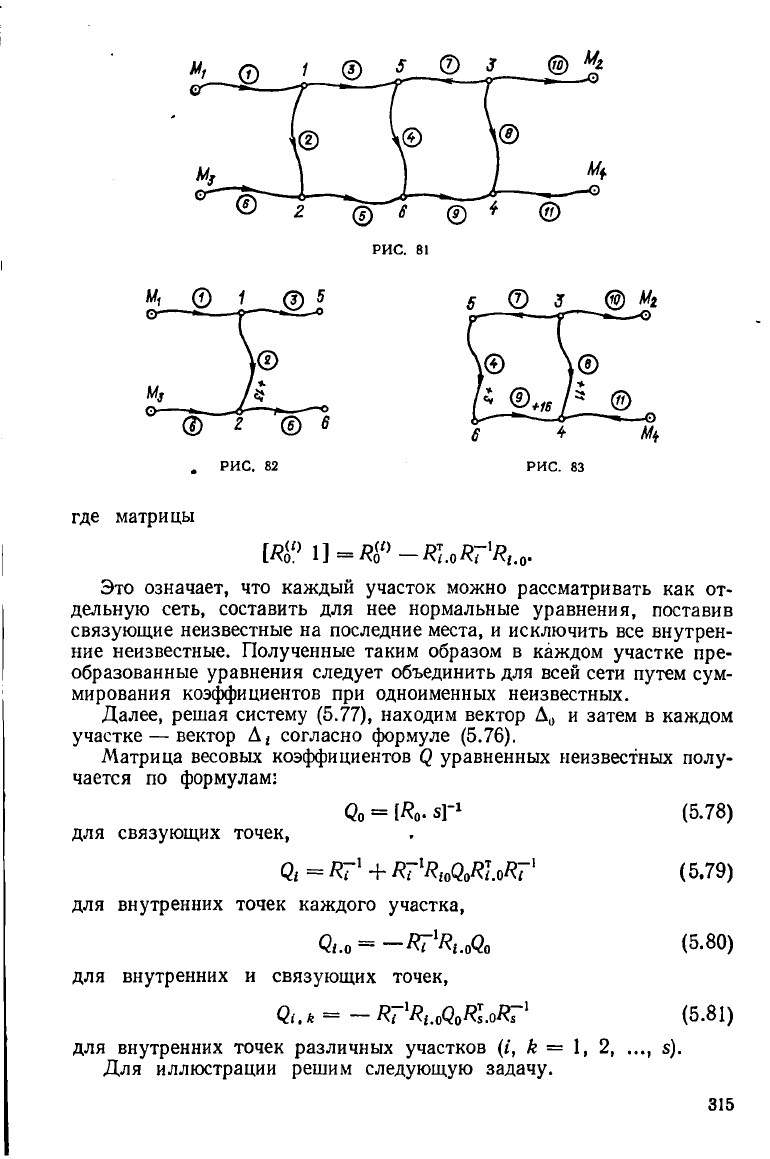
РИС. 81

где матрицы

1] = № —'Л/. о-

Это означает, что каждый участок можно рассматривать как от-

дельную сеть, составить для нее нормальные уравнения, поставив

связующие неизвестные на последние места, и исключить все внутрен-

ние неизвестные. Полученные таким образом в каждом участке пре-

образованные уравнения следует объединить для всей сети путем сум-

мирования коэффициентов при одноименных неизвестных.

Далее, решая систему (5.77), находим вектор Д

и затем в каждом

участке — вектор Д

согласно формуле (5.76).

Матрица весовых коэффициентов ф уравненных неизвестных полу-

чается по формулам:

С= [Яо- з]"

(5.78)

для связующих точек,

СЬ = Я"

+ Я7

ЯМ1ОК7

]

(5.79)

для внутренних точек каждого участка,

С^.о^-ЯГ'адо (5.80)

для внутренних и связующих точек,

<2<.

* = - ДГ'Яг.оОо^.оЯГ

(5.81)

для внутренних точек различных участков («, к = 1,2, 5).

Для иллюстрации решим следующую задачу.

315.

Таблица

118

Исходные

марки

Отметка, м

Номера хо-

дов

Номера хо-

дов

Л*1

101>528

1,234

3,883

105,830 2 2,482

6,049

108,553 3

4,822

9 1,995

104,342 4

0,180

10 2,118

2,504

1,219

0,915

5.28. Выполнить уравнивание нивелирной сети (рис. 81), разделив ее на два

участка, показанных на рис. 82 и рис. 83. Исходные данные приведены в табл.

155. Длины ходов для простоты приняты одинаковыми.

Решение. Прежде всего в каждом участке вычислим приближенные

отметки узловых точек:

в 1-м участке во 2-м участке

х<°> = Я, +Н

= 102,762, ' *<°> = //,-*,„= 103,712,

лг<°> = Н

+ Л, = 105,257, *<°> = Я

+ Л

= 109,772.

х<°> = х{

+ Л

= 107,584,

= 4

+ Ъ = Ю7,761,

По способу узлов проф. В. В. Попова (см. § 34) составляем системы нормаль-

ных уравнений в каждом участке. Свободные члены уравнений поправок, вы-

численные по формуле = 4°

— + Л(), выписаны на рис. 82 и 83

(в мм).

1 участок. Нормальные уравнения:

38*1 —8*2—8*5 — 13 = 0;

— 8*,+35*

— 8*, +13=0;

— о*, + 8*

= 0;

-8*, +8*

= 0.

Поэтому матрицы равны

*'•=-('.)=-§ «Р-С.К-

/0,375 +0,125\ , _

"40.125 0.375У' '

Преобразованный вектор свободных членов

г л „т „ 1 ^ /0\ / 0,375 0,125\ /— 13\ /—3,25\

[ .!] = *„- /?1.

/?Г'

ьо = ( о ) + (

о, 125 0,375) 4 13 /

(+ 3,25/ *

316

Следовательно, получаем преобразованную систему нормальных уравнений

0,6258л:

— 0,1258*„ —3,25 = 0; 1

— 0,1258*

+ 0,6258*, +3,25 = 0. )

2 участок. Нормальные уравнения:

38*з — 8*

— 8*5 = 0;

— 8*

+ 38*

— 8*, + 27 = 0

— 5*3 28*6 — 8*„ — 8 = 0

— 8*

— 8*6 + 28*, — 19 = 0

Как и в первом участке, матрица = К2.0 = /?|.о. а матрицы

Преобразованный вектор свободных членов

о 19 / ^0.125 0,375/ \27/ 8,875 ]

и преобразованная система нормальных уравнений

1,6258*6 — 1,1255*, —4,625 = 0; 1

— 1,1258*6 + 1,6258*,—8,875 = 0. /

(6,83

Суммируя уравнения (5.82) и (5.83), находим преобразованную связующую

систему нормальных уравнений (5.77)

2,2505*6 — 1,2508*„ — 7,875 = 0;

— 1,250а*б +2,2508*, —5,625 = 0.

Решая ее путем обращения матрицы коэффициентов, получаем матрицу

„ , /0,643 0,357\

<г

°=

[/?

°-

= (о,357 0,643/

(5 84

и неизвестные

Далее по формуле (5.76) вычисляем поправки неизвестных в каждом участке

/8*1 \ /0,375 0,1254 ((- 7,072 \ /- 13 \1 /6,706\

\Ъ

Х1

) ^0,125 0,375/ —6,428/ \ 13/| 1,0,044/»

/8*

/0,375 0,125\ <У-7,072\ ,/0\1 / 0,080\

\8*

/ \0,125 0,375/ 1\—6,428/ \27/| ^—6,830/'

Ниже по формуле = 6*

нач

— 6*кон + вычислены поправки превышений-

Номера ходов 1 2 3 4 56 7 8 9 10 11

6,7 6,3 0,4 —3,6 6,4 0 —4,0 4,1 2,8 —0,1 -в.»

Контролем вычислений является равенство 2 ± р^ = 0, которое должно вы»

1*1

полниться для каждого угла /.

317.

Для вычисления матрицы <2 согласно формулам (5.80), (5.81) находим мат-

рицы*

-1 -I /0,286 0,214\

Л* *1.ово = Я

«а.оО.- ^

0 214

о,28б]~ '-

т /0,134 0,116\

Кг^ЛЪ-оКг — 1,0,116 0,134/ ~~

и далее по формуле (5.79)

_ /0,509 0,241\

—

<Эг

— (^0 241 0,509/'

Наконец, полная матрица

0,241 0,134

116 0,286

0,214

0,509

0,116

,134 0,214

0,286

0,509

241

0,286

0,214

509

0,214

0,286

0,643

0,357

0,643

Преобразованные уравнения в каждом участке можно получить и в схеме

Гаусса. Так, например, эти вычисления для второго участка выполнены в табл.

156.

Ее особенностью является то, что исключение неизвестных 6*5 и 6дт

не про-

изводится, а вычисляются лишь преобразованные алгоритмы Гаусса [сс.2],

[сЛ.2], [с/.2], [М.2],

[Л

1.2]. Неизвестные б*в и 6х

выписываются в нее после ре-

* Заметим, что при перемножении нескольких матриц целесообразно сна-

чала получать промежуточные матрицы с меньшими размерами [13].

Таблица 156

Вспомогат.

величины

Ьх„

8*.

5*.

1 5

Контроль

(0,3333)

3,00

(-1)

—1,00

+0,333

—1,00

+0,333

1,00

-0,333 -

1,00

-0,334

(0,3745)

2,67

(-1)

—0,33

0,125

—1,00

0,375

+27

—10,125

28,33

— 10,625

28,33

— 10,625

1,62

—1,12

1,62

—4,62

-8,88

—4,13

—8,28

Ьх]

0,08

—6,83

7,07 6,43

0,508

0,240

0,508

0,286 0,214

Чг.а

0,214 0,286

0,286 0,214

<Э

0,214

-° 0,286

0,643 0,357

<2о

0,357 0,643

318.

шения суммарной системы, а затем, как обычно, вычисляются неизвестные и.

6*4- Аналогичным образом вычисляется матрица весовых коэффициентов (ее

Левый нижний блок получен путем обращения матрицы [/?

-2]; дальнейшие

вычисления выполняются по способу Ганзена, как обычно).

Оценка точности.

1) Величина [от] = 226,56.

Контроль вычисления [рVV] можно выполнить по формуле

\рт\ = [рЩ + РА = [

Щ + 2 ДгЪ +

До

с о .

1=1

где Ь и Д — соответственно векторы свободных членов и неизвестных нормаль-

ных уравнений.

В нашей задаче

[т] = 676+ (6,7 0) + (0,1 -6,8) ^ ^ V (7,1 6,4) ^^ = 227. .

Средняя квадратическая ошибка на 1 км хода т = ~у = 6,7 мм.

2) Средние квадратические ошибки уравненных отметок узловых точек

Х/

= тУЩ.

Например, т

Хь

= т

х>

= 6,7 У0,64 = 5,4 мм.

3) Средние квадратические ошибки уравненных превышений вычисляем по

формуле т

= " / Р*

где

Рн

« V Ч

к}

Ом /\ 1

если 1 и к — соответственно номера начальных и конечных точек 1-го хода.

5.29. Получить по схеме Гаусса преобразованную систему нормальных урав-

нений, неизвестные и матрицу для 1-го участка.

5.30. Решить предыдущую задачу без разделения сети на участки и срав-

нить результаты.

5.31. Выполнить уравнивание нивелирной сети из задачи 3.52, разделив

ее на два участка, отнеся в первый участок ходы 1—4, во второй —'5, 6, 7, 8

(см. рис. 81).

§ 50. УРАВНИВАНИЕ С УЧЕТОМ ОШИБОК ИСХОДНЫХ ДАННЫХ

До сих пор мы рассматривали случаи, когда исходные данные

(координаты пунктов, дирекционные углы и длины сторон) прини-

мались безошибочными. Однако эти величины сами определяются из

измерений и содержат ошибки, пренебречь которыми часто не пред-

ставляется возможным. Поэтому возникает задача уравнивания с уче-

том ошибок исходных данных и исследования их влияния на элементы

уравниваемой сети. Рассмотрим кратко решение этих задач при пара-

метрическом и коррелатном способах.

Параметрический способ. Обозначим.вектор попра-

вок вновь определяемых неизвестных, как и ранее, через Ах, а попра-

вок к исходным данным, которые также будем определять из уравни-

319.

вания, через Аг. Тогда можно написать два матричных уравнения

поправок [7]

V, = А Ах + А

Аг + Ь, (5.85)

Аг.

(5.86)

Так как результаты измерений и исходные данные независимы, то

имеем условие

V] РУ,+ VI Ру

= ппп, (5.87)

где Р

— матрица весов исходных данных, полагаемая известной.

Условие (5.87) приводит к системе нормальных уравнений

где матрица

лН

АГРА, А]РА

А] РА, А

.РА

+ Р

(5.88)

(5.89)

а векторы

Ь, = А

РЦ Ь

=А

РЬ.

1 2

Как видно из формулы (5.89), матрица Я отличается от матрицы

нормальных уравнений, составляемой при обычном параметрическом

способе, У? = А*РА при А — лишь тем, что к ее нижнему бло-

ку коэффициентов при поправках Аг прибавляется матрица весов этих

поправок. Поэтому, не делая различия между неизвестными Дл; и Дг,

матрицу /? можно составить обычным образом, не обращая внимания

на формулу (5.86), присоединив к ней затем матрицу Р

. Последняя,

вообще говоря, не является диагональной, так как исходные данные

зависимы (коррелированы).- Однако для упрощения вычислений ее

часто принимают диагональной, что оправдано, если исходные данные

значительно удалены друг от друга и корреляция между ними слаба.

Обращение матрицы (5.89) приводит к матрице весовых коэффи-

циентов

определяемых неизвестных и исходных данных. Заметим, что если бы

исходные данные были безошибочны, то От —

В противном случае

а также <з\, = + Да1 ,

] 1

где через о- обозначено среднее квадратическое отклонение урав-

ленных неизвестных при безошибочных исходных данных.

320

В силу известного критерия ничтожных погрешностей исходные

данные можно считать безошибочными, если

До* < 0,114 ,

]

)

или №

)л < 0,11 (<2

)„.

Решим следующую задачу.

(5.90)

5.32. Пусть на станции между двумя заданными с точностью а_ = а„ =•

I II

= 1" дирекционными углами измерены три угла у

с точностью = 2".

Измеренные и заданные величины углов приведены ниже. Требуется выполнить

уравнивание этих углов.

Дирекционные углы

«,= 10°00'00,0"

«,= 101 01 15,2

Секунды уравненных

углов

00,4

14,8

Измеренные углы

=25°00'10,0"

у,=35 50 50,5

{/,=30 10 09,2

Секунды уравненных

углов

11,6

52,1

10,8

Решение. Вычисляем приближенные значения углов

а<°> = о! + >

= 35°00'10,0",

= «I

У1~\~ Уг

— '70°51'00,5"

и составляем уравнения поправок для измеряемых углов

Ъх

1 —

Ьг

1 +

= — ь

Х1

+ Ьх

+ /

;

= — Ъх

+Ьг

+ 1

Свободные члены /ц = 'г = 0, а 1

='а

— а'®'— уз = +5,5". С помощью

табл. 157 коэффициентов уравнений поправок составляем нормальные уравнения

с матрицей

2 —1

—1 0

—1

— 1

—1 0

— 1 0

^12

Я К

Таблица 157

Неизвестные

Номера

углов

в*.

5г, Ьг,

— 1

—1

+ 1

5,5

1.57

1.58

1,57

1,96

3,54

0,39

—0,39

11 4-258

321

полагая вр менно Р

= 0, и вектором свободных членов

й=г

_5,5 1

(

Ь<

Примем в качестве дисперсии единицы веса Од = о' = 2

. Тогда веса

1, а р, = —1 = 4/1 и матрица

' «г

Поэтому матрица

4 Е.

2X2

Я =

2 —1

—1

2 0 —1

—1

0 5 0

—1

Обратная матрица, полученная путем разделения на блоки,

где

/Г

с?

0,667 0,333 \

0,333 0,667 / '

и = /гп

«I. = ЯП

(-Я = -V .

333 —0,333

333 4,333

(5.91)

-1 V""

(

Г1-<М

0,232 0,018

0,018 0,232

имеет вид

Вектор поправок

Д*

Дг

0,804 0,446 0,161 0,089

0,446 0,804 0,089 0,161

0,161 0,089 0,232 0,018

0,089 0,161 0,018 0,232

= — 06= (1,96 3,54 0,39 —0,39)

(5.92)

Вычисление поправок углов выполнено в табл. 157 по формуле (5.85). Урав-

нивание выполнено правильно, так как а,, — = 2уСправедливы гакже'

контрольные формулы = 0 и А1 РУ

+ Р

= 0, вытекающие из

322.

леммы Гаусса. Первое равенство проверить легко, а для второго с помощью табл.

157 получаем

1,57/ V—0,39/ V 0,01/

Так как из-за малого числа избыточных измерений (г = 5 — 4 = 1) вычис-

лить ошибку и невозможно, то, приняв ст

= 2, находим о~ = а~ =21/0,232=

I II V

= 0,96" (как видно, теоретически точность углов <Х] и а

в результате уравни-

вания повысилась), ст~ = а~ = 2 |/"0,804 =» 1,79".

Так как (Д(?Д^ = 0,137 > 0,11 ((?*)// = 0,073, то на основании формулы

(5.90) приходим к выводу, что исходные дирекционные углы нельзя принять без-

ошибочными.

5.33. Решить ту же задачу, приняв а

У1

= 3". Сделать вывод о возможнос-

ти принять исходные углы безошибочными в этом случае.

5.34. Выполнить с учетом ошибок исходных дирекционных углов уравни-

вание углов в задаче 3.27, приняв а

а1

= а

а11

= 1 , а

у[

= 2".

5.35. Для определения отметки точки к ней проложены два равноточных

хода, причем первый от марки, имеющей отметку на порядок точнее, чем исход-

ная марка второго хода. «Испортит» ли привязка ко второй марке искомую от-

метку?

Коррелатный способ. В этом случае условные уравнения сос-

тавляются как обычно, однако с той разницей, что они, кроме поправок непос-

редственных измерений, будут включать и поправки исходных данных, также

рассматриваемых как результаты измерений. Число условных уравнений равно

числу уравнений, возникающих при безошибочных исходных данных. Обозна-

чая поправки исходных данных через Дг, запишем условные уравнения в мат-

ричной форме в виде

В^ + В

Дг + Г = 0. (5.93)

Решая их под условием (5.87), получим нормальное уравнение ЫК + В

= 0, где теперь матрица

N^В

^В] + В

В^ = N

+ N

, (5.94)

а С = Р"

, СЬ = Р7' .

Как видно, при коррелатном способе число совместно решаемых уравнений

то же, что и при уравнивании при безошибочных исходных данных. В этом его

преимущество перед параметрическим способом.

Оценка точности функций выполняется, как и в обычном коррелатном спо-

собе, причем коэффициенты (» = 1, 2, ..., п, п + 1, ..., п + «, где « — число

поправок исходных данных) вычисляются как производные не только по К^, но

и по

Матрица обратных весов уравненных исходных данных может быть получе-

на по формуле

<2~=<Э

-С1

В1Ы-1В„Д

. (5.95)

Так как N «= Сщ, есть матрица обратных весов невязок (см. § 40), с учетом фор-

мулы (5.94) на основании критерия ничтожных погрешностей можно считать,

что исходные данные тогда не искажают невязки, когда для любого /

(^<0,11 (Л^. (5.96)

5.36. Решить коррелатным способом задачу 5.32.

Решение. Условное уравнение будет

+ + Ч + — Ц, +

в>

= 0,

11* 323

где невязка

Матрицы <? = Е, Р~

= 0,255 = (}

, В

•= (1 1 1), В

= (1 —1). Поэтому

нормальное уравнение

(3 + 0,5) к — 5,5 = 0. . (5.97)

Так как 0,5 ^ 0,11 • 3, то на основании выражения (5.96) нельзя сделать

вывод о пренебрегаемости ошибками исходных данных. Решая уравнение (5.97),

находим к = 5,5/3,5 = 1,57 и поправки

о, = о

= с

= 1,57"; 821 = 0,256 = 0,39"; Ц, = — 0,39".

Оценим точность функции о^ = а] + у

Имеем матрицу /=(10010). Алгоритмы [я//] = 1,25, [яа/] = 1,25.

Поэтому

у- = 1,25- 1,25

/3,5 = 0,804,

Аналогично для функции сч имеем /=(0 0 0 1 0), [я//] = 0,25, [яа/] = 0,25 и

-1— = 0,25 — 0,25

/3,5 = 0,232.

По формуле (5.95) получаем

т 0,062 /

—

0.~ =0,25Е — 0.252Й2 Л'"' В

= 0,25Е— -у^- ( ^

/ 0,232 0,018 \

\ 0,018 0,232 )

Как видим, результаты уравнивания совпадают с теми, которые получены при

параметрическом способе, но объем вычислений здесь маньше.