Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

2 — 1 0

0 0

1 4

— 1 — 1

0 — 1 2

— 1 0

— 1 — 1

— 1

5.13. Уравнять в условиях задач 3.38 и 3.27 измеренные углы в сети триан-

гуляции, приняв в качестве неизвестных дирекционные углы сторон. Оценить

точность уравненных длины стороны Сй и всех дирекционных углов.

Решение. Возникающие в этом случае уравнения поправок приведены

на стр. 186, а на стр. 172 — матрица <

Я =

и вектор свободных членов

/ 5,4

-8,6

Х<Р1 = —10,3

18,0

\-4,5

Величина [И] = 165,74.

Уравнение, связывающее неизвестные поправки дирекционных углов, при-

мет вид базисного условного уравнения

81П

( а, — а

) 8Ш (а

— а^ зш (а

— а

)

' 31п (а

— а

) • 51п (а

— а

) ЗШ (а

— а

)

= 1.

(5.42)

в котором измеренные углы у

(

выражены как разности дирекционных углов.

После логарифмирования получим 1 — 1§6

+ 2 ± 1§зш(ау — а^.) = 0,

а для приведения левой части к линейному виду находим частные производные

(д 1§81П (а) — а

)

дач

\ М (0, Л

)о

т' I

Й1§

31П

(а

}

— а

)

да

\ М (0)

1~т

где у\

(0) __

значения углов, вычисленных по приближенным дирекцнонным уг-

лам. Уравнение (5.42) теперь примет вид

± 2 (с»8 г/Г - с!в у1

) Ьа, +

= о

с невязкой

(5.43)

V = (1в

- 1е Ь

+ 2 ± 1

8ш «/<

>) • (5.44)

Для уравниваемой сети получим

(с»е

У\

+ у

)

8*1

— (с1б

+ у

) + у

с1§

) Ьх

—

юр

- (с(в

У*

+ с4в

Уъ)

Ь*4 + У, + с1§ у,) 8*6+ = 0. (5.45)

Можно указать следующее правило образования коэффициентов при по-

правках Ьх]\ они равны сумме котангенсов углов, примыкающих к стороне / и

участвующих в передаче длины сторон по цепочке, причем если углы располо-

жены по одну сторону от нее, то сумма берется со знаком «+», если по разную,

то со знаком «—».

Для вычисления коэффициентов удобно пользоваться калькуляторами

(например, «Электроника БЗ-21»), используя метод накопления. Применитель-

но к задаче 3.38 вычисляем приближенные углы у^

г/[°» = 64

35'55,5",

у<

°>

=55°19'55,5", г/1

= 69°27'52,6",

294.

= 49 30 19,3, {4°> = 55 20 32,8, = 33 44 19,4,

= 43 01 57,2,

и далее составляем табличку

Ноыера дирекционных углов 1 2 3 4 5

Номера углов 1,3 1,6 4,6 4,9 7,»

Коэффициенты 1,329 —0,849 1,066 1,763 2,686

Невязку вычисляем по формуле (5.44), но не по измеренным углам, а по

углам утакже с помощью калькулятора или по программе (см. прил. ХП1.7)-

С нашими данными, учитывая, что

1б Ь

= 3.2584263, 1е Ь

= 3.3295004,

ш = —3,05 • 10-» и ш = ш = —3,05 • 10? • 4,749 • 10"5 = — 14,486.

Итак, условное уравнение имеет вид

1,3293*! — 0,8495*2 + 1,0665*

— 1,7638*

+ 2,5688*

— 14,486 = 0.

Нетрудно убедиться, что коэффициенты этого уравнения получаются из

(4.75) путем замены поправок углов через поправки дирекционных углов и из-

менения знаков. Таким образом, получаем систему, аналогичную системе (6.37):

28^ — 6*

— 5*1 48*2 — 5*3

— Ъх, 25*о

+ 1,3296 +5,4 = 0

— 5*4 —0,8496 — 8,6 = 0

— 5*

+ 1,0666 — 10,3=0

— 8*з+45*

— 5*

— 1,7636 + 18,0=0

— 8*

+23*

+2,5686 — 4,5=0

1,3295*! —0,8495*

- +1,0665*

— 1,7638*

+2,5688*

— 14,486 = 0.

(5.46)

Ее можно решить, применяя схему Гаусса. В этом случае к табл. 49 доба-

вится еще одно эквивалентное и элиминационное уравнение. Однако здесь мы

применим иной способ решения, воспользовавшись знанием обратной матрицы

ф = /?

-1

, полученной в задаче 3.27 и равной

'0,611 0,222 0,167 0,111 0,056\

0,444 0,333 0,222 0,112

0 = | 0,833 0,333 0,167

0,444 0,222

0,611/

Вектор —<)А

1., который обозначим через 5, уже получен при решении

задачи 3.27 и равен (см. табл. 47)

'— 1,416 \

2,567 \

6 = I 5,322 I .

— 2,241 I

1,128/

Поэтому А* = —(}В

К + 6. Далее согласно формуле (5.38), учи-

тывая, что матрица

В - (1,329 — 0,849 1,066 — 1,763 2,568), получим

295.

/0,748\

/ 0,167 \

(2В

= I 0,667

\ 0,101 I

41,335/

(вычисления выполнены по программе прил. XIII.

для «Электроники БЗ-21»),

Матрица Ы_= В(}В-

= 4,813.

Невязка № = — Г — В5 = +14,489 — 8,460 - 6,028.

Из решения уравнений (5.39) 4,8136 + 6,028 = 0 находим коррелату

к = —1,252 и далее вектор

Поправки в углы вычисляем аналогично тому, как это сделано в задаче

3.27. В результате получаем вектор поправок V = А Ах + Ь = (—2,1 — 2,8 —

— 0,5 2,0 + 1,7 + 3,4 — 28 — 2,1 + 0,4)

, совпадающий с вектором поправок,

вычисленным в задаче 3.38, что и должно быть. О правильности вычислений

говорят также выполнения равенств (5.35).

Оценка точности. 1. Величина

[то] = 1М + 1'ААх+\Г*К = 165,74 + (5,4 — 8,6 — 10,3 18,0 — 4,5) X

/—0,480\

I 2,776 \

X I 6,157 1 — 14,49 (—1,252) = 42,81.

1-2,144 I

\ 2,799/

2. Согласно формуле (5.40) найдем матрицу весовых коэффициентов уравнен-

ных дирекционных углов. Будем иметь

0,748\

0,167 \

0,667 1.0,208(0,748 0,167 0,667 0,101 1,330) =

0,101 I

.1,334/

0,116 0,026 0,104 0,016 0,208\

0,006 0,023 0,004 0,046 \

Средняя квадратическая ошибка т =

42,81

0,092 0,014 0,185 |= ДО.

0,002 0,028 |

0,370/

Искомая матрица

296.

В частности, для дирекционного угла а

= х

1/^ = 0,741.

3. Для оценки точности длины стороны СО составляем функцию

Ь{ З1П

81П

уЬу 51П (а

—

)

Я1П

(а

— а4)

СО

51П (/{

51(1 </<

~ 51П К — =1) З!П (А

— А

)

или

«= 61 +

5111

( — а, ) +

1§

зт (п

— 04) — !б зш (а

— а

) — зт (а

— а

Приводя ее к линейному виду, найдем

= +

где

= у^

+ с1§ у\

= 1,329;

=с1§^

-с1

<) = 0,216;

= у<

= 0,692;

/4 = - (с*8У1°> +с4

</<°>) = - 1,387;

/б = 0,

поэтому [ = (1,329 0,216 0,692 — 1,387 0).

Изучающим предлагается самостоятельно сформулировать правило вы-

числения коэффициентов /у. Далее согласно формуле (5,41) по программе (см.

прил. XIII. 11) находим

-]Г~ = №хР = (0,613 0,267 0,221 —0,219 — 0,469)/

= 1,330.

Так как оцениваемая функция

то т

= т

/з- р.

Средняя квадратическая ошибка

= т =2,9^ 1,330 =3,34.

р 3,34 1

Поэтому = Ю

-5

= „._„„

' з р 2,062 61800

(в задаче 4.23 эта же величина получена равной 1/61 000).

5.14. Решить систему уравнений (5.46) в схеме Гаусса, выполнив также

оценку точности тех же функций, что и в предыдущей задаче.

5.15. Решить систему (5.46) по методу квадратных корней.

5.16. Составить в общем виде уравнения поправок для измеренных длив

сторон, дирекционных углов и направлений, если в качестве неизвестных при-

нять приращения координат.

Сколько условных уравнений возникает при уравнивании вставки в угол

(см. рис. 71) при таком выборе параметров?

Ответ. 6 условных уравнений вида

[®д*] + »х = о. [®дЛ+ю, = о

в каждом из трех треугольников.

297.

5.17. Выполнить уравнивание углов параметрическим способом с условия-

ми, приняв в качестве неизвестных приращения координат в условиях задачи'

4.23 и не принимая во внимание треугольник с углами 7, 8, 9.

5.18. Выполнить уравнивание углов этим же способом в условиях задачи

4.25, приняв в качестве параметров дирекционные углы сторон.

§ 47. СПОСОБ УСЛОВИЙ С ДОПОЛНИТЕЛЬНЫМИ НЕИЗВЕСТНЫМИ

Другим широко распространенным комбинированным способом

уравнивания является так называемый способ условий с дополнитель-

ными неизвестными, предложенный Ф. Гельмертом.

Он позволит упростить составление условных уравнений, хотя и

увеличивает их число. Это достигается путем введения в уравнения I

неизмеряемых величин, называемых дополнительными неизвестными,

при этом число условных уравнений будет равно г' — г + I.

Так, если в сети треугольников (см. рис. 70) не был измерен ка-

кой-либо угол, например у

, то, введя его как неизвестное, составим

г' = п — к + 7 = 8 — 4 + 1 = 5 условных уравнений. Дополни-

тельные неизвестные в виде поправок ориентирующих углов и коор-

динат узловых точек вводят при уравнивании полигонометрических

сетей [см. (4.67)], что упрощает вид условных уравнений.

Приведем кратко теоретические основы уравнивания этим спосо-

бом. В отличие от коррелатного способа пусть имеем исходную систему

уравнений связи числом г' = г + I

сГ

,... , К

, 1

, 2

,..., 2,) = 0;

Фг (^1» У

•••

Уп> ^2> •••

ЛУи У»....У

, 2

, ..., 2,) = 0,

(5.47)

где У

{

и 2] — истинные значения измеренных величин и неизмеряе-

мых неизвестных. Приводя уравнения (5.47) к линейному виду, полу-

чим

[сю] + [АЪг] + щ = 0;

[Щ + [58г] + щ = 0;

[8»] + [08г] + ш

<=0,

(5.48)

где, как и ранее в коррелатном способе, а^ Ь

(

, ..., — частные про-

изводные функций ф

ср

, фг> по УI и вычислены при УI = у

коэффициенты

Ъ> \

)г

г^ '

}

Величины 2

]

}

— приближенные значения неизвестных, вычис-

ляемые, как правило, по измеренным значениям у

{

. Невязки

Щ =

Я>А

(</1> У» ... , Уп> 2<°> , ... , 2<°>) .

298.

В матричной форме уравнения (5.48) можно записать таю

ВУ + рЛг + И? = 0, (5.49)

где матрицы

/а, а

... аД /А

... А

5 =

_ [ В.... В,

...0

Решая уравнение (5.49) под условием Ф = УРУ = гпш, состав-

ляем функцию Лагранжа

Ф = у

РУ — 2к

(ВУ + рДг + ы>).

Далее находим производные

— = 2V

Р — 2К

В; = — 2Д"

ЭИ дАг *

Приравнивая их нулю, получим, как и в коррелатном способе,

V = Р-г&К (5.50)

и дополнительно уравнение

/С = 0. (5.51)

Подставив уравнение (5.40) в (5.49) и объединив результат с урав-

нением (5.51), окончательно будем иметь систему уравнений

Г К =0 )

52)

с симметричной матрицей коэффициентов

^ « (р о) • <

бб3

С матрицей такого вида мы уже встречались в параметрическом

способе с условиями в предыдущем параграфе. В подробной записи

(5.53) имеет вид (при = 1).

[00]*! + [аЬ]к

+ ... + [ад]к

, + Л

8г

+Л

8г

+...+Л

8г,+ш

=0;

[аЬ]к

+ [ЬЬ] к

+ ... + [Ьд] к

, + Я

+В

+...+Я

Ц+да

=0;

Шк

+ [Ь§] к

+ ... + [

] к

, +0

8г

+...+0,82

+ш,=0;

А& + В,к

+ ... + 0,к

, =0;

+ В

+ ... + 0

, =0;

+ ' =0.

299

Общее число уравнений здесь равно 5 = г' + I = г + 21.

Решая систему (5.52) тем или иным способом, находим поправки

Й2;, коррелаты к

и далее поправки

VI = + Ь

(

+ ... + 8хк

,. (5.54)

Уравненные величины будут равны

— (0)

У1 =

Уй

+ о»: 2 = г, + 8г,.

Окончательным контролем решения задачи будут равенства

ФА(Л« Й»-. Уп>

2> г,) = 0

(при условии, когда коэффициенты системы (5.52) вычислены правиль-

но, достаточно проверить условие шн = 0, где ал, — невязки, вы-

численные по уравненным значениям у

{

и г

{

В этом способе уравнивания, так же как и в коррелатном, спра-

ведливы контрольные формулы

— \рхю] = [кхш\ = [хи

• «] = [Е

а+

, • 5],

причем ву,,

= ы)

= - 0, 2

8+1

= [ш].

Систему (5.53) можно решать в матричной форме по формулам

К = — ЛГ^Дг — ЛГЧР,

ЛГ»рд

+ р

ЛГ

№ = 0 (5.55)

или

ЯДг + Ь = 0, (5.56)

где

Я = Р

ЛГ

Р;

Из формулы (5.56) находим вектор Аг = —Ц~

Ь и далее согласно

формулам (5.55) вектор коррелат. Можно также применить формулы

(**)=-< (Г)-

б7

Оценка точности. 1. Среднюю квадратическую ошибку

единицы веса вычисляем по формуле р. = |/ 1ЕЕ11.

2. Для оценки точности уравненных неизвестных вычисляем, как

и в параметрическом способе, обратную матрицу

причем

= р

лг

р ' (5.59)

300.

является матрицей весовых коэффициентов величин г

(

. Ее можно по-

лучить в схеме Гаусса, как и в параметрическом способе (причем мат-

рицу можно не вычислять). Веса р

и р~ можно получить по

формулам вычисления весов последнего и предпоследнего неизвест-

ного.

3. Для оценки точности любой функции уравненных величин

Р — Р (У1> Уг

•••»Уп>

п)

ее приводят к линейному виду

р = т + [Ф8г1 + /о,

где

дР

дУ

Ф,=

д Р

дг1

Величина для оценки точности не нужна. Далее в схему Гаусса

добавляют столбец

Ч*а?]

[*ьп

(«г/1

( ы,

Ф,

= 1 фт

Ф«

Ф,

Обратный вес получают в виде алгоритма

/Рр- = [я/7 • 5], если

же известна обратная матрица (5.58), то применяют формулу [7]

= N.. - ЩФ)

-.т

к, г

4,7

,т

I .

(5.60)

аналогичную (4.49) при коррелатном способе.

Решим следующую задачу.

5.19. Уравнять по способу условий с дополнительными неизвестными сеть

триангуляции (см. рис. 51), если угол У* не был измерен. Исходные данные взять

из задачи 4.23.

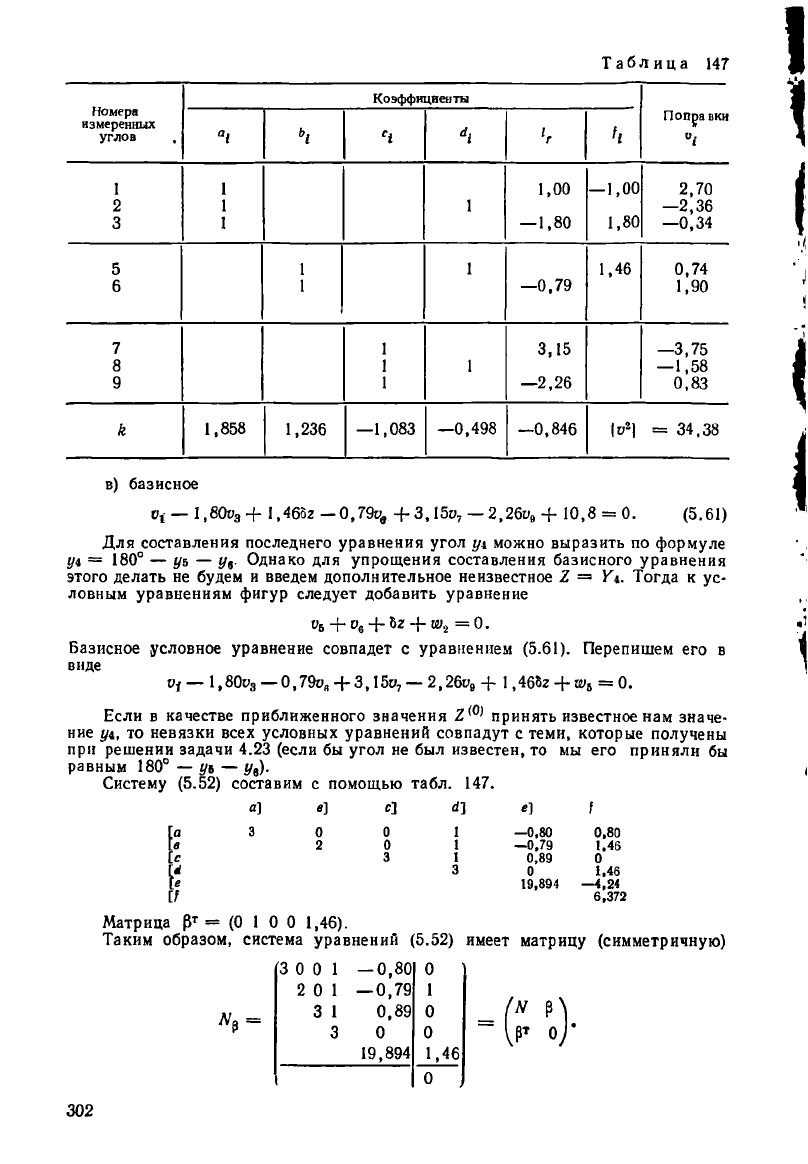
Решение. В этом построении возникают условные уравнения:

а) фигур

+ +Щ =0. + +Щ + =0;

б) жесткого угла

301.

Таблица

118

Номера

измеренных

углов

Коэффициенты

Номера

измеренных

углов

1 'г

Попра вки

1,00

—1,80

—1,00

1,80

2,70

—2,36

—0,34

-0,79

1,46

0,74

1,90

3,15

—2,26

—3,75

— 1,58

0,83

1,858

1,236

—1,083

—0,498

—0,846

= 34,38

в) базисное

VI — 1,80о

+ 1,463г -0,79о

+ 3,15о

— 2,26^ + 10,8 = 0.

(5.61)

Для составления последнего уравнения угол у± можно выразить по формуле

у4 = 180° — Уъ — Уь Однако для упрощения составления базисного уравнения

этого делать не будем и введем дополнительное неизвестное 2 = К

. Тогда к ус-

ловным уравнениям фигур следует добавить уравнение

"б+»в +

5г

'2=

Базисное условное уравнение совпадет с уравнением (5.61). Перепишем его в

виде

VI — 1,80^ — 0,79о„ + 3,15о

— 2,26ч

+ 1,4652 + щ = 0.

Если в качестве приближенного значения 2

(0>

принять известное нам значе-

ние то невязки всех условных уравнений совпадут с теми, которые получены

при решении задачи 4.23 (если бы угол не был известен, то мы его приняли бы

равным 180° — уъ — у

с помощью табл. 147.

Систему (5.52) составим

а]

с]

—0,80

—0,79

0,89

19,894

0,80

1,46

-4,24

6,372

Матрица Р

= (0 1 0 0 1,46).

Таким образом, система уравнений (5.52) имеет матрицу (симметричную)

N0 =

3 0 0

1 — 0,80

2 0 1 — 0,79 1

3 1

0,89 0

3 0 0

19,894

1,46

= Го)-

302

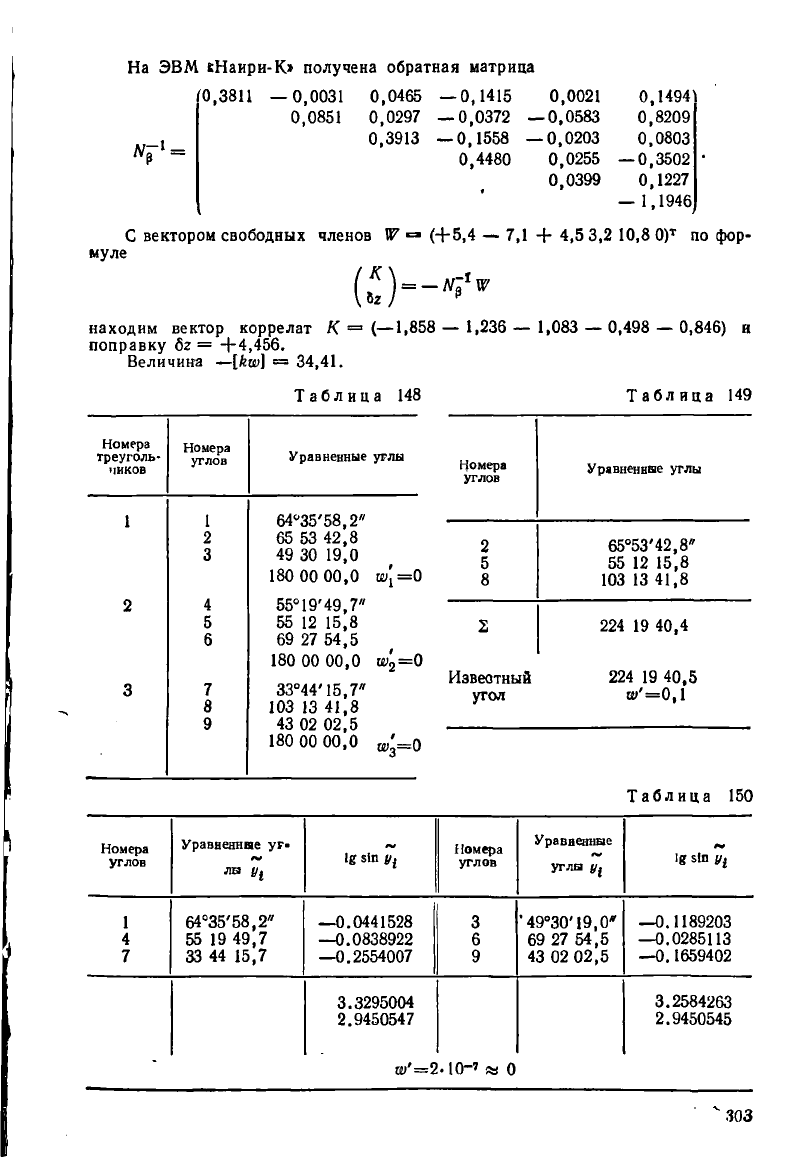
На ЭВМ кНаири-К» получена обратная матрица

10,3811 —0,0031 0,0465 — 0,1415 0,0021

0,0851 0,0297 —0,0372 —0,0583

0,3913 — 0,1558 — 0,0203

0,4480 0,0255

0,0399

0,1494

0,8209

0,0803

— 0,3502

0,1227

— 1,1946

муле

С вектором свободных членов И7 (+5,4 — 7,1 + 4,5 3,2 10,8 0)

по фор-

находим вектор коррелат К = (—1,858 — 1,236 — 1,083 — 0,498 — 0,846) и

поправку 8г = +4,456.

Величина —[кии] = 34,41.

Таблица 148 Таблица 149

Уравненные углы

64°35'58,2"

65 53 42,8

49 30 19,0

180 00 00,0 ш[=0

55° 19'49,7"

55 12 15,8

69 27 54,5

180

00 00,0 щ=0

33°44'15,7"

103 13 41,8

43 02 02,5

180 00 00,0 „'-о

Номера

Уравненное углы Уравненное углы

65°53'42,8"

55 12 15,8

8 103 13 41,8

224 19 40,4

Известный

224 19 40,5

угол ш'=0,1

Таблица 150

Номера

углов

Уравненные уг-

лв у

1В »1п VI

Номера

углов

Уравненные

углы у

А*

1(Г

|п у

64°35'58,2"

55 19 49,7

33 44 15,7

—0.0441528

—0.0838922

—0.2554007

•49°30'19,0"

69 27 54,5

43 02 02,5

—0.1189203

—0.0285113

—0.1659402

3.3295004

2.9450547

3.2584263

2.9450545

ш'=2-10» 0

"303