Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений

Подождите немного. Документ загружается.

Поправки VI вычислены в табл. 147 по формуле (5.54). В табл. 148 вычисля-

ем уравненные углы и остаточные невязки треугольников*. В табл. 149 и

150 вычислены остаточные невязки условий известного угла и базисного.

Оценка точности. 1. Средняя квадратическая ошибка измерения

одного

2. По формуле (5.60), учитывая, что

N<=(0,80 1,46 0 1,46 —4,24), Ф = —1,46,

находим

цепка 1 и Ч Н ц 1 Л. 1. ч^я

угла т = 2,9".

(Л^ = (—0,133 —0,884 0,019 0,857 —0,394 2,031) X

1 /

~ = (—

440

> =

372

440

812

Далее вычисляем

1е5

=^2,9 |/7,812 =8,1 (ед. 6-го знака логарифма)

от,, _

1 _ 8,1 _ 1

з М 0,43-10

53000

(в задаче 4.23 получено /л

/а = 1/61 000).

3. Средняя квадратическая ошибка неизвестного г (угла

= 2,9 У 1,195 = 3,2"

У4

(величина 1,195 есть взятый со знаком «+» последний диагональный элемент

матрицы Л^

что

следует из (5.58).

5.20. В предыдущей задаче решить систему уравнений (5.52) и выполнить

оценку точности функций по схеме Гаусса и методом квадратных корней.

5.21. Выполнить уравнивание по способу условий с дополнительными неиз-

вестными в условиях задач 4.23, 4.26 и 4.27, приняв соответственно неизмерен-

ными углы </„, у

, у

Способ условий с дополнительными неизвестными применяют для уравни-

вания геодезических сетей при наличии в измерениях систематических ошибок,

которые вводят как дополнительные неизвестные [при параметрическом способе

уравнивания их также вводят в качестве неизвестных (см. § 33)].

Так, например, полагая, что в условиях задачи 4.23 каждый угол был отя-

гощен постоянной систематической неизвестной нам ошибкой с, получим услов-

ные уравнения

+ + ?

+ = 0;

ч + о» + +

° + = о;

о, + «

+ о

+ ?б + = 0; (5.62)

5 + Зо + щ = 0;

VI — 1,80о

+ 1,46^4 — 0,79ц, + 3,15и,— 2,26у

+ 0,76с + го

= 0.

* Измеренные углы ух и г

(0)

= приведены в табл. 150.

304

Допустим, что измеренные углы получены равными у

{

+ с, где с = 1", а у

{

при-

ведены в задаче 4.23. Тогда будем иметь новые невязки

0)1

= 5,4 + 3,0 = 8,4;

и>

= -7,Г+3,0 = -4,1;

^3 = 4,5 + 3,0 = 7,5;

что следует из уравнений (5.62).

Как и в задаче 4.21, получим матрицу

щ = 3,2 + 3,0 = 6,2;

= 10,8 + 0,7= 11,5,

Матрица Р = (3 3 3 3 0,76), что также следует из системы (5.62).

Обращая матрицу

О/

на ЭВМ «Наири-К», получим матрицу

[0,2801 —0,0583 — 0,0591 —0,1653 0,0105

+ 0,2811 —0,0513 — 0,1682 — 0,0124

0,2932 — 0,1687

0,5008

-1

N. =

— 0,0159

0,0059

0,0468

0,1111

— 0,1111

) = — (— 1,243 + 3,211 —0,611 — 1,208 — 0,590— 1,

310)

Далее вычисляем вектор

По формуле (5.54) находим поправки

о = (— 1,83 — 2,45 — 0,18 2,35 2,00 3,67 — 2,47 — 1,82 + 0,72)

Уравненные значения углов будут

У1=У1+Щ + ~г-

Следовательно, при уравнивании триангуляции постоянная систематическая

ошибка полностью погашается. Этот вывод можно получить и теоретическим пу-

тем.

Заметим, что вычисленная величина с — —1,3" оказалась достаточно близ-

кой к с = 1" даже при небольшом числе избыточных измерений.

Оценка точности. 1. Величина [то] = —[ки/] = 42,40. Средняя

г = п — к = 4,

квадратическая ошибка т = ^/^^2,40 _ з

Де

сь

так как к = 4 + 1 = 5.

Отметим, что если величины

"у

получены не искаженными систематическим

влиянием, то средняя квадратическая ошибка т

искажена максимально и ха-

рактеризует не точность самих измерений в смысле оценки дисперсии О =

= М[(Х — Мх)

], а точность результатов измерений относительно их истинных

305.

•значений, т. е. И = М[(Х — Х

ист

)

]. Поэтому можно написать т

= т

+ с

откуда

—? = 10,6— 1,72 = 8,88"; т = 3,0".

Напомним, что в задаче (4.2) получено т = 2,9'".

2. Средняя квадратическая ошибка т

= 3,0''У 0,111 =• 0,99".

3. Как и в предыдущей задаче, найдем р^г. При этом

Щ= (0,80 0 0 1,46 — 6,372);

Ф = [/]= +0,80; % = 8,503.

Согласно формуле (5.60) вычисляем

(Щ Ф) Л^

^^ = (0,005 —0,047 —0,103 0,331 —0,281 0) = 2,279;

— = 8,503 — 2,279 = 6,224.

Далее т? = /п, = 3,0 /6,224 = 7,48 и

7-48 1_

з ~~ 0,43-10

е _

57 000 '

5.22. Решить систему (5.62) по системе Гаусса с оценкой точности функции

« величины с.

5.23. Уравнять по одному из вариантов задач 4.23, 4.26, 4.27 углы, исказив

•их систематической ошибкой по указанию преподавателя.

§ 48. УРАВНИВАНИЕ КОРРЕЛИРОВАННЫХ ИЗМЕРЕНИЙ

Результаты непосредственных измерений чаще всего являются не-

коррелированными величинами. Но в математическую обработку мо-

гут включаться не сами измерения, а их функции, например углы,

вычисленные по независимо измеренным направлениям, предвари-

тельно уравненные измерения или их функции, например дирекци-

онные углы сторон, приращения координат и др. Поэтому возникает

задача уравнивания коррелированных измерений. Во всех этих слу-

чаях необходимо знать матрицы их обратных весов <Э или весов р,

которые в отличие от случая некоррелированных измерений уже не

будут диагональными. Метод наименьших кадров в применении к не-

коррелированным измерениям называют классическим, а к коррели-

рованным — обобщенным.

При уравнивании коррелированных измерений необходимо при-

менять матричную форму записей и вычислений. Так, параметриче-

ский способ сводится к составлению нормальных уравнений

КАх +6 = 0, (5.63)

где матрицы равны

К = А

РА, (5.64)

"306

Ь = А

РЬ.

(5.65>

Лемма Гаусса имеет вид А

РУ = 0.

В коррелатном способе имеем матричное нормальное уравнение

+ № = 0, (5.66)

N = В(}В

, (5.67)

V = (2Я

/С. (5.68)

Как видим, основные формулы в матричной записи те же, что и в

классическом способе уравнивания, с той лишь разницей, что матрица

Р недиагональная. Поэтому все алгоритмы Гаусса, включающие вес,

уже не имеют места. Они могут быть сохранены условно лишь о

| целью решения системы нормальных уравнений в схеме Гаусса и

метода квадратных корней.

Легко заметить, что применение параметрического способа урав-

нивания требует знания матрицы Р, а коррелатного —

С?

= Р'

. По-

этому выбор способа зависит от того, какая матрица имеется: Р или

Я-

Таблица 151

Номера измерений

Номера

углов

! 2

4 5

—0,5

Таблица 152

Номера

урав-

нений

Номера измерений

Номера

урав-

нений 1 2 3 4

5 6

8 9

1,00

—1,80

1,46

—0,79

+3,15

—2,26

—1,00

1,80

—1,46 1,46

где

и вектор поправок

307.

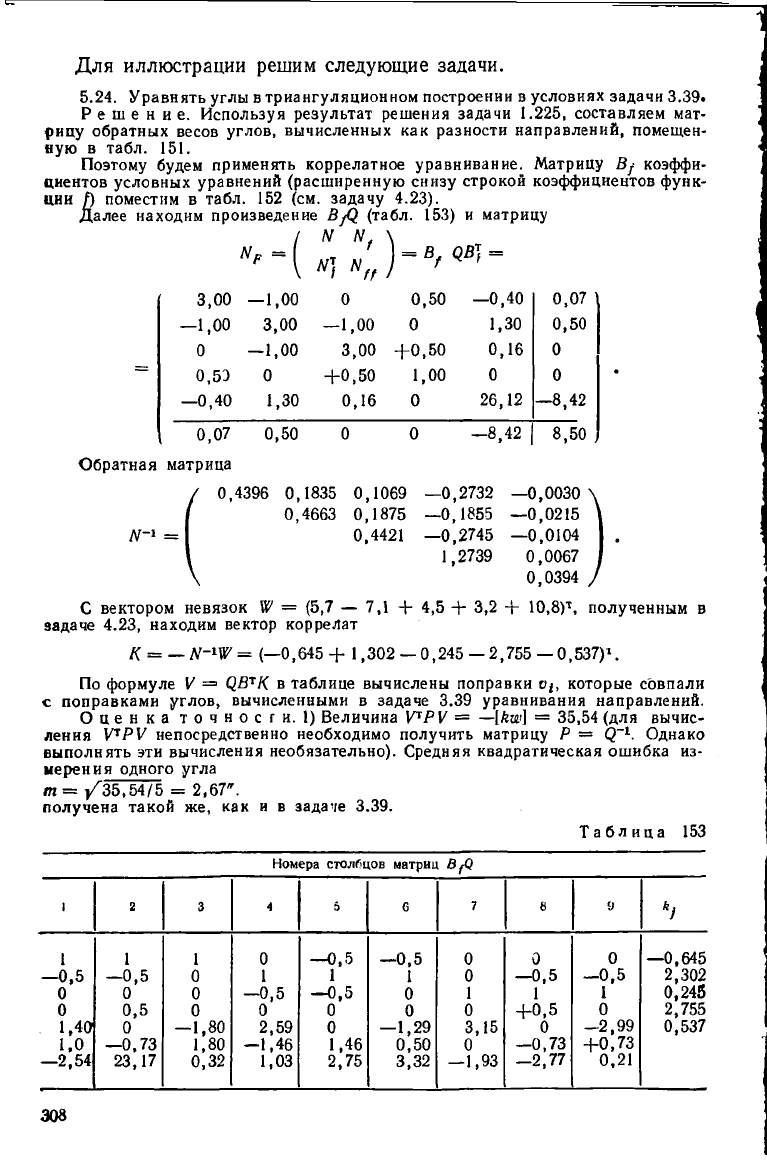
Для иллюстрации решим следующие задачи.

5.24. Уравнять углы в триангуляционном построении в условиях задачи 3.39.

Решение. Используя результат решения задачи 1.225, составляем мат-

рицу обратных весов углов, вычисленных как разности направлений, помещен-

ную в табл. 151.

Поэтому будем применять коррелатное уравнивание. Матрицу В{ коэффи-

циентов условных уравнений (расширенную снизу строкой коэффициентов функ-

ции /) поместим в табл. 152 (см. задачу 4.23).

Далее находим произведение В/2 (табл. 153) и матрицу

N N ^

N. =

= в

ОВ] =

3,00 —1,00

0 0,50

—0,40

0,07

—1,00 3,00 —1,00 0

1,30

0,50

—1,00

3,00 +0,50 0,16 0

—

0,5Э 0 +0,50

1,00

—0,40 1,30 0,16 0

26,12

—8,42

0,07

0,50

0 0

—8,42

8,50

Обратная

матрица

0,4396 0,1835 0,1069 —0,2732

0,4663 0,1875 —0,1855

0,4421 —0,2745

1.2739

полученным в

—0,0030

—0,0215

#-•=

0,4421 —0.2745 —0,0104

0,0067

0,0394

С вектором невязок № = (5,7 — 7,1 + 4,5 + 3,2 + 10,8)\

задаче 4.23, находим вектор коррелат

К = — (—0,645 + 1,302 — 0,245 — 2,755 — 0,537)\

По формуле V = О.В^К в таблице вычислены поправки о/, которые совпали

с поправками углов, вычисленными в задаче 3.39 уравнивания направлений.

Оценка точности. 1) Величина У*РУ = —[А®] = 35,54 (для вычис-

ления УРУ непосредственно необходимо получить матрицу Р = С

-1

. Однако

выполнять эти вычисления необязательно). Средняя квадратическая ошибка из-

мерен

яодного угла

т = /35,54/5 = 2,67".

получена такой же, как и в задаче 3.39.

Таблица 153

Номера столбцов матриц

4 5

8 9

1 1 0

-0,5

—0,5 0 0

—0,645

—0,5 —0,5 0 1

—0,5

2,302

0 —0,5

—0,5

1 0,245

0,5

0 0

+0,5 0

2,755

1,40 0 —1,80 2,59 0

—1,29 3,15 0

-2,99

0,537

1.0

—0,73 1,80

-1,46

1,46 0,50

-0,73

+0,73

—2,54 23,17

0,32 1,03 2,75 3,32 —1,93

—2,77

0,21

308.

2) По формуле

1 //>_ = N ,,—N1 ,

р //

находим обратный вес функции.

Величина

= (0,149 0,427 0,189 —0,168 —0,342)^=3,103

и 1/Р~=8,50 —3,10 = 5,40; «1^ = 2,67 ]/5/Й) = 6,18.

Так как 8 = 1524, то

6,18

0,43-10

« = 0,022 м (в задаче 3.39 т

= 0,021 м).

5.25. Выполнить окончательное уравнивание дирекционных углов в сети

триангуляции, приняв их уравненные в задаче 3.27 (только за угловые условия)

значения в качестве непосредственно измеренных.

Решение. Матрица коэффициентов нормальных уравнений К, получен-

ная в задаче 3.27, представляет матрицу весов предварительно уравненных ди-

рекционных углов, т. е.

Ра = Л= • (5.69)

Для любой сети триангуляции ее можно составить по формулам: а) для

диагональных элементов [7]

(Ра) л = п

}

где П/ — число углов, имеющих одну из сторон с номером /:

б) для недиагональных

(Я

)у

= -1,

если между сторонами / и Л измерен угол. Все остальные элементы равны нулю.

Применяя параметрический способ уравнивания, составляем уравнения по-

правок для дирекционных углов сторон с матрицей коэффициентов

А = •10?

и вектором свободных членов Ь с элементами Ц = а*®' — а

Ь = (—0,1 —2,7 +1,1 +2,2 +2,6)

(см. задачи 3.38, 3.37 и 3.27).

Далее находим матрицу

0,482

4,162

А= | —1,402 2

•

—1,150

309.

и далее матрицы

К = Л

Л =

и вектор

А^РЬ = (—15,358 -5,910 10,153 — 8,014)*. 10

совпадающие с полученными в задаче 3.38. Далее, как и в задаче 3.38, находим

вектор поправок координат пунктов

Д* = (1,92 0,89 —1,57 0,87)*. К)-

поправок дирекционных углов

= ААх + I =

и уравненных дирекционных углов

01 = 229°30'17,9" +0,9» = 229°30'18,8";

а.

= 294 06 17,4 + 0,2 = 294 06 17,6;

183

34 12,7 + 0,9=

183

34 13,6;

= 238 54 00,7 + 0,1" = 238 54 00,8;

= 281 56 01,2 — 0,4 = 281 56 00,8

(предварительно уравненные дирекционные углы взяты из задачи 3.27).

По формуле Ф= УРУ находим квадратичную форму У

= 43,16 и

выполняем контроль

К РаУа = ^Р^ + &

х-А

Ь = 43,16.

Все дальнейшие вычисления выполняются так же, как и в задаче 3.38.

Заметим, что в задаче 3.50 вместо матрицы Р

(5.69) была принята диаго-

нальная матрица Р

= {2 4 2 4 2} и получены приближенно уравненные ди-

рекционные углы

<*!•

= 229°30'18,6"; а

= 238°54'00,2";

= 294°06'17,2"; а

= 281°56'01,2".

= 183°34'13,3";

Во многих случаях пренебрежение зависимостью приводит к более сущест-

венным искажениям.

В задаче 5.13 по существу выполнено коррелатное уравнивание дирекцион-

ных углов с использованием матрицы (2 = Р~

Если предварительно уравненные дирекционные углы сторон получают по

измеренным направлениям, то матрицу Ра составляют по формулам [7]:

а) для диагональных элементов (Р

)]]= О/— 11$

ктч

— 1/5й

кон

, где б

- = 1

или 2 соответственно для односторонних или сплошных направлений, 5#

нач

*кон

—

соответственно числа направлений, измеренных на начальном и конеч-

ном пунктах ке/;

310.

б) для недиагональных элементов (Р

)у

•= —1/5^

, где в

ке/ н

— число

направлений, измеренных на пункте к, общем для сторон ] и к.

Так, для сети (см. рис. 57) матрица

1,167 —0,333 —0,333 0 0

1,417 —0,333 —0,250 0

1,333 —0,333 —0,333 | . (5.70)

1,417 —0,333

1,167

Вектор свободных членов в системе нормальных уравнений при предвари-

тельном уравнивании углов

= 0

имеет составляющие 6у = /у + /у, где /у и /у — свободные члены уравнений по-

правок прямых и обратных направлений, измеренных по стороне

5.26. Выполнить уравнивание измеренных направлений в условиях задачи

3.39, применяя описанный двухгрупповой параметрический способ [матрица

имеет вид (5.70)].

Матрица К = А

А имеет вид

4,6092 3,8633 —2,9178 3,4733'

6,4760 —4,1005 4,3783

^ 3,9042 —3,2622

4,3295

Обратная матрица Ф = совпадает с матрицей полученной в табл. 73

задачи 3.39.

В заключение приведем формулы для обработки многократных

коррелированных измерений одной и той же величины. При этом урав-

нивания поправок имеют вид V = А8х + Ь, где матрица

(5.71)

вектор

причем 1, = х<

>—у

Если в качестве приближенного значения *

(0)

принять тт то

по обозначениям § 25

(5-72)

Нормальное уравнение будет

РЬх + А

РЬ = 0, (5.73)

где Я = А

РА.

311.

Учитывая выражение матрицы (5.71), найдем, что Я — 2

, где

через 2

обозначена сумма всех элементов матрицы Р. Для вектора

свободных членов Ь = А

РЬ получим, учитывая обозначение (5.72),

выражение

]рЬ

1=1

где [р] I — сумма элементов /-го столбца матрицы Р.

Решая уравнение (5.73), находим поправку

= ШШ. „

2 м

х=

<о>+Ы-

(574)

"р

В частном случае, когда матрица Р диагональная,

- (0) , [ре]

X = X + -

- '

[р]

Выражение (5.74) представляет собой обобщенную арифметическую

средину.

Заметим, что если л:

> = 0, то

х =

2 [р]|*1

1=1

Величина 2

есть вес обобщенной арифметической средины. Сред-

ние квадратические ошибки

Г УРУ

^=т

, а т =

6.27. С помощью таблиц нормально распределенных случайных чисел Iу

сделать выборку объема к = 10. Вычислить разности

'з — 'а I

'п — 'п.-1

и затем найти обобщенную арифметическую средину из величин = + с,

где с — заданная постоянная величина и ошибки ц и пг—.

Указание: матрица (см. задачу 2.24)

/я—

л —2 п — 3 ... 1\

_2_( 2 (л — 2) 2(я —3).,. 2

\ л-1,

а величины

п(я

— 1)

Вычисления удобно оформлять в табл. 154, приводимой для одного из вариантов

при к = 6 (с = 10).

312.

[Р)1

= /(п-0-

Таблица

118

'у

1 Р]

1 0,200

0,992 10,992

5 1,2915

1,192 — 1,200 8,800

—0,9005

—0,008

+0,043

10,043

9 0,3425

0,035

+1,007 11,007

8 1,3065

1,042 —2,857

7,143

—2,5575

6 —1,815

—2,857

7,143 —2,5575

В результате вычислений получено:

X [рЪ*/ = 339,519, Е-= 35

|РЬ

*'" 339,519

* = ; = ^ = 9,7005

поправки VI = х —

Контроль: А

РУ = 2 =0,0005 да 0.

1=1

Так как матрица

/5 4 3 21

. / 4 8 6 4 2

Р = — I 3 6 9 6 3

I 2 4 6 8 4

\1 2 3 4 5,

то IАЯ= (1,313 0,043 0,574 0,419 — 2,347) и Iпру = 8,403.'

Эту величину можно проконтролировать по формуле

РУ = иРЬ + В* • А

РЬ = е

Ре + 8* • А

РЬ.

Но А

РЬ = —2рбдс, поэтому

УРУ = е

Ре — 8х

- е^Ре — ^

5 \ 2

'•=} !_

[р«]'

(формула, аналогичная [рт] = [р// • к\ =а [ре*] — О! в случае некоррелиро-

ванных измерений). Если же *

(0)

= 0, е^ = то

утру = X

Рх

[РЬ *1 '

313