Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений

Подождите немного. Документ загружается.

с |,в;>ДР«

Г1|Ч,,0ГО

- Контрольные значения З^

*. 2з

\ и т. д. пи-

ЦУДЛ

пс

™пнештют. Исключение в эгом отношении составляет

только величина в параметрическом способе.

4. Значения неизвестных находят ири помощи элимпнациоииых

строк Е

, Ео и Е Для выделения этих строк их обычно заполняют

другими чернилами п ниже этих строк делают пропуск.

Нижнюю часть схемы, в которой вычисляют значения неизвест-

ных, принято называть «горкой».

5. В коэффициентах элпминациошшх строк сохраняют обычно

на одпн-два десятичных знаки больше, чем в остальных строках.

В табл. 33 приведен пример решения четырех нормальных урав-

нений по схеме Гаусса — Дулитля на логарифмической линейке.

Задана система уравнений п суммы 2

3.00т, +0 39то—0,28т

-0.2Ст

+3.36=0; 2,=+6.21;

+0.39Т! + 2,

.3т

0,20т

- 0.1 Тт.!

^=0; 2, = +6.20:

—0,28^ + 0,20^+108т

+0,29т,-2

- 0; 2з= -133:

—0.2Ст,—0,17т

+0,29тз + +2{9П

=»0;

«+4.45;

|^Л = 3568; 2

42.75

«*[/>/*].

Для окончательного контроля вычислении подставим пайденпые

неизвестные в суммарное уравпенпе для чего вычпелпм его коэффи-

циенты п свободный член (см. формулу VI.30),

=+6

-3 36=+2.85:

- Ц= +63 -

3.34

= +2,<15;

2з-А

=-Ш (-2.62=+! 20:

2 л -

Л.1

= +4,45 -

2,09

= +1.46;

- [рИ\ =+42 75-35.68= +7.07.

Теперь получим

-2,85

- 0,85 — 2.05 •

1,65+ 1.29

•

3.28-1.46

• 2.78

7.07

= -2.42-4.87+4 2-3-

4.06

+ 7.07=—0.05.

Остаточная погрешность нрепебрегаемо мала.

2. Сокращенная схема для вычислений

на настольной вычислительной машине ЭВМ

При вычислениях на арифмометре коэффициенты преобразован-

ных уравнений, являющиеся суммами коэффициентов уравпеппй (/V)

п произведений двух мпожптелей, можно получать сразу на арифмо-

метре без промежуточных записей. Тогда в схему решения пужпо

выппсывпть только коэффициенты основных, преобразованных^

злиминацнонных уравнений.

Все

произведения чисел элпмннациониых

строк па чпела вышестоящих строк (т. е. Е

* Е^Х, Е

ЛГ<»> и

. п.)

233

выннсывлть но сл еду от. Так жо без промежуточных записей можно

получить п неизвестные.

Точность вычислении но арифмометре указанным способом зна-

чительно повышается но сравнению с вычислениями па логарифми-

ческой линейке, тлк как. во-иервых. на арифмометре вычисления

можно производить с большим чне.иом десятичных знаков, и, во-вто-

рых, совсем не будут влиять ошибки округлении промежуточных

результатов.

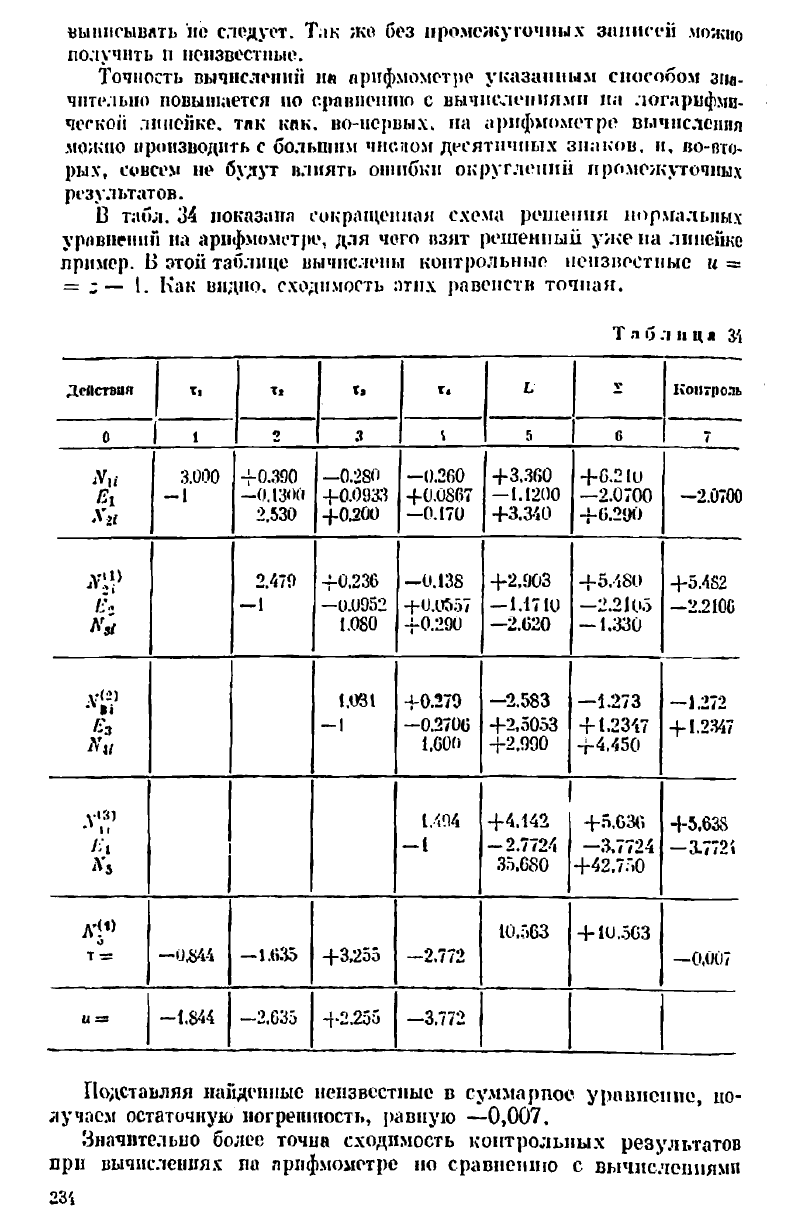
13 табл. 34 показана сокращенная схема решения нормальных

уравнении на арифмометре, для чего взят решенный ужена линейке

пример. 13

этой

таблице вычислены контрольные неизвестные м =

= ;

—

1. Как видно, сходимость птнх равенств точная.

Т я б л и

ц ж

Действия т» X, Т|

Контроль

Я 1

Уи

Рп

ХЦ

3.000

-1

-г 0.390

2.530

-0.280

+0.0933

+0.200

-0.260

+0.0867

-0.170

+3.360

— 1.1200

+3.3-10

+0.2

—2.0700

+6.2УО

-2.0700

2.479

-1

+0.236

—11.0952

1.080

-0.138

+О.Ц557

+0.290

+2,903

-1.1710

—2.620

+5.480

-2.2105

—

1.330

+5.482

-2.2 ЮС

Ь'и

1.031

-1

+0.279

-0.2706

1,(ИК>

-2.583

+2,5053

+2.900

—1.273

+ 1.2347

+4.450

-1.272

1.2347

1:1

Л'з

1,104

-1

+4.142

-2.7724

35.680

+п,СЗ«

-3.7724

+42.7Л0

4-5,638

-3.772'.

л1«

—

-0,844 —1.635 +3,255

-2.772

10,563

+111.503

—0,007

и =

—1.844 -2.035 +2.255

-3.772

Подставляя найденные неизвестные в суммарпое уравнение, по-

лучаем остаточную погрешность, равную —0,007,

Значительно более точна сходимость контрольных результатов

при вычислениях па арифмометре но сравнению с вычислениями

23',

на логарифмической линейке. Это преимущество арифмометра вы-

является тем больше, чем Польше число уравнений.

Однако логарифмическая линейна очень часто вполне обеспечи-

вает практически необходимую точность.

§ 64. СПОСОБ КРАКОВЯНОВ

Для последовательного исключения неизвестных при работе

с НСМ аффективен способ крлковииов. разработанный польским

астрономом Р»апахевичем *. Принтом способе в наибольшей степени

используют возможности арифмометра; наименьшим образом влияют

ошибки округлений; вычисления укладываются в весьма компакт-

ную схему.

Сущность способа заключается в том. чгп на арифмометре или

другой вычислительной машине такого шна получают без проме-

жуточных записей коэффициенты уравнении эквивалентной системы,

деленные на корень квадратный из квадратичных коэффициентов

этих уравнений. Соответствующие строки нчзовем «краковяновыми».

Нетрудно убедиться в том, что произведения элементов элпмипа-

ннопиых уравнений на элементы эквивалентных уравнении, которые

(произведения) суммируют в процессе преобразований в алгоритме

Гаусса, равны произведениям чисел краковяновых строк, стоящих

в тех же графах.

Покажем в гауссовых обозначениях решение трех уравнений спо-

собом краковяиов.

Схема решения приведена в табл. 35, в которой буквами К обо-

значены краковянорые строки.

Для удобства вычислений все величины строк Д" (т. е. основных

уравнений), кроме квадратичных коэффициентов, выписывают в схе-

му с обратными знаками.

Порядок получения строки К

в пояснениях ие нуждается;

получают на лрифмомегре следующим образом.

Взяв на логарифмической линейке нчн по таблицам приближен-

ное значение корня (до 3—значащих цифр), ставят его на рычагах

и делят па него величину Л

: искомое значение корня будет равпо

среднему арифметическому нз полученного частного и делителя.

Иными словами, корень получаю! но формуле

- агр-}-а/г,)

1 «,= 2 '

где х

— приближенное значение корпя.

Заметим также, что остальные величины строки К

выгоднее

вычислять на арифмометре по обычным делением, а способом

у м н о ж е н л я.

* Советским геодезистам способ краковяиов известен еще как способ

квадратных к о р п с й, а также как сиособ Холоцкого. Прио-

ритет способа принадлежит Холецкому, однако Баиахсштч получил этот сиособ

как частный случай разработанного нм краковянового исчисления.

Таблица 35

Дсйствпл

ДГ-,

ЛЧ

-V»

Л',,-

Неиз-

вестные

Г Л',

— ЛГ,2

Ум?

Контроль

—Л'

1 Л'п

У®

— /,«

—

-/-Я

I РЧ)

-1л

1 к

VI* п

"2!

То

-/Л»

Ул^У

УЛГ

•"о

7Щ

-а

' зз

Величина Л'зУ получается как разность

-Л*.

'11

'"-ЧтМ

или, в обозначениях схемы, Л

— К12 (нрн установке па арифмо-

метре величины Л

„» нужно, конечно, учитывать число десятичных

знаков квадрата величины = Нетрудно видеть, что

V Л'и )

в результате будет подучена величина

(

Л>=Л\

Л"|«Л

12'* К

Не енпмая полученной величины Л'^У с каретки арифмометра

извлекают из нее корепь описанным выше способом и результа-

выписывают в строку /С

2г

Числители дробей строки К

гх

вычисляют по формулам

—Уз

~'—-^23 Ч"

—

Л ае

—

+К

Кц.

Величины к, и Ькг получают как сумму влево располож

пых чисел, придавая крайнему слева числ^ зпак минус.

236

Зпачеппе Л 33 ил ходят по формуле

Перед извлечением корпя нз нслпчшш ее (а вообще — кввдра-

тнчиын коэффициент последнего уравнения якпивалептпои системы)

выписывают внизу в графе «Л», я строке «Непзлсстныс». как попа-

за но в табл. 35. Так же поступают п с величиной — общем

случае с величиной — Л*"

Числители строки А'

получают по формулам

——1>з~1- А'мА'ц-* Л^з/^о}.'

—2з

=- —2)

+Л*|-Л*|.» - Л*8зЛ'

Вычисление всех значений краковяиовых строп, включая извле-

чение корпя и деление на ,, У АIV " пр.. выполняют

на арифмометре без промежуточных зиппсеи. Так. получив но арпф-

мометрс су.мяу —Ч~ К к К^К^,

пе

снимая с каретки,

сразу делят ее на величину выппсаппую ранее слева в стро-

ке А.*з,-. В схему вычислений выписывают лишь окончательные ре-

зультаты.

По аналогичным правилам получают величины

л^-ДО-лй-лг!,-*!,;

= -!,-{-

А'и

Л,5+/Г-, А'

-Ь

А'

,Л'

Заметим следующие различия. При получении первых слепа вели-

чин краковяиовых строк от величин строк N вы ч и

а ю

лвал-

раты чисел краковяиовых строк; /три вычислении же остальных

величии краксвяпевых строк числа верхней части таблицы а л г е -

б р а и ч е с к п суммируют с произведениями чисел к/лт-

ковяновых строк.

Контроль но строкам К такой нее, как и гго строкадг эквивалент-

ных уравнений в схеме Гаусса — Дул п тля, если брать первые слева

числа со зиаком млпус

(птмт

числа в схеме всегда положительны).

Последнее неизвестное (в нашелг примере т

) по лучают по обыч-

ной формуле

-4

а в общем случае

237

Остальные неизвестные получают на арифмометре без промину,

точных записей нрн помощи краковяновых строк но формулам

А*.»

А"«з

УМ?

А'ц

ДУчТз-Ь

К 12

т. е. почти так же. кик в схеме Гаусса — Дулитля из элиминациом-

ных строк; здесь добавляется лишь деление па корпн из квадратичиых

коэффициентов.

В табл. 36 приведен пример решения четырех нормальных урав-

нении способом краковяиов. Взята ранее дважды решенная система

уравнений. Напомним, что все величины этой системы, кроме квад-

ратичных коэффициентов, выписывают в схему с обратными зна-

ками.

Таблица ЗС

Действия

т»

х»

Тэ Г

К онтроль

С 7

х,

Л'4

А*

3,00

-0,39

2,53

+0,28

-0,20

1,08

+0,20

+0,17

-0,29

1,60

-3,36

-3,34

+2.62

-2,99

35,68

—6,21

-6,29

+1,33

-4,45

—42,75

К,

к,

1,732

-0,225

1,575

+0,162

-0,150

1,010

+0,150

+0,087

-0,274

1,223

-1,940

-1,843

+2,542

-3,383

10,613

—3,585

-3,481

+1,252

-4,606

10,615

—3,585

-3,482

+1,251

—4,606

Неиз-

вестные

-0,844

-1,632

+3,248

-2,768=

-4,138

1,495

-0,001

При подстановке найденных неизвестных в суммарное уравнение

получена остаточная погрешность, равняя всего —0,001.

Несмотря на то что в краковяновых строках сохранено на один

десятичный зпак меньше, чем в элпминацнонпых строках табл. 34.

сходимость контрольных результатов при решении способом крако-

вяков, как видим, не хуже, чем при решонип алгоритмом Гаусса

па арифмометре. При одинаковом числе десятичных знаков ошибки

округлений в способе краковяиов будут влиять на точность резуль-

татов в среднем меньше, чем в алгоритме Гаусса. Это объясняется

тем, что числа элиминационпых строк по абсолютной величине, как

238

правило, меньше соответствующих чисел краковяновых строк *,

а следовательно, и относительные ошибки округлении алимшкщион-

них коэффициентов больше ошибок соответствующих коэффициентов

краковяновых строк. Поэтому ошибки округлений сумм нронзведе-

внй. которые и являются главным источником ошибок при решении

нормальных уравнении, в способе краковяиов. как правило, метане

(при одинаковом числе десятичных знаков).

Особенно эффективен способ крчкопянон для вычислений на

ЭВМ. так как в этом способе почти в два раза меиыис промежуточ-

ной информации, чем в алгоритме Гаусса (две строки заменяются

одной).

Заметим, что \ри

\ в табл. 30 вычислено как \р11] минус сумма

квадратов краковяновых строк, т. е.

([/>/*]

=35.08).

Отметим еще, что определитель системы в табл. 36 вычисляют

но формуле

Я = А* И

•

А'Ц

•

А'ЗЗ

•

А'*,.

§ 66. РЕШЕНИЕ УРАВНЕНИЙ

СПОСОБОМ ПРОСТОЙ ИТЕРАЦИИ

Небольшие и хорошо обусловленные системы уравпешш (до 20—

30 уравнений) выгодно решат!, способом простой итерации (способ

Гаусса — Зейделя).

Последовательность действия в атом способе такова:

1. Каждое неизвестное выражают через остальные, пользуясь для

этого тем уравнопнем. в которое определяемое, неизвестное входит

с квадратичным коэффициентом. Для трех уравнении имеем

Л',2

Л'|*

1.1

-»- Л'„

2« —

V -3

х»

Л'

Л'ГЗ

Л.

-2 у„„

V ~

Л 22

•V,*

Л'»

1 —

Л 23

«^33

Л'зз

Эти уравнения назовем итерационными.

2. В процессе итерации (приближений) пил уча ют очередное зна-

чение каждого неизвестного путем подстановки последних значений

остальных неизвестных в соответствующее итерационное уравнение.

В первом приближении при нахождении г

значения г., и :

, а нрп

нахождении г

Значение г

принимают равными нулю.

Сходимость указанного процесса итерации доказана в § 75.

* Квадратичные коэффициенты урапнешш почти всегда больше единицы.

230

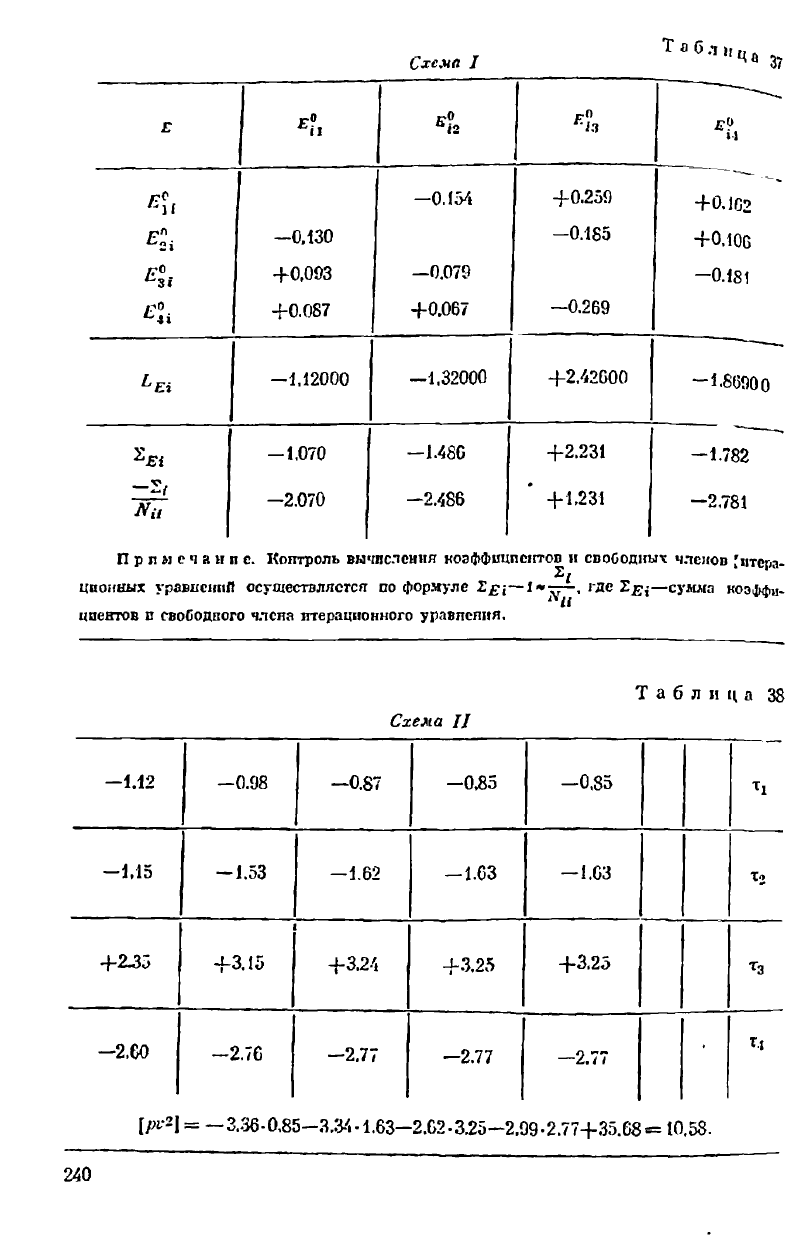
Схема I

г-0

л?

р0

'-11

-0.130

+0,093

+0.087

—0.154

—0.079

+0,067

+0.259

-0.185

—0.269

+0.1С2

+0.106

-0.181

*«

-1.12000

—1,32000 +2.42600

-1.86900

—1.070

-1.486

+2.231

-1.782

Яи

-2.070

-2.486

+ 1,231

-2,781

Примечание. Коптроль вычисления коэффициентов и свободных членов Гитера-

цпонных уравнения осуществляется по формуле ——, где —сумма коэффи-

циентов п свободного члена итерационного уравнения.

Таблица 38

Схема Ц

—1.12

-0.98

—0.87

—0,85

-1,15

-1.53

-1.62 -1.63

—1.63

То

+2^5

+3.15

+3.24

+3.25

+3,25

-2,60

-2.76

-2.77

—2.77

-2.77

•

[ре Ц = —3.36-0,85—3.34-1.63—2.62-3.25—2.99-2.77+35.68 = 10,58.

240

Вычисления выполняют при иомощи диух гх»*м. располагаемых на

двух листах бумаги.

В первую схему (табл. 37) выписывают коэффициенты и свобод-

ные члены правых частей итерационных уравнений, располлгля их

в столбцах сверху вниз. Во вторую схему (тнбл. 38) выписывают

очередное значения неизвестных, располагая их тикже сверху пика.

При вычислении очередного значения неиявсстиого лопый край

второй схемы прикладывают к правому краю соответствующей графы

цервой схемы, после чего суммируют на арифмометре произведения

соответствующих множителей и свободный член итерационного урав-

нения. По мере заполнения граф второй схемы ее левые графы от-

резают. Приближения продолжаются до тех нор, пока очередные

знлчонпя пензвестных не будут повторяться.

В табл. 37 показано решение системы урпвненнй, которая три-

жды решепа рапсе другими методами. Значение \ри~\ вычислено

по формуле

[рвЦ = - и

Хг

+ Л

,т

+ +

[РШ

Систем

ц у

равняй

п Л

3/Ют

+0,39т

-0.1>8тз-0^ +3.36=0; +6.21;

+0,39т

+ 2,53т

! 0.20x3—0,17т,1+З

Ч4 =

=+63;

-0,28т, +0.2от

+1.08тз -ГО,20Т

—2,02 =

= _ ] ,33;

—ОЛ*,—0,17т, +0,2Ят

+ 1,00X4+2.99=0; 2, = + 1/.5;

[р1/)

= 35.68.

Неизвестные, полученные способом простой итерации, оказались

точнее, чем их значения, полученные но подпой схеме на логариф-

мической линейке.

Отметим важное преимущество способа итерации в том. что

ошибки в процессе приближений лишь увеличивают число приближе-

ний. не отражаясь на конечных результатах. Однако этот способ вы-

годен лишь для хорошо обусловленных систем. При плохой обус-

ловленности число приближений велико, и снособ становится нецеле-

сообразным.

Сделаем еще два замечания по поводу применения способа простой

итерации.

1. При большом чпеле уравнений в схеме I их следует распола-

гать так, чтобы левее оказались большие по абсолютной величине

свободные члены Ьщ. Так, в пашей схеме следовало бы располо-

жить уравнения в такой последовательности: 3-е, 4-е, 2-е, 1-е. Прп

малом числе уравпеппй порядок расположения практического зна-

чения не имеет.

2. Неизвестные нужпо подставлять для контроля во все урав-

нения. Мы этого не делали, так как значепия иензвестиых опреде-

лены ранее.

16 я «кпз и'.о 241

Глава VII

СПОСОБЫ ВЫЧИСЛЕНИЯ ВЕСОВ ФУНКЦИЙ.

ПРИМЕРЫ УРАВНИВАНИЯ С ОЦЕНКОЙ ТОЧНОСТИ

§ 66. ВЫЧИСЛЕНИЕ ВЕСОВ ФУНКЦИЙ

ПРИ УРАВНИВАНИИ ПАРАМЕТРИЧЕСКИМ СПОСОБОМ

Как указано выше, для оценки точности любой вели чипы необ-

ходимо представить ее в виде функции результатов измерений х

после чего можно применить известную формулу теорпи ошибок

1 Г/ЭД» V 1 "1

ТУ

Величина, вес которой требуется найти, может быть по условиям

задачи выражена явно либо через уравнепные значения необходимых

неизвестных I. либо через уравненные значения х\ измеренных вели-

чин. Обозначим оцениваемую величину через Г.

В первом случае это будет

/*).

во втором

*;)•

Но так как все измеренные величины выражаются через необхо-

димые неизвестные в впдо равенств

х', = и(к 1к)

(»

").

то второй случай легко "сводится к первому. Поэтому рассмотрим

только первый случай.

Итак, имеем

Р=ГЦ 1и)

и требуется найти вес величины К. Величины I — не результаты из-

мерении. Поэтому рассуждаем так: ' = т п величину Рможно

рассматривать как функцию неизвестных т. т. с. неизвестных си-

стемы пормальпых уравнений. Если эти неизвестные выразим через

результаты измерений, то задача будет решена: величина Р будет

представлена в виде функции результатов измерений.

Для этого поступим следующим образом. Вп;;чале выразим не-

известные т в виде линейных функций свободных членов нормальных

уравнений. Так как эти свободные члены являются суммами \ра

1\*

[раЛ]. . . то пе составит труда выразить неизвестные в виде

лшн-Гяшх функций I, т. е. свободных членов уравнении поправок.

Т.'.ким образом, задача будет решепа, если учесть, чго вес величины

= /| • • ч

1) — х

{

=х1 — х

равен, очевидно, весу резуль-

тат измерения, т. с. что величины 1

{

при оценке точности играют

роль результатов измерений.

252