Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений

Подождите немного. Документ загружается.

и лд Рк с м у ос та л ьиы х коп ф ф ици с пт о в та к и е

н; с.

к 51 к и 11

Р » с о о т в с т с г в у к» щ и х и о и з в е с т -

X в V Р а В 11 011 И я X того ж О II О М С р а Т! О р В О II а -

п а Л ь I! о И с II С Т С м 1,1. В I» р X II II

II И Д е К С Ы, В С

1С

О б -

к а х. показывают число и с к л ю ч с и и ы х неиз-

вестных до пол у ч е н и я д а н п о и г и с т с м ы.

Теперь легко паппсать любую преобразованную систему уравне-

нии. Так, например, после исключения пяти неизвестных из системы

восьми уравнений будет получено

Л'^-7+-

О,

6-Г-»

'*88

—О.

1>ез затруднений можно написать выражение для последнего не-

известного

И общем случае

дЧ?) '

(т-1)

тт

гдр т — число неизвестных.

Не составит труда написать остальные элимниацнониые уравне-

ния, например,

,у(3) д(3) у(3) дг<3) ;(3)

в * 47

48 _ _ 4

\'<3) \(3) „(з)

ДГ

(3)

41 II 4

44 "44

В общем случае

у(Г-1) \г(|-1) у(|'-1)

г (1-1)

_ -Ч('+1)

I (Г4-2)

' »тп ^ _ I

у«-1) ,-(1-1)

-«>2— •

• • Д-0-1) "

у(|-1) '

ИЛИ

1(1+1)

' ' ' (VI. Ь)

Обозначения коэффициентов и свободных членов преобразован-

ных уравнений раскрываются по следующему правилу.

Коэффициент (свободный член) преобразованной системы равеп

коэффициенту (свободному члену) предыдущей преобразованной си-

стемы с теми же нижнимп индексами минус дробь, в знаменателе

которой стоит первый квадратичный коэффициент предыдущей си-

стемы, а в числителе—произведение двух коэффициентов, у которых

первые индексы такие же, как в зиаменагеле, вторые

—

повторяют

223

индексы уменьшаемого. Некоторые особенности раскрытия обо-

значения свободного члена покажем па примерах

д;(4),у<4)

д-(5>_,у<»)_. "

•

-в

—

Л<!>

5 а

д.-(З) у<0)_

48 ~

.у

(

Л>-л!

" .

у(з)

4 4

у(3)^у(2)_

11 44 ,(2)

• » ао

и т. д.

Свободные члены раскрываются так:

/Л

>=/Л

>—

•"а

'зз

у<1>

оп

В общем случае

у(р-1) у(?>-1)

у(р)

_ у(Р-1)_ *

Р1

РР

у(р-1)/(Р-1>

' Р» "Р

РР

(VI. 18)

причем всегда / ^ I > р.

Раскрывая по указанным правилам коэффициенты и свободный

член любого уравнения эквивалептпой системы, убеждаемся, что

для этого требуется только первоначальная система уравнений и

предыдущие уравнения эквивалентной системы, т. е. из преобразо-

ванных систем нужпы только первые уравнения. На этом и основан

алгоритм Гаусса.

Покажем теперь, что коэффициенты, расположенные на главной

диагонали любой преобразованной системы, всегда положительны,

так как представляют собой сумму квадратов.

Рассмотрим систему исходных уравпеннй

• + =

= 1,.... и). (VI. 19)

Под «исходной» системой будем понимать редуцированные к рав-

цоточному'впду параметрические уравнения поправок или коррелат-

ные уравнения поправок. Во втором случае щ — 0.

ИСКЛЮЧИМ из уравнения (VI. 19) при помощи первого элнмнпа-

цпопного уравнения неизвестное г

. Тогда получим

41^-г- •

•

+ <&>

2т

+и>}

= (у

1.20)

Так как правые части уравнений (VI.20) остаются без изменении,

то пз этих уравнений, исходя из условпя |рV-] — тт, можно полу-

чить систему нормальных уравнений

и т. д.

224

раскроем сумму |в2

«2

Так как

'2 7Г

»•

11 Л

Далее имеем

К'ЧЧ -

[

г1—21я,а

] -

[«,*,] .

Учитывая обозначения коэффициентов нормальных уравнений,

последнее равенство переписываем так:

(1)

(1Л_ у о

У>3

4- у -

Л|;Л

-- у ^иА'м

12 2 3 "'22 "

ЛГи

+Л„

д,

ИЛИ

а согласно формулам (VI .18)

т. е. коуффициеит Л1>У — сумма квадратов, что и требовалось дока-

зать.

Нетрудно убедиться, что

И т. п.

Исключив аналогично при помощи второго элпмнпациошюго урав-

нения из системы (VI.20) неизвестное получим

п т. д.

Таким образом, установлено, что преобразованные системы нор-

мальных уравнений сохрапяют все свойства первоначальной си-

стемы, а именно: по главной дпагопади стоят квадратичные коэффи-

циенты, остальные коэффициенты располагаются .симметрично от-

носительно квадратичной диагонали. Это обстоятельство — большое

достоинство метода последовательного исключеппя неизвестных для

решения системы нормальных уравпешш.

15 Заказ 1140 225

2. Обусловленность системы

нормальных уравнений

Пажненший показатель обусловленности системы лшкч'шых ур

)1и

нений — определитель системы О.

Определитель системы нормальных уравнении легко получить

из системы эквивалентных уравнении. Матрица коэффициентов этоц

системы треугольная. Из теории матриц известно, что определитель

треугольной матрицы равен произведению ее диагональных элемен-

тов. Таким образом,

и—Лц-л.», --»

•• .

''»„,„, • 1.Л)

Отсюда видно, что зпаченне Г) всегда положительно. Для одно-

типных систем одного н того же порядка и одинаковой размерности

коэффициентов исходных уравнении чем больше О. тем лучше обус-

ловленность системы.

Для полной характеристики обусловленности системы необхо-

димо произвести весьма громоздкие вычисления «собственных чисел»

матрицы коэффициентов н нантн «собственные решения». Практи-

чески это неприемлемо.

Приведем следующие признаки хорошей обусловленности си-

стемы нормальных уравнений:

1. Квадратичные коэффициенты заметно превосходят по абсолют-

ной величине неквадратичные. Идеальным считается случай, когда

все неквадратнчные коэффициенты равны пулю, т. е. когда матрица

коэффициентов диагональная.

2. Неквадратнчные коэффициенты группируются вблизи главной

диагонали, остальные элементы матрицы равны нулю. Такая ма-

трица называется б л н з д и а г и н а л ь и о и.

3. Свободные члепы невелики.

Указанные признаки очевидцы н не нуждаются в доказатель-

ствах: очевидно также, что при прочих равных условиях * обуслов-

ленность ухудшается с увеличением системы.

3. Способы контроля решения

нормальных уравнений

1. Копт р о л ь н о в с п о мо г ат ел ь н ы м и с и зве-

с т н ы м. Введем неизвестные

= ! (/«=! "О- (VI.22)

Тогда =

и,-

-+- 1 {/ = I, . . ., т) п можно написать

-V/,

("1+1)-Л'/о К+ 1Н-. •

•

+ А'/я {и

+ ^ =

'п"1 Л'/

-}-.,.+

Л/т"/»» -г (Л/,

...

4- Л'/ш

/./)

=0.

По

Л'д Л'/

-Ь-. + /,/=

* Обусловленность системы ураппепии характеризует точность ее решения.

При плохо» обусловленности иеизвестние будут отягощены большими ошибками,

зависящими от округлении и процессе вычислений.

поэтому можно написать систему уравнении

' • • .тА'

|т

га

-1-2

-'»0 1

1. (VI. 23)

Л'^п,-}-. •

+ Л

-: )

Получен следующий результат: если повторить реш^ин» уравне-

нии со с во о од I г м ми членами, равными (»' = I иг), то полу-

чим контрольные неизвестны?, отличающиеся от о-лновных на еди-

ницу, согласно равопству (VI.22).

Заметим, что для этого контроля придется повторять преобразо-

вания только в одной, дополнительной. грлф^. и которую нужно

выписать суммы коэффициентов и си<юлдиого члена уравнения,

а также вычислить новые неизвестные.

2. II р о м е ж уточи ы е к о и г р о л и. Трудности решепия

системы уравнений заключаются не только к большом объеме, вы-

числений. по н в том, что почти все последующие действия основы-

ваются на результатах предыдущих, из-за чего допущенная в вычис-

лениях ошибка может сделать неверными все послед ующие резуль-

таты. Поэтому в решении нормальных уравнений особую важность

приобретает контроль промежуточных результатов вычислений.

Первый контроль в начале очередного преобразования — это

контроль элпмипационпого уравнения при помощи равенства

(й

«» ±1 /Ч-, о/\

- ШГ" • • — ЛГ ~ - <

х ,24)

где — сумма коэффициентов п свободного члена 1-го урав-

нения эквивалентной системы.

Заметим, что п графу ^ схемы решения следует выписывать точ-

ное значение левой части равенства (VI.24). Правое, контрольное,

значение не выписывается нигде.

Основным промежуточным контролем служит контроль правил ь-

постп вычисления коэффициентов и свободного члена каждого оче-

редного уравнения эквивалентной системы (контроль «по суммарным

строкам»), осуществляемый равенствами типа

+ . . .-ЬА'Г^Ч^'"

- (VI.25)

где — результат преобразования величии

Для осуществления этого контроля с величинами - выполняют

такие же преобразования, как н в других графах. Заметим, что

в графу выписывают точные значения левой части равенства

(VI.25).'

Докажем справедливость равенства ^\1.2;>).

Принимая во внимание (VI.23). можно написать два равенства

*г(«'-1)„. I \Г</-1> 1. у(|-|). I (1-1) ()

Л/(»'-*>,„

_1_

Л ('

-1

и• 4- ! V

>м

- — *•(*-!)

Вычитая нз верхнего равенства нижнее н имея в виду равенство

(VI.22). получаем

уО-и-уа-г) I 4. = у(

/_1

что и требовалось доказать.

При решении пормальных уравнений в параметрическом способе

уравнивания в схему нынпсывают еще зпачепня |/>Л

! и обо-

значпм их так:

( 1)(

"I. (VI.20)

Г/'/*] = 2*М I

Тогда получим заключительное контрольное

равенство решенпя нормальных уравнении

Ниже показано, что

3. Контроль по I ри-\. Присоединим к системе нормальных

уравнений, образующейся при уравнивании параметрическим спосо-

бом, равенство ("У.бО) с учетом принятых памп общих обозначений для

коэффициентов и свободных членов нормальпьтх уравпеппй

Л'и^-Ь. .

.-ЬЛ'итл

+ ^^О,

•

+ Л'а*т

4- 1,

=0,

где

*№«><*«>

= ДОИ"

Вновь полученная система к -{- 1 уравнений с к + 1 неизвест-

пыми сохраняет все свойства нормальных уравпеппй. Поэтому, ис-

ключив нз этой системы все неизвестные т, получим

'(Н1)(Л

[/"-

(VI.27)

Так как велпчниа Л'$+о(*+1) = IрИ] стоит на главной диа-

гонали и играет в преобразованиях роль квадратичного коэффи-

циента, то зиачепие Л^мхаю = раскрывается так:

пли

= Е^У'Ч (VI.28)

1-1

Выражение (VI.28) в впде правила можно сформулировать так:

вел п^ч и н а 1ру

] равна | и л ю с сумма произ-

ведений чисел, стоящих в схеме решеппя на

228

п ер

" • — н « о н и их от р

с»

к с г р а -

ф о й //.на вышестоящие ч и с л а.

Заметим, чго но этому же правилу вычисляют все квадратичные

коэффициенты эквивалентных уравнений, если вместо графы Ь

пользоваться графой Д

Вычисленное по формуле (VI.28) значение [рь

\ должио в пре-

делах точности вычислений равняться тому значению этой же вели-

чины, которое будет получено в таблице коеффицпеитов.

Почти такой же контроль осуществляется при уравнивании кор-

релатным способом.

Присоединим к системе нормальных уравнений, образующейся

при уравнивании коррелатным способом, ривеиство (^.61)

где

'(ГИ)(Г+1)

=1)

Вновь полученная система также сохраняет свойства нормаль-

ных уравнений. Поэтому, исключив пз нес все неизвестные А\ полу-

чим

п;ш

-(^1=2 (VI.20)

1-1

т. е. величина [ри

\ равна сумме произведений чисел, стоящих

в схеме решения на пересечениях элнмпнацпонных строк с графой

И', на вышестоящие числа. Полученное но этому правилу значение

1р«/-] сравнивается с двумя значениями, полученными затем в гра-

фе «у» таблицы коэффициентов и по формуле (У.61).

4. Контроль п е п з в е с т н ы х. После нахождения всех

неизвестных выполняют следующий контроль по сумме уравнений:

+ (2т-^т)г

+ 1Л1»0. (VI.30)

Однако прн решении больших систем уравнении контроль необ-

ходимо выполнять подстановкой неизвестных в эквивалентные урав-

нения после получепия каждого очередного неизвестного из соот-

ветствующего элиминациопного уравнения либо вычислять кон-

трольные неизвестные и =[г — 1, пользуясь суммами коэффициен-

тов п Ь.

Для окончательного контроля результатов уравнительных вы-

числений проверяют, ликвидированы ли невязки в математических

соотношениях между измеренными величинами, для чего составляют

эти соотношения с уравпенпымн значепнямн измеренных величин.

Если уравнивание выполнялось параметрическим способом, то, кроме

•>")Г!

того, проверяют справедливость [шш-т-т. омришиши^ил «юли.-ррцпью

величины через выбранные при уравнивании необходимые неизве-

стные.

Кроме этих поверок правильности решения уравнений. получен- I

иые результаты уравнивания анализируют п отношении качеств,!

измерении н исходных данных, о чем судя

по величинам поправок

и нх распределению в геодезической сети. Нормально поправки у

не должны превышать но абсолютной величине установленных пре-

дельных значений ошибок намерений, а распределение их по абсо-

лютным величинам должно быть более или менее равномерным. Недо-

пустимо большие поправки V являются признаком существенного

влияния ошибок исходных данных либо систематических ошибок

измерений. Распределение же крупных ошибок преимущественно

вблпзп исходных данных также .может свидетельствовать о суще-

ственном влиянии ошибок исходных данных.

§ 63. ПОЛНАЯ И СОКРАЩЕННАЯ СХЕМЫ РЕШЕНИЯ

НОРМАЛЬНЫХ УРАВНЕНИЙ АЛГОРИТМОМ ГАУССА

1. Полная схема

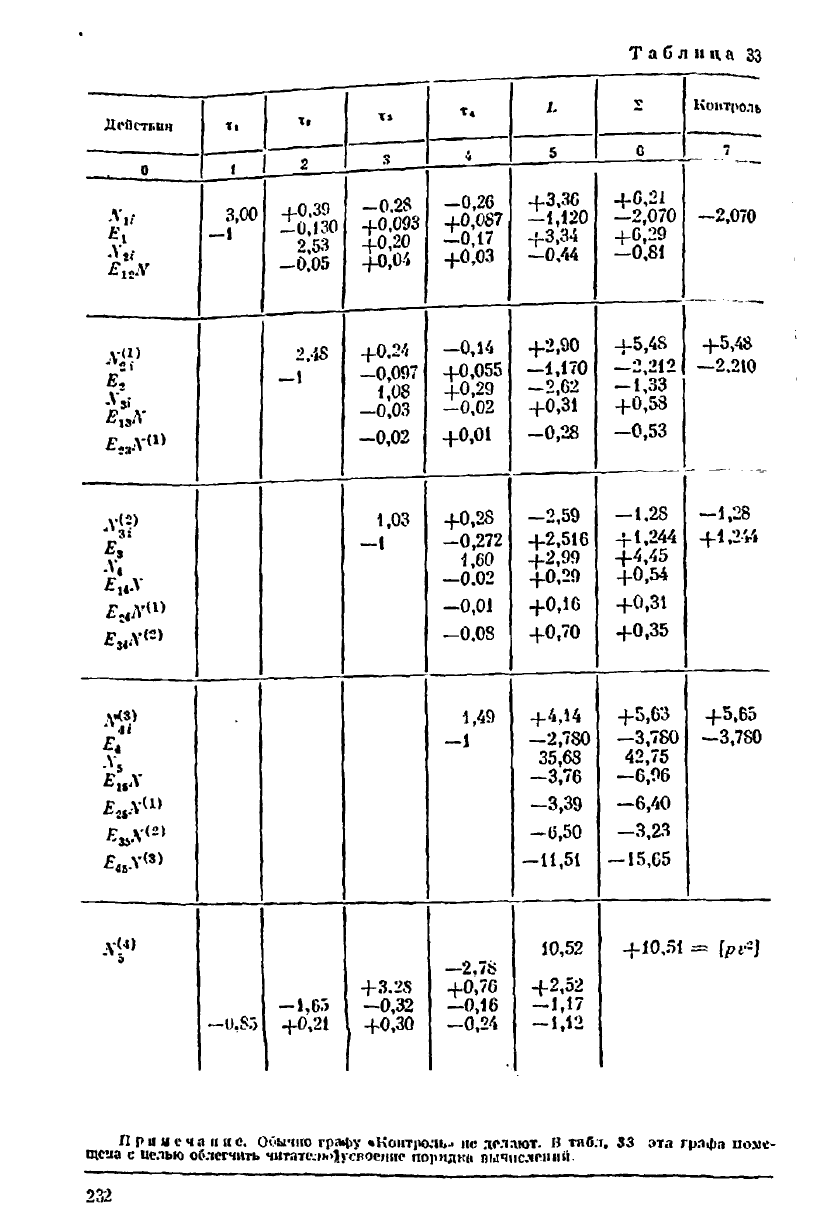
Ниже приведена наиболее полная вычислительная схема алго-

ритма Гаусса, которую обычно называют схемой Гаусса — Дуллтля.

Эту схему можно применять при вычислениях с логарифмической

линейкой. Заметим, что при работе на арифмометре применяют бо-

лее компактную схему.

Для того чтобы показать порядок вычислений в схеме, не при-

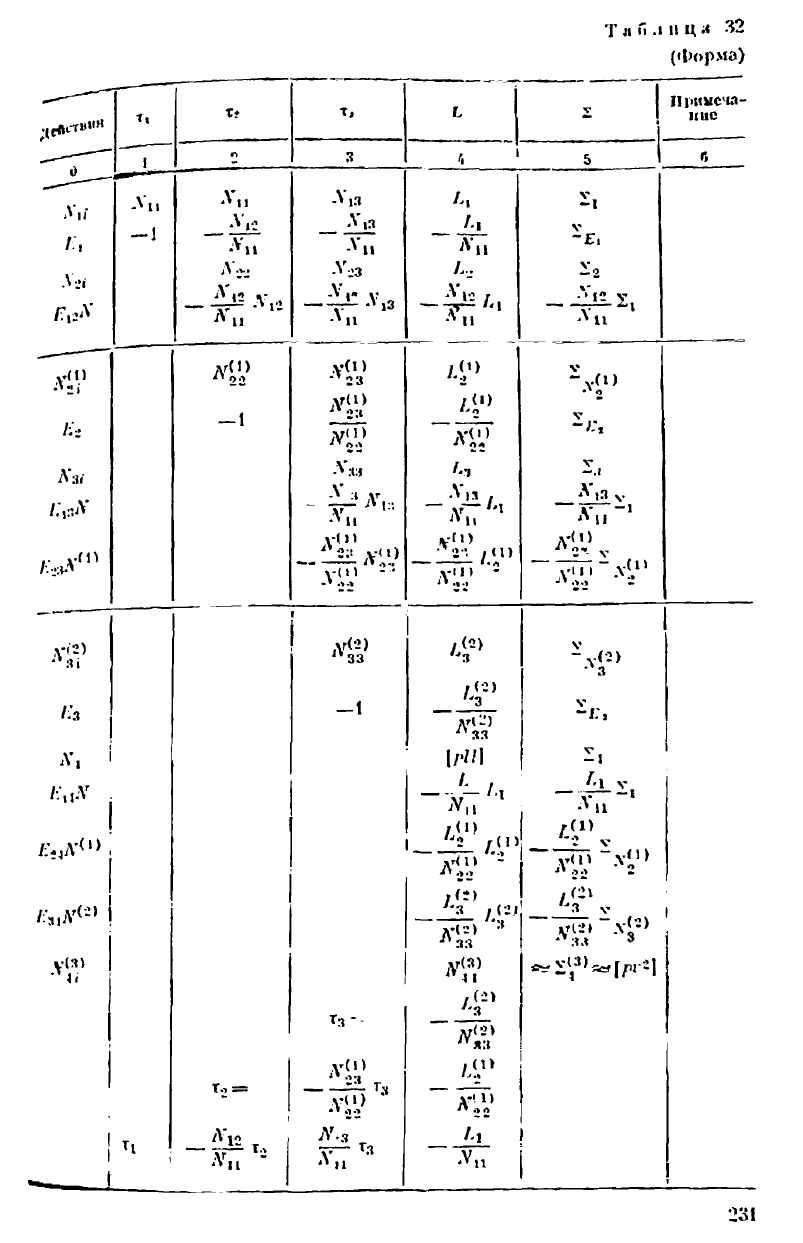
бегая к подробным пояснениям, дадим сначала эту схему в обозна-

чениях. соответствующих формулам алгоритма Гаусса для решения

трех уравнении (табл. 32).

Пояснение к схеме (табл. 32).

1. Все вычисления производят последовательно сверху вниз.

Элнминацноиные строки вычисляют следующим образом. Получив

значение 1 .У

(или

'.Уо^ и т. п.), умножают пто число на осталь-

ные коэффициенты уравнений эквивалентной системы. Так же полу-

чают строки Е|А*, #,

Л\ ДцЛ". /?.>

> и т. и., умножая соответ-

ствующий коэффициент элнминацнонного уравнения на коэффи-

циенты вышестоящего уравнения эквивалентной системы. Заметим,

что числа элимниационной строки имеют всегда знаки, противопо-

ложные знакам вышестоящих чисел (под «вышестоящими» строками

н числами будем понимать строки и числа, стоящие непосредственно

выше над данной строкой или числом).

2. Коэффициенты эквивалентной системы, которые выписывают

иод горизонтальной чертой, получают как сумму чисел даниой гра-

фы. стоящих ниже ближайшей верхней элиминанноипой строки.

3. В графу - выписывают точные значения сумм коэффициентов

и свободных членов соответствующих уравнении. Для основной

системы уравнений в схеме следует применять сокращенную

систему записи, т. е. выписывать только коэффициенты, начиная

230

Т « и .1 и Ц

(форма)

деЛ^»""

Л ,1

Л,.,

/Г,

л"

у'

К-.и

т,

т•

Примет

1-1-1 пне

деЛ^»""

Л ,1

Л,.,

/Г,

л"

у'

К-.и

Гу

5 1 в

деЛ^»""

Л ,1

Л,.,

/Г,

л"

у'

К-.и

Ли

— 1

А'„

А'п

Д -V»

А'п

А 1.4

А'.з

Ам

А',*

/м

/•«

А"„

1-1

А II

-I

-Е,

-2

•* 1С V

деЛ^»""

Л ,1

Л,.,

/Г,

л"

у'

К-.и

««}

— 1

у(1

' 2 3

Л'!,!»

Л'м

- Ь А

,..

у(И

• * а.»

/.<•>

А'1

>••>

X» ,

"А'-

у'О

'«л

у| 1) '

"Л*"

-Г. г

— .1

А" 13 V

л1Л>

Л'.

,„, !

Т1

То =

'» 11

дг<2)

"зз

— 1

ъ-

у(

1 >

г,

У<|)

О'"»

А',Г

/<2>

;<2)

Л'»-)

" 33

/< О

'"г

у<П

л* Л о

.1 /(21

— '«,,

•"зз

" 1 1

ДГ<2>

/Л»

V' 1)

2 2

/•1

Уп

'•1 V

\т< 1 >

л 2

,(21

3 V

у 12» .<•>

2о1

Таблица

Действии

Т«

т»

Контроль

1г

» -

3,00

—1

+0.39

-0,130

2,53

-0.05

-0.28

+0,093

+0,20

+0,04

-0,26

+0,087

-0,17

+0,03

+3,36

-1,120

+3,34

-0,44

+0,21

-2,070

+0,29

-0,81

-2,070

у*

)

Е,

-V*

2.48

—1

+0,24

-0,097

1,08

-0,03

-0,02

-0,14

+0,055

+0,29

-0,02

+0,01

+2,90

—1,170

-2,62

+0,31

-0,28

+5,48

—2,212

-1,33

+0,58

-0,53

+5,48

—2.210

я»

•V*

1,03

-1

+0,28

-0,272

1,60

—0.02

-0,01

-0,08

-2,59

+2,516

+2,99

+0,29

+0,16

+0,70

-1,28

+1,244

+4,45

+0,54

+0,31

+0,35

-1,28

+1,244

\ЧЗ)

*'-!«

Б1Х

Е*

Л<

Е*,У

(3)

1,49

-1

+4,14

—2,780

35,68

-3,76

-3,39

—6,50

-11,51

+5,63

—3,780

42,75

-6,06

—6,40

-3,23

-15,05

+5,65

-3,780

у(4)

—0.8.)

—1,65

+0,21

+3.25

-0,32

+0,30

—2,78

+0,76

-0,16

-0,24

10,52

+2,52

-1,17

-1,12

+10,51

Л р

и с ч

и и с.

ООы-шо графу «Конт]ЮЛЬ->

не

делают.

табл.

33 эта

грпфа поме-

щена

иелью облегчить читатс.и.>1>сяое»|ис порндк« пычисленнй

232