Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений

Подождите немного. Документ загружается.

Н развернутом виде выражение

(VI. 1)

выглядит тан:

).(:'..)._(.': .у

.... Ля» щ/ \ ' \ /

При уравнивании параметрическим способом число уравпепий

/я = к, т. е. равно числу необходимых величин, ь коррелатном спо-

собе от — г, т. с. числу избыточных величии.

Коэффициенты нор.\.альпых уравнений имеют, но сути дела, одну

у же структуру в обоих способах, а именно:

Л*

= |/«7

П/]—в параметрическом способе.

Л*

/«=

[(уоцв/) — в

коррелатном способе.

(Р

1'1] — в

параметрическом способе,

=/--А-у и 1/ = И'/—в коррелатном способе.

Обозначим прямоугольную матрицу коэффициентов параметри-

ческих уравнений поправок или коррелптиых уравнений поправок

через

(

1Ш

Ощ, .... Опт '

где п > от.

В дальнейшем эту матрицу будем называть исходной. Ис-

ходными назовем и

оответствующие уравнения *.

Обозначив транспонированную матрицу через А

, а диагональную

матрицу весов пли обратпых весов —через р или д. можно написать

Л'=А

рА

— для

параметрического способа |

Г-

(

Л"—/! 7.4—для коррелатпого сиосооа ** )

Как установлено, а также следует пз равенств (VI.4). матрица

Л" — квадратная п симметричная относительно главной, квадратич-

ной диагонали, вследствие чего Л*

/ = Л'/

. Поэтому таблицу ко-

эффициентов нормальных уравнений можно ппсать сокращенно сле-

дующим образом:

Ц.

Л 1».

Л'хз. .

Л 1т

Л\,

. .

Л'зз- -

(VI. 5)

Л тт •

* В геодезической литературе элементы разных столбцов исходной матрицы

часто обозначают разными буквами латппского алфавита; прп этом номер столбца

обозначается порядковым номером букпы в алфавите, а номер строки — едпн-

ствепнъв! подстрочным индексом. Например, элементы 4-й строки пишутся а

С, II Т. Д.

** В^транспонпрованной матрице коэффициентов условных уравнений по-

правок в строках будут располагаться коэффициенты коррелатпых уравпенпй

поправок.

т. е. н каждой строке писать коэффициенты, начиная с киидрнтичиогг)

Коэффициенты нормального уравнения с порядковым номером ?

Ч1г

таются так: ;-н столбец сверху вниз до квадратичного коэффициента

п далее вправо по строке, например Л',

. . . Л

,„.

1. Контроль вычислений коэффициентов

нормальных уравнений

Контроль вычислений коэффициентов уравнений осуществляют

так.

Для каждого параметрического уравнения поправок вычисляют

сумму

• -те,-* !•-/,-=*,•

").

после чего иользуются следующими очевидными контрольными ра-

венствами *:

|/Й,Д

1 -, {(>а.О

]

. -г [/^2^1 -г

I/ = [/'

Г/

*1+[№0*1+... -г -г

В коррелатном способе

— (

и),

п контрольные равенства имеют вид

[<7в

в,14-[7<»1Я

]

. . +

[<1<1

— [ча^]

Для контроля в обоих способах в таблицах коэффициентов урав-

нений поправок, при помощи которой вычисляют коэффициенты

нормальных уравнении, дается графа «5».

* Напоминаем, что все коэффициенты уравнении поправок обозначают бук-

вой а; они имеют два нпдекса:

первый (текущий) индекс

обозначает номер строки.

в которой расположен коэффициент (помер измеренной величины); второй — но-

мер столбца в таблице коэффициентов. В сокращенной записи сумм произведе-

ний коэффициентов текущий индекс I опускается. Наиримор, третий член во

«тором из равенств (VI.В) в развернутой записи будет

/>/0^(7,3=- />

Л,з-'

/»2

2С

гЗ

+ • •

•

-г /Л»я„

п„з.

2. Приведение уравнений

к равноточному виду

При равноточных измерениях коэффициенты и свободные члены

нормальных уравнении имеют вид |л,а,1. 1л,а

1. .. Iя,/), т. е.

представляют собой суммы произведений двух множителей Прак-

тически весьма важно, что на вычислительных машинах такие суммы

произведен

и й

можно получать без промежуточных записей отдельных

произведений. Однако суммы произведений вида [ре^я»), 1р«гя

|рЛгЛ и т. п. указанным путем получать труднее, что услож-

няет вычисления. В связи с этим и приводят уравнения к рав-

ноточному виду («к весу единица»). Это преобразование заключается

в том, что все коэффициенты и свободные члены параметрических

уравнений поправок умножают на где » — индекс соответству-

ющего измерения.

После умножения на р

{

редуцированные уравнения можно рас-

сматривать как уравнения для ривноточных измерений. Действи-

тельно, обозначив

и Ур* "п- = )

Рг = ^,

получим

= К,

г1«[рв1в

1 =

чго п требовалось доказать.

Для приведения к равноточному виду коррелатиых уравнений

поправок коэффициенты этпх уравнений умиожают на

При редуцировании уравнений к равноточному виду таблицу ко-

эффициентов дополняют вправо графами . . .. п'

. . . V. $'.

В нижней части этих дополнительных граф выписывают значения

к«;ь \

\<\ кч«т. д.

Если коэффициенты уравнений равны ио абсолютной величине

единице, то редуцировать их к равноточному виду нецелесообразно.

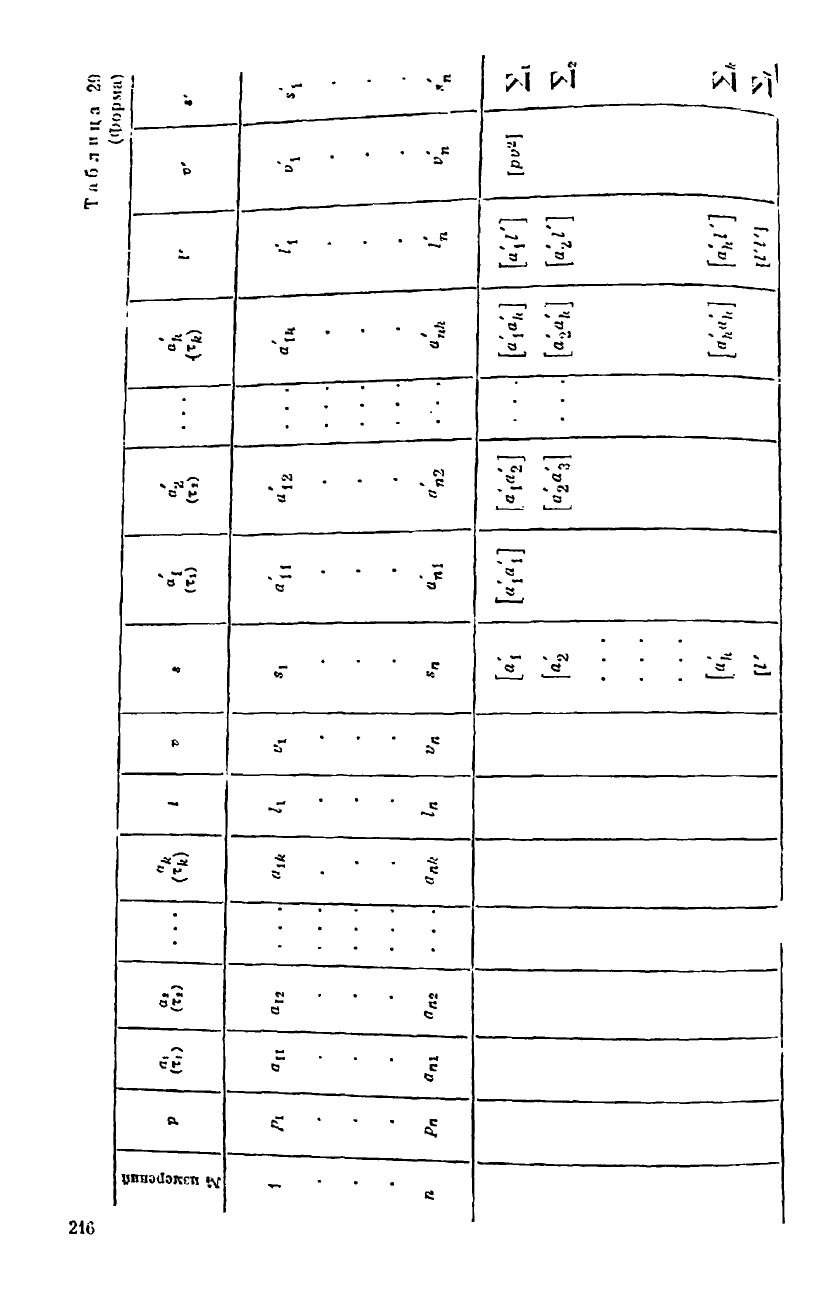
Приведем формы таблиц коэффициентов для двух основных спо-

собов уравипвалня (табл. 29 и 30) в наиболее общем виде. Назначе-

ние граф Р в табл. 30 объяснено в главе VII.

Пояснения к т а б л. 29 (параметрический способ).

1. В графу 5' выписывают точные суммы редуцированных коэф-

фициентов и свободных членов уравнений поправок, которые кон-

тролируют равенствами = л,*! 4- -{-... + а)* + 1\ \

Р»

•

2. В нижней части таблицы в ту же графу х' также выписывают

точные значоппя 2 сумм коэффициентов и свободных членов нор-

мальных уравнений, контролируя этп суммы равенствами

и г. л.

3. Вычисление поправок V контролируют следующим образом:

получают I'} — «0*4 -г ... -г 4- I' и затем проверяют равен-

ство 1)\ 1\

]/"/>»'

"•0

. - • • • ч*

у \ >1 ; • ; Н | ^ \

. и - я • * - '

>- Л • • -Ч

с г . а

, - • - - . С

^ V

- - V е» V ^

ь.

- • • . ё

в Ъ

Г~»Г ч I»' " " * '—

= с . . .

- - • « «V

а <г ^

•

* « • • С

с а

« ГЧ

Су • • •

. с

ч «

.1.-1 . . . • 1.

^ ^ а _ с

ь.'

•Г - - •

ь.

а* • • • а

^ . . . в

с в

•

• • •

•

с •*

в • • • «

сГ ••• .5

—

^ . . . =

• • ' ^

утюс1

-.1К| Ц

- ' ' к

Нетрудно убедиться. что |рг

1 - (г'г'

I-

Контролен служит щ*,

числение [ро'

\ в схеме решения нормальных уравнении в графе

свободных членов.

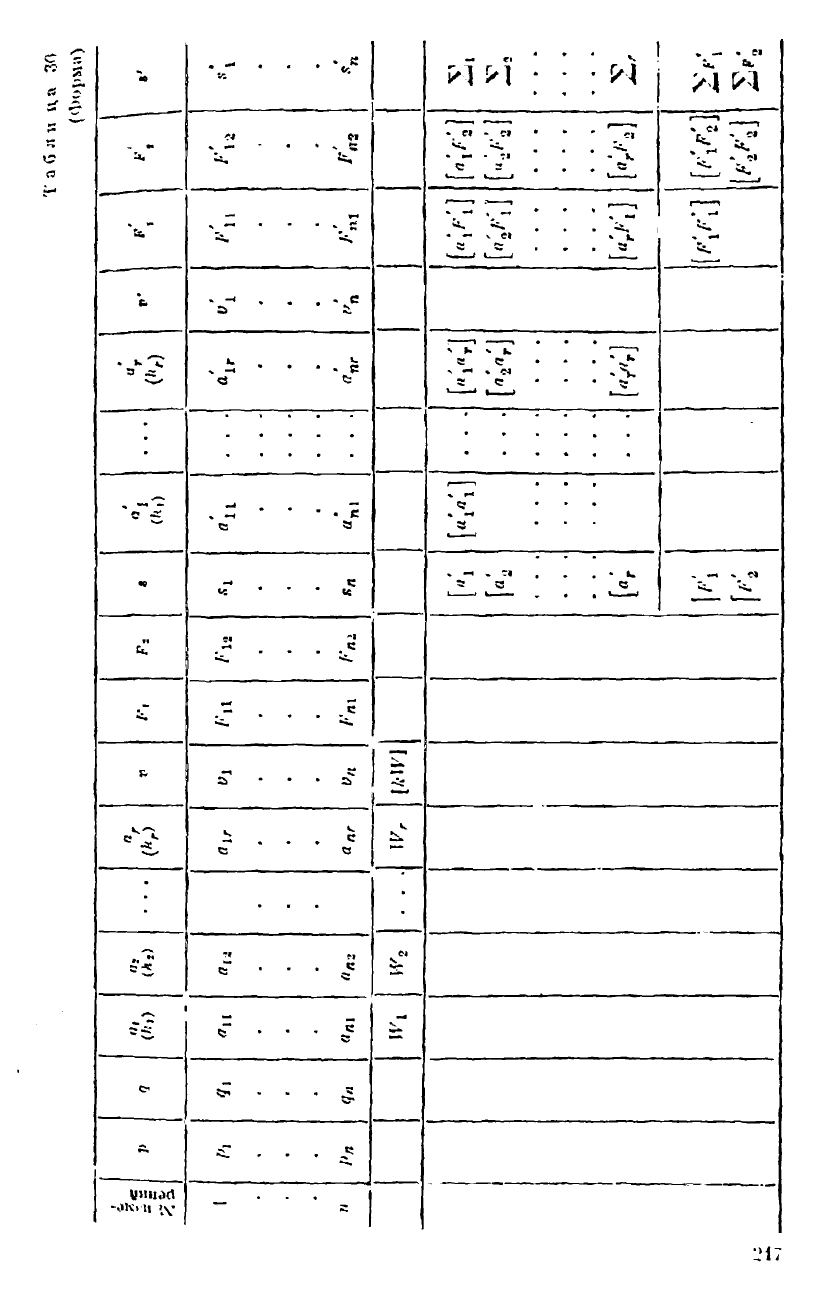
П о я с и е н и я к т а б л. 30 (коррелаты

способ)

1. И сумму .Ч,- входят величины /*, , и И сумму А,- — всмц.

чины

» П* ('V -^г)'

где /•' — некоторая функция переменных .г, х

2. \рг~\ |г'гЧ. Кроме того. -

—

|ЛИ']. Третий раз

1/>г

| получают в схеме решения нормальных уравнений коррелат,

в графе

<>И

». по правилу, которое будет получено ниже.

И остальном к габл. 30 относятся все за .меча пня. данные в по-

яснениях к табл. 2У.

Сделаем еще одно важное замечание, касающееся заполнения

как одной, так н другой таблицы.

Неизвестные в параметрических уравнениях поправок п условные

уравнения поправок необходимо нумеровать так, чтобы левые гра-

фы «а» таблиц были заполнены меньше, чем правые, т. е. в этих

графах должно быть больше нулевых коэффициентов. При прочих

равных условиях коэффициенты, равные ±1, также нужно распола-

гать возможно левее.

Для коэффициентов исходных уравнении, как правило, оказы-

вается достаточно сохранять три значащие цифры, а для свободных

членов — две-три. Для коэффициентов и свободных членов нормаль-

ных уравнений всегда достаточно иметь три значащие цифры.

Соблюдение всех рекомендации, которые даются в пояснениях

к таблицам коэффициентов, существенно облегчает уравнительные

вычисления.

Напоминаем, что прн равноточных измерениях, а также в случае,

если все коэффициенты во абсолютной величине равны единице,

правые части таблиц (отделенные ДВОЙНОЙ чертой) не нужны.

§ 62. РЕШЕНИЕ НОРМАЛЬНЫХ УРАВНЕНИЙ

1. Алгоритм Гаусса

Решение системы нормальных уравнений, как правило. — наи-

более трудоемкая часть уравнительных вычислении, поэтому заслу-

живает особого внимания. Осуществить это решение можно разными

способами.

К. Гаусс подробно разработал способ решения, основанный на

методе последовательного исключения неизвестных, и ввел очень

удобную систему обозначений, облегчающую решение. Этот способ,

который называют а л горит ..I о м Гаусса, подробно рассмо-

трим. Огмпим. что при наиболее эффективных способах решения

больших систем нормальных уравнений в тон или иной степени ис-

пользуют алгоритм Гаусса.

218

Сиособ определителен, к»к показынаст практика, имеет- несо-

мненные преимущества лишь при решении днух уравнений. При

решения больших систем способ определителей едва ли сможет кон-

курировать с алгоритмом Гаусса. Го же можно сказать н о многих

других слое оба

лишенной алгебры дли решения систем нормальных

уравнении.

При наличии вычислительной машины тина арифмометра коли-

чество записей при решении системы нормальных уравнении алгорит-

мом Гаусса .можно значительно сократить.

Еще более эффективен способ крлиовяпоп. в наибольшей степени

использующий возможности вычислительных машин, особенно элек-

тронно-цифровых.

При решении очень больших систем, состоящих из многих десят-

ков и даже сотен уравнении, применяют метод приближении: при

решении большого числа уравнении, распадающихся на частично

независимые системы, может быть применен способ Праинс-Праие-

внча. Вопросы решения больших систем нормальных уравнении рас

смотрены в главе X.

Рассмотрим алгоритм Гаусса.

Каи указало, в основе алгоритма Гаусса лежит метод последова-

тельною исключения неизвестных. Гаусс ввел удобную систему обо-

значении. облегчающую теоретическое рассмотрение вопросов и за-

поминание порядка действии; однообразие последовательных дейст-

вии и надежный контроль правильности промежуточных результа-

тов вычислений являются большим достоинством этого способа.

Рассмотрим алгоритм Гаусса на примере решения систем четырех

нормальных уравнении

Напоминаем, что система нормальных уравнении обладает сим-

метричностью неквадратнчных коэффициентов относительно главной,

к в а д р а т и ч н о й. диагонали, т. с. —

Выразим первое неизвестное через другие из первого уравнения

Равенство (VI.8) называют э л н м н и а ц и о и и м м у р а в -

и е и н е м (слово «элнминациониып» происходит от латинского

слова еГпшпо, означающего «выносить за порог», исключать).

Подставим значение г, из (VI.8) во второе, третье и четвертое

уравнения системы (VI.7), после чего, учитывая симметричность ко-

эффициентов, получим

(М.7)

219

Преобразованная после нсключепня первого пепзвестпого система

уравнений сохраняет свойство симметричности пеквадратпчиых ко-

эффициентов (что является следствием симметричности коэффициен-

тов первоначальной системы).

Введем обозначения

_ .,(1)

1г

—

•

« 1М1

Л'гз-

-Уп

ЛУчАУч

Лзз

~~л7Г~ ^

<1>

: У

23 •

_ -У^Уц _

(1)

Л 31 л/ — -»

Ло|

I,-

» - .у(П

УцА г(1)

.V — »

'31

Ьз-

Л'44-

ц-

•Уц

'II

'и

'и „(О

~ "44

ЛИ

Л',4^1

Л'.

(У1.9)

;

Зиак обозначает, что исключено первое неизвестное.

Теперь преобразованная система примет вид

+ Л'^г.ч + Л'^

4 -±-4

+ 44=3 + Л'< \>=

-Ь

^ « О

(VI. 10)

Исключив из згой системы уравнений второе неизвестное, полу-

чим второе элпминацпонпое уравнение

уШ Д'(1)

•• /у о

II о.»

,у(1)

,у (X)

(VI.

И)

и вторую преобразованную систему уравнений

) И'--^Н1

" —яг)=

л'

(

Л> ) л-'» /-+Г'

220

Последняя система уравнений также сохраняет симметричность

коэффициентов.

Далее введем обозначения

зз~ ..(,) ^зз

и" =

22 22

у(1)у<>) ЛГ<»>/(1)

(г)

_ • ,.

(8) (|)

гз

-2

(2)

3» дг(1)

—

31' з » '

22 •'*22

Л.

(1)^(1)

дг(1) *

после чего вторая преобразованная система уравнении примет вид

л^+Л-^+^-О Г

Теперь получим третье элимпнацпониое уравнение

(\ 1.12)

у(2> /<

*31 3

=3 =

""Т?<аГ

г4

~"лТгГ (VI. 13)

зз зз

п третью преобразованную систему

/ Л'

(

-К\

:(2

> \ I .у(2)

(2)

и<»>-

84 3<

1 /Я-

34 3

ио

/ * V

/ '

или применительно к обозначениям Гаусса *

ЛГ<

;

+1,<

>=ГО, (VI. М)

откуда

/(3)

Вычислив 2.

, обратимся к элиминацнонному уравнению (VI. 13),

из которого получим 2

. Далее, подставляя 2

и г

в уравнение

1.11),

находим г„ и, наконец, при помощи уравнения (У1.8) получим

Нетрудно видеть, чго для отыскания неизвестных необходимо

иметь только элпминациоиные уравнения (\

1.8), (VI.11), (VI.13)

и (VI.15), которые получаются из первых уравпешш систем (VI.?),

(VI.10). (У1.12) и (VI .1-4).

Решение системы нормальных уравнений рассматриваемым спо-

собом и заключается в получении первых уравпешш преобразо-

ванных систем, а из них — элнмлнацпонных уравнений. Остальпые

* Мы изменили внешний вид обозначешш, впеденвых^Гауссом. У Гаусса:

л'Й> =

• 1 ]

ИЛН

Л'м -

I «ьь •»1; =* 1Р

ь1

•

пл

I •

Ы^м = •

пли Л'5|> =

[(}сс •

2]; влн

= \ \\'

2] н т. д.

211

уравнения преобразованных систем оказываю гея ненужными. Чтобы

в атом убедиться, выпишем коэффициенты и свободные члены

первоначальной спстемы нормальных уравнений, а в нижней части

табл. 3] — коэффициенты н свободные члены первых уравпеплй

первоначальной н преобразованных систем н элнмпнацнонных урав-

нении. применяя для последних обозначения Е{ (/

г1)

, </»-«>* Ё,

и т. д. (для /-го уравнения).

Теперь нетрудно видеть, что любой элемент ппжнон частп табл. 3!

можно получить, используя данные верхней части табл. 31 и учиты-

вая структуру равенств (VI.8), (VI.! 1), (VI.

13)

п (VI. 15).

Таблица 31

Л|,

Л', г

Уж,

Л*.»

л*«

•V.*

Л'»4

Л 4

Г.,

1-4

•V»

-V,!

1*1

Е |

Ей

уО>

" 22

уП)

' 23

\-<11

'4°

Е-х Ец

"ЗЗ

\*(2>

434)

Ем

у'{31

/(2)

Заметим, что табл. 31, по существу, н лежит в основе вычисли-

тельной схемы решеппя нормальных уравнений алгоритмом Гаусса.

Первые уравнения всех систем в совокупности образуют э к в и -

в а л е н т н у ю систему, имеющую вид

+ Л 12-2"Т Л 13-3"Г Л*! 151 -р Л

— О

Ч,4-Л

,(1

Ч + А"

<|,

-1

.-./СО —О

81 .9"® г 21"'

2 —

+ -О

(VI. 16)

Теперь становится ясна принятая система обозначении. 13 каж-

д о й п р е о б р а з о в а п и о й системе коэффициент

при первом неизвестном в первом у р а в н е-

н н и и м е е т т е ж е н и ж и и е н и д о к с ы, что и у ква-

дратичного к о э ф ф н ц и и и т а и р и т о м ж о н о и з -

в е с т н о м в порви» а ч а л ь н о и с и с т е м с. Н и ж и н с

222