Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений

Подождите немного. Документ загружается.

—

'•родолжоппг. 13

Сопротивление

«,. Ом

—*0

«Г

_о -

Рсшсппс

121

115

116

4-21

4-15

4-Ю

—6.9

-0.9

-1.9

==6.2100

-У-= 0.00141

х»=621141

—304 •

10-"

(г-6.211

304)

4-650X

X 10-4

1.149^

X 10-»

-г 117.7

—119.1

0.230Х

X10*

==6.2100

-У-= 0.00141

х»=621141

—304 •

10-"

(г-6.211

304)

4-650X

X 10-4

1.149^

X 10-»

(

о1=

=-1.4х

X 10'

0.230Х

X10*

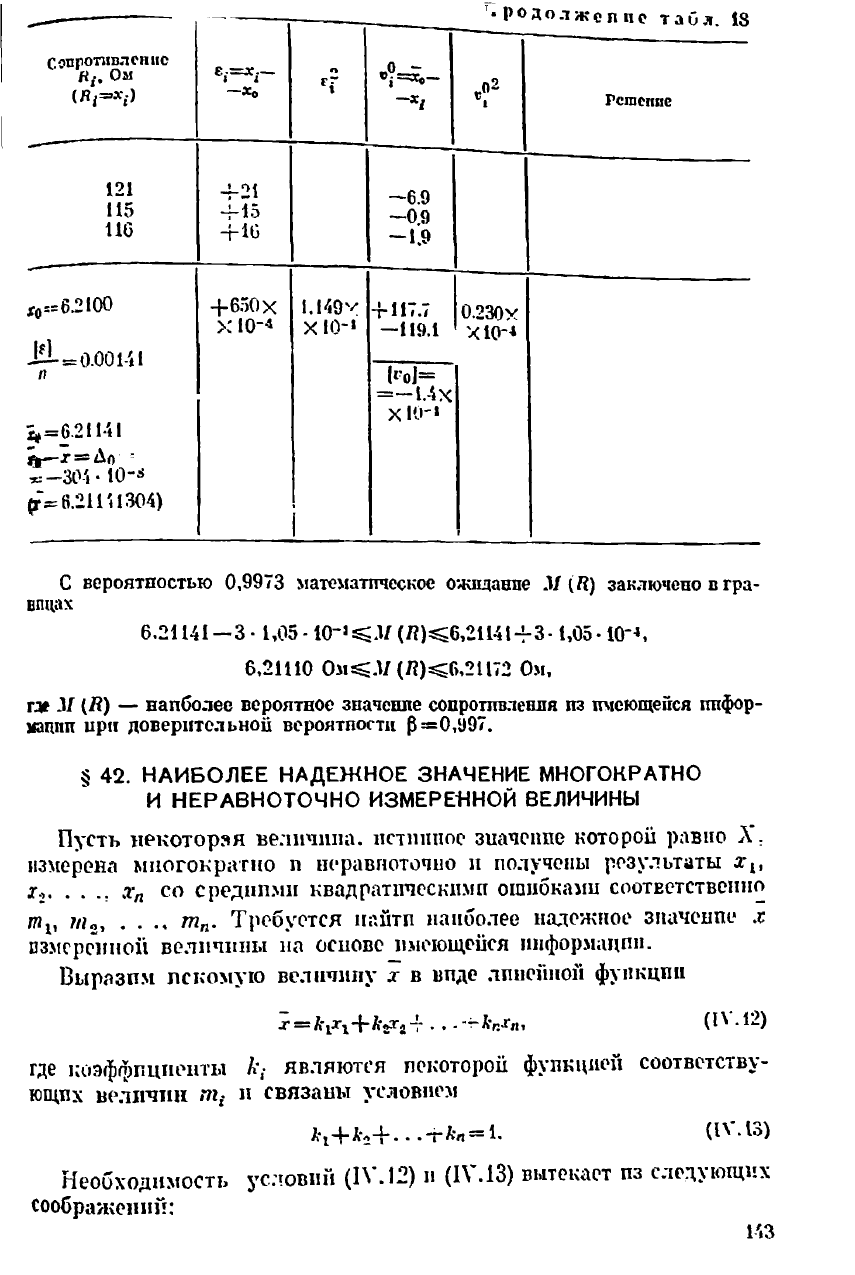
С вероятностью 0,9973 математическое ожидание М (И) заключено в гра-

ницах

6.21141-3

•

1,05

10-^Л/ (Л)^6,211414-3-1,05-10"*,

6,21110 Ом^Л/(Л)^6,21172 Ом,

где М (Л) — наиболее вероятное значение сопротивления из имеющейся инфор-

мации ирн доверительной вероятности р=0,997.

§ 42. НАИБОЛЕЕ НАДЕЖНОЕ ЗНАЧЕНИЕ МНОГОКРАТНО

И НЕРАВНОТОЧНО ИЗМЕРЕННОЙ ВЕЛИЧИНЫ

Пусть некоторая величина, истинное зиачеиие которой равно А",

измерена многократно и неравноточно и получены результаты аг^

. . .. х

со средними квадратпческимп ошибками соответственно

, . . .. т

. Требуется найтп наиболее надежное зиаченпе .с

измеренной величины на основе имеющейся информации.

Выразим искомую величину х в виде линейной функции

х = А-

-ЬАчг

-;- . .. ~Аух„,

(IV. 12)

где коэффициенты к

{

являются некоторой функцией соответству-

ющих величии т

{

и связаны условием

= (IV. 13)

Необходимость условии (IV.

12)

(IV. 13)

вытекает пз следующих

соображении:

151)

Р.1

вноточпые измерения должны рассматриваться как частный

случай неравноточных. поэтому для случая равноточных измерений

будем иметь

Формулу (IV.

13)

можно теперь представить так:

т. е. рапее получепиая формула (IV. 1) для равноточных измерений

есть частный случай формул (1У.12) п (IV. 13), когда к

= А-«—...

2. ЕСЛИ все результаты измерений случайно окажутся равными

между собой, т. е. х

= х* = ... = х

= х, то, очевидно, буд^м

иметь

это еще раз подтверждает необходимость соблюдения условия (IV. 13).

Коэффициенты А-,, к», . . к

найдем при условпп, чтобы ве-

личина х была получена с наибольшей точностью, т. е. с возможно

меньшей средней квадратпческой ошибкой.

Согласно формулам (1У.12) п (111.43) и принимая результаты х

{

независимыми, получаем

Таким образом, задача свелась к задаче па условный экстремум:

требуется найти минимум функции

= т

=... =т

—

т, откуда А-

=А-

=. . . = к

=к,

п'формула

(IV. 12)

примет вид

х=к КЧ-Ха-Ь .

•

+*/.).

а условие

(IV. 13)

будет пк = 1, откуда

х —х.

По формуле (1У.12) для этого случая напишем

но, учитывая равенство (IV. 14),

(IV. 14)

1 2

I »5 5 I •

* о

~А-т+. .. + к~т-.

(IV.

15)

(IV. 16)

у.,д.

чу решим по методу Лаграпжа. Напишем функцию Ла-

рани<»

л — подлежащий определению коэффициент, называемый множи-

мом Лаграпжа. Далее возьмем частпыс производные фуикции

о всем переменным /с,- и приравняем их пулю

ЭФ .

-щ- = 2т?Л,-2л=0 = 2, . .п), (IV.П)

откуда

= ——(1 = 1, 2. . .п). (1\\18>

в. г

Возьмем теперь сумму этих равенств

Но, согласно (IV. 1ь), сумма 1М = 1, поэтому

"Ш

п равенства (IV.18) примут вид

т г

• (IV. 19)

Выразив в линейной функции (IV.12) коэффициенты к

через-

найденные для ипх значеипя, получим

= ;

(IV. 20)-

1-1

т?

Формула (IV.20) решает поставленную задачу. Однако она может

оказаться неудобной для вычислений, если величины то,- будут

сильно отличаться от единицы. Для удобства вычислении выбирают

безразмерный коэффициент и", на который умножают чпелптепь

п знаменатель правой части форму:-,ы (IV.20), после чего она примет

впд

Ж^гО

(-1 *

* = » (1У.21)

V И®

/| о

** т~

По

Величину и

выбирают с таким расчетом, чтобы отпошеиия 111

* ' **

были возможно блпже к единице.

Для удобства вычислении измеренные величины выражают в та-

ких единицах меры, чтобы величины /и,- также были возможно ближе

к единице. Так, например, если средние квадратичеекпе ошибки пз,

моренных расстояний имеют порядок от 5 до 10 см, то расстояния

н пх средние квадратичеекпе ошпбкп удобиее выражать в децимет-

рах.

Величины ~ называют веса м и соответствующих результа-

ту

тов х, и обозначают через т. е.

и-

(1\\22)

тг

С учетом выражения (ГУ.22) формула (1У.21) прпмет вид

- [рг]

X = •

\р)

(IV. 23)

Величину х, полученную по формуле (1У.23), пазывают весо-

вым средним или общей арифметической сре-

диной. Нетрудно видеть, что среднее весовое не изменит своей

величины, еслп все веса будут умпожены на какое-либо постоян-

ное, не равное нулю, число. Отсюда следует, что для получения

наиболее надежного значения неравноточно измеренной величины

достаточно знать соотношения средних квадратических ошибок;

сами же величины т

могут оставаться попзвеетнымл. Поясним это

положение.

Предположим, нам известны отношения

тп

т, " " =

где т

— средпяя квадратическая ошибка некоторого результата а:,.

Величины го, (г = 1, 2 г л) нам неизвестны. Приняв

р = ст

, где с также неизвестно, можно паписать

т; _

1 р- 1

—

2 о .о р!.

т^ с-т!

тог

откуда

Теперь формуле (IV.23) можпо прпдать вид

- _ с- [д-т]

\р) ~ с- (?'-) '

т. е.

(к-1 •

130

(IV. 25)

Таким образом, для вычисления х достаточно знать лишь отноше-

ния средних квадратических ошибок, т. е.

, т

причем квадраты этих отношении будут играть роль весов. Однако

останется неизвестным коэффициент и, необходимый, как убедимся

ниже, для оценки точности.

ряботке ш

В §42

§ 43. ОБЩИЕ. СВЕДЕНИЯ О ВЕСАХ;

ОШИБКА ЕДИНИЦЫ ВЕСА

Веса являются вспомогательными числами при совместной об-

неравноточпых ИЛИ разнородных пзмереппй.

§ 42 сказано, что еслп — средняя квадратическая ошибка

результата измерений, то вес р

этого результата находят по фор-

муле

ц-

А = • (I \\26)

где и- — безразмерный коэффициент.

Изложенное понятие веса для измеренной величппы принято п

для любой функции Р измеренных величин: вес Рр функции Р при

известной ее средней квадратпческой ошибке т

вычисляют по фор-

муле

Рр=-~г- (П\27)

шр

Таким образом, веса результатов измерений и

пх функций являются положительными чис-

лами, обратно пропорциональнымп квадра-

там пх средних квадратических ошибок.

Если = 1. то численно р = т,. На этом осповании велнчпну

и называют «ошибкой е д и и п ц ы веса». Опа равна числен-

ному значению средней квадратпческой ошибки результата, вес ко-

торого численно равен единице и размерность может быть любой.

Согласно (1У.27), наппшом

^=77=г <

1У

и =м

УР} (1У.29>

В соответствии с формулами (1\\2б)—(1У.28) при вычислениях

с весами в практике встречаются два тина задач:

1) установление весов перавноточных или разнородных резуль-

татов с целью совместной обработки этих результатов;

2) отыскание весов функций перавноточных илп разнородных

результатов для получения затем но формуле (1У.28) средней

<п* 1

квадратпческой ошибки т? функции Р. т. о. для оценки точности

ото» функции.

Как видно из формул (IV.20) и (IV.27), для установления весов

но известным средним квадратнческим ошибкам достаточно устано-

вить величину р. Так как все веса в каждой конкретной задаче можно

умножить пли разделить на любое положительное не равное нулю

число, то, очевидно, выбор величппы р при установлении весов

ничем не ограничен ни в отношении ее числового значения, ни в от-

ношении размерности. Поэтому величину р проще всего считать без-

размерной (отвлеченной). Отсюда следует еще. на осповании формул

{IV. 26) и (IV.27). что размерность веса обратна размерности квад-

рата средней квадратпческой ошибки (дисперсии).

Формула (1У.28) является основной при оценке точности функций

измеренных величин. Если коэффициент ц известен, то для подсчета

средней квадратпческой ошибки т? функции этих результатов нужно

определить вес этой функции.

Веса однородных результатов являются относительными числами,

и в тех случаях, когда неизвестны средние квадратические ошибки

этих результатов, их веса можпо устанавливать, используя соотно-

шения средних квадратичеекпх ошибок, исходя, например, пз числа

измерений. В подобпых случаях для получения оценок вычислен-

ных значении функции обычио возникает необходимость определе-

ния ошибки единицы веса р и весов вычисленных значений функции.

Таким образом, задача оцепкп точности функций измеренных вели-

чин подразделяется на две задачи: определение ошибки единицы

веса и определение весов функций.

§ 44. ВЫЧИСЛЕНИЕ ВЕСОВ ФУНКЦИЙ

Задача определения весов функций является одной из основных

задач теории ошибок.

Рассмотрим, как определить вес функции Р — / (.г, у, . ... и)

по известным весам р

, р

, . . .. р

некоррелированных аргументов.

Воспользуемся формулой (III.41) для средней квадратпческой

ошибки гп

функции Р

Разделив обе части последнего равепства на р-, получим

= (ЛИУ Щ*-л. (М-УШу.

V О*/о Ц-

"Г"

\ ду )о .1- ' •

О»

Так как

» '

= (I \".30)

то окончательно напишем

7Г

888

17 + \ 77+- • • + Ы)о•

<•

31>

151)

Величину, обратную весу, называют обратным в е с о м и

обозначают обычно буквой <7.

д™

у1ШЯ К0

РР

ел1|

Рв»«пиых аргументов, в соответствии

с (111.40),

± = + , (<>г \ |

Рр \ их Уо РЛ-

ау )

0 Ру

т ' • • • ^

0и

)

Примеры подсчетов весов функций.

1. Вес суммы перавноточных слагаемых

. т-Хд,

имеющих обратные веса соответственно . , д„. По формуле (1У.32)

вапшпем

+ +

• . + ?п =

1?1.

(IV.33)

Следовательно, обратный вес суммы перавноточных

слагаемых равеи сумме обратных весов слагаемых.

2. Вес и средняя квадратическая ошибка сред-

него весового. Представим формулу (1У.23) в виде

Р1 , Ра , , Рп

~ 1Р1 1Р)

ХЯЛ

' •

И *

Теперь применим формулу (IV.30)

1 Р1 1 . Р1 _1_ , Рц I |р1 1

^ - 1Р]2 •

Р1

+ [рГ- ' р

•

• • + 1РГ- •

Ри

1р]= [р] '

или

/>.=1Р1.

\".З»)

т. е. вес среднего весового равен сумме весов резуль-

татов п з м е р е п и н.

Средпяя квадратическая ошибка М среднего весового, согласно формулам

(1У.28) п (IV.34), будет равна

(I \\35)

I [Р!

О способах получения ошибки единицы веса

сказано в § 46.

3. Веса звеньев системы высотных ходов.

Под системой высотных ходов будем понимать систему ходов геометриче-

ского или тригонометрического нивелирования, в которых высоты передаются

через короткие стороны.

Напишем для звена между узловыми пунктами

/Л)|=-Ах+л

+ ..

где (//. — //

)

- — измеренное зиачепие разности высот концов 1-го звена,

имеющего щ передач высот, к — измеренное значение превышения по одной

передаче.

Считая точность одной передачи высоты по одной стороне'нлп между двумя

рейками одинаковой по всем звеньям п полагая ее вес равным р, легко найдем

вес Р; звена, содержащего л,- передач,

или

Р{

I р > р

Р{ — •

Так как все веса в одной задаче можно умножнть'ваТлгобое положительное

не равное нулю число, то окончательно получим

Р, - (П'.Зб)

Коэффициент с подбирают так, чтобы веса ввеньев Р,- былп близки к еди-

нице.

Для равнинной местности, когда можно считать, что длины сторон или

расстояния между рейками приблизительно равны между собой, можно написать

(IV. 37)

где Ь(

—

длина хода.

4. Вес превышения, полученного тригонометри-

ческим нивелированием.

Решая поставленную задачу, считаем источником ошпбок тригонометриче-

ского нивелирования только ошибку измерения вертикальных углов. Тогда

для установления весов можно учитывать только главный член формулы триго-

нометрического нивелирования

к=5 1да.

Еслп угол а невелик, то можно написать

И <=»

•

а,

где угол а выражен в радпанпон мере.

Сторону 5 будем считать безошибочной. Тогда

Полагая точность измерения углов наклона одинаковой, полупаем

Чпсло с подбирают так. чтобы веса Рн оказались близкими к едпвпце.

5. Веса средних арифметических. В практике геодезиче-

ских работ нередки случаи, когда приходится иметь дело с однородными вели-

чинами каждая из которых получена как среднее арифметическое пз п,-

приемов одинаковой точности, и систематические, влияния не учитываются.

В таких случаях среднюю квадратическую ошибку Л/,- величивы находят

по формуле

{

= -р=г> (IV. 39)

где т — средняя квадратпческая ошибка одного приема.

150

На основании равенства (1У.39) напишем

л,*

Полагая и

= ст

. па ходим

т-

—-

Л/?

ст- и 2

ПЛИ

Л=сп

(IV. 40)

. е. вес среднего арифметического пропорционален числу приемов

при условии, если систематические ошибки измерении отсутствуют *.

Кяк видно, систему весов в некоторых случаях практики можно

устанавливать, не зная средних квадратических ошибок величин,

участвующих в обработке.

При наличии систематических ошибок формула (IV.40) непри-

емлема и веса средних арифметических необходимо устанавливать

пп формуле

Рг (П*.41)

где

М; =

П{ ' А,-

для чего, конечио. необходимо знать характеристики систематических

влиянии т

и А", (см. формулу (1У.5)].

Все полученные формулы для весов функций верны лишь прп

некоррелированных результатах измерений. Еслп же результаты

измерений коррелпрованы, то веса определяют по формуле

11=

где величина Мр должна определяться по формуле (III.40).

§ 46. ИССЛЕДОВАНИЕ РЯДА

НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ

Прп исследовании ряда ошибок перавноточных однородных изме-

рений эти ошибки предварительно нормируют, т. е. получают отно-

шеипя

—1

= сохраняя для /,• знаки 6,-. Ряд нормированных оши-

бок исследуют так же, как ряд ошибок равноточных измерений.

Если средние квадратпческие ошибки иеизвестпы. то нормиро-

вание выполняют по формуле (см. табл. 10)

и,-=6,-1 />,.

* Что быпает весьма редко.

Так как

и/=0

' ]/ "Й'^'^Н*

(1Уу,2

то величины м, - рассматривают в дальнейшем как ошибка

равноточных измерений. Очевидно, что умножение всех нормирован-

ных ошпбок на некоторый постоянный коэффициент и не изменит

характера распределения ошпбок.

§ 46. ВЫЧИСЛЕНИЕ ОШИБКИ ЕДИНИЦЫ ВЕСА

Рассмотрим способы вычисления ошибки единицы веса р, при-

меняемые в геодезической практике.

I. Вычислен пе ц при у станов.тении весов

но известным средним квадратическнм ошиб-

кам измерений /л,-. В этом случае веса устанавливают по

формуле

» **

Рг-

тг т-

в которой коэффициент к назначается, и ошибку единицы веса и

вычисляют по формуле

= (IV. 43)

2. В ы ч и с л е н и е и по известным средним

квадрат и ческим ошибкам и весам однород-

ных результатов. Пусть известны средние квадратпческие

ошибки т

однородных результатов и независимо от средних квад-

ратнческпх ошпбок т

{

были одинаковым образом установлены веса

р1 этих результатов, как, например, прп выводе формул (1У.37)

и (IV.40).

В этом случае для каждого результата вычисляют ошибку еди-

ницы веса

М/

= т

11 (IV.44)

и окончательное значение и находят по формуле

~ , (IV. 45)

где п — число результатов, для которых были установлены т

и р

причем предполагают, что надежность знченпй т

{

примерно оди-

накова.

3. В ы ч и с л е н и е р по и з в е с т и ы м истинным

ошибкам 6/ величин, независимо полученных

измерениями, п весам р

{

э т п х величии; 1 = 1.

2. . . ., п.