Блюмин С.Л., Шуйкова И.А. Введение в математические методы принятия решений

Подождите немного. Документ загружается.

Îïðåäåëåíèå 8. Ðàçíîñòüþ íå÷åòêèõ ìíîæåñòâ íàçûâàåòñÿ ìíîæåñòâî

={õ,

À\ Â

(õ)}, õ

∈

Õ, ôóíêöèÿ ïðèíàäëåæíîñòè

ýëåìåíòîâ ê êîòîðîìó îïðåäåëÿåòñÿ êàê

À \ Â

(õ) =

=µ

& µ

(õ). (cì. ðèñ.5)

Îïðåäåëåíèå 9. Ñèììåòðè÷åñêîé ðàçíîñòüþ

íàçûâàåòñÿ ìíîæå-

ñòâî

= {<x;

À Â

(õ)>},

ãäå

À Â

(õ)=

À\ Â

(õ)

∨µ

Â\ À

(õ).

Ïðèìåð 4.

={(õ

; 0,3), (õ

; 0,8), (õ

; 0,4)},

={(õ

; 0,9), (õ

; 0,2), (õ

; 0,4), (õ

; 0,5)}.

∨

={(õ

; 0,9), (õ

; 0,2), (õ

; 0,4), (õ

; 0,5), (õ

; 0,4),}.

∧

={(õ

; 0,3), (õ

; 0,4)}.



={(õ

; 0,7), (õ

; 1), (õ

; 0,2), (õ

; 1), (õ

; 0,6), (õ

; 1)}.

={(õ

; 0,1), (õ

; 0,6), (õ

; 0,4)}.

={(õ

; 0,7), (õ

; 0,2), (õ

; 0,5), (õ

; 0,6)}.

Îïðåäåëåíèå 10. Âûïóêëîé êîìáèíàöèåé ìíîæåñòâ À

, À

,  À

íàçû-

âàåòñÿ íå÷åòêîå ìíîæåñòâî À ñ ôóíêöèåé ïðèíàäëåæíîñ-

òè

(õ) =

∑λ

(x), ãäå

≥

0, i=1, 2, 3, . n, è

∑λ

=1.

Îïðåäåëåíèå 11. Ìíîæåñòâîì óðîâíÿ α íå÷åòêîãî ìíîæåñòâà

â Õ, íà-

çûâàåòñÿ ìíîæåñòâî â îáû÷íîì ñìûñëå, ñîñòàâëåííîå èç

ýëåìåíòîâ õ

∈

Õ, ñòåïåíè ïðèíàäëåæíîñòè êîòîðûõ íå÷åò-

êîìó ìíîæåñòâó À áîëüøå èëè ðàâíû

={õ

∈

Õ,

(õ)

≥α

2.3. Îñíîâíûå ñâîéñòâà íå÷åòêèõ ìíîæåñòâ

1.  (

) ≈

èíâàëþöèÿ

∨

≈

èäåìïîòåíòíîñòü

∧

≈

∨

≈

∨

êîììóòàòèâíîñòü

∧

≈

∧

∨(

∨

)≈(

∨

)∨

≈

∨

àcñîöèàòèâíîñòü

∧ (

∧

)≈(

∧

)∧

≈

∧

∨(

∧

)≈(

∨

)∧(

∨

) äèñòðèáóòèâíîñòü

∧ (

∨

)≈(

∧

)∨ (

∧

)

6.  (

∨

) ≈ 

∧

çàêîíû äå Ìîðãàíà

 (

∧

) ≈

∨

≈

∨

∧

≈

∧

∨

∨

≈

∨

∨

∧

∧

≈

∧

∧

9. (

∨

)∨ (

∧

)≈

∨

(

∧

)∧ (

∨

)≈

∧

10.

≈

∧

11.

≈

12.

(

)≈(

)

≈

13.

≈(

)∨(

)

14. (

)≈(



)

15. (

)≈(

)

16. (

(

∨

))≈((

∧

)

17. ((

∧

)

(

∨

))≈((

∧

)

(

∨

)

18.

∨∅≈

∧∅≈∅

19.

∨Õ≈Õ

∧Õ≈

Ïåðå÷èñëåííûå âûøå îñíîâíûå ñâîéñòâà íå÷åòêèõ ìíîæåñòâ åùå

íå ÿâëÿþòñÿ ñèñòåìîé àêñèîì. Ñòðîãàÿ æå ñèñòåìà àêñèîì, àäåêâàòíàÿ, â

÷àñòíîñòè, àëãåáðå íå÷åòêèõ ìíîæåñòâ áûëà ñôîðìóëèðîâàíà çà 7 ëåò äî

èõ âîçíèêíîâåíèÿ. Ñîîîòâåòñòâóþùàÿ àëãåáðàè÷åñêàÿ ñòðóêòóðà îïðåäå-

ëÿåòñÿ íà ìíîæåñòâå Õ ñ äâóìÿ ñèñòåìàìè îïåðàöèé: <Õ, +, *, , 0,1>

èëè <Õ, ∨, ∧, , 0,1>, ãäå x ∧ y=(x+ y)*y, x∨ y=(x* y)+y

(ñèìâîëû îïåðàöèé âûáðàíû äëÿ ïðîñòîòû ôîðìóëèðîâîê, èõ íå ñëåäóåò

âîñïðèíèìàòü áóêâàëüíî, êàê ñîîòâåòñòâóþùèå àðèôìåòè÷åñêèå èëè ëî-

ãè÷åñêèå îïåðàöèè).

Ñèñòåìà àêñèîì

4. Çàäà÷è ïðèíÿòèÿ ðåøåíèÿ íà áàçå íå÷åòêîé

ëîãèêè

Â [3] âûäåëÿåòñÿ íåñêîëüêî òèïîâ çàäà÷ ïðèíÿòèÿ ðåøåíèé íà áàçå

íå÷åòêîé ëîãèêè.

1. õ + y = y + x

2. x + (y + z) = (x + y) + z

3. x+

x = 1

4. x + 1 = 1

5. x + 0 = x

6. (x + y) =

x *

7. x =

(

8. 0 = 1

9. x

y = y

10. x

z)= (x

11. x + (y

z) = (x + y)

(x + z)

1'. õ * y = y * x

2'. x * (y * z) = (x * y) * z

3'. x *

x = 1

4'. x * 0 = 0

5'. x * 1 = x

6'. (x * y) =

x +

9'. x

y = y

10'. x

z)= (x

11'. x * (y

z)=(x*y)

(x * z)

Ýòà ñèñòåìà àêñèîì ïîëíà. Ïîäàëãåáðà ÂÕ òåõ ýëåìåíòîâ èç Õ, äëÿ

êîòîðûõ õ + õ = õ (èëè, ÷òî ðàâíîñèëüíî õ*õ=õ), ÿâëÿåòñÿ áóëåâîé

àëãåáðîé, â êîòîðîé x + y = x

∨

y, x*y = x

∧

Ñâÿçü ñ íå÷åòêèìè ìíîæåñòâàìè ñòàíîâèòñÿ ÿñíîé ïîñëå ðàññìîò-

ðåíèÿ êëàññà ïðèìåðîâ òàêèõ àëãåáð, îáðàçîâàííîãî ìíîæåñòâàìè S äåé-

ñòâèòåëüíûõ ÷èñåë ìåæäó 0 è 1, óäîâëåòâîðÿþùèìè óñëîâèÿì (äâîéíûå

++, -- îáîçíà÷àþò îáû÷íûå àðèôìåòè÷åñêèå îïåðàöèè):

1. 0

∈

S è 1

∈

2. åñëè x, y

∈

S, òî min(1, x++y)

∈

3. åñëè x, y

∈

S, òî max(0, x++y  1)

∈

4. åñëè x

∈

S, òî 1x

∈

Îïåðàöèè â S îïðåäåëÿþòñÿ ñëåäóþùèì îáðàçîì:

x + y = min(1, x++y), x*y = max(0, x++y  1),



x = 1 - x,

∨

y = max(x,y), x

∧

y=min(x,y).

Áåç òðóäà ïðîâåðÿåòñÿ, ÷òî òàê îïðåäåëåííàÿ ñòðóêòóðà óäîâëåòâîðÿ-

åò ïðèâåäåííûì àêñèîìàì, íî íå àêñèîìàì áóëåâîé àëãåáðû. Ñôîðìóëè-

ðîâàííûì óñëîâèÿì 1  4 óäîâëåòâîðÿþò ðàçëè÷íûå êîíêðåòíûå ìíîæå-

ñòâà, íàïðèìåð, S={0,1}; S=[0,1]; S={âñå ðàöèîíàëüíûå ÷èñëà ìåæäó

0 è 1}; S(m)={âñå ðàöèîíàëüíûå ÷èñëà âèäà n/m äëÿ íåêîòîðîãî ôèêñè-

ðîâàííîãî íàòóðàëüíîãî m è öåëûõ 0

≤

m}, ñ îïåðàöèÿìè

Íå÷åòêîå ïîäìíîæåñòâî À óíèâåðñàëüíîãî ìíîæåñòâà U ìîæåò áûòü

îïðåäåëåíî ôóíêöèåé ïðèíàäëåæíîñòè

(À,õ)

∈

Õ, ãäå Õ óäîâëåòâîðÿåò

òðåáóåìûì àêñèîìàì (òðàäèöèîííî Õ=S=[0,1]);

(U,u) = 1. Îïåðà-

öèè íàä íå÷åòêèìè ìíîæåñòâàìè îïðåäåëÿþòñÿ â òåðìèíàõ èõ ôóíêöèé

ïðèíàäëåæíîñòè è ñâîäÿòñÿ (ïîòî÷å÷íî) ê îïåðàöèÿì íàä çíà÷åíèÿì

ïîñëåäíèõ, òî åñòü ê îïåðàöèÿì â Õ.

Îïåðàöèè  , +, * â ñëó÷àå Õ=S =[0,1] è ÿâëÿþòñÿ èçâåñòíûìè â

òåîðèè íå÷åòêèõ ìíîæåñòâ äîïîëíåíèåì, ãðàíè÷íûìè ñóììîé è ïðîèçâå-

äåíèåì, ìåíåå ïîïóëÿðíûìè, ÷åì ∨, ∧, íî íàõîäÿùèìè ñâîå îáîñíîâà-

íèå â íîâîì êîíòåêñòå. Âíå ýòîãî êîíòåêñòà, (â ÷àñòíîñòè, â ðàìêàõ áóëåâîé

àëãåáðû) íåïîñðåäñòâåííóþ ñâÿçü ìåæäó îïåðàöèÿìè ∧, ∨ è  íàä íå÷åò-

êèìè ìíîæåñòâàìè óñòàíîâèòü çàòðóäíèòåëüíî.

3. Íå÷åòêèå ñîîòâåòñòâèÿ è îòíîøåíèÿ

3.1. Ñïîñîáû çàäàíèÿ íå÷åòêèõ ñîîòâåòñòâèé

Îïðåäåëåíèå 1. Íå÷åòêèì ñîîòâåòñòâèåì ìåæäó ìíîæåñòâàìè Õ è Y íà-

çûâàåòñÿ è ÷åðåç

= (Õ, Y,

) îáîçíà÷àåòñÿ òðîéêà

ìíîæåñòâ, â êîòîðîé X, Y  ïðîèçâîëüíûå ÷åòêèå ìíîæå-

ñòâà,

- íå÷åòêîå ìíîæåñòâî â ÕõY. Ïîäîáíî íàçâàíèÿì

ýëåìåíòîâ ÷åòêîãî ñîîòâåòñòâèÿ ìíîæåñòâî Õ íàçûâàþò

îáëàñòüþ îòïðàâëåíèÿ, ìíîæåñòâî Y- îáëàñòüþ ïðèáû-

òèÿ, à

 íå÷åòêèì ãðàôèêîì íå÷åòêîãî ñîîòâåòñòâèÿ.

Íàçîâåì íîñèòåëåì íå÷åòêîãî ñîîòâåòñòâèÿ

= (Õ, Y,

) ñîîò-

âåòñòâèå Ã = (X, Y, F), ó êîòîðîãî ãðàôèê F ÿâëÿåòñÿ íîñèòåëåì íå÷åòêî-

ãî ãðàôèêà

Íå÷åòêîå ñîîòâåòñòâèå ìîæåò áûòü çàäàíî òåîðåòèêî-ìíîæåñòâåí-

íî, ãðàôè÷åñêè è â ìàòðè÷íîì âèäå.

Äëÿ òåîðåòèêî-ìíîæåñòâåííîãî çàäàíèÿ íå÷åòêîãî ñîîòâåòñòâèÿ íå-

îáõîäèìî ïåðå÷èñëèòü ýëåìåíòû ìíîæåñòâ Õ è Yè çàäàòü íå÷åòêîå ìíî-

æåñòâî

â ÕõY.

Â ìàòðè÷íîì âèäå íå÷åòêîå ñîîòâåòñòâèå

= (Õ, Y,

) çàäàåòñÿ ñ

ïîìîùüþ ìàòðèöû èíöèäåíöèé R

, ñòðîêè êîòîðîé ïîìå÷åíû ýëåìåíòà-

ìè x

∈X (i∈I={1, 2, ..., n}), ñòîëáöû  ýëåìåíòàìè y

∈Y

∈

£={1, 2, ...,m}), à íà ïåðåñå÷åíèè ñòðîêè õ

è ñòîëáöà ó

ñòàâèòñÿ

ýëåìåíò r

>, ãäå m

 ôóíêöèÿ ïðèíàäëåæíîñòè ýëåìåíòîâ èç

ÕxY íå÷åòêîìó ãðàôèêó.

Íå÷åòêîå ñîîòâåòñòâèå ìîæíî çàäàòü â âèäå îðèåíòèðîâàííîãî ãðà-

ôà ñ ìíîæåñòâîì âåðøèí X

∪

Y, êàæäîé äóãå <x

, y

>, êîòîðîãî ïðèïè-

ñàíî çíà÷åíèå

> ôóíêöèè ïðèíàäëåæíîñòè.

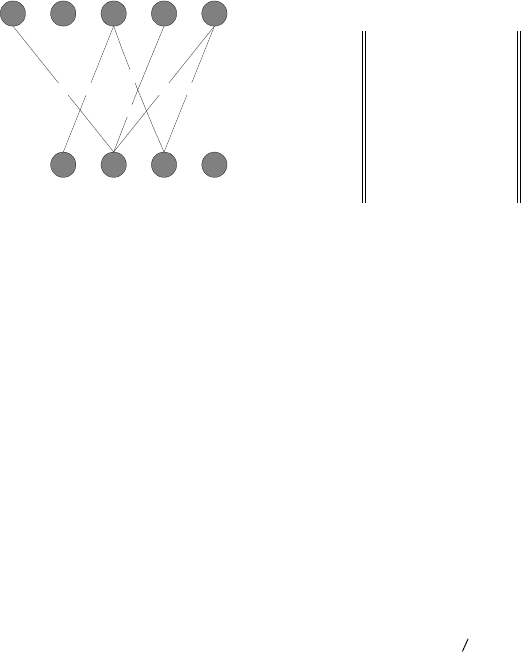
Ïðèìåð 1. Çàäàäèì íåêîòîðîå íå÷åòêîå ñîîòâåòñòâèå

= (X,Ó,

îïðåäåëèâøè X è Y êàê Õ= {õ

,õ

,...,õ

}, Y={ó

, y

={<0,2/<x

>>, <1/<x

>>, <0,4/<x

>>,

<0,3/<x

>>, <0,7/<x

>>, <0,8/<x

>>}. Ìàòðèöà

èíöèäåíöèé Rã è ãðàô íå÷åòêîãî ñîîòâåòñòâèÿ èçîáðàæåíû íà ðèñ. 6.

Ðèñ. 6 Ãðàôè÷åñêîå è ìàòðè÷íîå çàäàíèå íå÷åòêîãî ñîîòâåò-

ñòâèÿ

= (X, Ó,

Àíàëîãè÷íî ñòåïåíè ðàâåíñòâà ìíîæåñòâ ââåäåì ïîíÿòèå ñòåïåíè

ðàâåíñòâà äâóõ íå÷åòêèõ ñîîòâåòñòâèé.

Îïðåäåëåíèå 2. Ïóñòü

=(X, Ó,

∆

= (X, Ó,

)  íåêîòîðûå íå÷åò-

êèå ñîîòâåòñòâèÿ ìåæäó ìíîæåñòâàìè Õ è Y. Îïðåäåëèì

ñòåïåíü ðàâåíñòâà

(

∆

) ñ ïîìîùüþ âûðàæåíèÿ

)

(

)

(

><>↔<=∆

>∈<

XxY

µµµ

Åñëè

(

∆

) ≥ 0,5, òî áóäåì ïîëàãàòü, ÷òî ñîîòâåòñòâèÿ

∆

íå÷åòêî ðàâíû, è îáîçíà÷àòü ýòî

≈

∆

. Åñëè

(

∆

)≤

,5, òî ïîëàãà-

åì, ÷òî

∆

íå÷åòêî íå ðàâíû, è îáîçíà÷àåì ýòî

∆

. Â ñëó÷àå,

êîãäà

(

∆

)=0,5, ñîîòâåòñòâèÿ

∆

îäíîâðåìåííî íå÷åòêî ðàâíû

è íå ðàâíû, ò.å. âçàèìíî èíäèôôåðåíòíû. Ýòî îáîçíà÷àåòñÿ

∆

0,2

0,4

0,3

0,8

0,7

3.2. Îáðàç è ïðîîáðàç ìíîæåñòâà ïðè íå÷åòêîì ñîîòâåò-

ñòâèè

Äàäèì îïðåäåëåíèÿ èíâåðñèè è êîìïîçèöèè íå÷åòêèõ cîîòâåòñòâèé.

Îïðåäåëåíèå 3. Èíâåðñèåé íå÷åòêîãî ñîîòâåòñòâèÿ

= (X, Ó,

)îáî-

çíà÷àåòñÿ íå÷åòêîå ñîîòâåòñòâèå

(X,

Ó,

)

-1

, ó

êîòîðîãî ãðàôèê

-1

ÿâëÿåòñÿ èíâåðñèåé ãðàôèêà

, ìíî-

æåñòâî Y  îáëàñòüþ îòïðàâëåíèÿ, à Õ  îáëàñòüþ ïðèáû-

òèÿ.

Îïðåäåëåíèå 4. Êîìïîçèöèåé íå÷åòêèõ ñîîòâåòñòâèé

= (X, Ó,

)è

∆

= (Y, Z,

) íàçûâàåòñÿ íå÷åòêîå ñîîòâåòñòâèå

Ô =

(Õ,

)

, îáîçíà÷àåìîå

Ô =

∆

, ó êîòîðîãî

îáëàñòü îòïðàâëåíèÿ ñîâïàäàåò ñ îáëàñòüþ îòïðàâëåíèÿ

ñîîòâåòñòâèÿ

, îáëàñòü ïðèáûòèÿ  ñ îáëàñòüþ ïðèáû-

òèÿ ñîîòâåòñòâèÿ

∆

, à ãðàôèêîì

ÿâëÿåòñÿ êîìïîçèöèÿ

ãðàôèêîâ

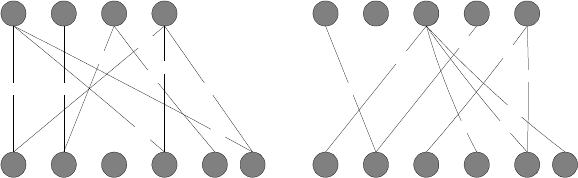
Ïðèìåð 2. Ïóñòü

∆

 íå÷åòêèå ñîîòâåòñòâèÿ, ãðàôû êîòîðûõ

îïðåäåëåíèþ êîìïîçèöèè, ïîêàçàí íà ðèñ. 6 è ðèñ. 7. Ãðàô ñîîòâåòñòâèÿ

Ô =

∆

, ïîñòðîåííîãî ïî îïðåäåëåíèþ êîìïîçèöèè, ïîêàçàí íà ðèñ. 8.

0,4

0,7

0,8

0,5

0,2

0,3

0,5

0,6

∆

0,1

0,2

0,1

0,4

0,3

0,5

0,7

Ðèñ. 7 Ãðàô íå÷åòêîãî ñîîòâåò-

ñòâèÿ

∆

Ðèñ. 8 Ãðàô íå÷åòêîãî ñîîò-

âåòñòâèÿ

Ïóñòü

= (X, Y,

) - íå÷åòêîå ñîîòâåòñòâèå, à

 íå÷åòêîå ìíî-

æåñòâî â Õ ñ ôóíêöèåé ïðèíàäëåæíîñòè

Îáðàçîì ìíîæåñòâà

ïðè ñîîòâåòñòâèè

íàçûâàåòñÿ íå÷åòêîå

ìíîæåñòâî

Ã (

)

â Y, îïðåäåëÿåìîå âûðàæåíèåì

(

Ã (

)

ã (A)

>∈

, ãäå

µµµ

ã (A)

(

)

(

)

=∨ & < >

∈

Èíà÷å ãîâîðÿ, ïîñêîëüêó êàæäûé ýëåìåíò ó

∈

Y ìîæåò ñîîòâåòñòâî-

âàòü íåñêîëüêèì ýëåìåíòàì õ

∈

À, ãäå À  íîñèòåëü ìíîæåñòâà

, òî

çíà÷åíèå ôóíêöèè ïðèíàäëåæíîñòè ýëåìåíòà ó íå÷åòêîìó ìíîæåñòâó

Ã (

)

îïðåäåëÿåòñÿ êàê íàèáîëüøåå èç çíà÷åíèé, ïîëó÷àåìûõ ñ ïîìî-

ùüþ âûáîðà ìèíèìàëüíîãî ìåæäó çíà÷åíèÿìè ôóíêöèè ïðèíàäëåæíîñ-

òè êàæäîãî õ

∈

À íå÷åòêîìó ìíîæåñòâó

è çíà÷åíèåì ôóíêöèè ïðè-

íàäëåæíîñòè ïàðû (õ, ó ) íå÷åòêîìó ãðàôèêó

. Åñëè íàõîäèòñÿ îáðàç

Ã (

)

÷åòêîãî ìíîæåñòâà À ïðè ñîîòâåòñòâèè

, òî

(

Ã (

)

ã (A)

>∈

, ãäå

µµ

ã (A)

(

)

=∪ < >

∈

Ïðèìåð 3. Ïóñòü äàíî íå÷åòêîå ñîîòâåòñòâèå

, ãðàô êîòîðîãî

èçîáðàæåí íà ðèñ. 6. Äàíî íå÷åòêîå ïîäìíîæåñòâî

={< 0,6/x1>,<0,9/x4>, <0,1/õ5>) ìíîæåñòâà X. Íåîáõîäèìî

íàéòè îáðàç

ïðè ñîîòâåòñòâèè

. Ñ ýòîé öåëüþ äëÿ êàæäîãî ó∈Ó

îïðåäåëèì çíà÷åíèå

µµµ µµ

ã (A)

(

)

(

)

(

)

= & < >∨ & < >∨

∨&<>=

(

)

µµ

;

µµµ µµ

ã (A)

(

)

(

)

(

)

= &< >∨ &< >∨

∨&<>=&∨&∨&=

(

)

(

)

(

)

(

)

µµ

=0,2∨0,3∨0,1=0,3

Ïðîäîëæàÿ àíàëîãè÷íî, íàõîäèì

ã (A)

(

)

;

ã (A)

(

)

Îáðàçîì ìíîæåñòâà

ïðè ñîîòâåòñòâèè

= (X, Y,

) ÿâëÿåòñÿ íå÷åò-

êîå ìíîæåñòâî

}

Ã (

)

0,3

>< >

Äëÿ îáðàçîâ íå÷åòêèõ ïîäìíîæåñòâ

ìíîæåñòâà Õ ïðè

íå÷åòêîì ñîîòâåòñòâèè

= (X, Y,

) ñïðàâåäëèâû ñëåäóþùèå ñâîéñòâà.

Åñëè

, òî

~ ~

Ã(À

)

~ ~

Ã(Â

)

Ã(À

)

(

)

(

)

∪≈ ∪

Ã(À

)

(

)

(

)

∩≈ ∩

Åñëè

= (X, Y,

) è

∆

= (Y, Z,

)  íå÷åòêèå ñîîòâåòñòâèÿ, à

Ô =

(Õ,

)

èõ êîìïîçèöèÿ, òî äëÿ íå÷åòêîãî ìíîæåñòâà

â Õ èìååò

ìåñòî

(

Ô(

)

(

)(

)

(

))

≈≈

∆∆

Ïî àíàëîãèè ñ ÷åòêèìè ñîîòâåòñòâèÿìè ââîäèòñÿ ïîíÿòèå ïðîîáðà-

çà íå÷åòêîãî ìíîæåñòâà ïðè äàííîì íå÷åòêîì ñîîòâåòñòâèè.

Ïóñòü

= (X, Y,

)  íå÷åòêîå ñîîòâåòñòâèå, à

 íå÷åòêîå

ìíîæåñòâî â Y ñ ôóíêöèåé ïðèíàäëåæíîñòè

. Ïðîîáðàçîì

(

)

−

ìíîæåñòâà

ïðè ñîîòâåòñòâèè

íàçûâàåòñÿ íå÷åòêîå ìíî-

æåñòâî

(

)

−

â Õ, îïðåäåëÿåìîå ñëåäóþùèì âûðàæåíèåì:

(

)

(B)

-1

−

>∈

, ãäå

µµµ

(B)

-1

(

)

(

)

=∨ & < >

∈

Íåòðóäíî çàìåòèòü, ÷òî ïðîîáðàç ìíîæåñòâà

ïðè ñîîòâåòñòâèè

ñîâïàäàåò ñ îáðàçîì

ïðè ñîîòâåòñòâèè

−

. Îòñþäà ñëåäóåò, ÷òî

ñâîéñòâà, êîòîðûìè îáëàäàåò ïðîîáðàç íå÷åòêîãî ìíîæåñòâà ïðè ñîîòâåò-

ñòâèè

, ñîâïàäàþò ñî ñâîéñòâàìè îáðàçà ýòîãî ìíîæåñòâà ïðè ñîîòâåò-

ñòâèè

−

3.3. Îñíîâíûå ñâîéñòâà íå÷åòêèõ ñîîòâåòñòâèé

Îñíîâíûìè ñâîéñòâàìè íå÷åòêèõ ñîîòâåòñòâèé ÿâëÿþòñÿ íå÷åòêàÿ

ôóíêöèîíàëüíîñòü, íå÷åòêàÿ èíúåêòèâíîñòü, íå÷åòêàÿ âñþäó îïðåäåëåí-

íîñòü, íå÷åòêàÿ ñþðúåêòèâíîñòü, íå÷åòêàÿ áèåêòèâíîñòü.

Äëÿ ÷åòêèõ ñîîòâåòñòâèé

)

(

ñâîéñòâî ôóíêöèîíàëü-

íîñòè, îïðåäåëåííîå êàê îòñóòñòâèå â ãðàôèêå F äâóõ ïàð âèäà <x, y

> è

<x, y

≠

, ìîæíî çàäàòü, èñïîëüçóÿ ïîíÿòèå ïðîîáðàçà ïðè äàí-

íîì ñîîòâåòñòâèè. Äåéñòâèòåëüíî, ñîîòâåòñòâèå

)

(

íåôóíê-

öèîíàëüíî, åñëè äëÿ êàêèõ-ëèáî äâóõ ýëåìåíòîâ y

, y

∈

Y èìååò ìåñòî

)

-1

∩≠∅

. Îòñþäà â ôóíêöèîíàëüíîì ñîîòâåòñòâèè äëÿ

ëþáûõ y

, y

∈

Y ñïðàâåäëèâî

)

-1

∩=∅

. Ýòè ðàññóæäåíèÿ

áóäåì èñïîëüçîâàòü â äàëüíåéøåì.

Ïóñòü

= (X, Ó,

)  ïðîèçâîëüíîå íå÷åòêîå ñîîòâåòñòâèå.

Çàïèøåì äëÿ êàæäîãî y∈Y íå÷åòêîå ìíîæåñòâî

(y)

-1

(y)

-1

(y)

-1

(

)

}

, ãäå

µµ

(y)

-1

(

)

=< >

, ïîñêîëü-

êó Â={y}, à

. Ïîëó÷èì ñåìåéñòâî íå÷åòêèõ ïðîîáðàçîâ âñåõ ýëå-

ìåíòîâ ïðèáûòèÿ ñîîòâåòñòâèÿ

Îïðåäåëåíèå 5. Ñòåïåíü íåôóíêöèîíàëüíîñòè ñîîòâåòñòâèÿ

áóäåì

íàçûâàòü âåëè÷èíó

(

)

fon

è îïðåäåëèì åå ñ ïîìîùüþ

âûðàæåíèÿ

αµµ

(

)

(

)))

)

fon

)

-1

=∨ ∨ &

∈∈

Èç îïðåäåëåíèÿ ñëåäóåò, ÷òî âåëè÷èíà

(

)

fon

ñîâïàäàåò ñ íàè-