Blank L., Tarquin A. Engineering Economy (McGraw-Hill Series in Industrial Engineering and Management)
Подождите немного. Документ загружается.


SECTION
3.1
Calculations for Uniform Series That Are Shifted
F=?
o
2 3
4
5 6
7
8
9
10
II
12 13
Year
10
n
A = $50
The future worth is always located in the same period as the last uniform-
series
amount
when using the F / A factor.
It
is
also important to remember that the number
of
periods n in the P / A or
F / A factor
is
equal to the number
of
uniform-series values. It may be helpful to
renumber the cash flow diagram to avoid errors in counting. Figure
3-3
shows
Figure
3-1 renumbered to determine n = 10.
As stated above, there are several methods that can be used to solve problems
containing a uniform series that is shifted. However, it is generally more conve-
nient to use the uniform-series factors than the single-amount factors. There are
specific steps that should be followed
in
order to avoid errors:
1.
Draw a diagram
of
the positive and negative cash flows.
2.
Locate the present worth or future worth
of
each series on the cash flow
diagram.
3.
Determine n for each series by renumbering the cash flow diagram.
4. Draw another cash flow diagram representing the desired equivalent cash
flow.
5. Set up and solve the equations.
These steps are illustrated below.
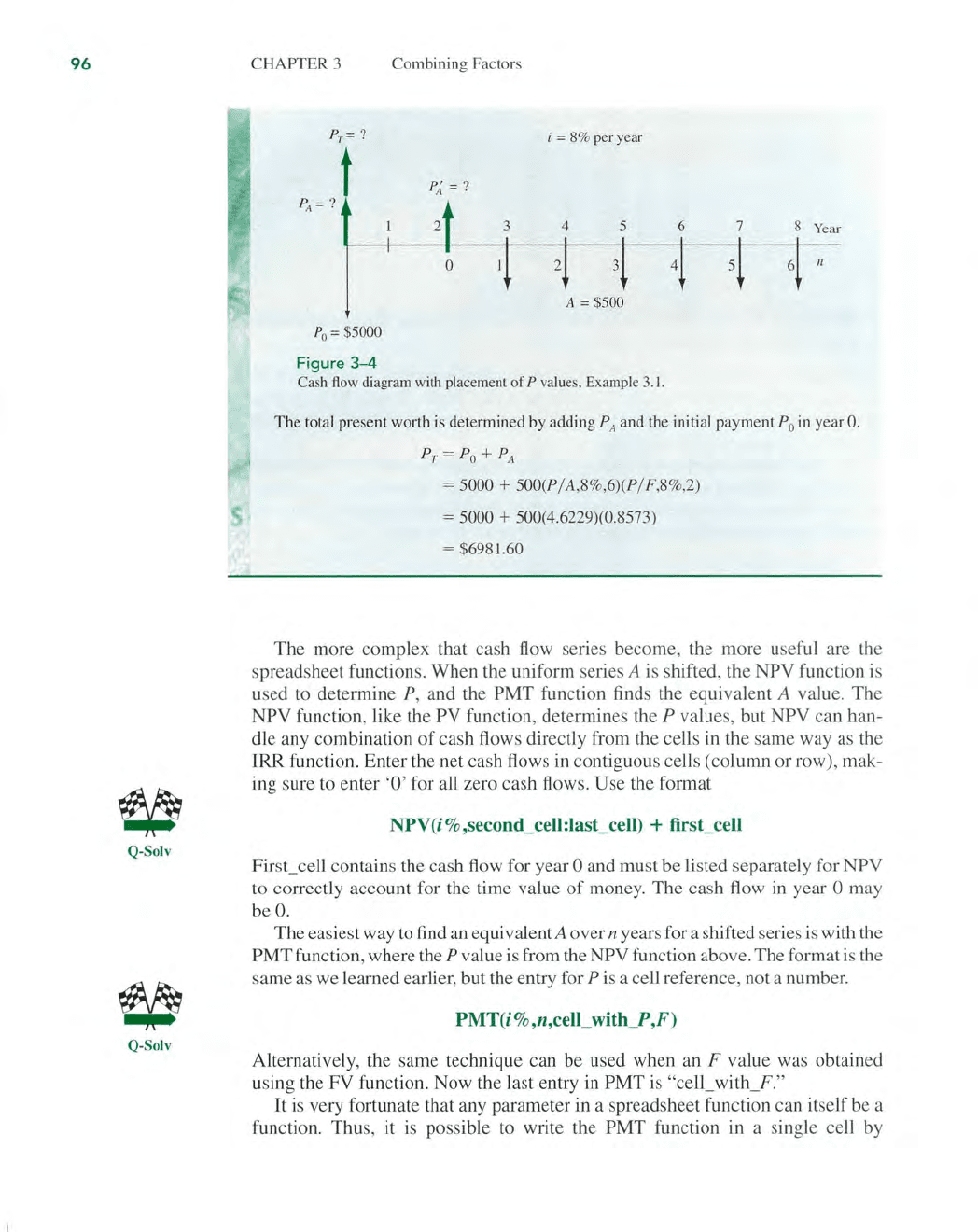
EXAMPLE 3.1
"i>
An engineering technology group
just
purchased new CAD software for $5000 now and
annual payments
of
$500 per year for 6 years starting 3 years from now for annual
upgrades. What is the present worth
of
the payments
if
the interest rate
is
8% per year?
Solution
The cash flow diagram
is
shown in Figure
3-4.
The symbol P
A
is used throughout this
chapter to represent the present worth
of
a nniform annual series A, and
P~
represents
the present worth at a time other than period
O.
Similarly, PI' represents the total present
worth at time
O.
The correct placement
of
P~
and the diagram renumbering to obtain n
are also indicated. Note that
P;
is
located
in
actual year
2,
not year
3.
Also, n = 6, not
8,
for the P / A factor. First find the value
of
P~
of
the shifted series.
P~
= $500(P / A,8%,6)
Since
P~
is located
in
year 2, now find P
A
in year O.
P
A
=
P~(P/F,8%,2)
95
Figure
3-3
Placement
of
F and
renumb
er
in
g for n for the
shifted uniform series
of
Figure
3-1.
96
Q-Solv
Q-Solv
CHAPTER 3
Po = $5000
Figure
3-4
Combining Factors
i = 8% per year
P~
=?
2 3 4 5 6 7 8 Year
A
= $500
Cash flow diagram with placement
of
P value
s,
Example 3.
1.
The
total present worth
is
determined by adding P
A
and the initial payment Po
in
year
O.
P
T
=
Po
+ P
A
= 5000 + 500(P
/A,8%,
6)(P
/F,8%,
2)
= 5000 + 500(4.6229)(0.8573)
= $6981.60
The
more complex that cash flow series become, the more useful are
th
e
spreadsheet functions. When the uniform series
A is shifted, the
NPV
function is
used to determine
P, and the
PMT
fu
n
ct
ion finds the equivalent A value. The
NPV
function, like the PV function,
det
er
mines the P values, but
NPV
can han-
dle any combination
of
cash flows directly from the cells
in
the same way as the
IRR
function. Enter the net cash flows in contiguous cells (coLumn or row), mak-
ing sure to enter
'0' for all zero cash flows. Use the format
NPV(i%,second_cell:lasCcell) + firsCcell
First_cell contains the cash flow for year 0 and must be listed
se
parately for NPV
to correctly account for the time value
of
money.
The
cash flow in year 0 may
be
O.
The
easiest way to find an equivalent A over
n.
years for a shifted series is with the
PMTfunction
, where the P va
lu
e is from the
NPV
function above. The format is
th
e
same as we learned ear
li
er
, but the entry for P is a cell reference, not a number.
PMT(i
% ,n,ceIC
with_P,F)
Alternatively, the same technique can be used when an F value
wa
s obtained
using the
FV
function.
Now
the last entry in
PMT
is
"ceILwith_F."
It
is
very fortunate that any parameter in a spreadsheet function can its
elf
be a
function. Thus, it is possible to write the
PMT
function
in
a single cell by
S
EC
TION 3
.1
Calculations for Uniform Series That Are Shifted
embedding
th
e NPY function (and FY function,
if
needed). The format is
PMT(i%,n,NPV(i%,second_cell:lasCcell)+firsCcell,F)
Of
course,
th
e answer for A is the same for the two-cell operation or a single-cell,
embedded funct
io
n.
All
three
of
these functions are illustrated in the next example.
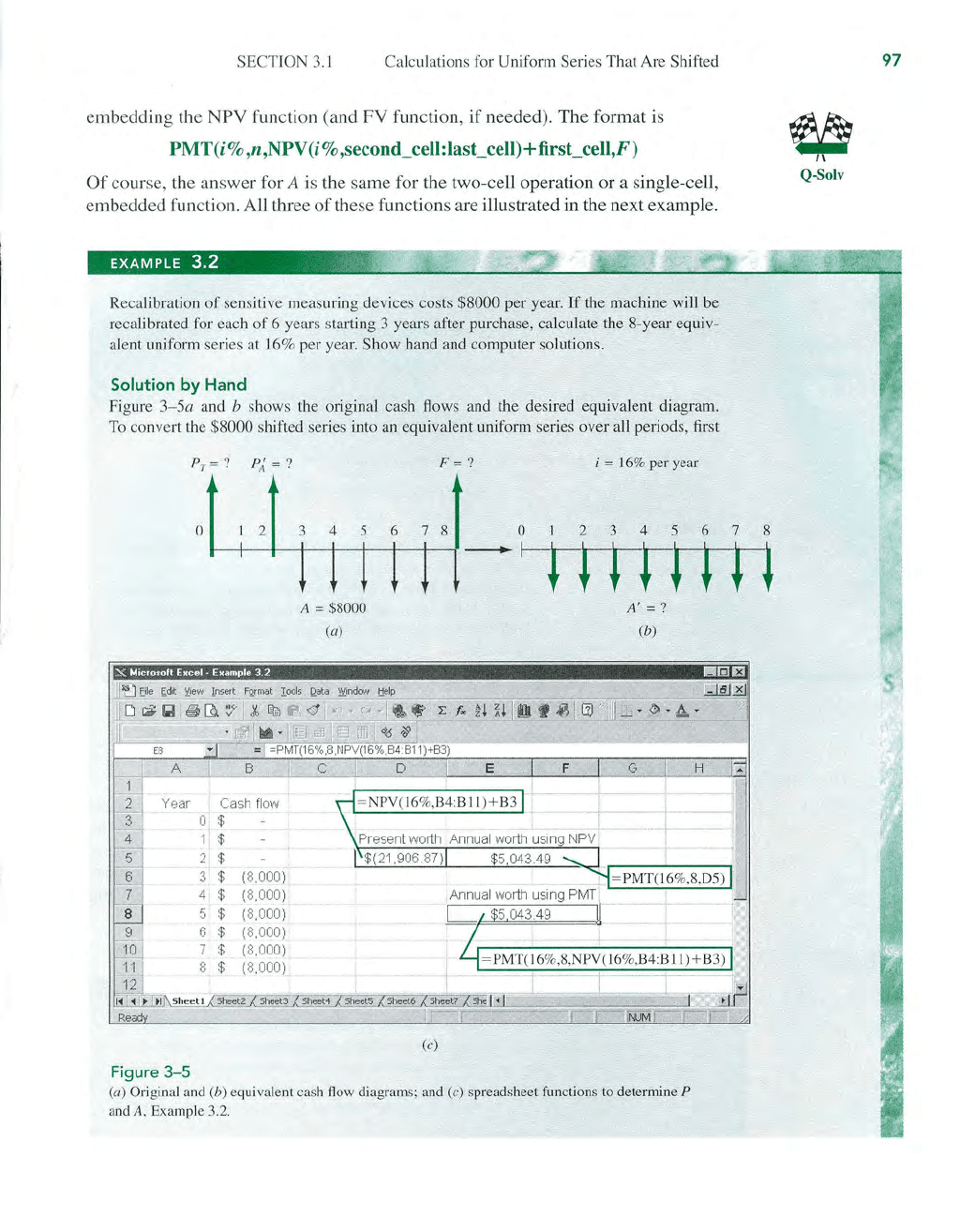
Recalibrat.ion
of
sensitive measuring devices costs $8000
per
year.
If
the machine will be
recalibrated for each
of
6 years starting 3 years after purchase, calculate the 8-year equiv-
alent uniform series at 16% per year. Show hand and computer solutions.
Solution by Hand
Figure
3- 5a and b shows the original cash flows and the desired equivalent diagram.
To
convert the $8000 shifted series into an equivalent uniform series over all periods, first
o
0
1
2
3
4
5
6
7
8
Figure
3-5
P
' -
r,
A - •
I 2
Cash f
lo
w
$
$
$
$
(8,000)
$
(8,000)
$
(8,000)
$
(8,000)
$
(8,000)
$
(8,000)
F=?
i = J 6% per year
3
45678
0
2345678
A = $8000
(a)
(e)
-
tT~
lllll
A'
=?
(b)
(a)
Original and (b) equivalent cash flow diagrams; and (e) spreadsheet functions to determine P
and
A,
Example 3.2.
97
Q-Solv

98
Q-Solv
CHAPTER
3
Combinin
g
Factor
s
convert
the uniform series into a present worth
or
future worth amount. then either the AI P
factor
or
the A I F factor can
be
used.
Both
methods
are illustrated here.
P,resent worth method.
(Refer
to
Figure
3- Sa.)
Calculate
P
~
for the shifted series
in
year
2 and
P
T
in
year
O.
p;\ = 8000(P I A, 16%,6)
P T =
P
~
(PI F, 16%,2) = 8000(P l A,
16
%,6)(P I
F,
16
%,2)
= 8000(3.
6847)(0.7432
) = $
21
,907.75
The
equivalent
series A I
for
8 years
can
now be determined via the Al P factor.
A'
= P
T
(A
IP,16%,8) = $5043.60
Future
worth method.
(Refer
to
Figure
3- Sa.)
First
calculate
thefuture
worth F
in
ye
ar
8.
F =
8000(FIA,16
%,6) =
$71,820
The
AI
F
factor
is now used to obtain
A'
over
all 8 years.
A' =
F(AIF
,16%,8) = $5043.20
Solution
by
Computer
(Refer to
Figure
3- Sc.)
Enter
the cash flows in
B3
through B
II
with entries
of
'0'
in
the
fir
st
three cells. Enter
NPV(16
%
,B4:Bll)+B3
in cell DS to display the P
of
$21,906.87.
There
are two ways to obtain the
equivalent
A
over
8 years.
Of
cour
se,
only
one
of
th
es
e
PMT
functions needs to
be
entered.
Either
enter
the
PMT
function making
dir
ec
t r
efe
ren
ce
to the
NPY
v
alue
(
se
e
cell
tag for EIFS),
or
embed
the
NPY
function
int
o the
PMT
func
ti
on
(s
ee
cell tag for EIF8
or
the
formula
bar
).
3.2
CALCULATIONS INVOLVING UNIFORM-SERIES
AND
RANDOMLY PLACED SINGLE
AMOUNTS
When a cash flow includes both a uniform series and randomly
pl
aced single
amollnts, the procedures
of
Section 3.] are applied to the uniform series a
nd
th
e
single-amount formulas are applied to the one-time cash
fl
ows. This approach,
illustrated in Examples 3.3 and 3.4,
is
merely a combination
of
previo
ll
s ones.
For spreadsheet solutions, it
is
necessary
to
enter the net cash flows before us
in
g
the
NPY and other functions.
EXAMPLE
3.3 .
An engineering
company
in Wyoming that
owns
50
hectares
of
valuable land has d
ec
ided
to lease the mineral rights to a
mining
company
.
The
primary objective is to
obt
a
in
long-
term income to finance ongoing projects 6 and 16
year
s from the pres
ent
time.
Th
e engi-
neering
company
makes a proposal to
the
mining
company
that
it
pay
$2
0,
00
0 per
yea
r
for
20
years beginning 1
year
from now, plus $
10
,
000
six years from now and $
15
,
000
SECTION 3
.2
Calculations Involving Uniform-Series and Single Amounts
sixteen years from
now.
If
the mining company wants to
payoff
its lease immediately,
how much should it pay now if the investment should make 16% per year?
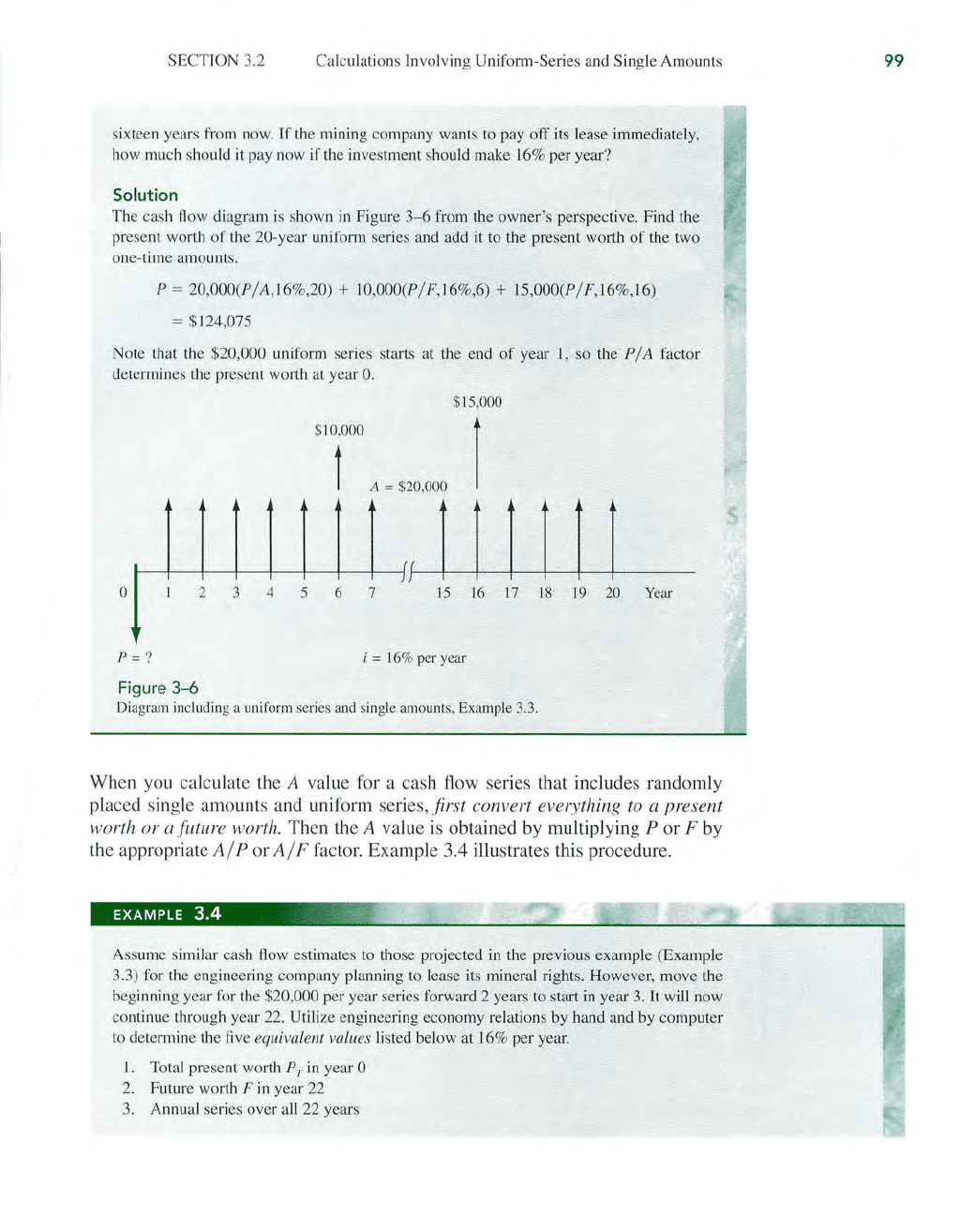
Solution
T
he
cash flow diagram is shown in Figure
3-6
from the owner's perspective. Find the
present worth of the 20-year uniform series and add it to the present worth
of
the two
one-time amounts.
P = 20,000(P/A,16%,20) +
1O
,000(P/F,16%,
6)
+ 15,000(P/F,16%,
16)
= $124,075
Note that the
$20,000 uniform series starts at the end
of
year 1, so the P / A factor
determines the present worth at year
O.
$15,000
$10,000 1
t A = $20,000
J 1 1 1 1 1 1
(
)
o
1
2 3
4
5
6
7
15
16
17 18 19
20 Year
p=?
i =
16
% per year
Figure
3-6
Diagram incJucllng a uniform series
ancl
single amounts, Example 3.3.
When you calculate the A value for a cash flow series that includes randomly
placed
single amounts a
nd
uniform series, first convert everything
to
a present
worth
or
a future worth. Then the A value is obtained by multiplying P or F by
the appropriate
AI
P or
AI
F factor. Example 3.4 illustrates this procedure.
EXAMPLE
3.4
",
Assume similar cash flow estimates
to
those projected in the previous example (Example
3.3) for
th
e engineering company planning to lease its mineral rights. However, move the
beginning y
ea
r for the $20,000 per year series forward 2 years to start in year 3. It will now
continue through year 22. Utilize engineering economy relations by hand and by computer
to
determine the five equivalent values listed below at 16% per year.
I. Total present worth P
T
in year 0
2. Future worth F
in
year 22
3. Annual ser
ie
s over all 22 years
99
100
CHAPTER 3 Combining Factors
4.
Annual series over the first 10 years
5. Annual series over the last
12
years
Solution by Hand
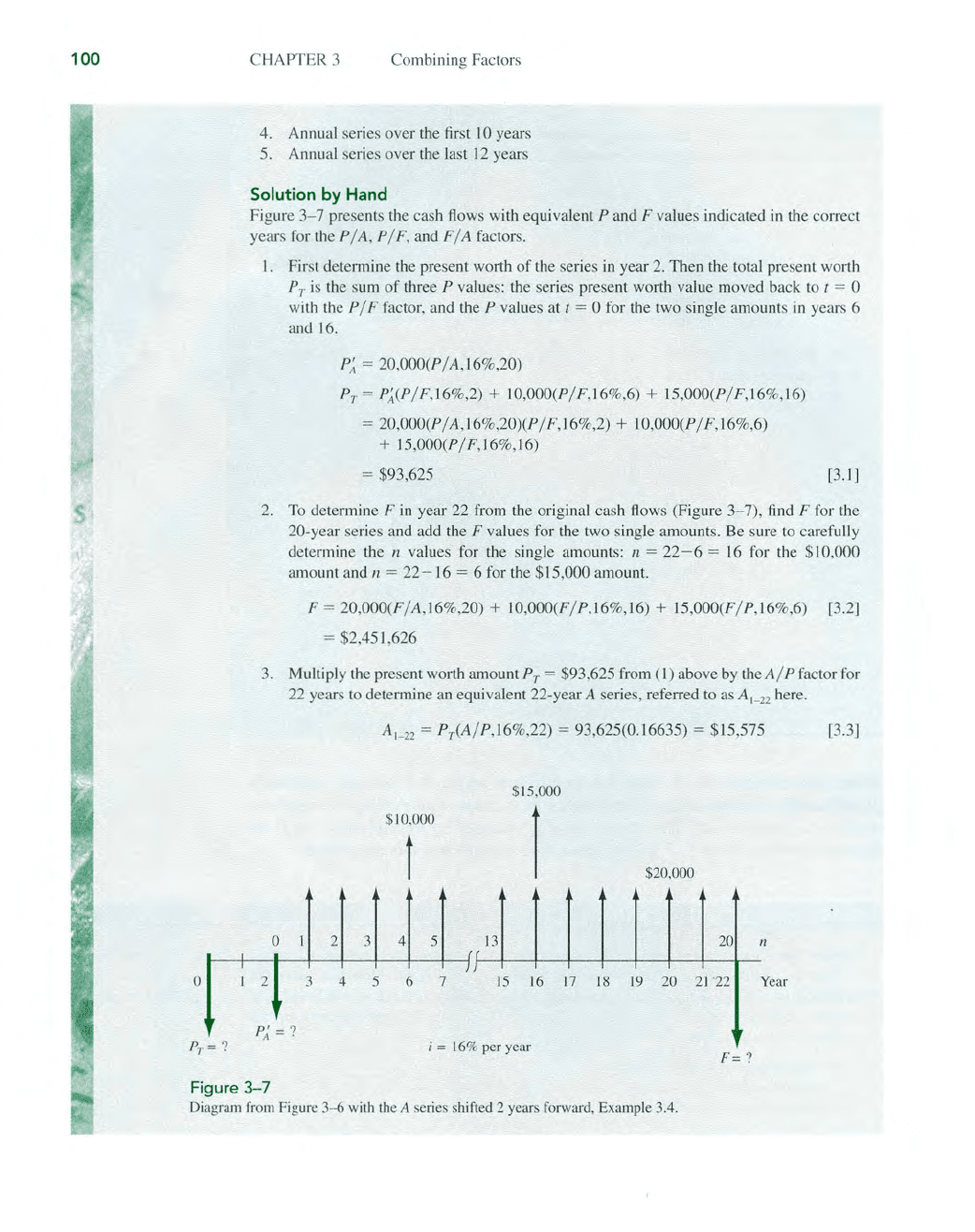
Fi
gure
3-
7 presents the cash flows with equi
va
lent P a
nd
F values indicated in the correct
y
ea
rs for the PIA, PI F, a
nd
F I A factors.
1.
First detennine the present worth
of
the series
in
year 2. Then tbe total present worth
P
T
is
the sum
of
three P values: the series present worth value moved back to t = 0
with
th
e PI F factor, and the P values at t = 0 for the two single amo
un
ts
in
years 6
a
nd
16.
P~
= 20,000(PIA,
16
%,
20)
P7'
=
P
~
(PIF
,
16%,2)
+ 10,000(PIF,16%,6) + 15,000(PIF,16
%,
1
6)
= 20,000(PIA, I
6%
,20)(PIF,16%,2) + 10,000(PIF,16
%,
6)
+ J5,000(PIF,16%,
J6)
= $93,625 [
3.
1]
2.
To
determine F
in
year
22
from the original cash flows
(F
igure 3-7),
find
F for the
20-year series and add the
F
val
ues for
th
e two single amount
s.
Be sure to carefully
determine the
n values for the
si
ngle amounts: n = 22
-6
=
16
for the $
10
,000
amount and n = 22-
16
= 6 for the $
15
,000 amou
nt.
F = 20,000(FIA, 16%,20) +
LO,000(F
I
P,l6
%,J6) + 15,000(FIP,16%,6)
[3
.
2]
= $2,45 J ,626
3.
Multiply the present worth amount P 7' = $93,625 from (I) above by the AI P factor for
22 years to detennine
an
equivalent 22-year A series, referred to
as
A 1
-22
here.
A
I
_
22
= P
T
(A
IP,
J6
%,
22) = 93,625(0.16635) = $15,575 [3.3]
$15,000
$ 10,000
1
$20,000
t
o 2
3
4 5
13
20 n
(
J
J
4
5
6 7
15
16
17
18
19 20
21'22
Year
i = l6% per yeal
F=
?
Figure
3-7
Diagram from
Fi
gure
3-
6 with
th
e A series shifted 2 years forward, Example 3.4.
SECTION 3.2 Calculations Involving Uniform-Series and Single Amounts
An alternate way to determine the 22-year series uses the
F value from (2) above. In
this case, the computation
is
A
I
_
22
= F(A/F,16%,22) = $15,575. Note that in both
methods, the equivalent total
P or F value
is
determined first, then the
A/
P or
A/
F
factor for
22
years
is
applied.
4.
This and (5), which follows, are special cases that often occur
in
engineering economy
studies. The equivalent A series
is
calculated for a number of years different from that
covered
by
the original cash flows. This occurs when a defined study period or plan-
ning horizon
is
preset for the analysis. (More
is
mentioned about study periods later.)
To
determine the equivalent A series for years 1 through
10
only (call
itA
I
_
IO
) the P
T
value must be used with the
A/
P factor for n =
10.
This computation will transform
the original cash flows
in
Figure 3- 7 into the equivalent series A
I
_
IO
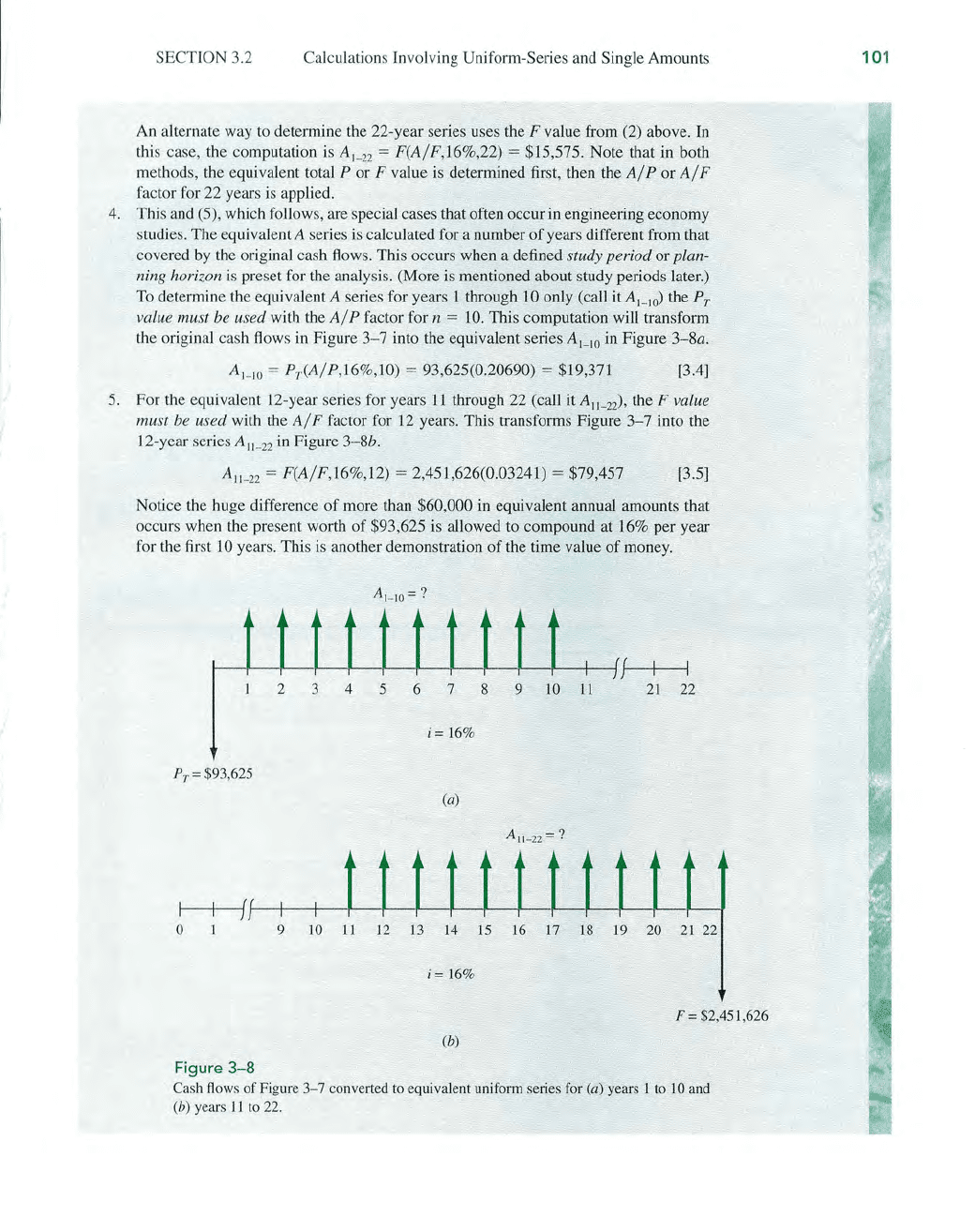
in Figure 3-8a.
A
I
_
IO
= P
T
(A/P,16%,IO) =
93
,625(0.20690) = $19,371 [3.4]
5.
For the equivalent 12-year series for years
11
through 22 (call it
AI
1
-2
2)'
the F value
must be used
with the
A/F
factor for 12 years. This transforms Figure
3-7
into the
12-year series A
11
-
22
in
Figure 3-8b.
A
II
_
22
= F(A/F,16%,12) = 2,451,626(0.03241) = $79,457 [3.5]
Notice the huge difference
of
more than $60,000
in
equivalent annual amounts that
occurs when the present worth of $93,625 is allowed to compound at 16% per year
for the first
10
years. This is another demonstration
of
the time value of money.
I
--
+
----
f
--
+t
--
t
t---+--
t t
t---+--
t t
t---+--
t t
t--t-----Jf
)f------t------j!
2 3 4 5 6 7 8 9
10
11
21
22
;=16%
P
T
= $93,625
(a)
A
II
_
22
=?
!
)
o 9
10
11
12
13
14
15 16 17
18
19
20
21
22
;=
16%
F = $2,451,626
(b)
Figure 3- 8
Cash
flow
s
of
Figure
3-7
convected to equivalent uniform series for (a) years 1 to
10
and
(b) years
11
to 22.
10
1

102
~
E-Solve
CHAPTER 3 Combining Factors
Solution by
Computer
Fi
g
ur
e
3-9
is a spreadsheet
im
age with answers for a
ll
fi
ve
questions. The $20,000 se
ri
es
a
nd
th
e two s
in
gle amounts have b
ee
n entered into separa
te
columns, B a
nd
C. The ze
ro
cash
fl
ow
va
lu
es are a
ll
entered so
th
at
th
e f
un
ct
ions will work correc
tl
y. This is an exce
l-
lent exa
mpl
e demonstrating
th
e ver
sa
tili
ty
of the NPY,
FY
, and
PMT
function
s.
In o
rd
er to
prepare for sens
iti
vi
ty
analysis,
th
e func
ti
ons are developed us
in
g ce
ll
referen
ce
fo
rm
at or
global
va
ri
a
bl
es,
as
indicated in
th
e ce
ll
tags. This m
ea
ns that virtua
ll
y any number-
th
e
in
-
terest rate, any cash
fl
ow estimate
in
tb
e se
ri
es or
th
e s
in
gle
am
ounts, a
nd
th
e timing within
th
e 22-year time fram
e-ca
n be changed a
nd
th
e new answers w
ill
be imme
di
ately
di
s-
played. This is
th
e general spreadsh
ee
t struc
tw-
e utilized for per
fo
rming an eng
in
eer
in
g
economy anal
ys
is with sensitiv
it
y anal
ys
is on the estimates.
1. Prese
nt
wo
rth va
lu
es for
th
e se
ri
es a
nd
s
in
gle amounts are det
er
min
ed
in
ce
ll
s E6 a
nd
E I 0, respective
ly
, us
in
g the NPY f
un
c
ti
on. The s
um
of
th
ese in
El
4 is P
-r
= $93,622,
whi
ch correspo
nd
s to the va
lu
e
in
E
qu
a
ti
on [3.1].
X Microsoft
Excel-
Example
3.4
I!!lliIm
'li
ew
!.n
sert
FQ!'m
at Io
ol
s
Q.,
3t
a
'6!'
ind
ow
Dl
3
A
B o E F G H
K -
Interest
rate
l6
.o
ax
•
Cash
flows
Year
S€'Ii€'s
Sin
Ie
Results
from
functions
$ $
Present
worth
$ $
of
series
=
$88,122
=NPV(DI
,B6:B27)+
BS
2
t
$
3
$
20.000
$
4
t
20
.0
00
$
Pres-eont
worth
$
20,000
$
of
singles
=
$5,500
11
$
20,000
$
10,000
12
7
$
20,000
$
13
8
$
20,000
$
1.
Present
\,lOuh
14
9
$
20,000
$
total:
$
93,622
15 10
$
20,000
$
16
11
$
20,000
$
12
$
20,000
$
2.
Futu
re
\'lOrth
13
$
20,000
tot
al
=
2,451,621
=F
V(D I
,22,0,-E
I4
)
14
$
20,000
15
$
20,000
3.
'o
.n
nu
al
series
16
$
20,000 15,000
a
m.
(22
~
rs)
~
=P
MT(Dl
,22,-E
I4)
17
$
20,000
18
$
20,000
4.
Annu.:.
1
seriE's
19
$
20,000 for f
ir
st
10
yrs
=
$
= PMT(D I, I 0, - E14)
20
20,000
20,000
5.
Annua
l
series
= PMT(D I,1
2,0,-E
I
8)
Figure
3-9
Spreadsheet
lI
s
in
g ce
ll
reference formal, Exam
pl
e 3.4.

SECTION 3.3 Calculations for Shifted Gradients
2. The
FV function
in
cell
EI8
uses the P value
in
E14 (preceded by a minus sign)
to
determine F twenty-two years later. This
is
significantly easier than Equation [3.2],
which determines the three separate
F values and adds them
to
obtain F = $2,451,626.
Of
course, either method
is
correct.
3.
To
find
the 22-year A series
of
$15,574 starting
in
year I, the PMT function in E21
references the
P value
in
cell E14. This
is
effectively the same procedure used in
Equation [3.3] to obtain
A 1- 22'
For the spreadsheet enthusiast,
itis
possible to find the 22-year A series value
in
E2l
directly
by
using the PMT function with embedded NPV functions. The cell reference
format would be
PMT(D]
,22,-(NPV(D
I,B6:B27)+B5 + NPV(Dl,C6:C27)+C5)).
4.
and
5.
It
is
quite simple to determine
an
equivalent uniform series over any number
of
periods using a spreadsheet, provided the series starts one period after the P value
is
located or ends
in
the same period that the F value
is
located. These are both true for
the series requested
here-the
first lO-year series can reference P
in
cell E14, and the
last l2-year series can anchor on
F in cell
EI8.
The results
in
E24 and E27 are the
same
as
A
I
_
IO
and A
11
- 22
in
Equations [3.4) and [3.5], respectively.
Comment
Remember that some round-otf error will always be present when comparing hand and
computer results. The spreadsheet functions carry more decimal places than the tables dur-
ing calculations. Also, be very carefnl when constructing spreadsheet functions. It
is
easy
to miss a value, such
as
the P or
Fin
PMT and FV functions, or a minus sign between
entries. Always check your function entries carefully before touching
<Ente
r
>.
Additional Example 3.10.
3.3
CALCULATIONS FOR SHIFTED GRADIENTS
In Section 2.S, we derived the relation P =
G(P/G,i,n)
to determine the present
worth
of
the arithmetic gradient series.
The
P / G factor, Equation [2.1S], was
derived for a present worth in year
0 with the gradient starting between periods
I and
2.
The
present worth
of
an
arithmetic
gradient
will always be located two
periods before the gradient starts.
Refer to Figure
2-13
as a refresher for the cash flow diagrams.
The relation A =
G(A/
G,i,n) was also derived in Section 2.S.
TheA/
G factor in
Equation [2.17] performs the equivalence transformation
of
a gradient only into an
A series from years 1 through n, as indicated in Figure
2-14.
Recall that when there
is
a base amount, it and the arithmetic gradient must be treated separately. Then the
equivalent
P or A values can be summed to obtain the equivalent total present
worth
P
T
and total annual series
AT'
according to Equations [2.18] and
[2
.19].
A conventional gradient series starts between periods 1 and 2
of
the cash flow
sequence. A gradient starting at any other time
is
called a shifted gradient. The
n value
in
the
PIG
and
A/G
factors for a shifted gradient is determined by
103
104
CHAPTER 3 Combining Factors
renumbering the time scale. The period in which the gradient .first appears is
label
ed
period 2. The n value for the factor is determined
by
the renumbered
period where the last gradient increase occurs.
Partitioning a cash flow series into the arithmetic gradient series and the
remainder
of
the cash flows can make very clear what the gradient n value should
be. Example 3.5 illustrates this partitioning.
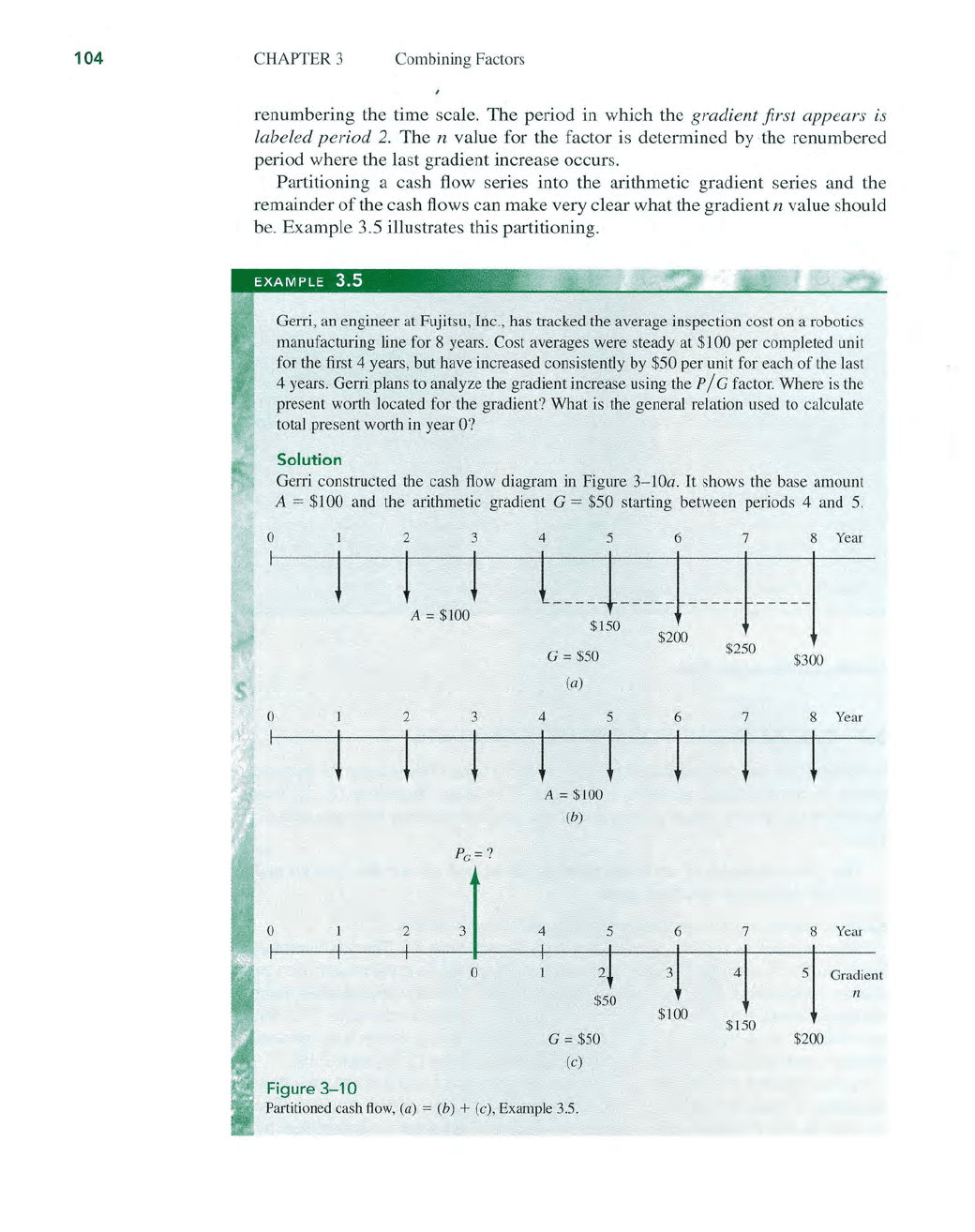
EXAMPLE 3.5
W!~
0
I
0
I
0
I
Gerri,
an
engineer at Fujitsu, Inc., has tracked the average inspection cost on a robotics
manufacturing line for 8 years. Cost averages were steady at
$100 per completed unit
for the first 4 years, but have increased consistently
by
$50 per unit for each
of
the last
4 years. Gerri plans to analyze the gradient increase using the
P / G factor. Where
is
the
present worth located for the gradient? What is the general relation used
to
calculate
total present worth
in
year
O?
Solution
Gerri constructed the cash
flow
diagram in Figure 3-
lOa
. It shows the base amount
A = $100 and the arithmetic gradient G = $50 starting between periods 4 and
5.
2 3
1
1
t
A = $100
2
3
1 1
1
Pc=
?
2
3
I
0
4
5
6
7
8
Year
t
--
-
-1--
-
-l-
-
--l-
-
--
-I
$150
$200 $250
G = $50 $300
(a)
4
5
t 1
A = $100
4
(b)
5
2+
$50
G = $50
(e)
6
t
6
3
$100
7
8
Year
t t
7 8 Year
4
5 Gradient
n
$150
$200
Figure
3-10
Partitioned cash flow, (a) = (b) + (e), Example 3.5.
