Blank L., Tarquin A. Engineering Economy (McGraw-Hill Series in Industrial Engineering and Management)
Подождите немного. Документ загружается.


LEARNING OBJECTIVES
Purpose:
Make
economic calculations
for
interest rates and
cash
flows that occur on a
time
basis other than 1 year.
No
minal and effective
Effective
annual interest rate
Effective
in
terest rate
Compare
PP
and
CP
Si
ngle amounts:
PP
;;;,
CP
Series:
PP
;;;,
CP
Single a
nd
se
ries:
PP
< CP
Continuous compounding
Varying rates
This c
hapter
wi
ll
help you:
1. Underst
and
no
min
al and e
ff
ect
ive interest rate stateme
nt
s.
2.
Derive
and
use
the
formula
for
the
effectiv
e annual
i
nterest
rate.
3.
Det
ermine
the
effective
interest rate
for
any time pe
ri
od.
4. De
te
rmine
th
e
co
rrect m
et
hod
for
equi
valence
ca
lcul
at
ions
for
diffe
re
nt payme
nt
and
compo
und
ing
period
s.
5.
Make
equivalence
ca
lculations
for
payment
periods
equal
to
or
longer
than
the
compounding
period
when
only
single
amounts
occur
.
6.
Make
equivalence
calculations
when
uniform
or
gradi
e
nt
series
occur
for
payment
periods
equal
to
or
longer
than
th
e
co
mp
o
und
ing p
er
iod.
7.
Make
equ
i
va
lence calculations
for
paym
ent
pe
ri
ods
sh
orte
r
than
th
e
co
mp
o
unding
period.
8.
Ca
lculate and use an
effective
interest
rate
for
continuou
s
compo
u
nding
.
9.
A
ccount
for
in
terest
rates
that
vary
over
time
when
performing
equivalency
computat
ions.

126
CHAPTER 4
Nominal and Effective Interest Rates
4.1
NOMINAL
AND
EFFECTIVE INTEREST
RATE
STATEMENTS
In Chapter 1, we learned that the primary difference between simple interest and
compound interest is that compound interest includes interest on the interest
earned in the previous period, while simple does not. Here we discuss nominal
and
effective interest rates, which have the same basic relationship. The differ-
ence here is that the concepts
of
nominal and effective must be used when inter-
est
is
compounded more than once each year.
For
example,
if
an interest rate
is
expressed as 1 % per month, the terms nominal and effective interest rates
mu
st
be considered.
To understand and correctly handle effective interest rates is important in en-
gineering practice, as well
as
for individual finances. Engineering projects, as
discussed in Chapter 1, are funded by capital raised through debt and equity
financing. The interest amounts for loans, mortgages, bonds, and stocks are
based upon interest rates compounded more frequently than annually. The eng
i-
neering economy study must account for these effects. In our own personal
finances, we manage most cash disbursements and receipts on a nonannual time
basis. Again, the effect
of
compounding more frequently than once per year
is
prese
nt.
First, consider a nominal interest rate.
Nominal interest rate, r, is
an
interest
rate
that
does
not
include any con-
sideration
of
compounding. By definition,
r = interest
rate
per
period x
number
of
periods [4.1]
A nominal rate r may be stated for any time
period-l
year, 6 months, quarter,
month, week, day, etc. Equation [4.1] can be used to find the equivalent
r for any
other shorter or longer time period.
For
example, the nominal rate
of
r = 1.5%
per month
is
the same as each
of
the following rates.
r = 1.5% per month X 24 months
= 36% per 2-year period
=
l.5
% per month X 12 months
= 18% per year
= 1.5% per month X 6 months
= 9% per semiannual period
= 1.5% per month X 3 months
= 4.5% per quarter
= 1.5% per month X 1 month
= 1.5% per month
= 1.5% per month X 0.231 month
= 0.346% per week
(longer than 1 month)
(longer than
I month)
(longer than 1 month)
(longer than 1 month)
(equal to 1 month)
(shorter than 1 month)
Note that none
of
these nominal rates make mention
of
the compounding fre-
quency. They all have the format
"r%
per time period t."

SECTION 4.1 Nominal and Effective Interest Rate Statements
Now, consider an effective interest rate.
Effective interest rate is
the
actual
rate
that
applies for a
stated
period of
time. The compounding
of
interest
during
the
time period
of
the corre-
sponding nominal
rate
is accounted for by the effective interest rate.
It
is
commonly expressed on
an
annual
basis as the effective
annual
rate
i
a
,
but
any
time basis can be used.
An effective rate has the compounding frequency attached to the nominal rate
statement.
If
the compounding frequency is not stated, it is assumed to be the
same as the time period
of
r,
in which case the nominal and effective rates have
the same value. All the following are nominal rate statements; however, they will
not have the same effective interest rate value over all time periods, due to the
different compounding frequencies.
4% per year, compounded monthly (compounding more often than
time period)
12% per year, compounded quarterly ( compounding
more often than
time period)
9% per year, compounded daily ( compounding more
often than
time period)
3% per quarter, compounded monthly (compounding
more often than
time period)
6% per 6 months, compounded weekly (compounding more often
than
time period)
3% per quarter, compounded daily
(compounding more often than
time period)
Note that all these rates make mention
of
the compounding frequency. They
all have the format
"r% per time period
t,
compounded m-Iy."
The
m is a month,
a quarter, a week,
or
some other time unIt. The formula to calculate the effective
interest rate value for any nominal or effective rate statement is discussed in the
next section.
All the interest formulas, factors,
tabulated
values,
and
spreadsheet rela-
tions
must
have the effective interest
rate
to
properly
account for
the
time
value
of
money.
Therefore, it
is
very important to determine the effective interest rate before
performing
ti
me val ue
of
money calculations in the engineering economy
study. This
is
especially true when the cash flows occur at other than annual
intervals.
The
terms
APR
and
APY
are used in many individual financial situations
instead
of
nominal and effective interest rates.
The
Annual Percentage Rate (APR)
is
the same as the nominal interest rate, and Annual Percentage Yield (APY) is
used
in
lieu
of
effective interest rate. All definitions and interpretations are the
same
as
those developed in this chapter.
127

128
CHAPTER 4 Nominal and Effective Interest Rates
Ba
se
d
on
these descriptions, there
are
always three
time-based
units associ-
ated with an interest rate statement.
Time
period-the
period
over
which
the interest is expressed.
This
is
the
t
in
the
statement
of
r%
per
time period
t,
for example, 1 %
per
month.
The
time unit
of
1 year is by far the
most
common.
It
is
assumed
when not stated otherwise.
Compounding
period
(CP)-the
shortest
time
unit
over
which interest
is
charged
or
earned.
This
is defined
by
the
compounding
term in the interest
rate statement,
for
example,
8%
per
year
compounded monthly.
If
not
stated, it
is
assumed
to
be
1 year.
Compounding
frequency-the
number
of
times that m
compounding
occurs
within the
time
period
t.
If
the
compounding
period
CP
and the time period
t
are
the
same,
the
compounding
frequency
is 1,
for
example,
1%
per
month compounded monthl
y.
Consider
the rate
8%
per
year,
compounded
monthly.
It
has a
time
period I
of
1
year
, a
compounding
period
CP
of
1 month, and a
compounding
frequency
m
of
12
times
per
year. A rate
of
6%
per
year,
compounded
weekly, has t = 1 year,
CP
= 1
week
, and m = 52, based
on
the standard
of
52
weeks
per
year.
In previous chapters, all interest rates
have
t
and
m values
of
1 year. This
means the rates are both
the
effective and the
nominal
rate
because
the
same
time
unit
of
1
year
is used.
It
is
common
to express the effective rate on
the
same
time
basis as the
compounding
period.
The
corresponding
effective
rate
per
CP
is
determined
by using the relation
r%
per
time period t
Effective
rate
per
CP
=
-----=---.---=-----
m compoundmg periods
per
t
r
m
[4.2]
As an illustration,
assume
r = 9%
per
year
,
compounded
monthly;
then m =
12.
Equation
[4.2] is u
se
d to obtain the effective rate
of
9%/12
= 0.75%
per
month,
compounded
monthly. It is
important
to note
that
changing
the basic time pe-
riod
I
does
not
alter
the
compounding
period, which
is
1
month
in this illustration.
The different bank loan rates for three separate electric generation equipment projects are
listed below. Determine tbe effective rate
on
the basis
of
the compounding period for each
quote.
(0) 9% per year, compounded quarterly.
(b) 9% per year, compounded monthly.
(c) 4.5% per 6-montbs, compounded weekly.
Solution
Apply Equation [4.2] to detemllne the effective rate per
CP
for different compounding
frequencies. The accompanying graphic indicates bow the interest rate
is
distributed over
time.

SECTION
4.1
Nominal and Effective Interest Rate Statements
Effective
Nominal
Compounding
Rate
r%
per
t
Period
m
perCP
Distribution
Over
Time Period t
(a)
9% per year Quarter 4 2.25%
2.25% 2.25% 2.25% 2.25%
2
3 4
(b) 9% per year Month
12
0.75%
~O.173%~
(c) 4.5% per
6-months
Week
26
0.173%
111111111111111111111111111
12
14
16
Sometimes
it
is
not obvious whether a stated rate is a nominal
or
an effective rate.
Basically there are three ways to express interest rates, as detailed in Table
4-l.
The right column includes a statement about the effective rate.
For
the first
format, no statement
of
nom
in
al
or
effective is given, but the compounding fre-
quency
is
stated.
The
effective rate must be calculated (discussed in the next
sections). In the second format, the stated rate is identified as effective (or
APY
could also be used), so the rate
is
used directly in computations.
In the third format, no compounding frequency is identified, for
examp
le,
8% per year. Thjs rate is effective only over the time (compounding) period
of
a year, in this case.
The
effective rate for any other time period must
be
calculated.
TABLE
4-1
Various Ways to Express Nominal and Effective Interest Rates
Format
of
Rate
Statement
Nominal rate stated,
compounding period
stated
Effect
iv
e rate stated
Interest rate stated, no
compounding period
stated
Examples
of
Statement
8% per year,
compounded quarterly
Effective 8.243% per year,
compounded quarterly
8% per year
or
2% per quarter
What
about
the
Effective
Rate?
Find effecti ve rate
Use effective rate directly
Rate is effective only
for time period stated;
fi
nd
effec
ti
ve rate for all
other time periods
26
129
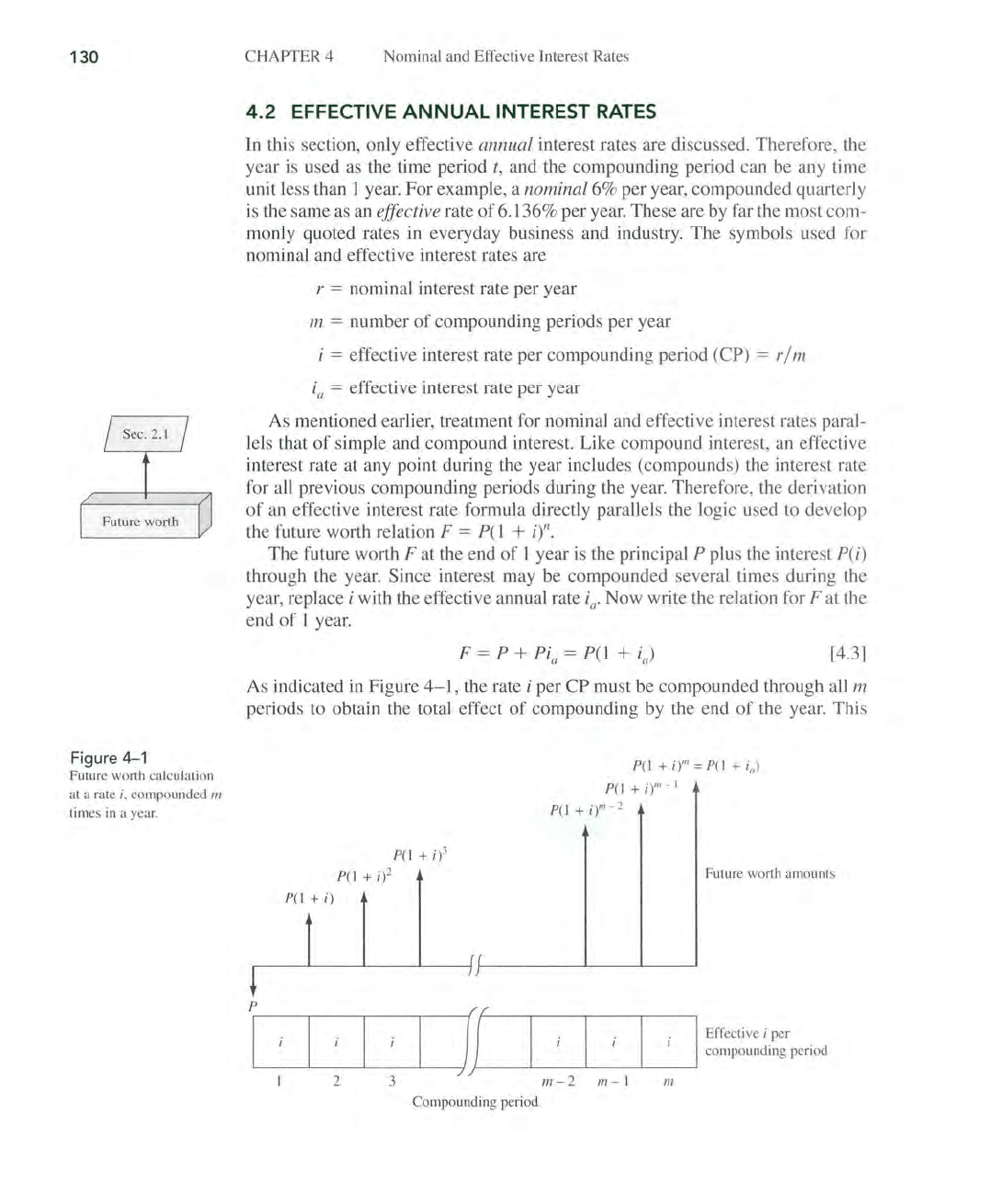
130
Fi
gu
re 4- 1
Future worth
ca
lculation
at
a rate i, compounded
111
tim
es
in a
yea
r.
CHAPTER
4 Nominal and Effective Interest Rates
4.2 EFFECTIVE ANNUAL INTEREST
RATES
In this section, only effective annual interest rates are discussed. Therefore,
th
e
year is used
as
the time period
t,
and the compounding period can be any time
unit less than 1 year.
For
example, a nominal 6% per year, compounded quarterly
is
the same as an effective rate
of
6.136% per year. These are by far the most com-
monly quoted rates
in
everyday business and industry.
The
symbols used for
nominal and effective interest rates are
r = nominal interest rate per year
m = number
of
compounding periods per year
i = effective interest rate per compounding period (CP) = r
im
ia
= effective interest rate per year
As mentioned earlier, treatment for nominal and effective interest rates paral-
lels that
of
simple and compound interest. Like compound interest, an effective
interest rate at any point during the year includes (compounds) the interest rate
for all previous compounding periods during the year. Therefore, the derivation
of
an effective interest rate formula directly parallels the logic used to develop
the future worth relation
F =
pel
+ i)".
The
future worth F at the end
of
1 year is the principal P plus the interest
PO
)
through the year. Since interest may be compounded several times during the
year, replace
i with the effective annual rate i
a
.
Now write the relation for F at the
end
of
1 year.
[4.3]
As indicated in Figure
4-1,
the rate i per
CP
must be compounded through all m
periods to obtain the total effect
of
compounding by the end
of
the year. This
P(I + i)
P
P(I
+ i
)3
P(l
+ i
)2
P(I +
i)
m = P(I + i
,,)
P(I +
i)m
- I
P(l
+ i
)m
- 2
Future worth amounts
I f
'f{
I Effective i per
J
/f----L----'-----"------'
compoundlllg penod
2
3
111-2
1/1
- 1
m
Compounding period

SECTION 4.2 Effective Annual Interest Rates
means that F can also be written as
F =
P(1
+
i)m
[4.4]
Consider the F value for a present worth P
of
$1.
By
equating the two expres-
sions for
F and substituting
$1
for
P,
the effective annual interest rate formula
for
La
is
derived.
1 + ia = (1 +
i)1Il
ia
= (1 +
i)1II
- 1
[4.5]
So Equation [4.5] calculates the effective annual interest rate for any number
of
compounding periods when i is the rate for one compounding period.
If
the effective annual rate
ia
and compounding frequency m are known, Equa-
tion
[4
.
5]
can be solved for i to determine the effective interest rate
per
com-
pounding period.
[4.6]
Further, it
is
possible to determine the nominal annual rate r using the definition
of
i stated above, namely, i = rim.
r%
per
year
=
(i%
per
CP
)(no.
of
CPs
per
year) =
(i)(m)
[4.7]
This is the same as Equation [4.1] where
CP
is the period
of
time.
Jacki obtained a new credit card from a national bank, MBNA, with a stated rate
of
18%
per year, compounded monthly. For a
$1000 balance at the beginning
of
the year, find
the effective annual rate and the total amount owed to MBNA after 1 year, provided no
payments are made during the year.
Solution
There are
12
compounding periods per year. Thus, m =
12
and i =
18%/12
= 1.5% per
month. For a
$1000 balance that
is
not reduced during the year, apply Equation [4.5],
then [4.3] to provide Jacki with the information.
ia
=
(l
+ 0.015)12 - 1 = 1.19562 - 1 = 0.19562
F = $1000(1.19562) = $1195.62
Jacki will pay 19.562%, or $195.62 plus the
$1000 balance, for the use
of
the bank's
money during the year.
Table 4- 2 utilizes the rate
of
18% per year, compounded over different times
(yearly to weekly) to determine the effective annual interest rates over these var-
ious compounding periods. In each case, the compound period rate
L is applied
131

.....
W
N
Compounding
Period
Year
6 months
Quarter
Month
Week
Times
Compounded
per
Year, m
2
4
12
52
I r =
18%
per
year,~~nded
m-Iy I
Rate
per
Compound
Period,
i
18
%
9%
4.5%
l.5%
0.34615%
Distribution
of
i over the Year
of
Compounding Periods
18
%
9%
'_-e
n
9%
2
4.5% 4.5% 4.
5%
4.5%
234
~1
.
5%ineach~
I I I I I I I I I I I I I
L j 4 J b 8 9
10
11
12
~O.34615%ineach~
rffF1[
IIIIII
(Fffn
W,W)
24 26
28
7~
Effective
Annual Rate,
ia
(1.18)'
-1
= 18%
(l.09)2 - 1
= 18.81%
(1.045)4 - 1
=
19
.252%
(l.015)12
-1
= 19.562%
(1.0034615)52 -
I = 19.684%
SECTION 4.2 Effective Annual Interest Rates
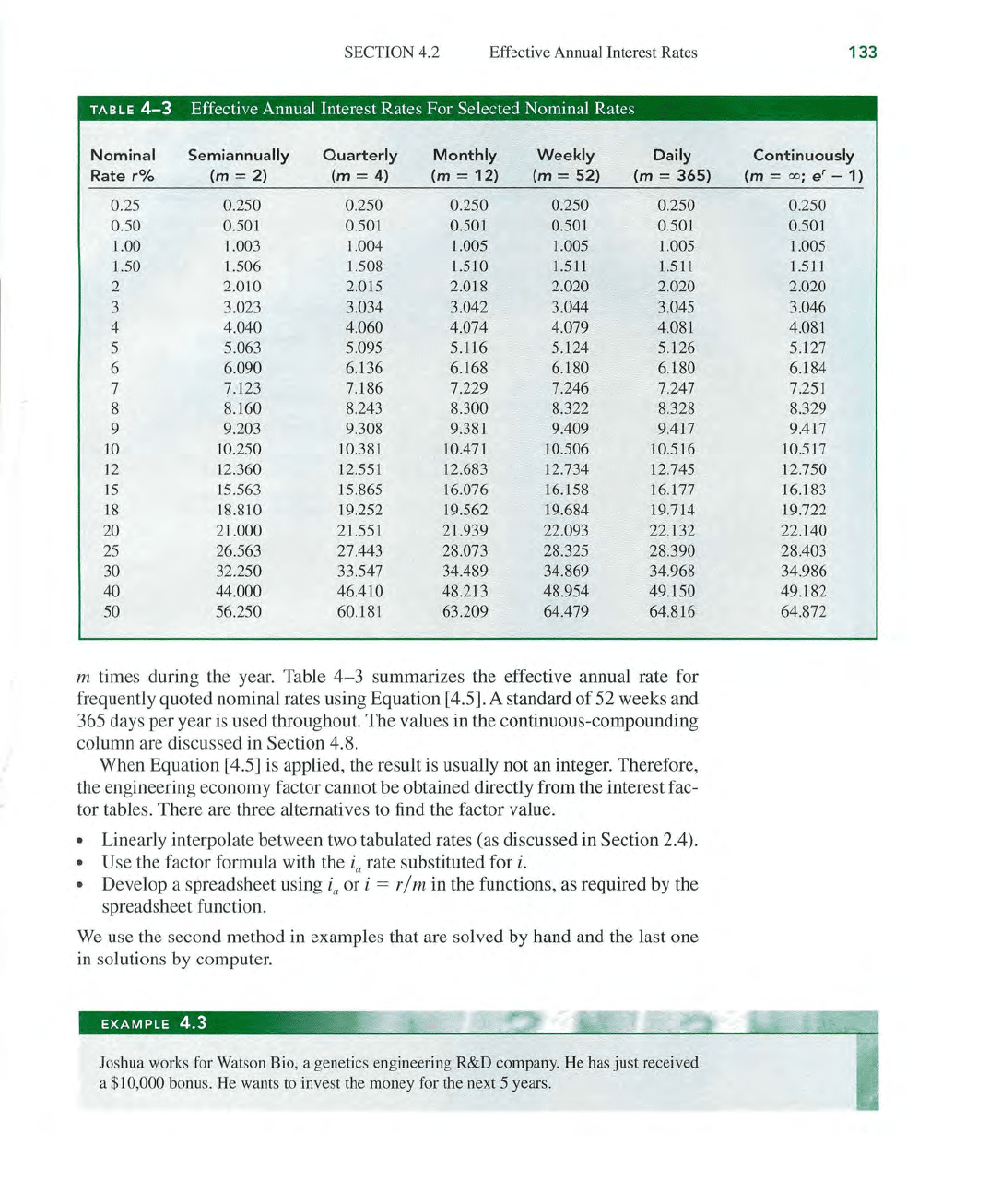
TABLE
4-3
Effective Annual Interest Rates For Selected Nominal Rates
Nominal Semiannually
Quarterly
Monthly
Weekly
Daily
Rate
r%
(m =
2)
(m
=
4)
(m
= 12) (m = 52)
(m
= 365)
0.25 0.250 0.250 0.250 0.250 0.250
0.50 0.501 0.501
0.501
0.501 0.501
1.00
1.003 1.004 1.005
1.005 1.005
1.50 1.506
1.508
1.510
1.5l1
1.5l1
2
2.010 2.015 2.018 2.020 2.020
3 3.023 3.034
3.042 3.044
3.045
4
4.040 4.060
4.074
4.079 4.081
5 5.063 5.095 5.116
5.124
5.126
6
6.090 6.136 6.168 6.180 6.180
7
7.123 7.186
7.229
7.246 7.247
8
8.160
8.243 8.300
8.322 8.328
9 9.203
9.308
9.381
9.409 9.417
10
10.250 10.381 10.471 10.506 10.516
12
12.360 12.551 12.683 12.734 12.745
15
15.563 15.865 16.076 16.158 16.177
18
18.810 19.252 19.562 19.684 19.714
20 21.000 21.551 21.939
22.093 22.132
25
26.563 27.443
28
.073
28.325
28.390
30
32.250
33
.547 34.489 34.869 34.968
40 44.000 46.410
48
.213 48.954 49.150
50 56.250
60.181 63.209 64.479
64.816
m times during the year. Table 4- 3 summarizes the effective annual rate for
frequently quoted nominal rates using Equation [4.5]. A standard
of
52 weeks and
365 days per year
is
used throughout. The values in the continuous-compounding
column are discussed in Section 4.8.
When Equation [4.5] is applied, the result is usually not an integer. Therefore,
the engineering economy factor cannot be obtained directly from the interest fac-
tor tables. There are three alternatives to find the factor value.
• Linearly interpolate between two tabulated rates (as discussed in Section 2.4).
• Use the factor formula with the
ia
rate substituted for
i.
• Develop a spreadsheet using
i"
or
i = r / m in the functions,
as
required by the
spreadsheet function.
We
use the second method in examples that are solved by hand and the last one
in solutions by computer.
Jos
hu
a works for Watson Bio, a genetics engineering R&D company. He has just received
a
$10,000 bonu
s.
He wants to invest the money for the next 5 years.
133
Continuously
(m=oo;e
r
-1)
0.250
0.501
1.005
1.
511
2.020
3.046
4.081
5.127
6.184
7.
251
8.329
9.417
10.517
12.750
16.183
19.722
22.140
28.403
34.986
49.182
64.872

134
'''
oney
Mal
k-e1s
IR
A.
Co
nt
ac
t
Us
Figure
4-2
CHAPTER 4
No
minal and Effective
In
terest Rates
\IB'lA
C
nilicale
01
[)ep\l~lt
Account
Lnjo}
the
,
\d\aJllage~
(lf
a
High
Yield
Certificate
of
Dl'po'it
MBNA
CD yields have consiste
nt
ly
been
am
o
ng
some
of
th
e high
est
n
at
ionwide.
With
a
MBNA
CD
,
yo
u can
sel
ect
the ter
m-
fr
om six
to
60
month
s,
specified in
days or m
ont
h
s-
th
at best s
uit
s
yo
ur
need
s.
MBNA
CD
Accounts
Minimum
Ope
ning Deposit $10,000
Terms C
urr
e
nt
Annual
(month
s)
Int
er
es
t Percentage
Rate Yields (APYs)
6
to
< 9
1.74%
1.75%
9 to
< 12 1.89% 1
.9
0%
12
to
<
18
2.38% 2
.4
0%
18
to < 24
2.
72%
2.7
5%
24
to < 30 2.86% 2.90%
30
to < 36
3.20%
3.25%
36
to
< 48 3.40% 3.45%
48
to
<
60
3.83% 3.90%
60
4.
36
% 4.45%
*CD APYs for
th
e te
rm
s sh
ow
n above are val
id
for
th
e period
fr
om 06/0
7/
04 to 06
/1
3/
04 and assume
interest remains in
th
e account until maturity.
Minimum opening balan
ce
is $10,
000
for a
ll
te
rm
s
shown ab
ove
. Withdrawals and fees may reduce
ea
rn
in
gs on
th
e account. A penalty may be
imposed for ea
rl
y withdrawal
of
CD
principal.
Certifica
te
of
Dcpo<;i! Account,>
3.
45%*APY
3&-month
Term
It! Inlmum Opening Balance $10.000
Open
an
acc
ount
:
Submit an Online
New
Account
Form
(;,,11
MBNA
at 1-800-900-6693
(mantion code HA
04U
)
TTY users,
ca!l1·
800· 21
5-4549
Collact calls, dlal
(3
02) 457
-0
719
Internet ad showing interest rates on
Ce
rtificates of
Dep
osi
r.
Th
e ad de
pi
cted is a sample, similar to
one
that appeared on
June
11,
20
04, on the MBNA Ame
ri
ca Ba
nk
website www.mbna.
co
m. The rales shown are not current.
Jos
hu
a saw an MBNA America bank website ad for Certificate
of
Deposit (CD) interest
rates (Figure
4-
2).
He
is
thinking
of
putting the $10,000 into a
CD
for 5 years for capital
prese
rv
a
ti
on. Alte
rn
atively, he is thinking
of
investing it all for the next 2
yea
rs
in
stock
s,
where he estimates he can make an effective annual rate
of
10%. Once he has made this
lar
ge
r up-front return, he will then be more conservative and place the entire amount in a
CD for
th
e
final
3 year
s.
Help Joshua
wid1
the following:
(a) Determine the compounding period for the 3- and 5-year CDs, since
th
ey a
re
not
included in
th
e website ad.
Get
as close as possible
to
the quoted APY rounded to
two dec
im
als.
(b) Determine
th
e total amount be w
ill
have
af
ter 5 years for the two options he has
outlined.
