Blank L., Tarquin A. Engineering Economy (McGraw-Hill Series in Industrial Engineering and Management)

SECTION 2.5 Arithmetic Gradient Factors (P

IG

and AI

G)

Since the va

lu

e

of

th

e factor decreases as n increases, c is subtracted from the factor

va

lu

e for

It

= 45.

x = 0.17l2 - 0.0183 = 0.1529

Comment

Though

it

is

possible to perfo

rm

two-way linear interpolation,

it

is much easier and

more accurate to use

th

e factor form

ul

a or a spreadsheet function.

2.5 ARITHMETIC GRADIENT

FACTORS

(PIG

AND

AIG)

An arithmetic gradie

nt

is a cash flow series that either increases or decreases by

a

co

nstant amount.

The

cash flow, whether income

or

disbursement, changes by

th

e same arithmetic amount each period.

The

amount

of

the increase

or

decrease

is the gradie

nt.

For

examp

le, if a manufacturering engineer

pr

edicts that the cost

of

maintaining a robot will increase by

$500

per year until the machine is retired,

a gradient series is involved and the amount

of

the gradient is

$500

.

Form

ul

as

pr

eviously developed for an A series have year-end amounts

of

equal

valu

e.

In

th

e case

of

a gradient, each year-end cash flow is different, so new for-

mulas

mu

st be derived. First, assume that the cash

fl

ow at the end

of

year I is not

part

of

th

e gradient series, but is rather a base amount. This is convenient because

in

ac

tu

al applications, the base amount is usually larger

or

smaller than the gra-

dient increase or decrease.

For

example,

if

you purchase a used

car

with a

I-year

warranty, you might expect to pay the gasoline and insurance costs during the first

year

of

operation. Assume these cost $1500; that is, $1500 is the base amount.

After

th

e

fi

rst year, you absorb the cost

of

repairs, which could reasonably be

expected to increase each year. If you estimate that total costs will increase by

$50 each year, the a

mount

the second year is $1550, the third $1600, and so on to

year

n,

when the total cost is 1500 + (n - 1)50.

The

cash

fl

ow diagram is shown

in

Figure

2-10.

Note

that the gradient ($

50

) is first observed bet

wee

n year 1 and

year 2, a

nd

the base amount ($ 1500 in year

1)

is not equal to the gradient.

Define the sy

mb

ol G for gradients as

G = constant arithmetic change in the magnitude

of

receipts

or

disburse-

ments from one time period to the next; G may be positive or negative.

o

2

3

$ 1500

$ 1550

$ 1600

4

J

$1650

/'I - I

/'I

$ 1500

+

(11

- 2)

50

$1500

+

(11-

1

)5

0

65

Figure 2-

10

Diagram of an arithme

ti

c

gradient se

ri

es wi

th

a

base amount

of

$ 1500

an

d a gradient

of

$

50

.

66

Figure 2-11

Conventional arithmetic

gradient se

ri

es without

th

e

ba

se amount.

CHAPTER 2 Factors: How Time and Interest Affect Money

4G

(n -

2)G

(n - J)G

The cash flow

in

year n

(CF

Il

) may be calculated

as

CF

Il

= base amount + (n -

l)G

If

the base amount is ignored, a generalized arithmetic (increasing) gradient cash

flow diagram is

as

shown in Figure 2-11. Note that the gradient begins between

years 1 and

2.

This

is

called a conventional gradient.

EXAMPLE

2.9

;~~

.

A sports apparel company has initiated a logo-licensing program. It expects to realize a

revenue

of

$80,000

in

fees next year from the sale

of

its logo. Fees are expected

to

in-

crease uniformly to a level

of

$200,000 in 9 years. Determine the arithmetic gradient

and construct the cash

flow

diagram.

Solution

The base amount

is

$80,000 and the total revenue increase

is

Increase in 9 years = 200,000 - 80,000 = 120,000

G d

·

increase

ra

lent =

---

n - 1

120,000

=

~

= $15,000 per year

The cash

flow

diagram is shown in Figure 2-12.

G = $15,000

$140,000

$125,000

$110,000

$95,000

$80,000

o 2 3 4 5

Figure

2-12

Diagram for gradient series, Example 2.9.

$185,000

$170,000

$155,000

6 7 8

$200,000

9

Year

SECTION 2.5 Arithmetic Gradient Factors

(PIG

and

AI

G)

In this text, three factors are derived for arithmetic gradients: the

PIG

factor

for present worth, the

AI

G factor for annual series and the

FIG

factor for future

worth. There are several ways to derive them. We use the single-payment present

worth factor

(PI

F,i,n), but the same result can be obtained using the F I P, F I

A,

or

PIA

factor.

In Figure

2-11, the present worth at year 0

of

only the gradient is equal to the

sum

of

the present worths

of

the individual values, where each value is consid-

ered a future amount.

P = G(PIF,i,2) + 2G(PIF,i,3) + 3G(PIF,i,4) +

...

+

[(n

-

2)G](PIF

,i,n

-1)

+

[(n

-l)G](PIF,i,n)

Factor out G and use the

PI

F formula.

P = G + + +

...

+ +

[211]

l

1 2 3

n-2

n-1J

(1

+

if

(1

+

i)3

(1

+

i)4

(1

+

on

- I

(1

+ i)" .

Multiplying both sides

of

Equation [2.11] by

(1

+ 0

1

yields

l

1 2 3

n-2

n-1

J

P(l

+ i) 1 = G

(1

+

i)1

+

(1

+

if

+

(1

+

i)3

+

...

+

(1

+

on

-2 +

(1

+

on

- I

[2.12]

Subtract Equation [2.11] from Equation [2.12] and simplify.

iP =

Gl

1 + 1 +

...

+ 1 + 1 J -

Gl--n-J

(1

+

i)1

(l

+

if

(1

+

i)n-l

(1

+ i)"

(1

+ i)"

[2.13]

The left bracketed expression is the same as that contained in Equation [2.4],

where the

PIA

factor was deri ved. Substitute the closed-end form

of

the

PIA

fac-

tor from Equation [2.6] into Equation [2.13] and solve for

P to obtain a simpli-

fied relation.

G

l(1

+ i)" - 1 n J

P - i i(1 +

i)"

- (1 +

i)"

[2.14]

Equation

[2.14]

is

the general relation to convert an arithmetic gradient G (not in-

cluding the base amount) for n years into a present worth at year

O.

Figure

2-13a

is

converted into the equivalent cash flow

in

Figure

2-13b

.

The

arithmetic-gradient

present worthfactor, or

PIG

factor, may be expressed in two forms:

. 1

l(1

+

it

- 1 n J

(PIG,l,n) = i

i(l

+ i)" -

(1

+

i)"

(1

+

it

- in - 1

(PIG,i,n) =

i2(1

+ i)"

or

[2.15]

Remember:

The

gradient starts in year 2 and P is located in year

O.

Equation

[2.14] expressed as an engineering economy relation is

P = G(PIG,i,n)

[2.16]

67

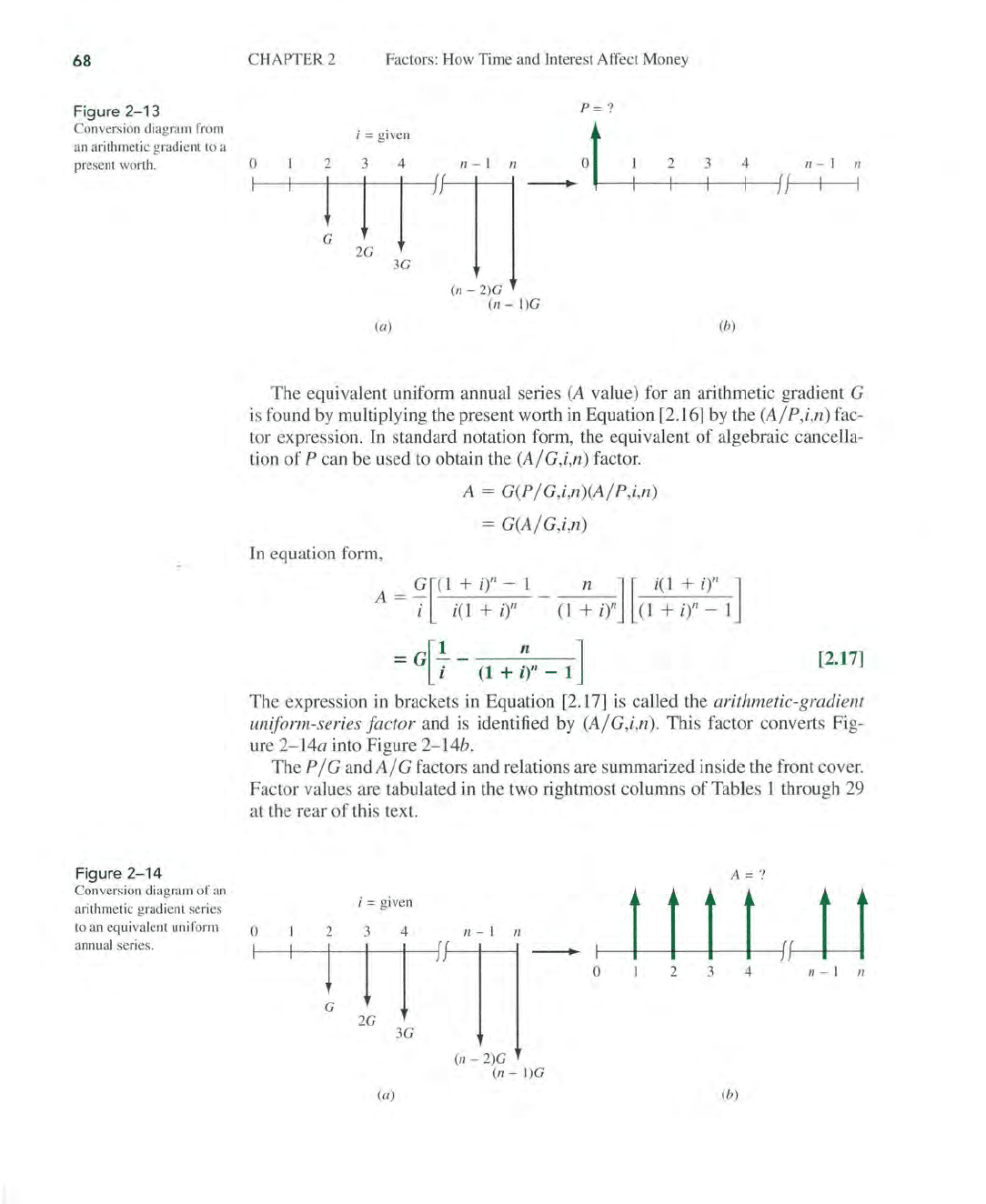
68

Figure

2-13

Conversion diagram from

an

arithm

et

ic gr

ad

ient to a

pre

se

nt worth.

Figure

2-14

Conversion diagram of

an

arithmetic gradient

ser

i

es

to

an

e

quiv

alent

unif

or

m

annual

se

ri

es.

CHAPTER 2

Factors: How Time a

nd

Interest Affect Money

p=

?

i = gi

ve

n t

0f---+_

-+

2

__

3

t----j4_---if

f-n_

-

+-I--jn

_ 0

.-

_-+-_+2

_--1

3

1---+

4

_-1f

fr--

'-' -

;-1

---j"

II!

I I I I

3G

(n - 2)G

(n

- I)G

(a)

(b)

The

equIvalent uniform annual series

(A

value) for an arithmetic gradient G

is found by multiplying the present worth in Equation [2.16]

by

the

(AI

P,i,n) fac-

tor expression. In standard notation form, the equivalent

of

algebraic cancella-

tion

of

P can be used to obtain the (AIG,i,n) factor.

A

=

G(PIG,i,n)(AIP

,i,n)

= G(AIG,i,n)

In equation form,

G[(1 +

it

- 1

n]

[ i(1 + i)" ]

A = i i(1 +

it

-

(1

+

it

(1

+ i)" - I

-

G[

~

-

(1

+

Zn

- 1 ]

[2.17]

The

expression

in

brackets in Equation [2.17]

is

called the arithmetic-gradient

uniform-series

fa

ctor and is identified by (AIG,i,n). This factor converts Fig-

ure

2-14a

into Figure 2

-14b

.

The

PIG and A I G factors and relations are summarized inside the front cover.

Factor values are tabulated in the two rightmost columns

of

Tables 1 through 29

at the rear

of

this text.

°

I

2

l

G

i = given

3

4

I

J

2G

3G

(a)

A = ?

n - I

It

-

t t t t r

lJ

0

2 3 4

n - I

11

(n - 2)G

(n - I)G

(b)

SECTION 2.5 Arithmetic Gradient Factors

(PIG

and

AI

G)

There

is

no direct, single-cell spreadsheet function

to

calculate P or A for

an

arithmetic gradient. Use the NPV function for

P,

and the PMT function for A,

after all cash flows are entered into cells. (The use

ofNPV

and PMT functions for

this type

of

cash flow series is illustrated in Chapter 3.)

An F

/G

factor (arithmetic-gradient future worth factor) can be derived by

multiplying the

PIG

and

F/P

factors. The resulting factor,

(F/G,i,n),

in

brack-

ets, and engineering economy relation is

The total present worth

P T for a gradient series must consider the base and the

gradient separately. Thus, for cash flow series involving conventional gradients:

• The base amount is the uniform-series amount A that begins in year 1 and

extends through year

n. Its present worth is represented by P

A

.

• For an increasing gradient, the gradient amount must be added to the uniform-

series amount. The present worth

is

Pc.

•

For a decreasing gradient, the gradient amount must be subtracted from the

uniform-series amount. The present worth is

- Pc.

The general equations for calculating total present worth P T

of

conventional

arithmetic gradients are

and

[2.18]

Similarly, the equivalent total annual series are

AT =

AA

+

Ac

and AT =

AA

-

AG

[2.19]

where

AA

is the annual base amount and

Ac

is the equivalent annual amount

of

the gradient series.

A-I"::.

'>Z~oc.?o

-+-

rJO,ouo

Three contiguous counties

in

Florida have agreed

to

pool tax resources already desig-

nated for county-maintained bridge refurbishment. At a recent meeting, the county

engineers estimated that a total

of

$500,000 will be deposited at the end

of

next year

into

an

account for the repair

of

old and safety-questionable bridges throughout the

three-county area. Further, they estimate that the deposits will increase

by

$100,000 per

year for only 9 years thereafter, then cease. Detennine the equivalent

(a) present worth

and

(b) annual series amounts if county funds earn interest at a rate

of

5% per year.

Solution

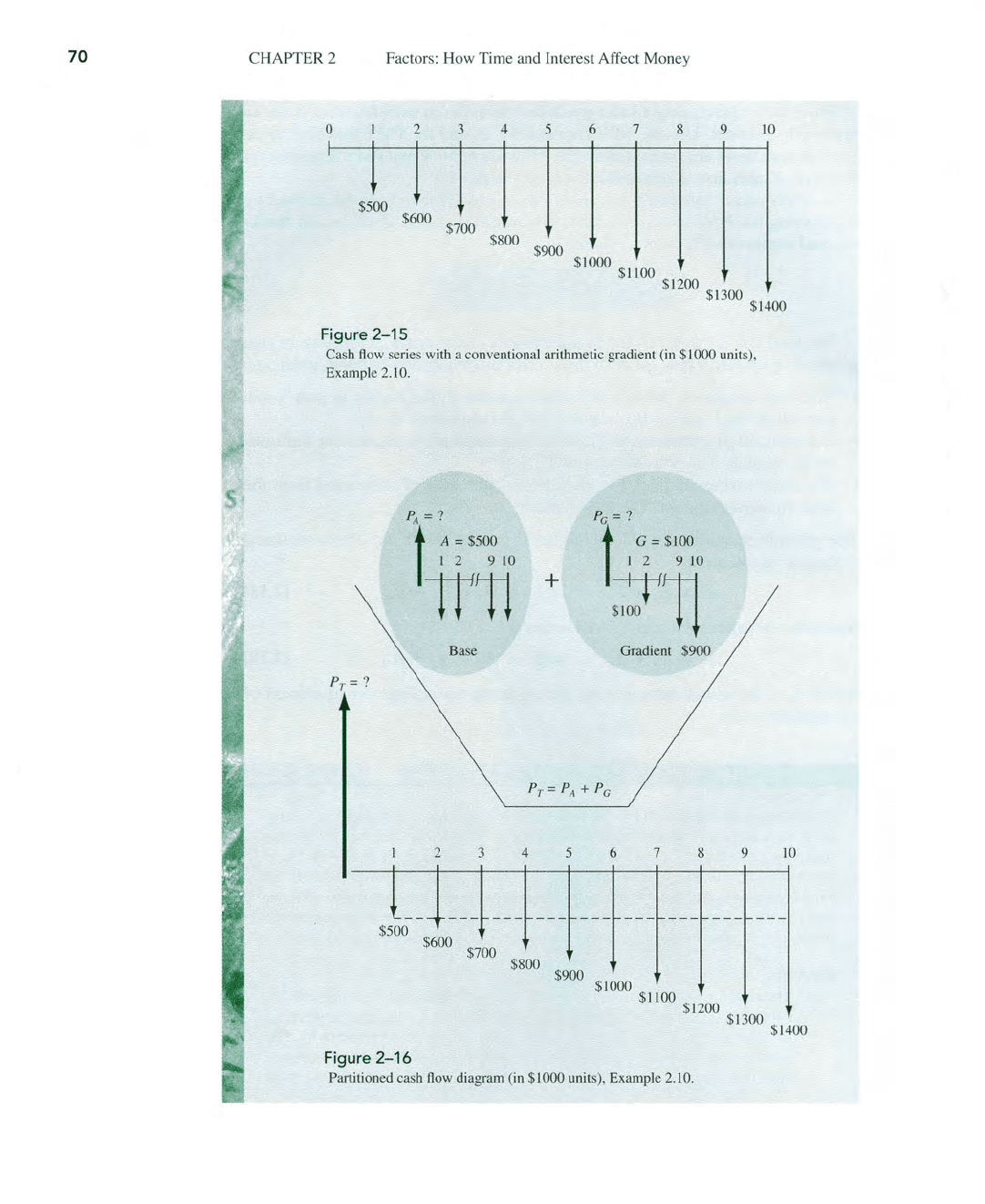
(a) The cash flow diagram from the county's perspective is shown in Figure 2-15.

Two computations must be made and added: the first for the present worth

of

the base amount P

A

and a second for the present worth

of

the gradient Po. The

total present worth

P

T

occurs in year

0.

This

is

illustrated

by

the partitioned

cash

flow

diagram

in

Figure 2-16. In $1000 units, the present worth, from

69

~

1\

Q-Solv

70

CHAPTER 2 Factors: How Time and Interest Affect Money

o

2

3

4

5

6 7 8 9 10

$500

$600 $700

$800 $900

$1000

$1100

$1200

$1300

$1400

Figure

2-15

Cash

fl

ow series with a conventional arithm

et

ic gradient (in $

10

00 units),

Example 2

.1

O.

P

T

= ?

P

A

= ?

$500

t

A = $500

1 2

910

1r11

Base

2 3 4

$600 $700

$800

+

5

$900

Pc = ?

t

G=

$

LOO

I 2 9

JO

::r11

Gradient $900

6

7

8 9

$

10

00

$

]]

00

10

$1200

$1300 $ 1400

Figure

2-16

Partitioned cash flow diagram

(i

n $1000 units), Example

2.

10.

SECTION 2.6 Geometric Gradient Series Factors

Equation [2.18],

is

P

T

= 500(P/A,5%,

IO)

+ 100(P/G,5%,10)

= 500(7.7217) + 100(31.652)

= $7026.05 ($7,026,050)

(b) Here, too,

it

is necessary to consider the gradient and the base amount separately.

The total annual series

kr

is

found by using Equation [2.19].

AT

= 500 + 100(A/G,5%,1O) = 500 + 100(4.0991)

= $909.91 per year ($909,910)

And

AT

occurs from year 1 through year 10.

Comment

Remember: The P

/G

and

A/G

factors determine the present worth and annual series

of the

gradient only. Any other cash

flow

must be considered separately.

If

the present worth

is

already calculated [as

in

part

(a)],

P T can be multiplied

by

the

appropriate

A/

P factor to get

AT'

AT

= P

T

(A/P,5%,1O) = 7026.05(0.12950)

= $909.87 ($909,870)

Round-otf accounts for the $40 difference.

Additional Example 2.16.

2.6 GEOMETRIC GRADIENT

SERIES

FACTORS

It

is common for cash flow series, such as operating costs, construction costs, and

revenues, to increase or decrease from period to period by a

constant percentage,

for example, 5% per year. This uniform rate

of

change defines a geometric gra-

dient series

of

cash flows.

In

addition to the symbols i and n used thus far, we

now need the term

g

= constant rate

of

change, in decimal form, by which amounts

increase or decrease from one period to the next

Figure

2-17

presents cash flow diagrams for geometric gradient series with in-

creasing and decreasing uniform rates. The series starts in year 1 at an initial

amount

A

I'

which is

not

considered a base amount as in the arithmetic gradient.

The relation to determine the total present worth

~

for

the entire

cashfiow

series

may be derived by multiplying each cash flow in Figure

2-17

a by the P / F factor

I/O

+i)l1.

AI AI

(l

+

g)

AI

(l

+

g)2

Aj(1

+

gt

-

I

P = + + + . . . + -""-'----"'-'---

~

(1

+

i)1

0+i)2

(1+i)

3

(1+it

= A

--

+ + + .

..

+ - ----''---

l

1 L + g

(1

+

g)2

(1

+

gY

-

I

]

I 1 + i

(1

+

i)2

(1

+

i?

(1

+ i)"

[2.20]

71

72

o

AI

Figure 2-17

CHAP

TE

R 2

Factors: How T

im

e a

nd

Interest Affect Money

i = given

g = given

2

3

4 n 0

AI(I + g)

......

AI(I +

gP

.....

A

ie

l + d ))(

"-

AI

(l

+g),,

- I

(a)

'/

AI

i = given

g = given

2

3

4

n

J:-J

_ -

-J

f-A

-( 1 _ g

)"

- I

-A

I

(l

-g

)3 I

/A

1

(1

-g?

//A

I( l

-g)

(b)

Cash now

di

agram of (a)

in

creas

in

g and (b) d

ec

reas

in

g

geo

metric gra

di

ent se

ri

es and present worth P

g

.

Multiply both sides by

(1

+

g)/(1

+

i)

, subtract Equation [2.20] from

th

e result,

factor out P

g

,

and obtain

P

--

- 1 - A

---

(

1

+ g ) [

(1

+ gY

1]

g 1 + i - . I

(1

+ i)n+ I 1 + i

Solve for P

g

a

nd

simplify. [ 1 + g)

ll

]

P

g

=

AI

1 -

.1+i

l

-g

g

*-

i

[2.

21

]

The term

in

brackets in Equation [2.21] is the geometric-gradient-series present

worth factor for values

of

g not equal to

th

e interest rate

i.

The standard notation

us

ed is (P / A,g,i,n). When g = i, substitute i for g in Equation

[2.

2

0]

to obtain

P

=A(

_ 1_ + _ 1

_+_

1_ +

..

.

+_

1_ )

g

1(1+i

)

(l

+

i)

(l

+ i)

(l+

i)

The term 1/

(1

+ i) appears n time

s,

so

nA I

P =

--

g

(1

+ i)

[2.22]

In summary,

th

e engineering economy relation and factor formulas to calculate

P

g

in

period t = 0 for a geometric gradient series starting in period 1 in

th

e

amount A I and increasing by a constant rate

of

g each period are

P

g

= A

1

(P/

A,g,i,n)

1 _

(1

+ g

11

1 + i

(P/

A,g,i,n)

= i - g

n

1 + i

[2.23]

[2.24]

g = i

SECTION 2.6 Geometric Gradient Series Factors

It is possible

to

derive factors for the equivalent A and F values; however, it

is

easier

to

determine the P

g

amount and then multiply

by

the

AlP

or F I P factor.

As

with the arithmetic gradient series, there are no direct spreadsheet func-

tions for geometric gradients series.

Once the cash flows are entered, P and A

are determined

by

using the NPV and PMT functions, respectively. However, it

is always an option

to

develop on the spreadsheet a function that uses the fac-

tor equation

to

determine a

P,

F, or A value. Example

2.11

demonstrates this

approach

to

find the present worth

of

a geometric gradient series using Equa-

tions [2.24].

EXAM

PLE

2.11

:~;

Engineers at Sea World, a division

of

Busch Gardens, Inc., have completed an innovation on

an

existing water sports ride to make

it

more exciting. The modification costs only $8000

and is expected to last 6 years with a $1300 salvage value for the solenoid mechanisms. The

maintenance cost

is

expected

to

be high at $1700 the first year, increasing

by

II

% per year

thereafter. Determine the equivalent present worth

of

the modification and maintenance cost

by

hand and

by

computer. The interest rate is 8% per year.

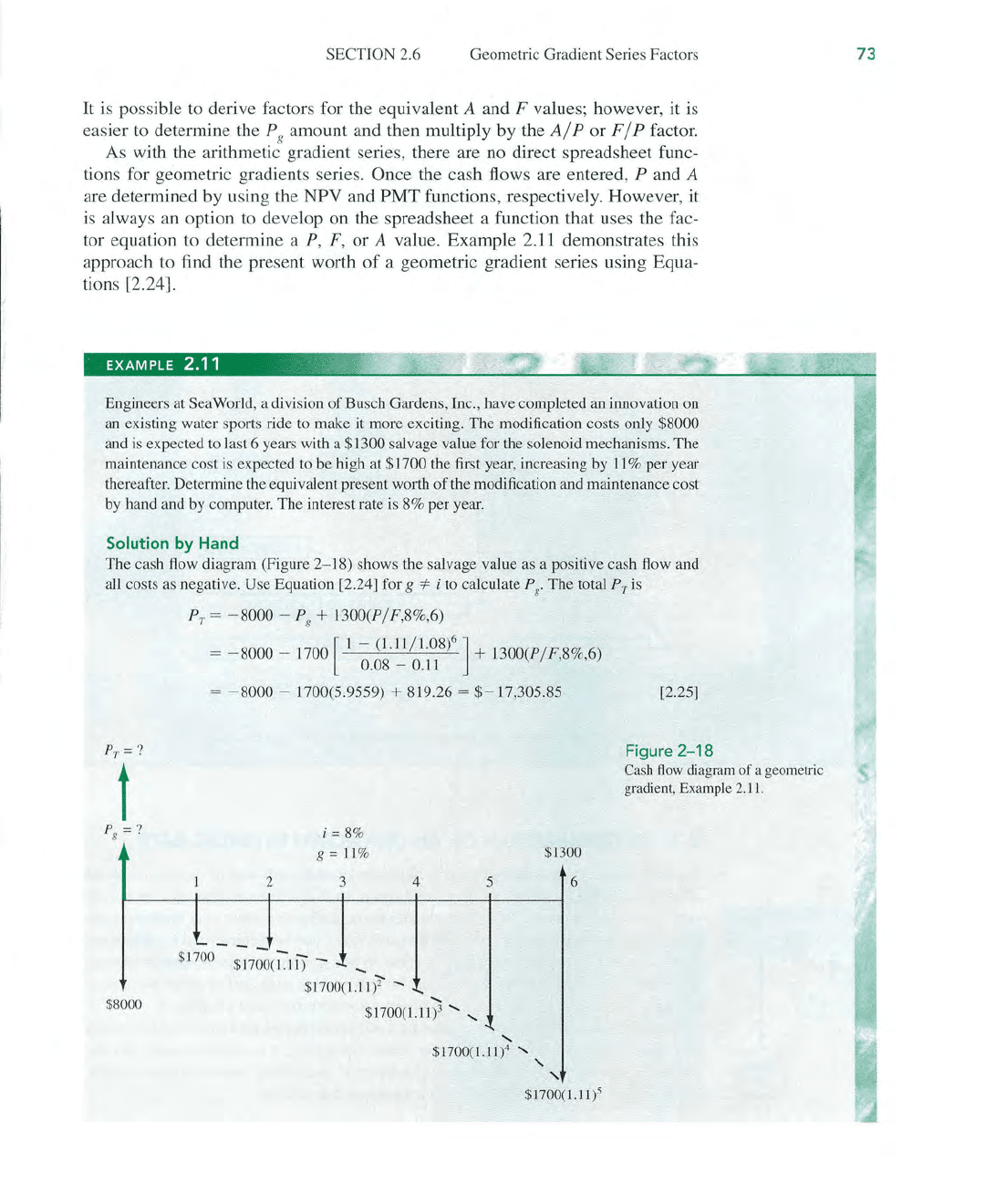
Solution

by

Hand

The cash flow diagram (Figure 2- 18) shows the salvage value

as

a positive cash flow and

all costs

as

negative. Use Equation [2.24] for g

*-

i to calculate P

g

.

The total PI' is

?T=

?

t

p

=?

g .

$8000

PI'

= - 8000 - P

g

+

1300(P/F,8%,6)

= - 8000 - 1700 [ 1 - (1.1

1/1.08)6]

+

1300(P/F

8% 6)

0.08 -

0.11

. "

= - 8000 - 1700(5.9559) + 819.26 =

$-17,305.85

2

i=8%

g = 11%

3

4

l

__

$1700 $17;;;(

1:"1

i)

-

$l700(1.l1l

......

.....

$1700(1.11)3

..........

5

"-

$1300

6

$1700(1.l1)4 "-

,

$1700(1.11)5

[2.25]

Figure

2-18

Cash flow diagram

of

a geometric

gradient, Example 2.11.

73

74

m

E·Solve

CHAPTER 2 Factors: How Time and Interest Affect Money

Solution by

Computer

Figure

2-19

presents a spreadsheet with the total present worth

in

cell B

13.

The function

used to determine

P

T

=

$-17,305.89

is

detailed

in

the cell tag.

It

is

a rewrite

of

Equation

[2.25].

Since

it

is

complex, column C and 0 cells also contain the three elements

of

P

T

,

which are summed

in

013

to obtain the same result.

X M,cro.oft

Excel·

Example

211

I!lIiII3

Cate 0

Estimates

PWv

a

lue

s

First cost

·$8,000

Ex

pected life. n years

8 Salvage

va

lu

e

·$8,000

6

$1,300

.$1 ,700

$819.22

--l

=PV(BI

I,B7,0

,-

B8) I

5.95595 ·10125.

11

9 Mai ntenan

ce

cost

(1

st year)

Maint cost

gradie

nt

, g% per year

In

terest

ra

te, % per year

11%

8%

12

13

Total prese

nt

wo

rth

14

.$

17,305.89

~

=

SUM(D6:DI2)

1

.$

17,305.89

15

~

= (( 1

-((

1 + B 10)/(1 + B

II))"B7)/

(B

11

- B 10))

181

= B6+ B9*(( 1

-((

1+ B

10

)l(

1+ B

11

))"B7)/(B

11

- B 10))+

PV(BII

,B7,0

,-

B8)

19

l.i

••

I\

E"ample2.ll

~

'

I

Read'

NUM

Figure

2-19

Spreadsheet used to determine present wOlth

of

a geometric gradient with g =

II

%, Example 2.

11

.

2.7 DETERMINATION OF

AN

UNKNOWN

INTEREST

RATE

In some cases, the amount

of

money deposited and the amount

of

money received

after a specified number

of

years are known, and it is the interest rate

or

rate

of

return that

is

unknown. When single amounts, uniform series,

or

a uniform con-

ventional gradient is involved, the unknown rate

i can be determined by direct so-

lution

of

the time value

of

money equation. When nonuniform payments

or

several

factors are involved, the problem must be solved by a trial-and-error

or

numerical

method.

These

Blank L., Tarquin A. Engineering Economy (McGraw-Hill Series in Industrial Engineering and Management)

Подождите немного. Документ загружается.