Blank L., Tarquin A. Engineering Economy (McGraw-Hill Series in Industrial Engineering and Management)
Подождите немного. Документ загружается.


SECTION 2. 1 Single-Payment Factors (F / P a
nd
P / F)
Use the P/F factor
to
determine P three years earlier.
P = F(P / F,i,n) = $50,000(P / F,20%,3)
= 50,000(0.5787) = $28,935.00
An
equivalence statement
is
that $28,935 three years ago is the same as $50,000
today, which will grow
to
$124,415 five years from now, provided a 20% per year
compound interest rate is realized each year.
Use
th
e PY function
PV(i
%,
/1
,A,F) and omit the A value. Figure
2-2a
shows the result
of
ent
er
in
g PV(20%,3,,50000)
in
ce
ll
F4 to be the same as using the P / F factor.
Solution by
Computer
(c) Figure
2-2b
is a complete spreadsheet solution on one worksheet with the chart.
Two columns are used for 20% and 5% computations primarily so the graph can be
developed
to
compare the F and P values. Row
14
shows the F values using the FY
function with the format FY(i%,5,0,
- 50000) where the i values are taken from cells
C5 and
05.
The future worth F = $124,416
in
cell C14
is
the same (round-off
considered)
as
that calculated above. The minus sign on 50,000 makes the result a
po
siti
ve
number for the chart.
The PY function
is
used
to
find
the P values
in
row
6.
For example,
th
e present
worth at
20%
in
year
-3
is
determined
in
cell C6 using the PY function. The
re
sult
P = $28,935 is
dl
e same as
th
at obtained by using the P / F factor previously. The
chart graphica
ll
y shows the noticeable difference that 20% versus 5% makes over
the 8-year span.
EXAMPLE
2.3
.il
An
independent engineering consultant reviewed records and found tbat the cost
of
office supplies varied
as
shown
in
the pie chart
of
Figure
2-3.
If the engineer wants to
know the equivalent value
in
year
10
of
only the three largest amounts, what
is
it at
an
interest rate
of
5% per year?
YrO
Yr
4
---L-----~
Y:-r-::5
Figure
2-3
Pie chart
of
cos
ts
, Example 2.3.
55
Q-
So
lv
~
E-Solve

56
CHAPTER 2 Factors: How Time a
nd
Interest Affect Money
F=
?
i=5
%
o 2 3
4
5 6 7 8 9
10
$300
$400
$
600
Fi
gure
2-4
Diagram for a future worth
in
year
10,
Example 2.3.
Solution
Draw the cash flow diagram for the values $600, $300, and $400 from the engineer's
perspective (Figure
2-4).
Use F I P factors
to
find F
in
year 10.
F =
600(F
I P,5%, 10) + 3DO(F I P,5%,8) +
400(F
I P,5%,5)
= 600( 1.6289) + 300(1.4775) + 400(1.2763)
= $1931.11
The problem could also be solved by finding the present worth in year
0
of
the $300
and $400 cos
ts
using the PI F factors and then finding the future worth
of
the total
in
year I
O.
Comment
P = 600 +
300(P
I F,5%,2) +
400(P
I F,5%,5)
= 600 + 300(0.9070) + 400(0.7835)
= $1185.50
F =
1185.50(FIP,5%,l0)
= 1185.50(1.6289)
= $1931.06
It should be obvious that there are a number
of
ways the problem could be worked,
since any year could be used
to
find the equivalent total
of
the costs before finding the
future value
in
year 10. As an exercise, work the problem using year 5 for the equiva-
lent total and then determine the final amount in year 10. All answers should be the
same except for round-off error.
2.2 UNIFORM-SERIES PRESENT WORTH FACTOR
AND
CAPITAL RECOVERY FACTOR
(P
IA
AND
Al
P)
The equivalent present worth P
of
a uniform series A
of
end-of-period cash flows
is shown in Figure
2-5a.
An
expression for the present worth can be determined
by considering each
A value as a future worth F, calculating its present worth

SECTION 2.2 Uniform-Series Present Worth Factor and Capital Recovery Factor
57
p=
? P = given
i = given
i = g
iv
en
o
2
/1
- 2
/I
- I IZ o
2
/1
- 2
/I
- I IZ
~TTl
A = g
iv
en
(a)
Figure
2-5
Cash
/l
ow
di
agrams used to determine (a) P
of
a uniform series and (b) A for a present worth.
with the P / F factor, and summing the results.
The
equation is
A = ?
(b)
The
terms
in
brackets are the P / F factors for years I through n, respectively.
Factor
out
A.
P = A + + + .
..
+ +
---
[
I 1 1 1
I]
(1
+
i)1
(1
+ i)2
(1
+ i)3
(l
+ i)"- I
(1
+
it
[2.4]
To simplify Equation [2.4] and obtain the
P / A factor, multiply the
n-term
geo-
metric progression
in
brackets by the (P / F, i%, 1) factor, which is
1/(1
+ i). This
results
in
Equation
[2.S]
below. Then subtract the two equations, [2.4] from
[2
.
S],
and simplify to obtain the expression for P when i
-=1=
0 (Equation [2.6]). This
progression follows.
~
=
A[
1 + 1 + 1 +
...
+ I + 1 ]
1 + i
(1
+ i)2
(l
+ i)3
(1
+
i)4
(1
+ i)"
(1
+ i)"+ I
_l_
P=A[
_
--"<-::-
1 + i
(1
+ i
-P=
A[
1 +
~_
-=-
(l+i)
1 (
~P=A[
1 _
1 + i
(1
+
0"
+ 1
(l
~
i)1
]
A
[1
]
p - -
-1
- i
(I
+ i)"
(1
+
i)"
- 1
P
= A [
i(l
+ i)" ]
i
#=
0
[2.S]
(1
+1
i)" + I ]
~
it
]
[2.6]

58
CHAPTER 2 Factors: How Time and Interest Affect Money
The
term in brackets in
Equation
[2.
6]
is
the conversion factor referred to as the
uni;form-series present worth Jactor
(USPWF).
It is the
PIA
factor used to cal-
culate the
equivalent P value in
year
0 for a uniform end-of-period series
of
A
valu
es
beginning at the
end
of
period 1
and
extending
for
n periods.
The
cash
flow
diagram
is
Figure
2-5a
.
To reverse the situation, the present worth P is
known
and the equivalent
uniform-series
amount
A is
sought
(Figure 2- 5b).
The
first A value occurs at the
end
of
period 1, that is,
one
period
after P occurs.
Solve
Equation [2.6] for A to
obtain
i(l
+ i)"
A =
p[
(1
+
i)"
- 1 ]
[2.7]
The term in brackets
is
called the capital recovery Jac
tor
(CRF),
or
AI P Jactol:
It
calculates the equivalent uniform annual worth A
over
n years
for
a given P in
year
0, when the interest rate is i.
These formulas
are
derived with the present worth P
and
the first uni-
form annual
amount
A one year (period) apart.
That
is, the
present
worth
P
must
always be located one period
prior
to the first A.
The
factors and their use to find P
and
A are
summarized
in Table
2-2,
and
inside
the front cover.
The
standard notations for these two factors
are
(pi
A,i
%,n) and
(AI
P,i%,n). Tables 1 through 29 at the end
of
the text inclu
de
the factor values.
As an example,
if
i = 15% and n = 25 years, the
PIA
factor value from Table 19
is
(PIA,15%
,25) = 6.4641.
This
will find the
equivalent
present worth
at
15
%
per
year
for any
amount
A that occurs uniformly from years 1 through 25.
When
the bracketed relation in Equation [2.6] is used to calculate the pi A factor, the re-
sult
is
the
same
except
for
round-off
errors.
(1
+
0"
- 1 (1.15)25 - 1 31.91895
646
(
PIA
15% 25) = = = = . 415
" i(1 +
it
0.15(1.15f5
4.
93784
Spreadsheet
functions are
capable
of
determining both P and A values
in
lieu
of
applying the
PIA
and Al p factors.
The
PV
function that
we
used in the last sec-
tion also calculates the
P value for a given A
over
n years, and a separate F value
TA BLE 2-2
PIA
and
AI
P Factors: Notation and Equations •
Factor
Factor
Standa
rd Excel
No
ta
ti
on
Name
Find/Given
Formula
Notation
Equatio
n F
unct
i
on
(PIA,i,n) Uniform-series
PIA
(1
+
0"
- 1
P =
A(PIA
,i,n)
PV(
i%,n,
A)
present worth
i(l
+
0"
(AIP
,i,n) Capital recovery
AlP
i(l
+ 0"
A =
P(AI
P,i,n)
PMT(i%,n,P)
(1+0"-1
SECTION 2.2
Uniform-Series
Present Worth Factor and Ca
pi
tal Recovery Factor
in
year n, if it is given.
The
format, introduced in Section 1.8, is
P
V(i%,
n
,A,F)
Similarly, the A value is determined using the
PMT
function for a given P value
in
year 0 and a separate F,
if
given.
The
format is
PMT
(i%,
n,P,F)
The
PMT
function was demonstrated in Section 1.18 (Figure 1-5b) and is used
in later examples. Table
2-2
includes the PV and
PMT
functions for P and A,
respectively. Example 2.4 demonstrates the
PV
function.
EXAMPLE
2.4
How
mu
ch money should you be willing to pay now for a guaranteed $600 per year for
9 years st
ar
ting next year, at a rate
of
return
of
16% per year? -
_ r---...,
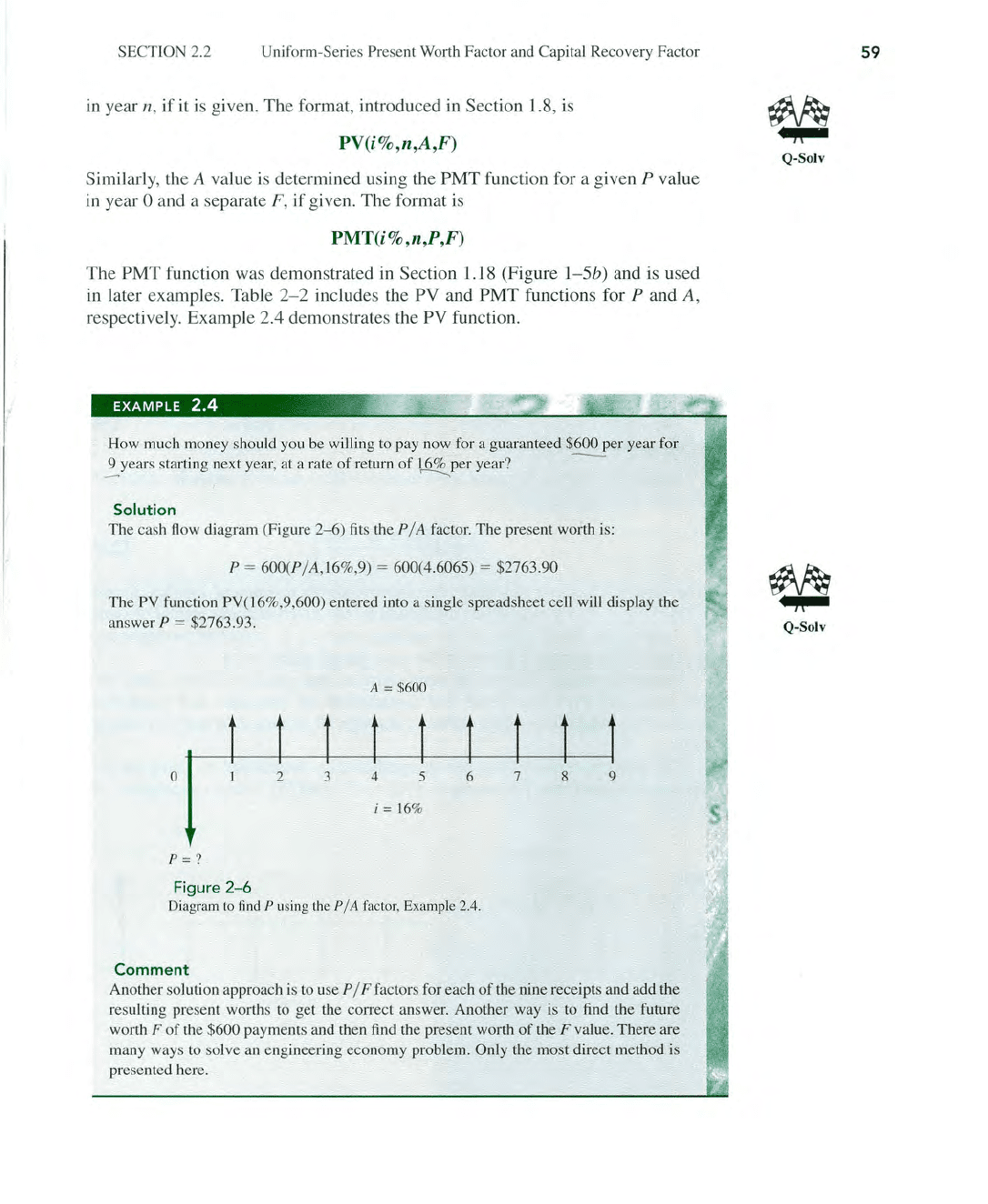
Solution
The
cash flow diagram (Figure
2-6
)
fits
the P / A factor. The present worth is:
P = 600(P/A,
16
%,9) = 600(4.6065) = $2763.90
The
PY function PY(J6%,9,600) entered into a single spreadsheet cell will
di
splay the
answer
P = $2763.93.
A =
$600
o
2 3
4
5 6 7
8
9
i=
16%
p=?
Figure
2-6
Diagram to find P using the P / A factor, Example 2.4.
Comment
Another solution approach is to use P / F factors for each
of
th
e nine receipts and add the
resulting present worths to get the correct answer. Another way is to find the future
worth
F
of
the $600 payments and
th
en find the present worth
of
the F value. There are
many ways
to
solve an eng
in
eering economy problem. Only the most direct method
is
presented here.
59
Q-So
lv
Q-
So
lv
i

60
0
2
CHAPTER 2
Factors: How Time and Interest Affect Money
2.3
SINKING FUND FACTOR
AND
UNIFORM-SERIES
COMPOUND
AMOUNT
FACTOR
(A
I F
AND
FI A)
The simplest way to derive the
AI
F factor is to substitute into factors already
developed.
If
P from Equation [2.3] is substituted into Equation [2.7], the fol-
lowing formula results.
[
I
J [
i(l
+ i)" J
A = F
(l
+ i)"
(l
+ i)" - 1
A - F [ (1 +
:r
-1 J
[2
.
8]
The expression in brackets
in
Equation [2.8] is the
AI
F or sinking fund factor.
It
determines the uniform annual series that
is
equivalent to a given future worth
F.
This
is
shown graphically in Figure 2-7a.
The uniform series A begins
at
the end
of
period 1
and
continues through
the period
oj
the given F.
Equation [2.8] can be rearranged to find F for a stated A series in periods 1
through
n (Figure 2-7b).
[
(1
+ i)" - 1 J
F = A .
1
[2.9]
The term in brackets is called the uniform-series compound amount Jactor
(USCAF), or F
I A factor. When multiplied by the given uniform annual amount
A, it yields the future worth
of
the uniform series. It is important
to
remember
that the future amount
F occurs in the same period as the last A.
Standard notation follows the same form as that
of
other factors. They are
(F
I A,i,n) and
(AI
F,i,n). Table
2-3
summarizes the notations and equations,
as
does the inside front cover. Tables 1 through 29 include F I A and
AI
F factor
values.
The
uniform-series factors can be symbolically determjned by using an ab-
breviated factor form. For example,
F I A =
(F
I P)(P I A), where cancellation
of
F =
g.
iven
F= ?
i =
give
n
i =
given
/1
-2
11
- 1
11
0
I
rr
f-
r
t
I
Figure
2-7
A
=?
(a)
Cash Aow
dia
grams to (a) find A,
given
F, and (b)
find
F,
given
A.
A
=
given
(b)

SECTION 2.3
Sinking Fund Factor and Uniform-Series Compound Amount Factor
TABLE
2-3
F I A and AI F Factors: Notation and Equations
Fa
ctor
Factor
Sta
ndard
N
ota
tion
Name Fi
nd/G
i
ven
Formula
Notat
ion Equ
ation
(FIA,i,n)
U nifonn-series
FIA
(l
+
i)"
- 1
F =
A(F
I
A,i,n)
compound amount
(AI
F,i,n)
Sinking fund
AIF
(l+i)"-l
A =
F(AI
F,i,n)
the P is correct. Using the factor formulas, we have
(
FIA
i n) =
[(
1 +
i)/]
=
-'-
.
--'----
[
(
1
+ i)" - 1 J
(1
+
i)n
- I
, ,
i(l
+
it
i
Also the
AIF
factor in Equation [2.8] may be derived from the
AlP
factor by
subtracting
i.
(AI
F,i,n) =
(AI
P,i,n) - i
This relation can be verified empirically in any interest factor table
in
the rear
of
the text, or mathematically by simplifying the equation to derive the
AI
F factor
formula. This relation is used later to compare alternatives by the annual worth
method.
For solution by computer, the FY spreadsheet function calculates
F for a
stated
A series over n years. The format
is
FV(i%,n,A,P)
The P may be omitted when no separate present worth value is given. The PMT
function determines the A value for n years, given F
in
year n, and possibly a sep-
arate
P value
in
year
O.
The format is
PMT(i
%
,n,P,F)
If
P
is
omitted, the comma must
be
entered so the computer knows the last entry
is
an F value. These functions are included in Table
2-3.
The next two examples
include the FY and
PMT
functions.
EXAMPLE
2.5
"}
Formasa Plast
ic
s has major fabrication plants
in
Texas and Hong Kong. The president
wants to know the equivalent future worth
of
a
$1
million capital investment each
year for 8 years, starting 1 year from now. Formasa capital eams at a rate
of
14
% per
year.
61
Excel
Functions
FV(i%,n,A)
PMT(i
%,n"F)
fII
Q·
Solv
62
Q-Solv
Q-Solv
CHAPTER 2
Factor
s:
How Time and Interest Affect Money
Solution
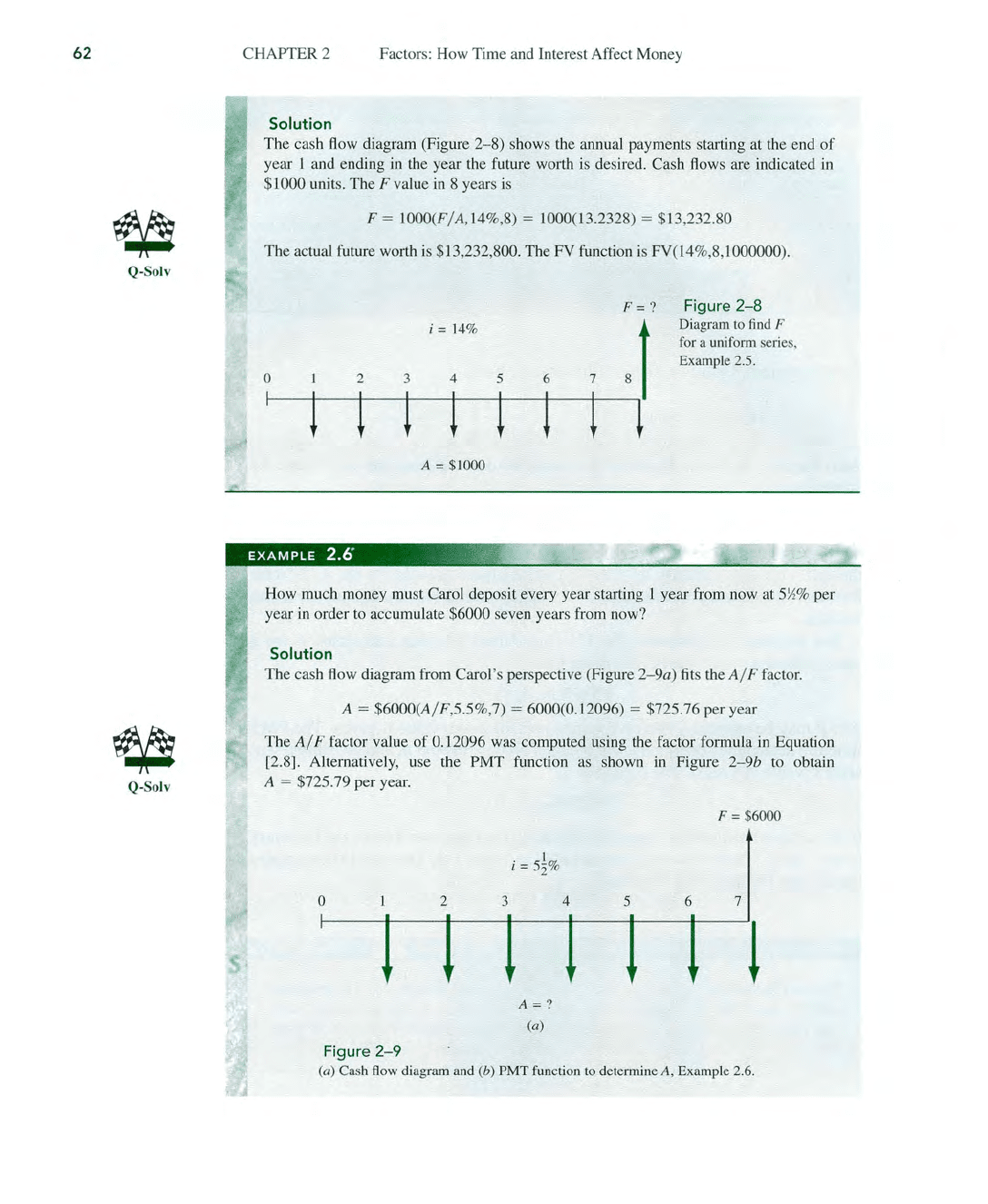
The cash
flow
diagram (Figure
2-8)
shows the annual payments starting at the end
of
year 1 and ending
in
the year the future worth
is
desired. Cash
flows
are indicated in
$1000 unit
s.
The F value in 8 years
is
F = 1000(F/A,
14
%,
8) = 1000(13.2328) = $13,232.80
The actual future worth
is
$13,232,800. The FY function is FY(14%,8,1000000).
i = 14%
2
3
4 5
6
7 o
I
t t t t t t t
A = $1000
EXAMPLE
2.0
~~
..
F=?
Figure
2-8
Diagram to find F
for a uniform series,
Example 2.5.
How
much money must Carol deposit every year starting 1 year from now at
5
~%
per
year
in
order
to
accumulate $6000 seven years from
now
?
Solution
The cash
flow
diagram from Carol's perspective (Figure 2-9a)
fits
the
A/F
factor.
A = $6000(A/F,5.5%,7) = 6000(0.12096) = $725.76 per year
The
A/F
factor value
of
0.12096 was computed using the factor formula
in
Equation
[2.8]. Alternatively, use the
PMT function
as
shown in Figure 2-9b
to
obtain
A = $725.79 per year.
F = $6000
o 2
3
4
5 6
7
l
A = ?
Ca)
Figure 2- 9
Ca)
Cash flow diagram and (
b)
PMT
function to determine A, Example 2.6.

SECTION 2.4
Interpolation in Interest Tables
Figure
2-9
(Con.tin.ued).
(b)
2.4
INTERPOLATION IN INTEREST
TABLES
When
it
is necessary to locate a factor value for an i
or
n
not
in the interest tables,
the desired
value
can be obtained in
one
of
two
ways: (1)
by
using
the
form
ulas
derived in Sections 2.1 to 2.3
or
(2) by linearly interpolating
between
the tabu-
lated values.
It
is generally easier
and
faster to use the formulas
from
a
calculator
or
spreadsheet that has
them
preprogrammed
. Furthermore, the value
obtained
through linear interpolation is not exactly correct, since the equations are nonlin-
ear
. Nevertheless, interpolation is sufficient in
most
cases as long as the values
of
i
or
n are not too distant
from
one
another.
The
first step in linear interpolation
is
to set up the
known
(values I and 2) and
unknown factors, as shown in Table
2-4. A ratio equation is
then
set
up
and
solved for c, as follows:
a c
b
d
or
c
=!!:...d
b
[2.10]
where
a, b, c, and d represent the differences
between
the
numbers
shown
in the
interest tables.
The
value
of
c
from
Equation [2.10] is
added
to
or
subtracted
from
value 1, depending on whether the factor is increasing
or
decreasing in val
ue
,
respectively.
The
following
examples
illustrate the
procedure
just
described.
TABLE
2-4
Linear Interpolation Setup
; or n
t:
-
~
tabulated
b 4 desired
tabulated
Factor
value 1
~
unlisted
~
C d
value 2
63

64
CHAPTER 2
Factors: How Time and Interest Affect Money
Determine the value
of
the
AlP
factor for
an
interest rate
of
7.3% and n
of
10
years, that
is
, (A I P,7.3%,
1O).
Solution
The va
lu
es
of
the Al P factor for interest rates
of
7 and 8% and n =
10
are
li
sted in
Tables
12
a
nd
13
, respectively.
~
7
%
b a 7.3%
8%
0.14238~
l
c
X d
0.14903
The unknown X is the desired factor value. From Equation [2.10],
c
= C 8
3
_-
77)(0.14903 - 0.14238)
= 0;3(0.00665) = 0.00199
Since the factor is increasing
in
value
as
the interest rate increases from 7
to
8%, the
va
lu
e
of
c
mu
st be added to the value
of
the 7% factor. Thus,
X = 0.14238 + 0.00199 = 0.14437
Comment
It
is
good practice to check the reasonableness
of
the final answer by verifying that X
lies between the values
of
the known factors
in
approximately the correct proportion
s.
Tn
thi
s case, since 0.14437 is less than 0.5
of
th
e distance between 0.14238 and 0.14903,
the answer seems reasonable.
If
Equation [2.7] is applied, the exact factor value
is
0.144358.
EXAMPLE 2.8
Find the value
of
the
(P
I F,4%
,48
) factor.
Solution
From Table 9 for 4% interest, the values
of
the
PI
F factor for 45 and 50 years are found.
0.1712~
C
X
~
d
0.1407
From Equation [2.10],
c
=
;(d)
=
~~
=
:~
(0.1712 - 0.1407) = 0.0183
