Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

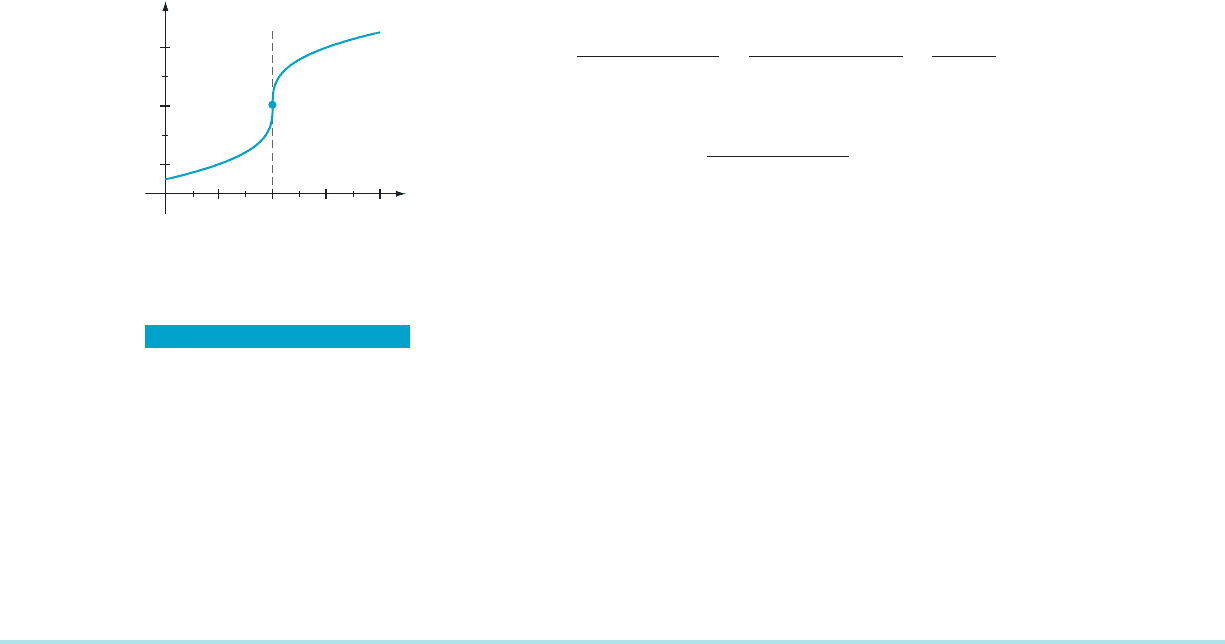
Our ﬁnal example concerns a function for which formula (3.1.11) does not

evaluate to a ﬁnite limit.

⁄ EX

AMPLE 12 Discuss the tangent line of f ðxÞ5 3 1 ðx22Þ

1=3

at the point

P 5 (2, 3).

Solution Becau

f ð2 1 ΔxÞ2 f ð2Þ

Δx

3 1 ðΔ x Þ

1=3



2 3

Δx

ðΔxÞ

2=3

;

we may use Theorem 5 of Section 2.2 to conclude that

lim

Δx-0

f ð2 1 ΔxÞ2 f ð2Þ

Δx

51N:

Our deﬁnition of tangent line therefore does not apply. Nevertheless, the graph of

f (Figure 13) indi cates that f has a vertical tangent line, x 5 2, at P. It is possible

to develop the concept of the tangent line to include vertical tangent lines, but

because we do not need the greater generality, we will not do so.

QUICK QUIZ

1. A particle moves along an axis with position p(t) 5 4t

at time t. What is its

velocity when t 5 3?

2. The position of a particle moving along the x-axis is 24t 2 2t

at time t. For what

values of t is the particle moving to the left?

3. What is the instantaneous rate of change of the area of a circle with respect to its

radius when its circumference is 10?

4. What is the tangent line to the graph of y 5 2x

1 3 at the point (21, 1)?

Answers

1. 24 2. ð2 N; 2 2Þ,ð2; NÞ 3.

10 4. y 5 6(x 1 1) 1 1

4231

f(x)  3  (x  2)

13

P  (2, 3)

m Figure 13

EXERCISES

Problems for Practice

c In Exercises 112, p(t) describes the position of an object

at time t. Calculate the instantaneous velocity at time c. b

1. pðtÞ5 5 c 5 2

2. pðtÞ523tc5 5

3. pðtÞ527t

c 5 3

4. pðtÞ524t

c 5 2

5. pðtÞ5 6t 1 8 c 5 3

6. pðtÞ525t

1 2 c 5 1

7. pðtÞ5 2t

2 17tc5 2

8. pðtÞ5 2t

2 3t

c 521

9. pðtÞ5 t

2 6t 1 10 c 5 2

10. pðtÞ5 t

1 2t

1 3t 1 4 c 5 2

11. pðtÞ5 1=tc5 1=2

12. pðtÞ5 2t 2 3=tc5 3

c In Exercises 1316, p(t)

describes the position of a moving

body at time t. Determine whether, at time t 5 4, the body is

moving forward, backward, or neither. b

13. pðtÞ5 6t 1 3

14. pðtÞ5 t

2 8t

15. pðtÞ52t

1 5t

16. pðtÞ5 1=t

c In each of Exercises 1720, a function f and

a point c are

given. Calculate f

ðcÞ. b

17. f ðxÞ5 5x

2 21xc5 3

18. f ðxÞ5 2x

1 3x

c 523

19. f ðxÞ5 3x

1 2=xc522

20. f ðxÞ5 5x

1 4x

1 3x 1 2 c 522

3.1 Rates of Change and Tangent Lines 175

c In Exercises 2124, ﬁnd the slope of the tangent line to the

graph of the given function at the given point P. b

21. f ðxÞ5 x

P 5 ð3; 9Þ

22. f ðxÞ5 x

2 2xP5 ð1; 21Þ

23. f ðxÞ5 3x

1 6 P 5 ð21; 9Þ

24. f ðxÞ524x

1 x 1 1 P 5 ð2; 213Þ

c In each of Exercises 2528, a function f and

a point P are

given. Find the point-slope form of the equation of the tan-

gent line to the graph of f at P. b

25. f ðxÞ5 2x

P 5 ð5; 50Þ

26. f ðxÞ5 x

=6 P 5 ð2; 4=3Þ

27. f ðxÞ523x

1 5 P 5 ð2 2; 2 7Þ

28. f ðxÞ5 1=xP5 ð2 1; 2 1Þ

c In each of Exercises 2932, a function f and

a point P are

given. Find the slope-intercept form of the equation of the

tangent line to the graph of f at P. b

29. f ðxÞ5 5x

P 5 ð2; 20Þ

30. f ðxÞ5 x

=3 P 5 ð2 3; 2 9Þ

31. f ðxÞ5 3x

1 2xP5 ð1; 5Þ

32. f ðxÞ5 2x 2 2=xP5 ð2 1=2; 3Þ

c In each of Exercises 3336, a function f and

a point P are

given. Find the point-slope form of the equation of the nor-

mal line to the graph of f at P. b

33. f ðxÞ5 2x

P 5 ð5; 50Þ

34. f ðxÞ5 x

=6 P 5 ð2; 4=3Þ

35. f ðxÞ523x

1 5 P 5 ð2 2; 2 7Þ

36. f ðxÞ5 1=xP5 ð2 1; 2 1Þ

c In each of Exercises 3740, a function f and

a point P are

given. Find the slope-intercept form of the equation of the

normal line to the graph of f at P. b

37. f ðxÞ5 3x

P 5 ð2 1; 3Þ

38. f ðxÞ5 x

=2 P 5 ð2; 4Þ

39. f ðxÞ5 3x

2 2x

2 10 P 5 ð2; 6Þ

40. f ðxÞ5 x

2 3=xP5 ð2 3; 10Þ

Further Theory and Practice

41. The instantaneous rate of change of velocity is accel-

eration. For the position function p(t) 5 t

, what is the

acceleration at time t 5 1?

42. The population of a colony of bacteria after t hours is

B(t) 5 5000 1 6t

. At what rate is the population changing

after 2 hours?

43. If C(x) is the cost of producing x units of an item, then the

marginal cost of the x

item is deﬁned to be C

(x).

Suppose that the cost in cents of producing x pencils is

CðxÞ5 5 1 0:1x 2 0:001x

for x # 50. What is the marginal

cost when x 5 25?

44. A large herd of reindeer is dying out. The number of

reindeer in the herd at time t (measured in months),

0 # t # 15, is

rðtÞ5 25000 2 800t 2 40t

2 t

At what rate are the reindeer dying out after 11 months?

c In Exercises 4550, p(t)

describes the position of an object

at time t. Calculate the instantaneous velocity at time c. b

45. pðtÞ5 tðt 1 1Þ c 5 2

46. pðtÞ5 t

ð2t 2 3Þ c 5 3

47. pðtÞ5 t

ð3 2 2=tÞ c 5 3

48. pðtÞ5 ð t 1 2Þðt 1 3Þ c 521

49. pðtÞ5 ð t

1 9Þ=tc5 2

50. pðtÞ5 tðt 1 1Þðt 1 2Þ c 5 2

c In Exercises 5154, ﬁnd a line that is tangent to the graph

the given function f and that is parallel to the line

y 5 12x. b

51. f ðxÞ5 3x

1 1

52. f ðxÞ5 x

2 4x 1 2

53. f ðxÞ5 x

2 15x 1 20

54. f ðxÞ5 11x 2 4=x

55. Six points are labeled on the graph of the function f in

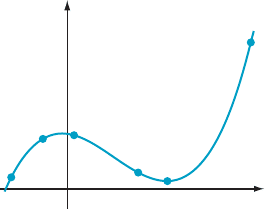
Figure 14. The instantaneous rates of change of f with

respect to x at the six points are 23, 21, 0, 3, 10, and 20.

Match each point to the corresponding rate of change.

56. What is the rate of change of the area of a square with

respect to its side length when the side length is 8

centimeters?

57. What is the rate of growth of the surface area of a sphere

with respect to the radius when the radius is 8 inches?

(The surface area of a sphere of radius r is 4πr

58. What is the rate of change of the area of an equilateral

triangle with respect to its side length when that side

length is 8 inches?

59. Let p(t) 5 t

1 t denote the position of a moving body.

Determine for which values of t the velocity of the body is

positive and for which values of t the velocity is negative.

m Figure 14

176 Chapter

3 The Derivative

60. Let p(t) 5 t

26t

denote the position of a moving body.

Determine for which values of t the velocity of the body is

positive and for which values of t the velocity is negative.

61. Find the equation of the line that is tangent to the graph

of f (x) 5 3x

1 12 and that passes through the origin.

62. Find the equations of the tangent lines to the graph of

f (x) 5 3x

that pass through the point (1, 29).

63. Let f (x) 5 x

. For what value(s) of c does the tangent line

to the graph of f at (c, f (c)) pass through the point (3, 5)?

64. For what values of A and C does the graph of y 5 Ax

1 C

pass through the point P 5 (1, 1) and have the same

tangent line at P as the graph of y 5 x

65. Find the points on the graph of the function

f ðxÞ5 x

2 2x

2 8x 1 3 at which the tangent line is par-

allel to the graph of y 5 4 2 9x.

66. Find all values of c for which the tangent lines to the

graphs of f ðxÞ5 x

2 7x 1 9 and gðxÞ5 9=x at ðc; f ðcÞÞ and

ðc; gðcÞÞ are parallel.

67. Find all values of c for which the tangent lines to the

graphs of f (x) 5 x

2 8x 1 3 and g(x) 5 4/x at (c, f (c)) and

(c, g(c)) are parallel.

68. Let f (x) 5 x

, and suppose that a and b are different

constants. Find a formula for the point of intersection of

the tangent line to the graph of f at x 5 a and the tangent

line to the graph of f at x 5 b.

69. Suppose that c is a positive constant. Let L

be the line

that is tangent to the graph of f (x) 5 1/ x at P 5 (c,1/c).

Show that the area of the triangle formed by L

and the

positive axes is independent of c. Compute that area.

70. At Wrigley ﬁeld in Chicago, Cubs fans throw the ball

back onto the ﬁeld when a visiting team hits a home run.

Suppose that the height H above ﬁeld level of a ball

thrown back by a Cubs fan is given in feet by

HðtÞ5 18 1 13:8t 2 16t

when t is measured in seconds.

a. How high above ﬁeld level is the fan sitting?

b. What is the rate at which the ball rises as a function of

time?

c. At what time does the ball reach its maximum height?

What is this maximum height?

d. What is the average rate of change of H during the

ball’s upward trajectory?

e. How long is the ball in the air?

f. What is the rate of change of H at the moment the ball

hits the ground?

g. What is the average rate of change of H over the

entire trajectory of the ball?

71. Suppose a 6¼0. What relationship between a and b is a

necessary and sufﬁcient condition for the graph of

f (x) 5 ax

1b to have a tangent line that passes through the

origin?

72. Suppose that f is a function whose graph has a tangent

line at each point. If g(x) 5 f (x) 1 α for some constant α,

show that the graph of g has a tangent line at each point

and that the slope of the tangent line to the graph of g at

(c, g(c)) is the same as the slope of the tangent line to the

graph of f at (c, f (c)). Explain this geometrically.

73. Let f (x) be a quadratic polynomial. Show that the tan-

gent line to the graph of f at any point P can only

intersect the graph of f at P.

74. Finding a function from the tangent lines to its graph. If f

is a continuous function with f (2) 5 5, and if the slope

of the tangent line to the graph of f at ðc; f ðcÞÞ is 22 for

2N , c , 1; 1 for 1 , c , 3, and 21 for 3 , c , N, ﬁnd

f .

75. Suppose

that f is deﬁned on an open interval centered

at c. Suppose also that

‘

5 lim

h-0

f ðc 1 hÞ2 f ðcÞ

and

‘

5 lim

h-0

f ðc 1 hÞ2 f ðcÞ

exist. Let

ðxÞ5 f ðcÞ1 ‘

ðx 2 cÞ for x $ c

ðxÞ5 f ðcÞ1 ‘

ðx 2 cÞ for x # c:

Deﬁne α

through which T

must be rotated counterclockwise

about (c, f (c)) to coincide with T

. We may think of α

(c)

as the angle of the corner at P 5 (c, f (c)).

a. For what values of α

at P? Explain.

b. For what value of α

Explain.

c. If the graph of f has a vertical tangent at P,isα

(c)

deﬁned? Explain.

76. Suppose that the graph of f has a nonvertical tangent T

each point P on it. Thus for each P there are two numbers

m(P) and b(P) such that T

(x) 5 m(P) x 1 b(P).

a. Deﬁne the “tangents to the graph of f at inﬁnity and

minus inﬁnity,” lim

P-N

and lim

P-2N

,inan

appropriate way.

b. Show that if f (x) 5 1/x, then lim

P-N

and

lim

P-2N

are horizontal asymptotes of the graph

of f.

c. Is the converse to (b) true? Think of f (x) 5 sin (x)/x.

Explain your answer.

Calculator/Computer Exercises

77. The trajectory of a ﬂy ball is such that the height in feet

above ground is H(t) 5 4 1 72t 2 16t

when t is measured

in seconds.

a. Compute the average velocity in the following time

intervals:

i. ½2; 3

ii. ½2; 2:1

iii. ½2; 2:01

iv. ½2; 2:001

b. Compute the instantaneous velocity at t 5 2.

3.1 Rates of Change and Tangent Lines 177

78. For the trajectory in the preceding problem,

a. Compute the average velocity in the following time

intervals:

i. ½3; 3:1

ii. ½3; 3:01

iii. ½2:9; 3

iv. ½2:99; 3

b. Compute the instantaneous velocity at t 5 3.

79. The position of an oscillating body is given by p(t) 5

sin (2t 1 π/6). Calculate the average velocity of the body

over a time interval of the form ½0; Δt for Δt 5 10

n 5 0; 1; 2; 3 and 4. Display your results in the form of a

table. Formulate a guess v for the instantaneous velocity

of the body at time t 5 0. Plot p. In the same coordinate

plane, add the graph of the straight line that passes

through (0, 1/2) and that has slope v. Does the resulting

ﬁgure support your conjectured value? Explain.

80. The position of a moving body is given by p(t) 5

(2.718281828)

. Calculate the average velocity of the body

over a time interval of the form ½1; 1 1 Δt  for a sequence

of small values of Δt. Display your results in the form of

a table. Formulate a guess m for the instantaneous velo-

city of the body at time t 5 1. Plot p. In the same coordi-

nate plane, add the graph of the straight line that passes

through (1, 2.718281828) and that has slope m. Does the

resulting ﬁgure support your conjectured value? Explain.

81. Repeat the preceding exercise with t 5 2 and t 5 3. What

is the apparent relationship between the position of the

body p(t) and the instantaneous velocity at t?

82. Graph the function f (x) 5 x/(x 1 1), and zoom in on

the point (22, 2). Formulate a guess for the slope of the

tangent line L at that point. Now examine the quotient

( f (22 1 Δx) 2 f (22))/Δx for various small values of Δx.

Display your results in a table. Use this data to estimate

the slope of L. How do your visual and numerical esti-

mates compare?

83. Repeat the preceding exercise for the function f (x) 5

tan (x) at the point (π/4, 1).

84. Suppose that a .

0. Tangent lines to the exponential

functions f (x) 5 a

are investigated in this exercise.

a. Use the formula for the slope of a tangent line to show

that the slope of the tangent line to f at (c, f (c)) is

ðcÞ5 a

lim

h-0

2 1

b. Show that the slope of the tangent line to f at (0, 1) is

lim

h-0

2 1

c. This limit cannot be computed by substituting h 5 0in

the expression because that results in the meaningless

expression 0/0. We will learn how to compute this

limit in Section 3.6. For now, we will investigate it

numerically. To be speciﬁc, let a 5 2. To identify the

limit, graph the function h/ð2

2 1Þ=h in a window

whose horizontal range is a small interval centered at

0. From the graph (zooming in if necessary), identify

lim

h-0

2 1

to four decimal places.

d. Graph f (x) 5 2

tangent lines to the graph of f at (0, 1)

and (2, 4) in the same viewing window.

e. Repeat parts (c) and (d) with a 5 3. Use (21, 1/3) and

(1, 3) as the points of tangency.

3.2 The Derivative

In Section 3.1, we saw that the limit

ðcÞ5 lim

Δx-0

f ðc 1 Δ x Þ2 f ðcÞ

Δx

represents the instantaneous rate of change of the function f at the point c.Itis

also the slope of the tangent line to the graph of f at (c, f (c)). Later in this chapter,

and especially in Chapter 4 and beyond, we will see many other applications

of this limit. Because of its importance, we give it a name and study ways to

evaluate it.

178 Chapter 3 The Derivative

DEFINITION

Let f be a funct ion that is deﬁned in an open interval that

contains a point c. If the limit

lim

Δx-0

f ðc 1 ΔxÞ2 f ðcÞ

Δx

exists and is ﬁnite, then we say that f is differentiable at c. We call this limit the

derivative of the function f at the point c, and we denote it by the symbol f

ðcÞ,as

in Section 3.1:

ðcÞ5 lim

Δx-0

f ðc 1 ΔxÞ2 f ðc Þ

Δx

ð3:2:1Þ

The process of calculating f

ðcÞ is called differentiation.

INSIGHT

The property of differentiability can also be stated in geometric terms: the

function f is differentiable at c if and only if the graph of f has a nonvertical tangent

line at the point (c, f (c)).

It is often convenient to express f

ðcÞ by means of formulas that differ somewhat

from (3.2.1). For example, the letter h is often used instead of Δx to indicate an

increment:

ðcÞ5 lim

h-0

f ðc 1 hÞ2 f ðcÞ

: ð3:2:2Þ

Also, if we set x 5 c 1 Δx, then Δx 5 x 2 c and

f ðc 1 ΔxÞ2 f ð cÞ

Δx

f ðxÞ2 f ðcÞ

x 2 c

The statement Δx - 0 is equivalent to x-c. Thus the deﬁnition of the derivative of

f at c can be stated as

ðcÞ5 lim

x-c

f ðxÞ2 f ðcÞ

x 2 c

: ð3:2:3Þ

In Section 3.1 we calculated f

ðcÞ for several functions. For now, if f is not one

of the functions we have studied, we must compute f

ðcÞ by referring to deﬁnition

(3.2.1). Our ﬁrst example is an illustration of such a calculation.

⁄ EX

AMPLE 1 Calculate f

(5) for f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4x 2 11

Solution Here c 5 5.

Starting from formula (3.2.1), we have

ð5Þ 5 lim

Δx-0

f ð5 1 ΔxÞ2 f ð5Þ

Δx

5 lim

Δx-0

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4ð5 1 ΔxÞ2 11

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4ð5Þ2 11

Δx

5 lim

Δx-0

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 1 4Δx

2 3

Δx

3.2 The Derivative 179

5 lim

Δx-0



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 1 4Δx

1 3Þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 1 4Δx

1 3



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 1 4Δx

2 3

Δx



5 lim

Δx-0

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 1 4Δx

2 3

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 1 4Δx

1 3ÞΔx

5 lim

Δx-0

9 1 4Δx 2 9

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 1 4Δx

1 3ÞΔx

5 4 lim

Δx-0

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 1 4Δx

1 3

5 4 

3 1 3

;

or f

(5) 5 2/3. ¥

INSIGHT

As Example 1 demonstrates, calculating a derivative by working directly

from deﬁnition (3.2.1) may require several algebraic steps and some specialized

manipulations. One of the goals of this chapter is to develop formulas that enable us to

calculate derivatives easily, without referring to the limit deﬁnition.

Other Notations for the

Derivative

There are several alternative notations for the derivative f

(c)off at c. For

example, f

ðcÞ is often denoted by D( f )(c). Leibniz notation, which is named after

Gottfried Wilhelm von Leibniz (16461716), one of the coinventors of calculus, is

also widely used. It can take the following forms

ðcÞ or



x5c

(The vertical bar with subscript x 5 c to denote evaluation at c was introduced in

the 19

century.) One advantage of Leibniz notation over f

ðcÞ is that Leibniz

notation tells us explicitly what the variable of differentiation is (in this case it is x).

This reminder can be helpful when several variables are under simultaneous con-

sideration. It is also a suggestive notation. After all, if we let Δf denote the

increment f (c 1 Δx) 2 f (c), then

ðcÞ5 lim

Δx-0

f ðc 1 Δ x Þ2 f ðcÞ

Δx

5 lim

Δx-0

Δf

Δx

: ð3:2:4Þ

To Leibniz, the symbol df/dx in (3.2.4) actually represented a ratio of inﬁnitesimal

quantities df and dx. These quantities are known as differentials, but we will not

give any meani ng to them as separate inﬁnitesimal entities. Later we will ﬁnd

that there are circumstances in which manipulation of these differentials will be

useful.

A curve C in the xy-plane is not necessarily the graph of a function. But such a

curve can still have a tangent line. When we think of the variables x and y as being

related by virtue of the ordered pair (x, y) being on the curve C, we write

ðx

Þ or



ðx

; y

ð3:2:5Þ

180 Chapter 3 The Derivative

for the slope of a tangent line to the curve at the point (x

, y

) A C. If there is more

than one value of y such that (x

, y)isonC, then the second expression in (3.2.5)

should be used—see Figure 1.

In the case that g is a function of the time variable t, then we sometimes adopt

the Newton notation and write the derivative as

g(t). This notational device is

named after Sir Isaac Newton (16421727), the other coinventor of calculus.

Newton’s notation is commonly used in physics today.

The Derived Function If f has a derivative at every point of S, then we say that f is differentiable on S.In

the most common situation that is encountered in this text, S is an open interval. If f

is differentiable on S, then we can form a function f

on S that is deﬁned by

ðxÞ5 lim

Δx-0

f ðx 1 ΔxÞ2 f ðxÞ

Δx

for x 2 A S:

This function f

is said to be the derived function of f or the derivative of f. Other

notations for this function are

f and Dðf Þ:

INSIGHT

The two expressions

ðxÞ and

f ðxÞ

mean the same thing. However, some care must be taken when using Leibniz notation to

signify a derivative at a ﬁxed point c in the domain of f

. The expression

f ðcÞ can cause

confusion about the order in which the operations of differentiation and evaluation

are performed. Does the expression

f ðcÞ mean that x should be set equal to c in

f ðxÞ?

Or does

f ðcÞ signify that the constant f (c) should be differentiated with respect to x?

These different interpretations generally lead to different results. The ambiguity can be

avoided by using one of the following notations:

ðcÞ or

f ðxÞ



x5c



x5c

The vertical bar notation is especially clear in signifying that evaluation is the ﬁnal

operation.

, y

)

Slope 

m Figure 1

, y

)

, y

)

Slope 

3.2 The Derivative 181

Differentiability and

Continuity

Continuity and differentiability are properties of a function that are reﬂected

in its graph. Suppose that f is deﬁned on an open interval containing c, and let P 5

(c, f (c)). If f is continuous at c, then we know that if we follow the points

(x, f (x)) as x - c, those points approach P. Continuity may be interpreted as

predictability.

We also know that, when a function f is differentiable at c, then its graph has

a well-deﬁned tangent line at P. Differentiability may be interpreted as a degree

of smoothness. This is a stronger property than predictability. If f is discontinuous

at c, then Figure 2 suggests that there is no line that is tangent to the graph of f at P.

In that ﬁgure, line L through P is the only candidate to be a tangent line. However,

line L cannot be regarded as a tangent line because it does not have one of the

properties we expect from a tangent line: for x just to the left of c, the point

ðx; f ðxÞÞ on the graph of f is not near to L. We state our conclusions as a theorem.

THEOREM 1

If f is not continuous at a point c in its domain, then f is not

differentiable at c. In other words, if f is differentiable at a point c in its domain,

then f is continuous at c.

Proof. The

two statements of the theorem are logically equivalent. We prove the

second. To that end, suppose that f is differentiable at a point c in its domain. Using

formula (3.2.3) for f

ðcÞ, we see that lim

x-c

ðf ðxÞ2 f ðcÞÞ=ðx 2 cÞ exists. Because

lim

x-c

ðx 2 cÞ5 0, we conclude that lim

x-c

ðf ðxÞ2 f ðcÞÞ5 0 by Theorem 5 of

Section 2.2. Therefore lim

x-c

f ðxÞ5 f ðcÞ: ’

Theorem 1 guarantees that, if f is

differentiable on an interval (a, b), then f is

also continuous on (a, b). Continuous functions, however, are not necessarily dif-

ferentiable. For example, the graph of f ðxÞ5 3 1 ðx22Þ

1=3

has a vertical tangent at

P 5 (2, 3) (Example 12, Section 3.1). This implies that f is not differentiable at x 5 2,

even though f is continuous there. Corners are also points of continuity but not

differentiability. Here is a simple example.

⁄ EX

AMPLE 2 Let f (x) 5 |x|. Certainly f is continuous at all points. Show

that f

(0) does not exist.

Solution The

relevant limit as Δx - 0 through positive values, is

lim

Δx-0

f ð0 1 ΔxÞ2 f ð0Þ

Δx

5 lim

Δx-0

jΔxj2 0

Δx

5 lim

Δx-0

Δx

5 lim

Δx-0

5 1:

But, as Δx - 0 through negative values, the limit is

Discontinuity at c

Not a tangent line

m Figure 2

182 Chapter

3 The Derivative

lim

Δx-0

f ð0 1 ΔxÞ2 f ð0Þ

Δx

5 lim

Δx-0

jΔxj2 0

Δx

5 lim

Δx-0

2 Δx

Δx

5 lim

Δx-0

2 1

521:

Because the left and right limits do not agree, the limit does not exist. Therefore

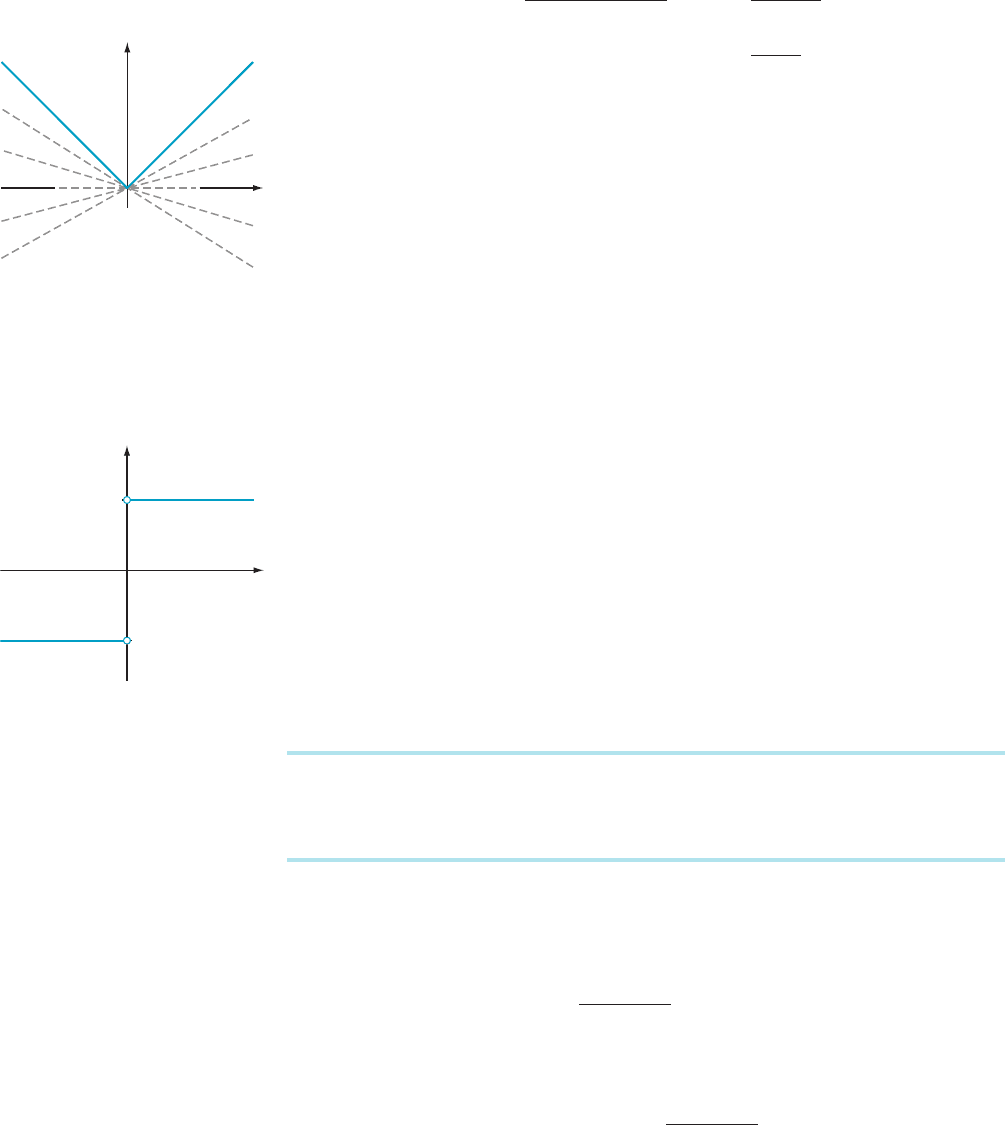
the derivative does not exist at 0. The fact that the function f (x) 5 |x| does not have

a derivative at x 5 0 has a simple geometrical interpretation: the dotted lines in

Figure 3 show that there is no geometrically satisfactory way of deﬁning a tangent

line to the graph of f at (0, 0). This signiﬁes that f

(0) does not exist. ¥

The domain of a derived function f

is the subset of the domain of f that is

obtained by removing the points where f is not differentiable. The domain of f

can

be smaller than the domain of f.

⁄ EX

AMPLE 3 Let f (x ) 5 |x|. Com pletely describe the function f

Solution Examp

le 2 shows that f

(0) does not exist. Therefore 0 is not in the

domain of f

.Ifx . 0, then the graph of f near the point (x, f (x)) is just a straight

line segment of slope 1. If x , 0, then the graph of f near the point (x, f (x)) is just a

straight line segment of slope 21. These considerations suggest that f

(x) 5 1 for

x . 0, and f

(x)521 for x , 0, as can be veriﬁed using the limit deﬁnition of f

(x).

We conclude that the domain of the derived function f

is the union (2N,0),

(0, N) of the two open half-lines to the left and right of 0 and

ðxÞ5

2 1ifx , 0

1ifx . 0



The graph of f

appears in Figure 4. ¥

b A LOOK BACK Differentiability is a stronger property than continuity (Theorem

1). Continuous functions are appealing for their predictability. Differentiable

functions have this predictability and a powerful geometric property: a well-deﬁned

tangent.

Investigating

Differentiability

Graphically

To use graphing techniques to examine the differentiability of a continuous func-

tion f at a point c, we deﬁne a new function φ by

φðxÞ5

f ðxÞ2 f ðcÞ

x 2 c

for x 6¼ c:

Then φ is a continuous function, but the point c is not in its domain. In Section 2.3,

we learned that φ can be continuously extended at c if and only if

lim

x-c

φðxÞ5 lim

x-c

f ðxÞ2 f ðcÞ

x 2 c

f

1

m Figure 4 The graph of f

where f(x) 5 |x|

f (x)  x

m Figure 3

3.2 The Derivative 183

exists. In view of formula (3.2.3) for f

ðcÞ, we can restate our conclusion as follows:

The function f is differentiable at c if and only if φ can be continuously

extended at c.

We can often use a graphing calc ulator or software to decide whether or not φ can

be continuously extended and, therefore, whether or not f is differentiable at c. The

next example illustrates these ideas.

⁄ EX

AMPLE 4 Determine whether or not the functions

ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 cosðxÞ

and f

ðxÞ5

xsinð1=xÞ if x 6¼ 0

0ifx 5 0



are differentiable at x 5 0.

Solution The

graph of f

, exhibited in Figure 5, does not seem to be smooth at

x 5 0. This suggests that f

is not differentiable at x 5 0. Let

ðxÞ5

ðxÞ2 f

ð0Þ

x 2 0

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 cosðxÞ

2 0

x 2 0

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 cos ðxÞ

for x 6¼ 0:

The graph of φ

, seen in Figure 6, shows that φ

(x) cannot be continuously

extended to x 5 0. This conﬁrms that f

is not differentiable at x 5 0.

The graph of f

in Figure 7 indicates that f is continuous at x 5 0, but differ-

entiability is far from transparent. Let

ðxÞ5

xsinð1=xÞ2 0

x 2 0

5 sin





for x 6¼ 0 :

It is evident from the graph of φ

(Figure 8) that φ

cannot be continuously

extended at x 5 0. This shows that f

is not differentiable at x 5 0. ¥

Derivatives of Sine

and Cosine

In Section 2.2 (Theorem 8 and Example 8), we went to some trouble to obtain the

limit formulas

lim

Δx-0

sinðΔxÞ

Δx

5 1 and lim

Δx-0



1 2 cosðΔxÞ

Δx



5 0:

ð3:2:6Þ

These limit formulas can now be used to evaluate the derivatives of sine and cosine.

THEOREM 2

For each x,

sinðxÞ5 cos ðxÞð3:2:7Þ

and

cosðxÞ52sinðxÞ: ð3:2:8Þ

0.5

1.0

1.5

22

(x)  1  cos(x)



m Figure 5

0.5

0.5

22

(x) 

 cos(x)



m Figure 6

0.05

0.05

0.10.1

(x)  x sin



m Figure 7

1.0

0.10.1

1.0

1.0

(x)  sin



m Figure 8

184 Chapter

3 The Derivative