Blanchet L., Spallicci A., Whiting B. (Eds.) Mass and Motion in General Relativity

Подождите немного. Документ загружается.

Constructing the Self-Force 321

8 Self-Force

Let us now reﬂect on the results of the preceding section and try to make sense of

Eq. 12 as an equation of motion for the particle. Our ﬁrst attempt will be entirely

heuristic; we shall add reﬁnement to our treatment in the following section.

Given that Eq. 12 does not make sense as it stands when we insert ˚ D ˚

ret

on its right-hand side, let us take the view that the equation is meant to apply to

an extended body instead of a point particle, and let us average ˚



WD r



˚ over

the body’s volume. This operation should be carried out in the body’s rest frame,

and for this purpose it is natural to adopt the Fermi coordinates. We aim, therefore,

to average the spatial components ˚

ret

of the ﬁeld gradient. The simplest form of

averaging was carried out already in the preceding section, and we obtained

h˚

ret

iDh˚

iCh˚

iD





C ˚

C O.s/; (26)

in which ˚

is evaluated (without obstacle) at s D 0. This expression corresponds

to pretending that the body is a thin spherical shell of radius s.

Substitution into Eq. 12 and evaluation in the Fermi coordinates produces

.m Cım/a

D q˚

; (27)

with ım WD q

=.3s/ denoting the contribution to the total body mass that comes

from the ﬁeld’s energy. Absorbing this into a redeﬁnition of the inertial mass m,the

ﬁnal tensorial expression for the equation of motion is

D q



˛ˇ

C u



; (28)

with

q Pa

C q



1

V.x;z/d

: (29)

This is Quinn’s equation of motion [10] for a scalar charge q moving in a curved

spacetime with metric g

˛ˇ

. The self-force involves an instantaneous term propor-

tional to Pa

D Da

=d , as well as an integral over the particle’s past history.

Equation 28 informs us that of the complete retarded ﬁeld ˚

ret

D ˚

C˚

, only

the Detweiler–Whiting regular ﬁeld ˚

contributes to the self-force. The role of the

singular ﬁeld is merely to contribute to the particle’s inertia, through a shift ım in

its inertial mass. This contribution diverges in the limit s ! 0, but it would be ﬁnite

for any extended body.

I must confess that this computation returns the wrong expression for the

particle’s self-energy. We obtained ım D q

=.3s/, while the correct expression

is ım D q

=.2s/; we are wrong by a factor of 2=3. I believe that this discrepancy

originates in an inconsistency between our assumed shape for the extended body –

a spherical shell of radius s – and the ﬁeld it produces, which we took to be equal to

322 E. Poisson

the ﬁeld produced by a point particle. I would conjecture that calculating the ﬁeld

actually produced by a spherical shell would give rise to the correct expression for

ım, but leave unchanged the ﬁnal result of Eq. 28 for the equation of motion.

9 Axiomatic Approach

The procedure outlined above is admittedly heuristic. It can, however, be formalized

and put on an axiomatic basis that supplies Eq.28 with a much improved pedigree.

This is the approach that was ﬁrst pursued by Ted Quinn and Bob Wald [10, 11].

They formulate two axioms that the scalar self-force F

should satisfy:

Quinn–Wald Axiom 1 Two scalar particles move on world lines  and Q in two

different spacetimes. At points z and Qz their acceleration vectors have equal lengths.

The neighborhoods of z and Qz, as well as the acceleration vectors, are identiﬁed in

Fermi coordinates. Then the difference in the self-forces is given by



D q



˛ˇ

C u



lim

s!0



: (30)

Here ˚ and

˚ are the retarded ﬁelds in each spacetime, and ˚

WD r

˚ while

˚. The limit is well deﬁned after the difference of ﬁeld gradients is

averaged over a sphere of radius s.

Quinn–Wald Axiom 2

D 0 in ﬂat spacetime, for a particle with uniform ac-

celeration.

The ﬁrst axiom is essentially a statement that when two particles momentarily

share the same acceleration, their ﬁelds are equally singular, and the difference (af-

ter averaging) possesses a well-deﬁned limit when s !0. The second axiom is a

scalar-charge analogue to a well-known result from ﬂat-spacetime electrodynamics:

a charged particle moving with a uniform acceleration does not undergo radiation

reaction.

According to Eq. 24, the curved-spacetime expression for the gradient of the

retarded ﬁeld is

D





 !



0b0c



0a0b

C O.s/I (31)

this holds at time t in Fermi coordinates. The ﬂat-spacetime expression is

D





 !



C O.s/; (32)

and this also holds at time t in the same system of Fermi coordinates. Under the con-

ditions of the Quinn–Wald axioms, the acceleration a

that appears in ˚

and

one and the same. In the ﬂat-spacetime expression we set Pa

and Pa

to zero because

Constructing the Self-Force 323

the acceleration is chosen to be uniform. In addition we eliminate the Riemann-

tensor terms, as well as the integral over the particle’s past history – V necessarily

vanishes in ﬂat spacetime.

Subtraction yields



0b0c



0a0b

C O.s/; (33)

and we get



C O.s/ (34)

after averaging over a sphere of constant s. The difference in the self-forces is there-

fore F



D qr

. The second axiom ﬁnally returns F

D qr

,which

is equivalent to Eq. 28; we have reproduced Quinn’s expression for the scalar self-

force. Notice that the second axiom eliminates the need to carry out an explicit

renormalization of the mass.

Another axiomatic approach provides an even more immediate derivation of

Quinn’s equation. This is the approach suggested by Steve Detweiler and Bernard

Whiting [2], which is based on an observation and an alternate axiom:

Detweiler–Whiting Observation The retarded ﬁeld ˚

ret

can be decomposed

uniquely into a singular piece ˚

and a regular remainder ˚

Detweiler–Whiting Axiom The singular ﬁeld produces no force on the particle.

The immediate consequence of the axiom is that only the regular ﬁeld partici-

pates in the self-force, and we once more arrive at Quinn’s equation.

The Detweiler–Whiting approach is very clean and provides a quick route to the

ﬁnal answer. The observation is not at all controversial, because the singular ﬁeld

is indeed uniquely deﬁned by the prescription outlined in Sect.6. The axiom, on the

other hand, seems too good to be true. How can it just be asserted that the singular

ﬁeld produces no force?

A fairly compelling line of argument rests on the fact that according to its deﬁ-

nition, the singular ﬁeld is strongly time-symmetric, in the sense that the ﬁeld at x

does not depend on the future nor the past of the spacetime point; it instead depends

on source points x

that are in a spacelike or lightlike relation with x.Sincewe

would expect the self-force to be sensitive to the direction of time – an advanced

ﬁeld should produce a different force from a retarded ﬁeld – it seems plausible that

the singular ﬁeld would not know whether to push or pull, and would therefore

choose to do neither.

The argument is not water-tight. For example, an alternate singular ﬁeld, deﬁned

by Dirac’s prescription

ret

adv

, would also be time-symmetric (though not

strongly time-symmetric), and could also be asserted to produce no force. The

resulting self-force, however, would be produced by

ret



adv

, and would

depend on the entire history of the particle, both past and future. We would of course

reject this candidate self-force on grounds of causality violation, but the argument

nevertheless shows that there is more to the Detweiler–Whiting singular ﬁeld than

a time-symmetry property. Another hole in the argument lies in the link between

324 E. Poisson

the time-symmetry of the singular ﬁeld and the statement that it must exert no force:

While the time-symmetry property clearly implies that the singular ﬁeld cannot pro-

duce dissipative effects on the particle, there is no reason to rule out an eventual

conservative contribution to the self-force.

The conclusion is that additional axioms are necessarily required to make sense

of the equations of motion formulated for a point particle. The axioms may seem

plausible and perhaps even self-evident, but they cannot be derived from ﬁrst prin-

ciples in the context of a classical ﬁeld theory coupled to a point particle. Such

a theory is inherently singular and ambiguous, and it necessarily requires external

input in the form of additional axioms.

10 Conclusion

Can one do better than this? The answer is “no” if we insist in treating the point

particle as a fundamental classical object. The answer, however, is “yes” if we prop-

erly understand that a point particle is merely a convenient substitute for what is

fundamentally an extended body. In this view, the length scale of the moving body

is `, not 0. The body possesses a ﬁnite density of scalar charge, the scalar ﬁeld is

ﬁnite everywhere, and its motion traces a world tube in spacetime instead of a single

world line. To determine this motion is a well-posed problem, but the description

now involves a lot of additional details. Under usual circumstances, however, ` is

much smaller than all other length scales present in the problem, such as the radius

of curvature R of the body’s trajectory. Under these circumstances the description

of the motion can be simpliﬁed so as to involve a much smaller number of vari-

ables; in the limit `=R ! 0 only the position of the center-of-mass matters, and

all couplings between the body’s multipole moments and the external ﬁeld become

irrelevant. In this limit we recover a point-particle description, with the essential

understanding that it is merely an approximate description that should not be con-

sidered to be fundamental.

To go through the details of this program is difﬁcult, and it appears that very

few authors have attempted it since the old days of Lorentz and Abraham. For a

recent discussion, and a review of this literature, see the work by Harte [6]. Another

important exception concerns the gravitational self-force acting on a small black

hole (LRR Section 5.4), which is decidedly not treated as a point mass.

It is well known that in general relativity, the motion of gravitating bodies is

determined, along with the spacetime metric, by the Einstein ﬁeld equations; the

equations of motion are not separately imposed. This observation provides a means

of deriving the gravitational self-force without having to rely on the ﬁction of a point

mass. In the powerful method of matched asymptotic expansions, the metric of the

small black hole, perturbed by the tidal gravitational ﬁeld of the external spacetime,

is matched to the metric of the external spacetime, perturbed by the black hole. The

equations of motion are then recovered by demanding that the metric be a valid

solution to the vacuum ﬁeld equations. In my opinion, this method (which was ﬁrst

Constructing the Self-Force 325

applied to the gravitational self-force problem by Mino et al. [8]) gives what is by far

the most compelling derivation of the gravitational self-force. Indeed, the method is

entirely free of conceptual and technical pitfalls – there are no singularities (except

deep inside the black hole) and only retarded ﬁelds are employed.

In this assessment I respectfully disagree with my colleague Bob Wald, who

ﬁnds that the method incorporates a number of unjustiﬁed assumptions. I would

concede that expositions of the method – including my own in LRR – might not have

sufﬁciently clariﬁed some of its subtle aspects. But I see this as faulty exposition,

not as an intrinsic difﬁculty with the method of matched asymptotic expansions.

I refer the reader to the recent work by Sam Gralla and Bob Wald [5] for their views

on this issue, and their own approach to the motion of an extended body in general

relativity.

The introduction of a point particle in a classical ﬁeld theory appears at ﬁrst sight

to be severely misguided. This is all the more true in a nonlinear theory such as

general relativity. The lesson learned here is that surprisingly often, one can get

away with it. The derivation of the gravitational self-force based on the method

of matched asymptotic expansions does indeed show that the result obtained on

the basis of a point-particle description can be reliable, in spite of all its questionable

aspects. This is a remarkable observation, and one that carries a lot of convenience:

It is indeed much easier to implement the point-mass description than to perform

the matching of two metrics in two coordinate systems. The lesson, of course, carries

over to the scalar and electromagnetic cases.

Acknowledgements I wish to thank the organizers of the school for their kind invitation to lec-

ture; Orl´eans in the summer is a very nice place to be. I wish to thank the participants for many

interesting discussions. And ﬁnally, I wish to thank Bernard Whiting for his patience. This work

was supported by the Natural Sciences and Engineering Research Council of Canada.

References

1. S. Detweiler, Class. Q. Grav. 22, S681 (2005)

2. S. Detweiler, B.F. Whiting, Phys. Rev. D 67, 024025 (2003)

3. B.S. DeWitt, R.W. Brehme, Ann. Phys. (N.Y.) 9, 220 (1960)

4. P.A.M. Dirac, Proc. R. Soc. Lond. A 167, 148 (1938)

5. S.E. Gralla, R.M. Wald, Class. Q. Grav. 25, 205009 (2008)

6. A.I. Harte, Phys. Rev. D 73, 065006 (2006)

7. J.M. Hobbs, Ann. Phys. (N.Y.) 47, 141 (1968)

8. Y. Mino, M. Sasaki, T. Tanaka, Phys. Rev. D 55, 3457 (1997)

9. E. Poisson, Living Rev. Rel. 7, URL (cited on 11 August 2010): http://www.livingreviews.org/

lrr-2004-6

10. T.C. Quinn, Phys. Rev. D 62, 064029 (2000)

11. T.C. Quinn, R.M. Wald, Phys. Rev. D 56, 3381 (1997)

12. H. Spohn, Dynamics of Charged Particles and Their Radiation Field (Cambridge University

Press, Cambridge, 2008)

13. J.L. Synge, Relativity: the General Theory (North-Holland, Amsterdam, 1960)

14. K.S. Thorne, J.B. Hartle, Phys. Rev. D 31, 1815 (1985)

15. X.H. Zhang, Phys. Rev. D 34, 991 (1986)

Computational Methods for the Self-Force

in Black Hole Spacetimes

Leor Barack

Abstract We survey the set of computational methods devised for implementing

the MiSaTaQuWa formulation in practice, for orbits around Kerr black holes. We fo-

cus on the gravitational self-force (SF) and review in detail two of these methods: (i)

the standard mode-sum method, in which the perturbation ﬁeld is decomposed into

multipole harmonics and the MiSaTaQuWa regularization is performed, effectively,

mode by mode; and (ii) m-mode regularization, whereby one regularizes individual

azimuthal modes of the full perturbation. The implementation of these strategies

involves the numerical integration of the relevant perturbation equations, and we

discuss several practical issues that arise and ways to deal with them. These issues

include the choice of gauge, the numerical representation of the particle singularity,

and the handling of high-frequency contributions near the particle in frequency-

domain calculations. As an example, we show results from an actual computation

of the gravitational SF for an eccentric geodesic orbit around a Schwarzschild black

hole, using direct numerical integration of the Lorenz-gauge perturbation equations

in the time domain.

1 Introduction and Overview

The development of a robust formulation for the self-force (SF) in curved spacetime

has been motivated strongly by the prospects of observing gravitational waves from

extreme mass-ratio inspirals (EMRIs) with LISA (see Jennrich’s contribution in this

volume). It is estimated that LISA will observe hundreds such events [53], out to

cosmological distances [52], allowing a powerful microscopy of the strong-ﬁeld

geometry outside astrophysical massive black holes. The rich science encapsulated

in the EMRI waveforms [1, 9, 10,39,54] makes this class of sources a high priority

for LISA. However, the full scientiﬁc promise of EMRI detections could only be

L. Barack (



)

School of Mathematics, University of Southampton, Southampton, SO17 1BJ,

United Kingdom

e-mail: leor@soton.ac.uk

L. Blanchet, A. Spallicci, and B. Whiting (eds.), Mass and Motion in General Relativity,

Fundamental Theories of Physics 162, DOI 10.1007/978-90-481-3015-3

12,

 Springer Science+Business Media B.V. 2011

327

328 L. Barack

realized if accurate and faithful theoretical templates of inspiral waveforms were

available by the time LISA ﬂies. The underlying idealized physical problem is that

of a structureless point particle of mass , set in a generic (eccentric, inclined)

strong-ﬁeld orbit around a Kerr black hole of a much larger mass, M .The

goal is to model the gravitational waveforms emitted as radiation reaction drives the

gradual inspiral up until the eventual plunge through the black hole’s event horizon.

A prerequisite is to calculate the local gravitational SF acting on the inspiralling

object, at least at leading order in the small mass [O.

/]. This deﬁnes the mission

statement for the ongoing “SF program” that sets the context for this review.

The theoretical framework underpinning the SF program is reviewed elsewhere

in this volume (see Wald’s, Detweiler’s, and Poisson’s contributions). It comprises

the works by Mino, Sasaki, and Tanaka [86] (gravitational SF using matched asymp-

totic expansions), Quinn and Wald [103] (gravitational SF using an axiomatic

approach), Detweiler and Whiting [44] (R-ﬁeld reinterpretation of the perturbed

motion), Gralla and Wald [57] (rigorous derivation of the SF using a one-parameter

family of spacetimes), Barack and Ori [18] (gauge dependence of the gravita-

tional SF), and Poisson [97] (a self-contained and pedagogical review, with an

elegant reproduction of previous derivations). The main end product of this theo-

retical advance was a ﬁrmly established general formula for the SF in a class of

spacetimes including Kerr. This formula (Eq. 2 below) will be the starting point of

our review. We will refer to it, following Poisson [97], as the MiSaTaQuWa formula,

an acronym based on the names of the authors of Refs. [86]and[103], where the

formula was ﬁrst derived.

Starting in the late 1990s, work began to recast the MiSaTaQuWa formula in a

practical form and implement it in actual calculations of the SF. While the “holy

grail” of this program remains the calculation of the gravitational SF for generic

orbits in Kerr, much of the initial effort has concentrated on the toy problem of the

scalar-ﬁeld SF, and on simple classes of orbits (radial, circular) in Schwarzschild

spacetime. The last few years, however, have seen ﬁrst calculations of the gravita-

tional (and electromagnetic) SFs for generic orbits in Schwarzschild – and work on

Kerr is now under way. In our presentation we shall focus, for concreteness, on the

gravitational problem.

The scope of our discussion will be restricted to work concerned with the direct

evaluation of the MiSaTaQuWa SF along a given prespeciﬁed orbit (normally taken

to be a geodesic of the background spacetime); we will not consider here the im-

portant question of how orbits evolve under the effect of the SF. There is a parallel

research effort [49,50,55,65,67,84,100,108] aimed to devise a faithful scheme for

calculations of the slow (“adiabatic”) orbital evolution in LISA-relevant sources.

This effort is largely based on a strategy proposed by Mino [81–83,107], in which

a time-average measure of the rate of change of the orbital “constants of motion” is

calculated from a certain “radiative” Green’s function without resorting to the local

SF, but neglecting its conservative effects. It is not inconceivable that this method

would prove sufﬁciently accurate for LISA applications. However, ultimately, the

performance and accuracy of this method could only be assessed against precise

calculations of the full SF.

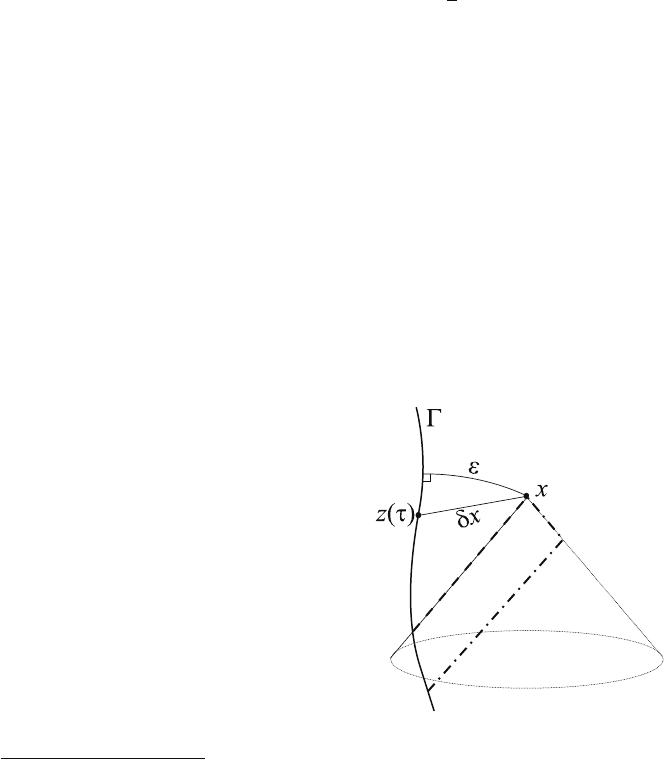
Computational Methods for the Self-Force in Black Hole Spacetimes 329

1.1 The MiSaTaQuWa Formula

The starting point for our discussion is the MiSaTaQuWa formula, which we now

state. Consider a timelike geodesic  in Kerr spacetime and let  be proper time

along  . Let also x

D z

./ describe  in some smooth coordinate system, and

 dz

=d  be the four velocity. Denote by g

˛ˇ

the Kerr background metric, and

by h

˛ˇ

the retarded metric perturbation from a particle of mass  whose worldline

is  . Assume h

˛ˇ

is given in the Lorenz gauge:

ˇ

˛ˇ I

D 0 with

˛ˇ

 h

˛ˇ



˛ˇ



: (1)

Throughout this article, and as usual in perturbation theory, indices are raised and

lowered using the background metric g

˛ˇ

, and covariant derivatives (denoted by

semicolons) are taken with respect to that metric. (We also use the conventional

geometrized units where G D c D 1, and we adopt metric signature CCC.) At

any spacetime point x the trace-reversed perturbation can be written as a sum of two

pieces,

˛ˇ

dir

˛ˇ

tail

˛ˇ

, the former being the “direct” contribution coming from

the intersection of the past light cone of x with  , and the latter being the “tail”

contribution arising from the part of  inside this light cone (see Fig. 1). Both

˛ˇ

and

dir

˛ˇ

obviously diverge when evaluated on  ;however,

tail

˛ˇ

is continuous and

differentiable (though not smooth) there.

The MiSaTaQuWa formula states that the gravitational SF along  is given by

self

.z/ D lim

x!z

k

˛ˇ  ı

tail

ˇIı

D lim

x!z



k

˛ˇ  ı

ˇIı

 k

˛ˇ  ı

dir

ˇIı



; (2)

Fig. 1 An illustration of the

setup described in the text.

z./ is a point on the timelike

worldline  (thick solid line)

and x is a ﬁeld point close

to z, shown with a portion

of its past light cone.  is the

spatial geodesic distance from

x to  and ıx

 x

z

The metric perturbation at x

consists of a direct and a tail

contribution, illustrated

by the thick dashed and

dash-dot lines, respectively

In the original MiSaTaQuWa formulation, the SF is not expressed directly in terms of the gradient

tail

˛ˇ

, but rather as a worldline integral over the gradient of the relevant retarded Green’s func-

tion (cf. Eq. 1.9.6 of Poisson [97]). The commutation of the derivative operator and the worldline

integral produces local terms at x, which, however, vanish (in the vacuum case which concerns us

here) upon contraction with k

˛ˇ ı

at the limit x ! z.

330 L. Barack

where k

˛ˇ  ı

.x/ isanysmoothoff- extension of the tensor k

˛ˇ  ı

deﬁned on  as

˛ˇ  ı

˛ı



 g

˛ˇ







ˇ

˛ı

ˇ

: (3)

An alternative formulation, as compelling in its interpretation of the perturbed

motion as it is useful for practical implementation, is due to Detweiler and Whiting

[40, 44]. This formulation introduces the alternative splitting

˛ˇ

where the “R” ﬁeld (unlike the tail ﬁeld) is a certain smooth solution of the pertur-

bation equations, which, nonetheless, gives rise to the same physical SF as the tail

ﬁeld:

self

.z/ D lim

x!z

k

˛ˇ  ı

ˇIı

D lim

x!z



k

˛ˇ  ı

ˇIı

 k

˛ˇ  ı

ˇIı



: (4)

The gradient ﬁelds

˛ˇ I

and

tail

˛ˇ I

differ by terms which are continuous (yet

not differentiable) on  (cf. Eq. 1.9.5 of [97]), and which vanish at x ! z upon

contraction with k

˛ˇ  ı

. The singular “S” ﬁeld

˛ˇ

and the direct ﬁeld

dir

˛ˇ

the same leading-order singularity near  . More precisely, considering a particular

point z on  and a nearby off- ﬁeld point x (see Fig. 1), we have [21, 87,91]

S;dir

˛ˇ

.x/ D

4 Ou

.x/Ou

.x/

.x/

 w

S;dir

˛ˇ

.x/

.x/

C c

S;dir

˛ˇ

; (5)

where Ou

is the four-velocity vector parallelly propagated from z to x,  is the spatial

geodesic distance from x to  (i.e., the length of the short normal geodesic section

connecting x to  ), w

S;dir

˛ˇ

are smooth functions of x (and z) which vanish at x ! z

at least quadratically in the coordinate differences x

 z

,andc

S;dir

˛ˇ

are constants.

The S and direct ﬁelds differ only in the explicit form of w

˛ˇ

and (possibly) in the

value of c, neither of which will be important in what follows.

Equations 2 and 4 prescribe the correct regularization of the gravitational SF

and form the fundamental basis for all SF calculations. It is important to make the

point that the calculation methods to be described below do not involve any fur-

ther regularization: they are simply implementations of the MiSaTaQuWa formula.

In particular, the mode-sum methods at the focus of our discussion (sometimes

referred to, perhaps misleadingly, as “regularization” methods) simply recast the

MiSaTaQuWa formula in a more practical – but otherwise equivalent – form.

1.2 Gauge Dependence

Another crucial point to have in mind is that the MiSaTaQuWa formula (2) is guar-

anteed to hold true only if

˛ˇ

satisﬁes the Lorenz-gauge condition (1). Relatedly,

The quantity k

˛ˇ ı

ˇIı

is the linear perturbation in the connection coefﬁcients, ı

ˇ



projected orthogonally to  ;thatis,k

˛ˇ ı

ˇIı

D .g

ˇ



/ı

ˇ