Blanchet L., Spallicci A., Whiting B. (Eds.) Mass and Motion in General Relativity

Подождите немного. Документ загружается.

Computational Methods for the Self-Force in Black Hole Spacetimes 351

SF calculations we need not only 

but also its derivatives. Since, for example,



lm;r

is a discontinuous function of t, we will inevitably face here the well known

“Gibbs phenomenon”: the Fourier sum will fail to converge to the correct value

at r ! r

.t/. Of course, the problematic behavior of the Fourier sum is simply a

consequence of our attempt to reconstruct a discontinuous function as a sum over

smooth harmonics.

From a practical point of view this would mean that (i) at the coincidence limit

r ! r

.t/ the sum over ! modes would fail to yield the correct one-sided values

of 

lm;r

,howevermany! modes are included in the sum; and (ii) if we reconstruct



lm;r

at a point r Dr

off the worldline, then the Fourier series should indeed for-

mally converge, however the number of ! modes required for achieving a prescribed

precision would grow unboundedly as r

approaches r

.t/, making it extremely dif-

ﬁcult to evaluate 

lm;r

at the coincidence limit.

This technical difﬁculty is rather generic, and will show also in calculations of

the local EM and gravitational ﬁelds. The situation is no different in the Kerr case,

because there too the mode-sum formula requires as input the spherical-harmonic

modes of the perturbation ﬁeld, and for each such mode the source is represented

by a ı-distribution on a thin shell, which renders the ﬁeld derivatives discontinuous

across that shell. The problem takes an even more severe form when considering EM

or gravitational perturbations via the Teukolsky formalism: Here, the l;m modes of

the perturbation ﬁelds (now the Newman–Penrose scalars) are not even continuous

at the particle’s orbit – a consequence of the fact that the source term for Teukolsky’s

equation involves derivatives of the electric four-current or the energy–momentum

tensor (a single derivative in the EM case; a second derivative in the gravitational

case). Again, a naive attempt to construct these multipoles as a sum over their !

modes will be hampered by the Gibbs phenomenon.

A simple and elegant way around the problem was proposed recently in Ref. [23].

It was shown how the desired values of the ﬁeld and its derivatives at the particle can

be constructed from a sum over properly weighted homogeneous(source-free) radial

functions R

lm!

.r/, instead of the actual inhomogeneous solutions of the frequency-

domain equation. The Fourier sum of such homogeneous radial functions, which are

smooth everywhere, converges exponentially fast. The Fourier sum of the deriva-

tives, which are also smooth, is likewise exponentially convergent. The validity of

the method (and the exponential convergence) was demonstrated in Ref. [23] with

an explicit numerical calculation in the scalar-ﬁeld monopole case (l D 0). It was

later implemented in a frequency-domain calculation of the monopole and dipole

modes of the Lorenz gauge metric perturbation for eccentric orbits in Schwarzschild

[13, 25, 26]. The same method should be applicable for any of the other problems

mentioned above, including the calculation of EM and gravitational perturbations

using Teukolsky’s equation.

The method of Ref. [23] (dubbed method of extended homogeneous solutions)

completely circumvents the problem of slow convergence (or the lack thereof) in

frequency-domain calculations involving point sources. It makes the frequency-

domain approach an attractive method of choice for SF calculations. The method

is now being implemented in ﬁrst calculations of the scalar-ﬁeld SF for Kerr or-

bits [119].

352 L. Barack

4 An Example: Gravitational Self-Force in Schwarzschild Via

1C1D Evolution in Lorenz Gauge

As an example of a fully worked out calculation of the SF, we review here the work

by Barack and Sago on eccentric geodesic in Schwarzschild [24, 26]. This work

represents a direct implementation of the mode-sum formula in its original form

(20). The decomposed Lorenz-gauge metric perturbation equations are integrated

directly using numerical evolution in 1C1D. The numerical algorithm employs a

straightforward fourth-order-convergent ﬁnite-difference scheme (using a version

of the Lousto–Price method) on a staggered numerical mesh based on characteris-

tic coordinates. Below we brieﬂy describe the perturbation formalism, discuss the

numerical implementation in some more detail, and present some results.

4.1 Lorenz-Gauge Formulation

The linearized Einstein equation in the Lorenz gauge takes the form



˛ˇ

C 2R







D16T

˛ˇ

; (43)

where



is the trace-reversed metric perturbation (Eq. 1),  is the covari-

ant D’Alembertian operator, R

˛ˇ  ı

is the Riemann tensor of the background

spacetime, and T

˛ˇ

in the source’s energy–momentum tensor. For a point par-

ticle of mass  moving on a timelike geodesic x



./, the latter is modeled as

˛ˇ



/ D 

1

.g/

1=2

Œx



 x



./u

d; (44)

where g is the background metric’s determinant and u

in the particle’s four-

velocity. Eq. 43 is a linear, diagonal hyperbolic system, which admits a well-posed

initial-value formulation on a spacelike Cauchy hypersurface (see, e.g., Theorem

10.1.2 of [118]). Furthermore, if the gauge conditions (Eq. 1) are satisﬁed on the

initial Cauchy surface, then they are guaranteed to hold everywhere (assuming that

Eq. 43 is satisﬁed everywhere and that T

˛ˇ

Iˇ

D 0, as in our case).

We now specialize to eccentric geodesics around a Schwarzschild black hole,

and employ a Schwarzschild coordinate system (t;r;;') in which the orbit is

equatorial (

D =2). Such orbits constitute a two-parameter family; we may

characterize each orbit by the radial “turning points” r

min

and r

max

, or alterna-

tively by the “semi-latus rectum” p  2.r

max

min

/=.r

max

C r

min

/ and “eccentricity”

e  .r

max

 r

min

/=.r

max

C r

min

The gauge conditions (1) do not fully specify the gauge: There is a residual gauge freedom within

the family of Lorenz gauges, h

˛ˇ

! h

˛ˇ

C 

˛Iˇ

C 

ˇI˛

, with any 



satisfying 



D 0.Itis

easy to verify that both Eqs. 1 and 43 remain invariant under such gauge transformations.

Computational Methods for the Self-Force in Black Hole Spacetimes 353

Barack and Lousto [15] decomposed the metric perturbation into tensor

harmonics, in the form

˛ˇ



l;m

iD1

.i/lm

.r; t / Y

.i/lm

˛ˇ

.; '/; (45)

and similarly for the source T

˛ˇ

. The harmonics Y

.i/lm

˛ˇ

.; '/ (whose components

are constructed from ordinary spherical harmonics and their ﬁrst and second deriva-

tives) form a complete orthogonal basis for second-rank covariant tensors on a

2-sphere (see Appendix A of [15]). The time-radial functions

.i/lm

(i D 1;:::;10)

form our basic set of perturbation ﬁelds, and serve as variables for the numerical

evolution.

The tensor-harmonic decomposition decouples Eq. 43 with respect to

l;m, although not with respect to i: For each l;m,thevariables

.i/lm

satisfy a cou-

pled set of hyperbolic (in a 1+1D sense) scalar-like equations, which may be written

in the form



.2/

.i/lm

C M

.i/l

.j /

.j /lm

D S

.i/lm

.i D 1; : : : ; 10/: (46)

Here 

.2/

is the 1+1D scalar ﬁeld wave operator @

C V.r/,wherev and u are the

standard Eddington–Finkelsteinnull coordinates, and V.r/D

.12M=r/



2M=r

Cl.l C 1/=r



is an effective potential. The “coupling” terms M

.i/l

.j /

.j /lm

involve

ﬁrst derivatives of the

.j /lm

’s at most (no second derivatives), so that, conveniently,

the set (46) decouples at its principal part. The decoupled source terms S

.i/lm

are

each / ıŒr  r

./ (no derivatives of ı function) and, as a result, the physical

solutions

.j /lm

are continuous even at the particle. Explicit expressions for the

coupling terms and the source terms in Eq. 46 can be found in Ref. [15].

In addition to the evolution equations (46), the functions

.i/lm

also satisfy

four ﬁrst-order elliptic equations, which arise from the separation of the gauge

conditions (1)intol;m modes. In the continuum initial-value problem, the solu-

tions

.i/lm

satisfy these “constraints” automatically if only they satisfy them on

the initial Cauchy surface. This is more difﬁcult to guarantee in a ﬁnite-difference

treatment, where (i) it is often impossible to prescribe exact initial data that satisfy

the constraints, and (ii) discretization errors may amplify constraint violations over

the evolution. Inspired by a remedy proposed for a similar problem in the context

of nonlinear Numerical Relativity [58], Ref. [15] proposed the inclusion of “diver-

gence dissipation” terms, / h

Iˇ

˛ˇ

, in the original set (43), so designed to guarantee

that any violations of the Lorenz-gauge conditions are efﬁciently damped during

the evolution. These damping terms modify only the explicit form of the M terms

in Eq. 46 as shown in [15].

To simplify the appearance of Eq. 45 we have used here a slightly different normalization than

that of [15] for the functions

.i/lm

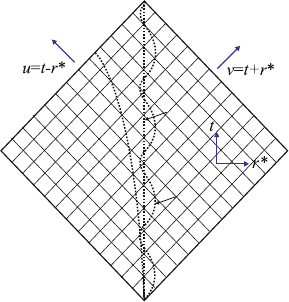
354 L. Barack

4.2 Numerical Implementation

The code developed by Barack and Sago [24, 26] solves the coupled set (46)

(with constraint dissipation terms incorporated in the M terms) via time evolution.

The numerical domain, covering a portion of the external Schwarzschild geome-

try, is depicted in Fig. 3. The numerical grid is based on Eddington–Finkelstein

null coordinates v; u, and initial data (the values of the 10 ﬁelds

.i/lm

for each

l;m) are speciﬁed on two characteristic initial surfaces v D const and u D const.

Equations 46 are then discretized on this grid using a ﬁnite-difference algorithm

which is globally fourth-order convergent. The numerical integrator solves for the

various

.i/lm

’s along consecutive v D const rays. A particularly convenient fea-

ture of this setup is that no boundary conditions need be speciﬁed (the characteristic

grid has no causal boundaries). Moreover, one need not be at all concerned with

the determination of faithful initial conditions: It is sufﬁcient to set

.i/lm

D 0 on

the initial surfaces and simply let the resulting spurious radiation (which emanate

from the intersection of the particle’s worldline with the initial surface) dissipate

away over the evolution time. The early part of the evolution, which is typically

dominated by such spurious radiation, is simply discarded.

The conservative modes l D0 and l D1 (the monopole and dipole, respectively)

require a separate treatment, as they do not evolve stably using the above numeri-

cal scheme. (A naive attempt to evolve these modes leads to numerical instabilities

which, so far, could not be cured.) Fortunately, the set (46) simpliﬁes considerably

for these modes, and solutions can be obtained in a semi-analytic manner based

on physical considerations. Detweiler and Poisson [43] worked out the l D0; 1

Lorenz-gauge solutions for circular orbits, and their work is generalized to eccentric

orbits in Ref. [13], relying on the aforementioned method of extended homogeneous

solutions. The calculation of [13] yields the values of the ﬁelds

.i/lm

and their

derivatives for l D0; 1.

“Event

Horizon”

Initial surface

“Null

Infinity”

Initial surface

Plunge

Circular

Eccentric

Fig. 3 The numerical 1C1D domain in the Barack–Sago code [24, 26]: A staggered mesh

based on characteristic (Eddington–Finkelstein) coordinates v; u. t and r



are, respectively, the

Schwarzschild time and tortoise radial coordinates. The evolution proceeds from characteristic ini-

tial data on two null surfaces. Illustrated are a few sample geodesic orbits (radial plunge, circular,

eccentric)

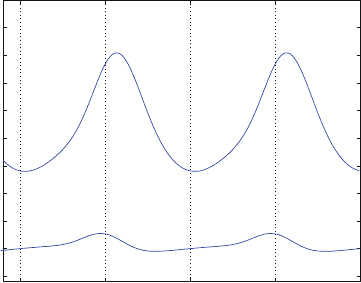
Computational Methods for the Self-Force in Black Hole Spacetimes 355

−0.5 0 0.5 1 1.5

−0.005

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0.04

0.045

Radial phase / (2π)

p = 7.0 M

e = 0.2

Fig. 4 The gravitational SF [in units of .=M /

] along a Schwarzschild geodesic with semi-latus

rectum p D 7M and eccentricity e D 0:2. The upper and lower graphs show F

self

and F

self

respectively. Integer values on the horizontal axis correspond to periapses (r D r

min

)

To construct the l modes F

˛l

[the necessary input for the mode-sum formula

(20)], one ﬁrst substitutes the expansion (45) in the expression for the full force F

(left-hand expression in Eq. 9), and then formally expands the result in spherical

harmonics. The outcome is a formula for F

˛l

given in terms of the various ﬁelds

.i/l

and their derivatives (evaluated at the particle and summed over m), where, if

the ﬁxed-k extension is used, one ﬁnds in general l 3  l

 l C3. One then uses

the numerical values of the ﬁelds

.i/lm

and their derivatives, as calculated along

the orbit using the above code, to construct F

˛l

for sufﬁciently many l modes. The

mode-sum formula (20) then gives the SF. Figure 4 shows the ﬁnal result for an

eccentric geodesic with p D 7M and e D 0:2.

The calculation we have just described represents a milestone in the SF program:

We now ﬁnally have a code capable of tackling the generic EMRI-relevant SF prob-

lem in Schwarzschild. (Indeed, to address the fully generic physical problem would

require a ﬁnal generalization to the Kerr case!) Using this code, and similar codes

developed independently by others [42], we can now begin to explore the physical

consequences of the gravitational SF – particularly those effects associated with its

conservative piece. Work done so far includes (i) study of gauge invariant SF effects

on circular orbits [42], (ii) comparison of SF calculations and results from PN the-

ory in the weak ﬁeld regime [42,109], (iii) comparison of SF results from different

calculation schemes and using different gauges [109], and (iv) a calculation of the

shift in the last stable circular orbit (and its frequency) due to the conservative piece

of the SF [25]. Work is in progress to calculate SF-related precessional effects for

eccentric orbits.

356 L. Barack

5 Toward Self-Force Calculations in Kerr: the Puncture

Method and m-Mode Regularization

The time-domain Lorenz-gauge treatment of Section 4 relies crucially on the separa-

bility of the ﬁeld equations into (tensorial) spherical harmonics, which is no longer

possible in Kerr. In the Kerr problem one can at best separate the metric perturbation

equations into azimuthal m modes, using the substitution

˛ˇ

mD1

˛ˇ

.t;r;/e

im'

: (47)

Then one faces solving the coupled set for the 2C1D variables

˛ˇ

. This, nowadays,

is easily within the capability of even a standard desktop computer; indeed, over the

past decade, 2C1D numerical evolution has been a method of choice in many studies

of Kerr perturbations [11, 71–74,77,95,112]. Alas, the introduction of a ı-function

source in a 2C1D evolution is problematic, since the variables

˛ˇ

then suffer a

singularity near the particle. The puncture method, which we have mentioned brieﬂy

in Section 3.2, overcomes this technical difﬁculty. In this section we review this

method (as implemented by Barack and Golbourn [11]) in some more detail. We

also describe a new, ad hoc, regularization method – the m-mode regularization

scheme – which enables a straightforward construction of the SF directly from the

2C1D numerical solutions, without resorting to a multipole decomposition.

5.1 Puncture Method in 2C1D

In Section 1 we have split the (trace-reversed) metric perturbation as

˛ˇ

, with the gravitational SF then obtained from the smooth ﬁeld

˛ˇ

as prescribed

in Eq. 4. Here we introduce a new splitting,

˛ˇ

punc

˛ˇ

res

˛ˇ

; (48)

so that

˛ˇ

res

˛ˇ

C .

punc

˛ˇ



˛ˇ

/: (49)

We denote the m modes of these various quantities, deﬁned as in Eq. 47,by

R;m

˛ˇ

res;m

˛ˇ

, etc. The new splitting is deﬁned (in a nonunique way) by devising a puncture

A full separation of variables in Kerr is possible within Teukolsky’s formalism, which, alas, brings

about the metric reconstruction and gauge-related difﬁculties discussed in previous chapters. A full

separation of the metric perturbation equations themselves, in Kerr, has not been formulated yet,

to the best of our knowledge.

Computational Methods for the Self-Force in Black Hole Spacetimes 357

ﬁeld

punc

˛ˇ

, given analytically, which approximates

˛ˇ

near the particle well enough

that the m modes of the resulting residual ﬁeld

res

˛ˇ

are continuous and differentiable

along the particle’s worldline (and anywhere else). A particular such puncture is pre-

scribed below (Eq. 56). The form of the puncture function away from the particle can

be chosen as convenient; for example, in such a way that it can be decomposed into

m modes explicitly, in analytic form (as in Ref. [11], for a scalar-ﬁeld toy model).

The Lorenz-gauge perturbation equations (43) are now written in the form



res

˛ˇ

C 2R





res



D S

res

˛ˇ

; (50)

with

res

˛ˇ

16T

˛ˇ

 

punc

˛ˇ

 2R





punc



: (51)

The support of the source S

res

˛ˇ

now extends beyond the particle’s worldline, but it

contains no ı function on the worldline.

The equations are separated into m modes,

with the m-mode source given by

res;m

˛ˇ

.t;r;/

2





res

˛ˇ

.t;r;;'/e

im'

d': (52)

If the puncture is sufﬁciently simple, the source S

res;m

˛ˇ

can be evaluated in closed

form (as in [11]). The m-mode ﬁeld equations for the variables

res;m

˛ˇ

.t;r;/,which

are everywhere continuous and differentiable, can now be integrated numerically

using straightforward ﬁnite differentiation on a 2C1D grid.

To ease the imposition of boundary conditions for

res;m

˛ˇ

, it is convenient to sup-

press the support of the puncture

punc

˛ˇ

away from the particle, so that the physical

boundary conditions for

res

˛ˇ

become practically identical to that of the full re-

tarded ﬁeld

˛ˇ

.In[11] this is achieved in a simple way by introducing an auxiliary

“worldtube” around the particle’s worldline (in the 2C1D space): Inside this world-

tube one solves the “punctured” m-mode equations for

res;m

˛ˇ

, while outside the

worldtube one uses the original, retarded-ﬁeld m-modes

˛ˇ

as evolution variables;

the value of the evolution variables is adjusted on the boundary of the worldtube

using

˛ˇ

res;m

˛ˇ

punc;m

˛ˇ

Two very similar variants of the puncture scheme have been developed and im-

plemented independently by two groups [11,77] – both for the toy model of a scalar

charge on a circular orbit around a Schwarzschild black hole (refraining from a

spherical harmonics decomposition and instead working in 2C1D). The method is

yet to be applied to Kerr and to gravitational perturbations.

This can be shown by integrating S

res

˛ˇ

over a small 3-ball containing the particle (at a given time),

and then inspecting the limit as the radius of the ball tends to zero [11].

358 L. Barack

5.2 m-Mode Regularization

The 2C1D numerical solutions obtained using the puncture method can be used

to construct the input modes F

˛l

for the mode-sum formula (20), but this would

require the additional step of a decomposition in spherical harmonics. It appears,

however, that there is a simple way to construct the SF directly from the residual

modes

res;m

˛ˇ

, without resorting to a multipole decomposition. Such “m-mode reg-

ularization” procedure was prescribed recently in Ref. [12] for the scalar, EM, and

gravitational SFs. We describe it here as applied to the gravitational SF.

In analogy with Eq. 9, let us deﬁne the “force” ﬁelds

res

.x/ D k

˛ˇ  ı

res

ˇIı

punc

.x/ D k

˛ˇ  ı

punc

ˇIı

: (53)

Then, recalling Eqs. 4 and 49, we may write the SF at a point z along the orbit as

self

.z/ D lim

x!z

res

.x/ C



punc

.x/  F

.x/

i

: (54)

Recall that the expression in square brackets (D k

˛ˇ  ı

ˇIı

) is a smooth (ana-

lytic) function of x, and so the limit x ! z is well deﬁned.

Now consider a particular puncture function, prescribed as follows. For an arbi-

trary spacetime point x outside the black hole, let ˙

be the spatial hypersurface t D

const containing x,letN.t/ be the value of  at which ˙

intersects the particle’s

worldline, and denote Nz.t/  zŒN.t/ and Nu

 u

.Nz/. For given x deﬁne the coordi-

nate distance ıx

 x

Nz

.t/ [with Boyer–Lindquist components .0;ır;ı;ı'/],

and construct the three quantities

,andı Nu

deﬁned just as S

, S

,andıu

Eqs. 23–25, with z replaced by Nz.Forjıxjvery small,thesum

approximates

the squared geodesic distance from x to the worldline, and Nu

.z/Cı Nu

approximates

the four-velocity Ou

parallelly propagated from Nz to x:

D 

C O.ıx

/; Nu

C ı Nu

DOu

C O.ıx

/ (55)

(recall Eq. 22). We emphasize, however, that here the quantities

,andı Nu

are given globally, in closed form, for any x outside the black hole. The puncture

function we wish to consider is given, for any x,by

punc

˛ˇ

.x/ D

4



C ı Nu

CNu

ı Nu



1=2

: (56)

This function can be attenuated far from the particle in order to control its global

properties, but such modiﬁcations will not affect our discussion here.

We now recall the form of the “physical” singular ﬁeld

˛ˇ

expressed in Eq. 5.

This expression applies to any nearby points z and x, but here we wish to apply it

with x being a given point near the worldline and z DNz.t/ being the associated

Computational Methods for the Self-Force in Black Hole Spacetimes 359

worldline point on ˙

. It is not difﬁcult to show [12] that, near the particle, the

difference between the puncture (56) and the S ﬁeld has the form

punc

˛ˇ



˛ˇ

DN

3

.4/

˛ˇ

.ıx/ C const C O.ıx

/; (57)

where N



1=2

,andP

.4/

˛ˇ

is a smooth function of the coordinate differences ıx

of homogeneous order .ıx/

. It follows that the difference between the correspond-

ing force ﬁelds has the local form

punc

.x/  F

.x/ DN

5

.5/

.ıx/ C O.ıx/ (58)

(for any smooth k-extension), where P

.5/

is yet another smooth function, now of

homogeneous order .ıx/

. Notice that F

punc

F

is bounded but generally discon-

tinuous (direction dependent) at x !Nz.FromEq.54 it then follows that F

res

too

is bounded but discontinuous at x !Nz [since the limit of the entire expression in

square brackets in (54) is known to be deﬁnite].

We now arrive at the crucial step of our discussion. In Eq. 54, for a given point z

along the particle’s worldline, we express the (analytic) function in square brackets

as a formal sum over m modes, in the form

self

.z/ D lim

x!z

mD1

˛;m

res

.x/ C



˛;m

punc

.x/  F

˛;m

.x/

i

; (59)

where

˛;m

res

.x/ 

2





res

.t;r; '

INz/e

im.''

; (60)

and similarly for F

˛;m

punc

and F

˛;m

. Since the m-mode sum is formally a Fourier

expansion, and since the Fourier expansion of an analytic function converges uni-

formly, we may replace the order of limit and summation in Eq. 59:

self

.z/ D

mD1

lim

x!z

˛;m

res

.x/ C



˛;m

punc

.x/  F

˛;m

.x/

i

: (61)

From Eq. 58, omitting the terms O.ıx/ as they cannot possibly affect the ﬁnal value

of the SF in Eq. 54,wehave

lim

x!z



˛;m

punc

 F

˛;m



D lim

x!Nz

2

im'





N

5

.5/

im'

; (62)

where the integrand is evaluated at ' D '

and where we have used the fact that

x ! z implies also x !Nz. Crucially, one ﬁnds [12] that the last integral vanishes at

360 L. Barack

the limit x !Nz,foranym, regardless of the explicit form of P

.5/

Hence, Eq. 61

reduces to

self

.z/ D

mD1

˛;m

res

.z/: (63)

Here the substitution x D z is allowed since the limit x ! z is known to be well

deﬁned (and, in particular, direction independent). Phrased differently, the modes

˛;m

res

corresponding to our puncture (56) are continuous at the particle, as desired.

Our result (63) can be written explicitly in terms of the m modes of the residual

ﬁeld

res

ˇ

, and easily so if we use the ﬁxed-k extension introduced in Section 2.3

(the choice of k-extension may affect the value of the individual m modes, but not

the eventual value of the SF). We then have

self

mD1

k

˛ˇ  ı



res;m

ˇ

im'



Iı

; (64)

where, of course, the derivatives are evaluated at the particle.

Equation 64 prescribes an extremely simple algorithm for constructing the SF

in a 2C1D framework. In the puncture scheme we effectively “regularize” the ﬁeld

equations themselves (not their solutions, as in the standard l-mode regularization

method), by writing them in the form (50) with a sufﬁciently accurate puncture func-

tion (like the one prescribed in 56). Once the m modes of the residual perturbation

have been solved for, the SF is constructed directly from these mode with no further

regularization needed.

The m-mode method is yet to be applied in actual calculations of the SF. It has

the potential of providing a robust, simple, and efﬁcient framework for calculations

of the gravitational SF in Kerr spacetime.

6 Reﬂections and Prospects

We have attempted here to give a snapshot of the activity surrounding the devel-

opment of reliable, efﬁcient, and accurate computational methods for the SF in

black hole spacetimes. The problem still attracts considerable attention (more than

half of the papers on our reference list date 2005), with a multitude of differ-

ent approaches being studied by different groups. This multitude is, of course, a

great blessing, as it offers the opportunity for cross-validation of techniques and

It should not come as a surprise that at x D z the sum over m-modes F

˛;m

punc

F

˛;m

(which are all

zero) fails to recover the original function F

punc

F

(which is discontinuous and hence indeﬁnite).

Recall that the formal Fourier sum at a step discontinuity (where the function itself is indeﬁnite) is

in fact convergent: it yields the two-side average value of the function at the discontinuity. Techni-

cally, this peculiarity of the formal Fourier expansion is due simply to the noninterchangeability of

the sum and limit at the point of discontinuity.