Blanchet L., Spallicci A., Whiting B. (Eds.) Mass and Motion in General Relativity
Подождите немного. Документ загружается.


Radiation Reaction and Energy–Momentum Conservation 371
where DP D .ac/ 1: The retarded field strength will read:
F
ret
D
e..ac/ 1/
2
v
Œ
c
e
a
Œ
c
; (8)
where antisymmetrization is defined by e.g. v
Œ
c
D v
c
v
c
. The retarded po-
tential in Minkowski space admits a natural decomposition with respect to T-parity:
A
ret
D A
self
C A
rad
; (9)
where the radiative part A
rad
D
1
2
A
ret
A
adv
obeys an homogeneous wave equa-
tion, while the self part A
self
D
1
2
A
ret
C A
adv
has a source at x D z.s/. One could
expect that only T-symmetric A
self
corresponds to the bound field, but it is not so.
For an accelerated charge the situation is more subtle.
2.1 Decomposition of the Stress Tensor
Constructing the energy–momentum tensor
F
T
with the retarded field F
ret
, one
finds that it admits a natural decomposition:
F
T
D
F
T
emit
C
F
T
bound
; (10)
where the first term is selected by its dependence on as
2
:
F
T
emit
D
..ac/
2
C a
2
/c
c
2
; (11)
while the second contains higher powers of
1
:
F
T
bound
D
a
.
c
/
C 2.ac/c
c
.ac/v
.
c
/
3
C
v
.
c
/
c
c
2
4
; (12)
where symmetrization without 1=2 is understood, say v
.
c
/
D v
c
C v
c
.The
“emit” part (11) has the following properties:
It is the tensor product of two null vectors c
.
It is traceless.
It falls off as jxj
2
when jxj!1.
As follows from the differentiation rules (7), it is divergence free without assum-
ing the validity of the equations of motion:
@
F
T
emit
D 0: (13)
All these features indicate that T
emit
describes the outgoing radiation.

372 D. Gal’tsov
Since the total energy–momentum tensor including the contribution of charges is
(on shell) divergence free, with account for (13)wefindthat
@
F
T
bound
C @
m
T
D 0; (14)
so the bound field momentum can be exchanged with the particle momentum. Note,
that outside the world line the bound stress tensor is divergence free. It is also worth
noting, that Eq. 13 does not mean that there is no reaction force acting on a particle
that counterbalances the emitted momentum.
Consider now the total balance of forces. The conservation of the total four-
momentum (2) implies that the sum of the mechanical momentum and the momen-
tum carried by the electromagnetic field is constant (for simplicity we do not include
the external field):
dp
mech
ds
C
dp
em
ds
D 0: (15)
Here the mechanical part is proportional to the bare mass of the charge
p
mech
D
Z
m
T
d˙
D m
0
v
; (16)
while the field part is given by
p
em
D
Z
F
T
d˙
; (17)
where integration of the electromagnetic stress tensor is performed over a space-like
hypersurface whose choice will be specified later on. It has to be emphasized that
the stress tensor of the electromagnetic field is constructed in terms of the physical
retarded field. According to the above splitting, we can write
dp
mech
ds
D f
emit
C f
bound
; (18)
f
emit
D
Z
F
T
emit
d˙
;f
bound
D
Z
F
T
bound
d˙
: (19)
On the other hand, the derivative of the bare mechanical momentum of the charge
can be found by substituting the retarded field into the equation of motion. In this
case it is useful to decompose the retarded field according to (9), obtaining another
split of the mechanical momentum:
dp
mech
ds
D eF
ret
v
D e
F
self
C F
rad
v
D f
self
C f
rad
: (20)

Radiation Reaction and Energy–Momentum Conservation 373
Now, somewhat unexpectedly, f
rad
¤ f
emit
and f
self
¤ f
bound
, the difference
being called the Schott term [11]:
f
rad
D f
emit
C f
Schott
;f
self
D f
bound
f
Schott
: (21)
Clearly,
f
self
C f
rad
D f
bound
C f
emit
; (22)
as expected. Note that both f
bound
and f
self
contain divergences that mutually cancel
in Eq. 22.
The forces f
self
and f
rad
can be found using the Green functions [17]
G
self
.Z/ D ı.Z
2
/; G
rad
.Z/ D
Z
0
jZ
0
j
ı.Z
2
/; (23)
where Z
D Z
.s; s
0
/ D z
.s/ z
0
.s
0
/. Substituting the value of the electromag-
netic field generated by the charge on its world line one obtains
f
.s/ D 2e
2
Z
Z
Œ
.s; s
0
/v
.s
0
/v
.s/
d
dZ
2
G.Z/ds
0
; (24)
for both f
self
and f
rad
. Due to delta-functions, only a finite number of Taylor expan-
sion terms in D s s
0
contribute to the integral. In the four-dimensional case, it
is sufficient to retain the terms up to
3
:
2Z
Œ
.s; s
0
/v
.s
0
/v
.s/ DPv
2
2
3
.Rv
C v
Pv
2
/
3
C O.
4
/: (25)
Taking into account that Z
2
D
2
C O.
4
/, the leading terms in the expansions of
derivatives of the Green functions will be
d
dZ
2
G
self
.Z/ D
d
d
2
ı.
2
/;
d
dZ
2
G
rad
.Z/ D
d
d
2
jj
ı.
2
/
: (26)
Regularizing the delta-functions of
2
by point-splitting
ı.
2
/ D lim
"!C0
ı.
2
"
2
/ D lim
"!C0
ı. "/ C ı. C "/
2"
; (27)
with a prescription that the limit should be taken after evaluating the integrals, one
finds
f
self
D
e
2
2"
a
;f
rad
D
2e
2
3
.v
a
2
CPa
/: (28)
After the mass renormalization, m
0
C
1
2"
D m, we get the Lorentz–Dirac equation
ma
D
2e
2
3
.v
a
2
CPa
/: (29)

374 D. Gal’tsov
The first term at the right-hand side is equal to the derivative of the momentum
carried away by radiation,
f
emit
D
dp
emit
ds
D
2e
2
3
a
2
v
: (30)
Its independent evaluation by integration of
F
T
emit
can be found in [11]. The sec-
ond total derivative term is the Schott term. It is worth noting, that within the local
calculation, the Schott term originates from the T-odd part of the retarded field.
2.2 Bound Momentum
An explicit evaluation of the bound momentum associated with a given moment of
proper time s on the particle world-line,
p
bound
.s/ D
Z
˙.s/
F
T
bound
d˙
; (31)
was given in [11], which we follow here. First of all one has to choose the space-like
hypersurface ˙.s/ intersecting the world line at x
D z
.s/. A convenient choice
will be the hyperplane orthogonal to the world line
v
.s/ .x
z
.s// D 0: (32)
The integral (31) is divergent on the world line. We introduce the small length
parameter ", the radius of the 2-sphere @Y
"
.s/ (Fig. 1), defined as the intersection of
the hyperplane (32) with the hyperboloid .x z.s//
2
D"
2
. We also introduce the
sphere @Y
R
.s/ of the large radius R defined as the intersection of ˙.s/ with the
hyperboloid .x z.s//
2
DR
2
. The total field momentum can be obtained as
the limit " ! 0; R !1of the integral over the domain Y.s/ ˙.s/ between the
boundaries @Y
"
.s/ and @Y
R
.s/.
Let us evaluate the variation of this quantity between the instants s
1
and s
2
of the
proper time on the world line of the charge
p
em
D
Z
Y.s
2
/
T
d˙
Z
Y.s
1
/
T
d˙
: (33)
For the bound momentum it is convenient to consider the tubes S
"
and S
R
formed
as sequences of the spheres @Y
"
.s/ and @Y
R
.s/ on the interval s 2 Œs
1
;s
2
and to
transform this quantity to
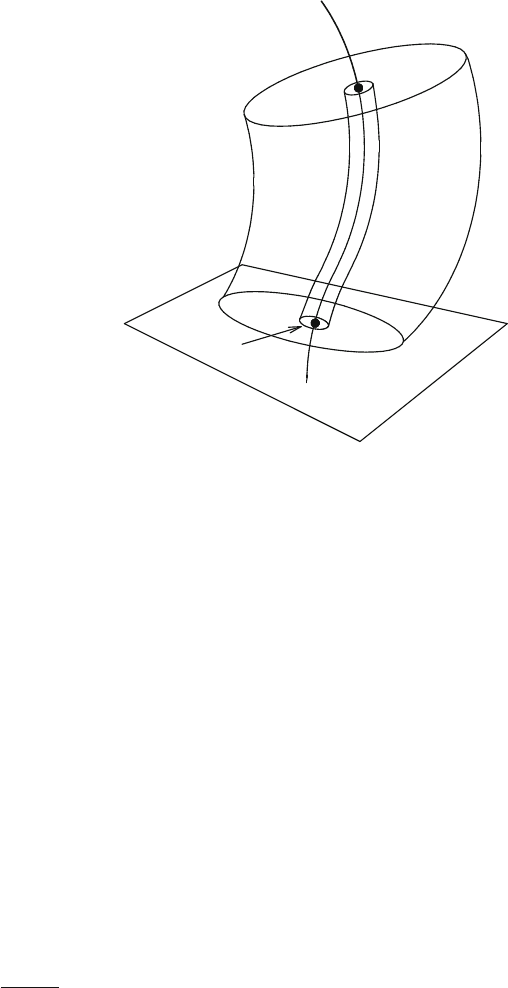
Radiation Reaction and Energy–Momentum Conservation 375
Fig. 1 Integration of the
bound electromagnetic
momentum. Here ˙.s
1
/
is the space-like hyperplane
transverse to the world line
z
.s/ intersecting it at the
proper time s
1
(similarly
˙.s
2
/). The hypersurfaces S
"
and S
R
are small and large
tubes around the world line
formed by sequences of the
2-spheres @Y
"
.s/ and @Y
R
.s/
for s 2 Œs
1
;s
2
. The domain
Y.s
2
/ ˙.s
2
/ (similarly
Y.s
1
/) is the 3-annulus
between @Y
R
.s
2
/ and @Y
"
.s
2
/
s
1
s
2
S
ε
Σ
(s
1
)
∂
Y
R
(s
1
)
Y ( s
2
)
S
R
z
µ
(s)
∂
Y
ε
(s
1
)
p
bound
D
Z
S
R
T
bound
dS
Z
S
"
T
bound
dS
; (34)
in view of the conservation equation for T
bound
outside the world line, see the remark
after Eq. 14. Here the integration elements dS
are directed outward to the world
line. The contribution from the distant surface S
R
vanishes if one assumes that
the acceleration is zero in the limit s !1[28]. This is nontrivial: though the
stress tensor (12) decays as R
3
at spatial infinity, the corresponding flux does
not vanish a priori, because the surface element contains a term (proportional to
the acceleration) which asymptotically grows as R
3
. As a consequence, the sur-
viving term will be proportional to the acceleration taken at the instant s
ret
of the
proper time, where s
ret
!1in the limit R !1. Finally, we are left with
the integral over the inner boundary S
"
only. To find an integration measure on
S
"
we foliate the space-time domain shown in Fig. 1 by the hypersurfaces ˙.s/
parameterized by the spherical coordinates r;
1
D ;
2
D '. Introducing the
unit space-like vector n
.s;
i
/; n
n
D1 transverse to v
,weusethecoor-
dinate transformation x
D z
.s/ C rn
.s;
i
/. The induced metric on S
"
reads
dS
D "
2
Œ1 ".an/n
dsd˝, and hence
dp
bound
ds
D
Z
S
"
"
2
Œ1 ".an/
F
T
bound
n
d˝; (35)

376 D. Gal’tsov
where the limit " ! 0 has to be taken. One has to expand
F
T
bound
in terms of ".
In fact, the energy–momentum tensor depends on the space-time point x
through
the quantity , depending directly on x
, and also through the retarded proper time
s
ret
. We have to express the resulting quantity as a function of the proper time s
corresponding to the intersection of the world line with the space-like hypersurface.
We write T
bound
in terms of the null vector R
D c
:
4
e
2
T
bound
D
a
.
R
/
4
C
.2.aR/ 1/ R
R
6
C
.1 .aR// v
.
R
/
5
2
4
; (36)
and expand R
as
R
D x
z
.s
ret
/ D "n
C v
1
2
a
2
C
1
6
Pa
3
C O.
4
/; (37)
where D s s
ret
>0and all the vectors are taken at s. This expansion in powers
of has to be rewritten in terms of ". The relation between the two can be found
from the condition R
2
D 0:
D " C
an
2
"
2
C
9.an/
2
C a
2
4 Pan
"
3
24
C O."
4
/: (38)
Substituting this into Eq. 37 and further to (36) we find:
p
bound
D
e
2
4
s
2
Z
s
1
ds
n
2"
2
C
a
2"
C
.an/
2
Ca
2
=3
v
C
.an/
2
C a
2
=2
n
2 Pa
=3 C 3.an/a
=4
d˝: (39)
The leading divergent term 1="
2
disappears after angular integration. Thus we
obtain [11]:
f
bound
D
dp
bound
ds
D
e
2
a
2"
C
2e
2
3
Pa
: (40)
Here the first divergent term has to be absorbed by the renormalization of mass,
while the second is the finite Schott term. Comparing this with (28) we confirm the
identity (22). Note that a priori the regularization parameter " here (the radius of the
small tube) is not related to the splitting parameter of the delta-function in the previ-
ous local force calculation. But actually they give the same form for divergent terms,
for which reason we use the same symbol " for both of them. With this convention,
the divergent terms in the momentum conservation identity (22) mutually cancel.
The significance of the Schott term in the balance of momentum between the ra-
diating charge and the emitted radiation is not always recognized in the textbooks on

Radiation Reaction and Energy–Momentum Conservation 377
classical electrodynamics. Instead, its presence is often interpreted as a drawback of
classical theory, since formally it may lead to self-accelerating solutions. Meanwhile
such solutions must be discriminated as unphysical since they do not satisfy proper
initial/final conditions that should be imposed on the third-order equation of mo-
tion [17]. From the above analysis it is clear that the Lorentz–Dirac equation,
although formulated in terms of particle variables, actually describes the composite
system consisting of a charge and its bound electromagnetic momentum. The redefi-
nition of the particle momentum joining to it the bound electromagnetic momentum
obscures the problem of interpretation. It is better to think of the Schott term as the
field degree of freedom and interpret the Lorentz–Dirac equation as the momentum
balance equation for the total system including the electromagnetic field.
An instantaneous momentum balance is not just the balance between the particle
and radiation, the energy–momentum can be also transferred between the particle
and the field coat bound to it. Or, the radiated momentum is not always taken from
the mechanical momentum of the charge, but by virtue of the Schott term, it can be
extracted from the field coat too. This is what happens in the case of the uniformly
accelerated charge, when the total reaction force instantaneously is zero, while
radiation carries the momentum away at a constant rate. The balance in ensured by
the Schott term. However, the constant acceleration cannot last infinitely long. One
has to consider the switching on/off processes in order to understand that finally
the energy–momentum of radiation is taken from the particle. This consideration
clarifies the necessity of the time averaging or integration over time needed to
establish the momentum balance between radiation and the source particle. The
equation of motion including the reaction force instantaneously does not imply
the equality of the radiative momentum loss and the particle momentum. This fea-
ture is general enough, it is also applicable to radiation of nongravitational nature
from particles moving along the geodesics in curved space-time, as well as to the
gravitational radiation.
2.3 The Rest Frame (Nonrelativistic Limit)
In the rest frame of a charge the recoil force has no spatial component. This is due
to the fact that radiation in two opposite directions is the same so that the spatial
momentum is not lost by radiation, though the energy is lost. Hence the total spatial
component of the reaction force is presented by the Schott term, namely
f
Schott
D
2
3
e
2
P
a: (41)
The work done by this force,
Z
f
Schott
vdt D
Z
2
3
e
2
P
a vdt D
Z
2
3
e
2
a
2
dt C boundary terms; (42)
correctly reproduces the radiative loss in the rest frame. (Boundary terms should
vanish by appropriate asymptotic switching on/off or periodicity conditions.)

378 D. Gal’tsov
3 Flat Dimensions Other than Four
Recent interest to models with large extra dimensions motivates the study of
radiation and radiation reaction in dimensions other than four. It turns out that the
radiation picture is substantially different in even and odd dimensions because of
the different structure of the retarded Green’s functions for massless fields in the
coordinate representation [10] (they still look similarly in all dimensions in the
momentum representation). In even dimensions the retarded potential is localized
on the past light cone (Huygens principle) so the situation is qualitatively similar to
that in the 4D case. In odd dimensions it is nonzero also inside the past null cone
though radiation still propagates along the null rays. In 3D, for instance, the scalar
Green’s function reads
G
3D
ret
.X/ D #.X
0
/#.X
2
/.X
2
/
1=2
;X
D x
x
0
: (43)
It does not contain the “direct” part singular on the light cone. Green’s functions
in higher odd dimensions D D 2n C 1 can be obtained by the recurrent relation
[10,12]
G
2nC1
ret
.X/
dG
2n1
ret
dX
2
; (44)
In particular, in 5D
G
5D
ret
.X/ #.X
0
/
ı.X
2
/
.X
2
/
1=2
1
2
#.X
2
/
.X
2
/
3=2
; (45)
both the direct and the tail parts are present. It turns out that the direct part regular-
izes the tail contribution to the field stress proportional to the derivative of G that
otherwise would be singular outside the world line.
In even dimensional space-times the split of the retarded potentials into the time
symmetric and the radiative parts leads to purely divergent self-force and a finite
radiative part:
f
self
D f
div
;f
rad
D finite: (46)
Divergent terms are Lagrangian type and can be absorbed by introducing suitable
counter-terms. Since the Coulomb dependence is more singular at the location of the
source in higher dimensions, the self-action gives rise to larger number of divergent
terms 1="
n
,wheren is changing from unity to the integer part of D=2 1.The
highest divergence is absorbed by the renormalization of mass, while to absorb other
divergences additional counter-terms are needed depending on higher derivatives
of the velocity. These are not present in the initial action, so higher-dimensional
classical theories are not renormalizable. In 6D one has two divergent terms (which
in terms of the field split correspond to f
self
[18]):
f
div
D
1
6"
3
a
C
1
2"
3
4
v
. Paa/ C
3
8
a
2
a
C
1
4
Ra
; (47)

Radiation Reaction and Energy–Momentum Conservation 379
the leading term being eliminated by the mass renormalization and the subleading
requiring the counter-term [18]
S
1
D
.1/
0
Z
.Rz/
2
ds; (48)
which leads to the Frenet–Serret dynamics [1] unless the renormalized value
.1/
0
D
0. For each two space-time dimensions one new higher-derivative counter-term is
needed to absorb divergences.
The split of the field stress tensor built with the retarded field into the sum of the
emitted and bound terms is also possible in all even dimensions, and one always has
the relation (22). In 6D, for example, the radiation recoil force in 6D is
f
emit
D
4
45
e
2
Pa
2
v
C
2
21
.a Pa/a
2
9
a
4
v
2
105
a
2
Pa
; (49)
and the Schott terms is
f
Schott
D
4e
2
45
«a
C
16
7
a
2
Pa
C
60
7
.a Pa/a
C 4 Pa
2
v
C 4.aRa/v
; (50)
the sum of two being orthogonal to the 6-velocity. The Schott terms is again given
by the finite part of the integrated bound momentum.
In odd dimensions one always has tail terms. A split of the retarded field into the
self and the radiative parts is always possible, and the substitution into the equations
of motion leads to divergent and finite terms. Divergent ones can again be absorbed
introducing the counter-terms. The split of the stress–tensor into the emitted and the
bound parts is more subtle. The situation is obscured by the fact that though the free
field is massless and thus propagates along the null cone, the full retarded potential
fills the interior of the past light cone. Still one is able to obtain the general formula
for radiation momentum that is no more associated with the retarded proper time on
the world line [13].
4 Local Method for Curved Space-Time
An approach initiated by DeWitt and Brehme and further applied to linearized
gravity in [20] appeals to computation of the integral of the stress tensor in the
world-tube surrounding the world line. This is similar to our calculation of the bound
momentum. However, in curved space-time the split of the stress tensor into the
emitted and the bound parts becomes problematic, so the complete analysis of the
balance between radiation, the kinetic momentum, and the bound momentum is not
available. Meanwhile, to compute the total reaction force one can use a much sim-
pler calculation substituting the retarded field directly into the equations of motion
[14]. This approach was also formulated in higher even-dimensional space-time in
the paper [12] which we follow here.

380 D. Gal’tsov
4.1 Hadamard Expansion in Any Dimensions
As in D D4 [5], the curved space Green’s functions for massless fields in other
dimensions can be constructed starting with the Hadamard solution. For sim-
plicity we consider here the scalar case. The scalar Hadamard Green’s function
G
H
.x; x
0
/ is a solution of the homogeneous wave equation
x
G
H
.x; x
0
/ D0;
where Dg
r
r
. The procedure consists in expanding G
H
.x; x
0
/ in terms
of the Synge world function .x;x
0
/.ForD D4, the Hadamard expansion contains
two terms singular in , namely,
1
and ln . In higher dimensions one has to add
other singular terms, and by dimensionality it is easy to guess that each dimension
introduces an additional factor
1=2
. Thus, the Hadamard expansion in D D2d
dimensions (d > 3=2 is integer or half-integer) generically must read
G
H
.x; x
0
/ D
1
.2/
d
"
D
X
nD1
g
n
1n=2
C v ln
#
; (51)
where g
n
Dg
n
.x; x
0
/; v Dv.x; x
0
/ are two-point functions. It can be shown, that
in odd dimensions we actually have only odd powers of
1=2
,andineven
dimensions – only even powers, that is, an expansion in terms of inverse integer
powers of . The logarithmic term is present only in even dimensions.
Substituting (51) into the wave equation, in the leading singular order we will
have g
D
D
1=2
: In the next to leading order we obtain the equation:
2@
g
D1
C g
D1
.D 1/g
D1
D 0: (52)
which does not have analytic solutions, so g
D1
D0.ForD D3 this means the
absence of the logarithmic term. Similarly, considering the equation for g
.D12k/
,
k 2 N,wefindg
D12k
D 0: This means that for an even-dimensional space-time
the Hadamard Green’s function contains only integer negative powers of plus
logarithm and a regular part, while in the odd-dimensional case – only half-integer
powers of plus a regular part.
For the sequence of Green’s functions in the flat space-time, the one in
D C2 dimension is proportional to the derivative of the Green’s function in
the twice preceding dimension D. In fact, in even dimensions the symmet-
ric Green’s function is the derivative of the order d 2 of the delta-function:
G
D
ı
d 2
./; D.x x
0
/
2
=2 and thus, G
DC2
dG
D
=d. Applying regular-
ization, ı..x x
0
/
2
/ D lim
"!C0
ı.j.x x
0
/
2
j"
2
/; we obtain
G
DC2
dG
D
=d"
2
: (53)
This relation has a consequence that the Laurent expansion of the Lorentz–Dirac
force in terms of " in the even-dimensional Minkowski space has only odd negative
powers, and no even terms. So the number of divergent terms in the self-action in-
creases by one for each next even dimension. In curved space passing to the standard
notation for g
n
we have
