Blanchet L., Spallicci A., Whiting B. (Eds.) Mass and Motion in General Relativity

Подождите немного. Документ загружается.

Radiation Reaction and Energy–Momentum Conservation 391

and X

D x

z

.t/: Using this source one can calculate the gravitational force and

ﬁnd the gravitational Schott term

Gshott

D

G

;D

C m

; (102)

where D

is the quadrupole moment.

Note that this derivation of the Schott term is not based on the local calcula-

tion, the two-body treatment was necessary. These features seem to be general:

gravitational radiation reaction from a non-geodesically moving particle cannot be

described by some DeWitt–Brehme-type equation.

6 Conclusions

The purpose of this lecture was to discuss some subtle points associated with in-

terpretation of the radiation reaction force. We have shown that the Lorentz–Dirac

equation in classical electrodynamics describes the balance of three and not just two

momenta: the mechanical momentum of the particle, the momentum of emitted ra-

diation, and the momentum carried by the electromagnetic ﬁeld bound to the charge.

The total momentum is conserved, but this does not imply an instantaneous balance

of the emitted momentum and that of the particle. The bound ﬁeld momentum de-

scribed by the Schott terms destroys the local balance. The total balance, however,

is restored if one consider the situation when the charge has zero acceleration at

the initial and ﬁnal moments, or for a periodic motion subject to averaging. These

considerations are equally applicable to radiation reaction of a charge in curved

space-time and for gravitational radiation reaction. This explains, in particular, the

necessity of averaging in calculating the evolution of the Carter constant in the Kerr

ﬁeld [27].

A novel feature related to curved space is the existence of the ﬁnite DDSW force

arising due to the tidal deformation of the bound electromagnetic ﬁeld of the charge.

This force is often interpreted as part of radiation reaction force, but one has clearly

understood, however, that it has nothing to do either with radiation or with the Schott

force. As we have shown, it is given by the T-even part of the retarded ﬁeld, and thus

represents a ﬁnite remnant from the mass renormalization.

Derivation of the reaction force of nongravitational nature acting on a charge

moving (both geodesically and non-geodesically) in curved space-time can be com-

puted by directly substituting the retarded ﬁeld into the equations of motion, as in

the Minkowski space. The regularization is easily achieved by the point-spliting, and

divergences are eliminated by renormalization of mass. In higher dimensions one

needs counter-terms depending on higher derivatives of the velocity. Divergences

may contain the Riemann tensor of the background.

Gravitational radiation reaction force can be obtained in a way similar to a

nongravitational one only in vacuum space-time. In non-vacuum background the

392 D. Gal’tsov

source of radiation apart from the local contribution from the particle must contain

the contribution from the perturbed background. This can be seen from the analysis

of the Bianchi identity. This second contribution is nonlocal, so the possibility to

obtain the equation of the DeWitt–Brehme type seems implausible.

For a non-geodesically moving mass the formal derivation of the reaction force

leads to putative antidamping effect. To cure this problem one has to take into

account the contribution of stresses forcing the mass to accelerate. Then in the

nonrelativistic case one derives the gravitational quadrupole Schott term, but the

derivation is nonlocal. This is another example when the (quasi)local equation of

motion with the reaction force does not exist. Here by quasilocality we mean the

possibility of the tail term.

Acknowledgements The author is grateful to the Organizing Committee for invitation and support

in Orl´eans. Useful discussions with the participants of the School on Mass and Capra conference

are acknowledged. Most of the results presented in this lecture were obtained in collaboration

with Pavel Spirin, to whom the author in indebted. The work was supported by the RFBR project

08-02-01398-a.

References

1. G. Arreaga, R. Capovilla, J. Guven, Class. Quant. Grav. 18, 5065 (2001)

2. S.M. Christensen, Phys. Rev. D 14, 2490 (1976)

3. S. Detweiler, Class. Q. Grav. 22, S681 (2005)

4. S. Detweiler, B. F. Whiting, Phys. Rev. D 67, 024025 (2003)

5. B.S. DeWitt, R.W. Brehme, Ann. Phys. (N.Y.) 9, 220 (1960)

6. C.M. DeWitt, B.S. DeWitt, Physics 1, 3 (1964)

7. P. Dirac, Proc. R. Soc. Lond. A 167, 148 (1938)

8. T. Fulton, F. Rohrlich, Ann. Phys. (N.Y.) 9, 499 (1960)

9.D.V.Gal’tsov,J.Phys.A15, 3737 (1982)

10. D.V. Galtsov, Phys. Rev. D 66, 025016 (2002)

11. D.V. Gal’tsov, P. Spirin, Grav. Cosmol. 12, 1 (2006)

12. D.V. Galtsov, P.A. Spirin, Grav. Cosmol. 13, 241 (2007)

13. D.V. Galtsov, P.A. Spirin, Radiation in odd dimensions, in preparation

14. D. Gal’tsov, P. Spirin, S. Staub, in Gravitation and Astrophysics, ed. by J.M. Nester, C.-M.

Chen, J.-P. Hsu (World Scientiﬁc, Singapore, 2006), p. 345, arXiv:gr-qc/0701004v1 (2006)

15. S.E. Gralla, R.M. Wald, Class. Q. Grav. 25, 205009 (2008)

16. J.M. Hobbs, Ann. Phys. (N.Y.) 47, 141 (1968)

17. D. Ivanenko, A. Sokolov, Sov. Phys. Doklady 36, 37 (1940); in Russian, Classical Field Theory

(Gostehizdat, Moskva, 1948); in German, Klassische feldtheorie (Akademie Verlag, Berlin,

1953)

18. B.P. Kosyakov, Theor. Math. Phys. 199, 493 (1999)

19. B.P. Kosyakov, Introduction to the Classical Theory of Particles and Fields (Springer, Berlin,

2007)

20. Y. Mino, M. Sasaki, T. Tanaka, Phys. Rev. D 55, 3457 (1997)

21. C. Morette-DeWitt, J. L. Ging, C. R. Acad. Sci. Paris 251, 1868 (1960)

22. E. Poisson, Living Rev. Rel. 7,URL:http://www.livingreviews.org/lrr-2004-6

23. F. Rohrlich, Nuovo Cimento 21, 811 (1961)

24. F. Rohrlich, Classical Charged Particles, 2nd edn. (Addison-Wesley, Reading, MA, 1965;

Redwood City, CA, 1990)

Radiation Reaction and Energy–Momentum Conservation 393

25. J.M. Sanchez, E. Poisson, arXiv:gr-qc/0512111v2 (2007)

26. A.G. Smith, C.M. Will, Phys. Rev. D 22, 1276 (1980)

27. T. Tanaka, Prog. Theor. Phys. Suppl. 163, 120 (2006)

28. C. Teitelboim, Phys. Rev. D 1, 1572 (1970)

29. C. Teitelboim, D. Villarroel, Ch. G. van Weert, Riv. Nuovo Cimento 3, 1 (1980)

The State of Current Self-Force Research

Lior M. Burko

Abstract We brieﬂy review some of the issues relevant to self-force research.

We consider frequency-domain and time-domain approaches, adiabatic and post-

adiabatic waveforms, the need for a revised regularization method for 2C1D

numerical-simulations, the so-called m-mode regularization, and the need for

second-order self-forces and their effect on the gravitational waveforms.

1 Introduction

The two-body problem in General Relativity has been practically solved only re-

cently, 90 years after the formulation of the theory [3, 16,42]. The solution for two

bound gravitating bodies, including their combined gravitational ﬁeld, is numeri-

cal, and exhibits the rich strong nonlinear dynamics that characterizes the problem.

Indeed, numerical relativity has made impressive progress over the last couple of

years, and is now routinely used to study phenomena such as spin ﬂips and kick ve-

locities in binary black hole mergers (see, e.g., [2,17] and references cited therein).

The typical numerical relativity problem involves two objects of comparable

masses. Therefore, the dynamical timescale for the problem in the strong-ﬁeld

regime is comparable to the orbital period. Speciﬁcally, the binary merges within a

few orbits, starting with initial separation comparable to the system’s mass. The sit-

uation is quite different when the masses of the two members of the binary are very

different. In the extreme mass ratio case the system exhibits two distinct timescales,

namely the orbital period timescale and the binary evolution timescale, the latter

being much greater than the former. Full numerical relativity simulations would

therefore be a wasteful approach to undertake: the binary evolves over very many

orbits. Indeed, for typical extreme mass-ratio inspirals (EMRIs) of astrophysical

L.M. Burko (



)

Department of Physics and the Center for Space Plasma and Aeronomic Research,

University of Alabama in Huntsville, Huntsville, AL 35899, USA

e-mail: burko@uah.edu

L. Blanchet, A. Spallicci, and B. Whiting (eds.), Mass and Motion in General Relativity,

Fundamental Theories of Physics 162, DOI 10.1007/978-90-481-3015-3

14,

 Springer Science+Business Media B.V. 2011

395

396 L.M. Burko

interest the expected number of orbits is in the range 10

– 510

. Speciﬁcally, for a

binary with masses M and  M , the orbital timescale M , and the inspiral time-

scale M

=, which is longer than the orbital timescale by a factor of M= 1.

The number of orbits therefore scales with M=. Following a full numerical relativ-

ity simulation over this many orbits is as yet impossible, and certainly is impractical.

Instead, the two very different timescales suggest a different approach, based on adi-

abatic evolution of the system. The extreme mass ratio of the two members of the

binary suggests the use of perturbation theory, with the smallness parameter being

the binary’s mass ratio =M .

Perturbation theory simpliﬁes the problem in some sense, although practically

the problem is as yet unsolved, as can be attested by the papers in these Proceedings.

The introduced simplicity of a point particle brings with it an entire Pandora’s box of

problems: Is the model of a point particle self-consistent within General Relativity?

In this chapter we focus our overview on the frequency-domain (FD) and time-

domain (TD) approaches to calculate EMRIs, with the objective of ﬁnding accu-

rate gravitational wave templates. Regularization methods are discussed elsewhere.

An important requirement for such templates is that the source parameters span a

very wide range in eccentricities. EMRIs in the good-sensitivity frequency band for

LISA are expected to span a wide range in eccentricities. Speciﬁcally, such sources

are believed to be created as a result of the compact object’s scattering by multi-body

interactions onto a highly eccentric orbit in the spacetime of the central black hole.

For central black holes with mass of M D 310

it was shown by Hopman and

Alexander [31] that the probability distribution function of compact objects entering

the LISA band with eccentricity " in the range 0  "  0:81 peaks for "  0:60:7.

Intermediate mass black holes would have even higher eccentricities. Speciﬁcally,

it was shown in [31] that for a central black hole of M D 10

the maximal

eccentricity is "

max

D 0:998 and all inspiraling compact objects (except for white

dwarfs that are likely to be tidally torn) are likely to have eccentricities close to the

maximal value. The wide range of eccentricities of possible LISA EMRI sources

raises the question of how the construction of theoretical templates depends on the

parameters of the EMRI. Speciﬁcally, we are interested in how different approaches

to compute theoretical gravitational-wave templates depend on the eccentricity.

Construction of theoretical templates is important both for detection of EMRIs

gravitational waves and for accurate parameter estimation. Numerical waveforms

can be constructed using the FD or the TD approaches. The former approach has

been developed to very high accuracy, and is considered robust and accurate [1,18–

20,26,28,32,33,38,39,46,49–51]. On the other hand, advances to the TD approach

have been hindered ﬁrst by the success of the FD approach [29,32], and by the cru-

dity of the initial attempts to evolve numerically the ﬁelds coupled to a point-like

source with the Teukolsky equation [34, 37]. Signiﬁcant improvement in the accu-

racy of TD solutions of the inhomogeneous Teukolsky equation, that is, the 2C1D

solution of the Teukolsky equation coupled to a point mass, was recently achieved

in [15, 47]. For the ﬁrst time, it was shown that TD calculations can be as accu-

rate as FD calculations. The TD method of [15] was improved with the introduction

of the “discrete delta” model of the source [47] and an appropriate low pass ﬁl-

The State of Current Self-Force Research 397

ter that makes the discrete delta useful also for eccentric or inclined orbits [48].

Speciﬁcally, correlation integrals of gravitational waveforms sourced by generic or-

bits (i.e., inclined and eccentric orbits) done for the same system in the FD and TD

approaches show that the two agree to a high level [48]. One may therefore argue

that the two methods are comparable in the results they are capable of producing.

We therefore contend that the viewpoint that the TD solution of the inhomogeneous

Teukolsky equations is far from being competitive from the FD solution can no

longer be supported. However, we believe that one should not seek competition of

the two approaches, but rather how they complement each other, as either method

has nonoverlapping strengths.

The organization of this paper is as follows. In Section 2 we discuss the

Teukolsky equation, and its use for ﬁnding adiabatic waveforms, followed by a

procedure based on the linearized Einstein equations in the Lorenz gauge. In Sec-

tion 3 we discuss the FD approach for calculating the self-force, and in Section 4

the TD counterpart. Finally, in Section 5 we discuss post-adiabatic waveforms and

the importance of second-order self-forces.

2 The Teukolsky Equation

2.1 The Inhomogeneous Teukolsky Equation

with a Distributional Source

The Teukolsky equation, that governs the perturbations of Kerr geometry in Boyer–

Lindquist coordinates with a matter-source term, is given by [52]



C a



 a

sin





4Mar



@t@







sin





@



s





sC1





sin 

@



sin 

@



 2s



a.r  M/



i cos 

sin





2s



M.a

 r



 r  ia cos 





cot

  s



D4.r

C a

cos

/T; (1)

where  D r

 2Mr C a

and T D 2

4

,where



 C 3  



C 4 C 







 2



C 2˛









 C 2  2



C 













 



C ˇ



C 3˛

C4/



 C 2 C 2













 



C 2ˇ



C 2˛





: (2)

Here,  WD  1=.r  ia cos /. All the symbols used above are deﬁned in [52].

By choosing their values in Boyer–Lindquist coordinates and expressing Eq. 1

398 L.M. Burko

explicitly, we obtain an explicit but quite complicated form for the source term.

The Teukolsky function is a gauge-invariant projection of the Weyl tensor on the

null legs of the Kinnersley tetrad. Speciﬁcally, it is

WD  C

˛ˇ  ı



There is also a comparable equation for

WD  C

˛ˇ  ı



. Note, that

although

and

are gauge invariant, they are tetrad dependent.Itisthere-

fore important that they are projected off the Weyl tensor in the Kinnersley tetrad.

The major problem with evaluating self-forces using the Teukolsky equation ap-

proach is the reconstruction of the metric perturbations needed for the determination

of the self-force, including the problem of ﬁnding the contributions of the non-

radiative modes ` D0; 1,where` is the colatitude number.

One technical difﬁculty associated with the source term on Eq. 1 is that it includes

not just delta functions, but also their gradients. Several approaches to the numerical

modeling of these distributions have been attempted [15, 47].

2.2 Adiabatic Waveforms

The source term for the Teukolsky equation (1) depends on an integral over the

world line of the orbiting particle, speciﬁcally the various projections of the

stress-energy tensor on the null tetrad vectors. The most immediate problem is

that the complete history of the source term includes the radiation-reaction af-

fected world line, which is the very quantity we are seeking.

Several approaches to address this difﬁculty have been proposed. The simplest

approach, undertaken in [32], is to approximate the world line as a Kerr geodesic

orbit. This approximation is valid in the adiabatic limit, and is useful to ﬁnd the

ﬁrst-order radiative correction. The approach suggested in [32] is to model the short

timescale by geodesic Kerr motion, with constant constants of motion. The latter

vary appreciably only on longer timescales, such that they are not constants of the

motion in the strict sense, but would be in the absence of radiation-reaction effects.

The short timescale pieces are then connected by making small adjustments to the

constants of the motion, in a manner that preserves global conservation laws by

means of the ﬂuxes of energy and angular momentum to inﬁnity and down the event

horizon of the Kerr black hole. This approach is complicated by the third constant

of the motion, namely the Carter constant. The latter, being essentially the square

of the angular momentum, is a nonadditive constant of motion in the absence of

radiation reaction. One may therefore not associate “this much” Carter constant to

this part of space, and “that much” to another because of essentially self-interference

effects. The evaluation of the rate of change of Carter’s constant normally requires

the local self-force, and therefore the so-called radiation reaction without radiation-

reaction approach has limited applicability, and cannot address generic cases. The

nonadditivity of Carter’s constant implies that one may not use balance arguments as

with the ﬂuxes of energy and angular momentum, and one must then seek alternative

methods for evaluating the rate of change of Carter’s constant.

The State of Current Self-Force Research 399

2.3 Numerical Solution of the Teukolsky Equation

Direct numerical solutions of the Teukolsky equation (1) is problematic because

of its long-range effective potential. At great distances, r



!1,wherer



is the

“tortoise coordinate,” the outgoing and incoming solutions behave like e

i!r



and

4

i!r



, respectively. The latter then are swamped by the former, and the solu-

tion becomes inaccurate. The solution for this problem is to solve in practice the

Sasaki–Nakamura equation, that enjoys a shorter effective potential, and therefore

does not share the technical problem of its Teukolsky counterpart. The solutions to

the Sasaki–Nakamura equation and the Teukolsky equation are related by a trans-

formation that can be calculated accurately anywhere, including the radiation zone.

Therefore, one may in practice solve the Sasaki–Nakamura equation, and then trans-

form the solutions to the solutions of the Teukolsky equation, without ever needing

to solve directly the latter.

For generic orbits, when working in the FD one needs to sum over harmonics of

the three fundamental frequencies, namely, ˝



, ˝



,and˝

. When the orbits are

relatively simple, the number of modes to be summed over is easily manageable, and

the FD approach leads to a fast and accurate solution, exhibiting the so-called voices

of the gravitational waveforms. It is important to emphasize that for such orbits

the FD calculation is much more computationally efﬁcient than its TD counterpart.

However, for generic orbits, the situation is quite different. Already for equatorial

orbits, the number of modes to be calculated for waveforms calculated at a given

accuracy level grows fast with the eccentricity of the orbit, as was shown recently by

Barton et al. [11]. Indeed, Drasco has shown how the different overtones are excited

and evolve during the motion, and in particular how their number and distribution

evolve [25].

In contrast, the TD calculation time does not show such a strong dependence

on the eccentricity of the orbit. When a ﬁxed spatial and temporal grid density is

used, the calculation time is even independent of the orbital parameters [11]. Weak

dependence of the computation time is found, however, when the grid parameters

are optimized for the orbital parameters, for example, when the grid parameters are

taken to be the coarsest that give rise to the desired accuracy level. The TD calcula-

tion may be faster than a FD calculation for the same orbit and the same accuracy

level, speciﬁcally when the orbital eccentricity is very high. At lower eccentricities,

the FD calculation would be faster. It therefore makes sense that in practice certain

parts of the parameter space would be calculated with one method, and other parts

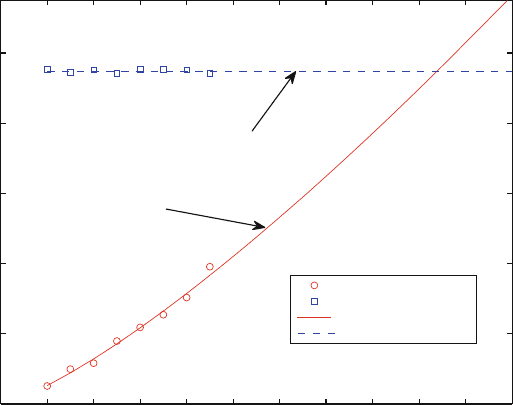
of the parameter space with another. Figure 1 shows the comparison of the compu-

tational time for individual azimuthal modes m for a particular orbit for FD and TD

calculations. Typically, the TD computation time is insensitive to the value of m,but

the FD computation time increases fast with m. One should bear in mind, however,

that with a ﬁxed grid resolution, one is in practice limited in the resolution of high

m (and therefore also `) modes, so that the  resolution is limited. Increasing the

grid density to enhance the  resolution would shift the entire TD curve upward.

One may of course adapt the grid angular resolution to the calculated mode, which

is expected to result in an increasing computational time as a function of the mode

number m. Quantitative studies of this question are yet to be done.

400 L.M. Burko

0 2 4 6 8 10 12 14 16 18 20 22

200

400

600

800

1000

Computation time [sec]

FD computation time

TD computation time

FD model

TD model

Fig. 1 The computation time of individual azimuthal m modes in a frequency-domain (FD) and

a time-domain (TD) computation. The orbit has semilatus rectum p D 4:64M , and eccentricity

" D 0:5, and the black hole spin is a D 0:5M . The FD results (in 2C1D simulations) are shown

in circles, and the TD results in squares. For more detail, see [11]

One difﬁculty of the inhomogeneous Teukolsky equation is that the source term

includes derivatives of delta functions. These derivatives are a source for high-

frequency numerical noise in the TD, which needs to be removed either by the

introduction of a low pass ﬁlter (as was done in [47]), or by introducing artiﬁcial

viscosity.

2.4 The Linearized Einstein Equations

Another approach is to write directly the linearized Einstein equations in the Lorenz

gauge. The source term for the linearized Einstein equations includes only delta

functions, but not their derivatives. Therefore, there is reason to expect numerical

noise production to be lower than in the case of the Teukolsky equation. Of course,

the solution of the linearized Einstein equations involves the solution of 10 coupled

wave equations, in addition to 4 gauge conditions that need to be monitored or even

enforced. The ﬁeld equations take the form

˛ˇ

C 4g

ı





.˛

ˇ/;ı

C 2

.˛



ˇ/



.˛ˇ/

C 2R



˛ˇ



D16 T

˛ˇ

;

(3)