Blake A.J.(ed.) Crystal Structure Analysis

Подождите немного. Документ загружается.

62 Background theory for data collection

full data set), equivalent reﬂections can be merged to afford a more

reliable unique data set that one would otherwise have had. However,

the converse is an unhelpful outcome: collecting data assuming too high

a crystal system initially is likely to render a dataset useless because it

lacks key unique data from whole segments of reciprocal space (see

Section 5.6.1).

5.5 Relating diffractometer angles to unit

cell parameters: determination

of the orientation matrix

Amodern-day area-detector-based diffractometer will typically possess

three or four independent motors that, together, are able to drive the

crystal sample into nearly any orientation with respect to the incident

X-ray beam. The associated angular degrees of freedom for each motor

are usually called φ,2θ , ω, and κ, where φ represents the rotation of the

sample about the vertical axis of the goniometer head, 2θ represents

the movement of the detector relative to the incident X-ray beam, ω

concerns the rotation of the base of the diffractometer about its physical

vertical axis and is usually constrained to ‘bisecting geometry’, whereby

2θ = ω, and κ is the motor that provides vertical tilt of the goniometer

head. Figure 5.6 illustrates these deﬁnitions in geometrical terms.

The angular positions of each motor must be deﬁned relative to a

ﬁxed origin; the x, y, z diffractometer axes provide the co-ordinate basis

set for this purpose. By convention, the z-axis is usually deﬁned to be

coincident with the diffractometer φ-axis. x and y are deﬁned arbitrarily

to complete a right-handed set; the deﬁnitions are not the same for all

D = Detector

(a) (b)

C = Crystal

M = Microscope

X = X-ray source

Fig. 5.6 (a) An annotated photograph of a CCD diffractometer. The crystal sample is

afﬁxed to the top of a goniometer head (b) that, in turn, is mounted onto the diffractometer

at position C.

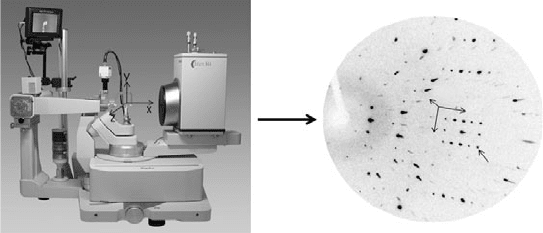
5.5 Relating diffractometer angles to unit cell parameters 63

types of diffractometer, but whatever their deﬁnition, they necessarily

allow a formula to deﬁne ω,2θ and κ in terms of x, y and z.

In order that these motors can be used to ‘dial up’ any (hkl) reﬂection

during an experiment, one needs to be able to relate the diffractometer

axes, x, y, z, that the motors are deﬁned upon, with the axes that deﬁne

a diffraction pattern for a given sample: the unit cell reciprocal axes;

thence, one can calculate h, k, l.A3× 3 matrix, called the ‘orientation

matrix’, enables this relation:

x = Ah,

where x and h represent the vectors, (x, y, z) and (h, k, l), respectively,

and A is the orientation matrix deﬁned by:

A =

⎛

⎝

∗

⎞

⎠

the nine elements of this matrix representing the components of the

reciprocal cell axes on each axis, x, y and z. See Fig. 5.7 for an illustration

of these axes and relationships.

These matrix elements also contain information about the unit cell

(requiring six parameters) and orientation of the crystal (three parame-

ters). Thus, where required, the unit cell parameters can be extracted:



−1

⎛

⎝

a.aa.ba.c

b.ab.bb.c

c.ac.bc.c

⎞

⎠

where A



is the transpose of the orientation matrix, A.

These interconversions also prove very useful when carried out in

reverse using the inverse of the orientation matrix; for example, during

the previously mentioned indexing procedure, where one wished to

x = Ah

(hkl)

Fig. 5.7 A pictorial representation of the relationship between x, y, z and a

∗

, b

∗

, c

∗

and hkl.

64 Background theory for data collection

identify (hkl) from a trial unit cell using a small reﬂection list deﬁned

only by diffractometer angles:

h = A

−1

5.6 Data-collection procedures

and strategies

5.6.1 Criteria for selecting which data to collect

The Fourier transform calculation, that permits the reciprocal-space to

real-space conversion of structure factors into electron-density maps

of crystal structures, requires, in principle, an inﬁnite number of data.

Naturally, such a requirement is not possible to achieve experimentally.

However, one can collect sufﬁcient data to render such a calculation

viable; one usually collects data up to acertain valuein 2θ (typically2θ =

◦

with Mo radiation) beyond which the intensities, and therefore the

structure-factor magnitudes, are so low that one can approximate them

to zero for all unmeasured data. Thus, the Fourier-transform calculation

can still be provided with values effectively up to inﬁnity. That said,

since a series of zero-valued terms will have null effect on an integral, in

practice one actually approximates the true integral, with inﬁnite limits,

to a summation with ﬁnite limits inh, k, l corresponding to the maximum

values of h, k, l, collected in a dataset.

The more data collected, the better this approximation. The standard

2θ = 50

◦

cut-off threshold for data collection usually proves entirely

satisfactory for most crystal-structure determinations. Occasionally, one

may wish to collect further in 2θ , if one perhaps wanted a particularly

precise crystal-structure determination. Conversely, one might collect

data with a lower 2θ cut-off threshold, where the intensity of diffraction

spots becomes negligible before this default limit, 2θ = 50

◦

, is reached,

as, for example, occurs commonly where structural disorder is present.

Data-collection time restraints may also affect this default threshold

choice, for example, if the unit cell is very large and so it would take

too much time to collect sufﬁcient data up to 2θ = 50

◦

; alternatively, if

the crystal is decaying over time, it would be prudent to collect all data

as fast as possible.

Crystals diffract in all directions and so it is important to collect

diffraction data over a wide proportion of the scattering sphere. How-

ever, if one knows the crystal symmetry of a structure, one may not need

to collect data through the complete 360

◦

since a diffraction pattern may

be replicated in octants, quadrants or hemispheres of this total sphere.

Indeed, a full sphere of data would be required only if the sample pos-

sessed a non-centrosymmetrictriclinic crystal structure. Where Friedel’s

law applies, half of a diffraction pattern should be equivalent to its other

half if the crystal structure is centrosymmetric. Thus, only a hemisphere

of data need be collected to obtain all unique data if one knew that

5.6 Data-collection procedures and strategies 65

a structure was centrosymmetric and triclinic. The Laue symmetry in

other crystal systems, in combination with Friedel’s law, dictates what

fraction of the total sphere will contain all of the unique reﬂections. For

example,in the monoclinic crystal system, one quadrant of data will con-

tainall unique reﬂectionsfor acentrosymmetric structure,whilst only an

octant of data needs to be collected for a centrosymmetric orthorhombic

sample to capture all unique data.

One can therefore set up a data-collection schedule that aims to

acquire only the required unique data, according to the crystal sym-

metry of the sample. This said, it is good practice, if time permits,

to collect some duplicate reﬂections, so-called ‘symmetry-equivalents’,

to improve one’s data quality: symmetry-equivalents should have

the same intensity and so can be averaged to provide a more sta-

tistically sound, merged dataset. It is also absolutely crucial, if one

is not sure about the crystal symmetry of the sample before data

collection, to collect data according to the lowest crystal symmetry pos-

sible, since one can always discard or ‘merge’ duplicate data after an

experiment if a sample turns out to possess crystal symmetry higher

than that expected, whereas one cannot restore reﬂections from parts

of the diffraction sphere if they were never collected. The measure-

ment of symmetry-equivalent data is very useful for other reasons in

any case; e.g. conﬁrming crystal symmetry, undertaking absorption

corrections, etc.

With all of these factors in mind, one should then ensure that the order

of reﬂectionscollected isthe most time efﬁcient. Fortunately, commercial

area-detector diffractometers nowadays possess software to calculate

automatically time-optimized schedules for data collection.

5.6.2 How best to measure data: the need

for reﬂection scans

Due to a combination of reasons (e.g. the actual quality of a crystal

sample,the intrinsic resolutionof adetector), all hkl reﬂections measured

are not delta functions (inﬁnitely sharp); rather, they have a ﬁnite width.

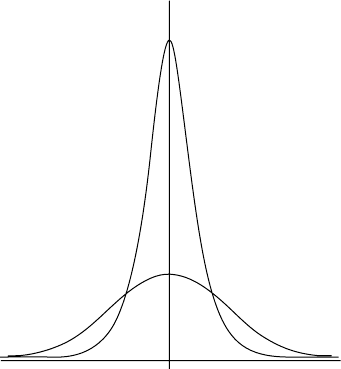
Therefore, in one dimension, a reﬂection proﬁle would look like one of

the curves in Fig. 5.8. The required intensity of a reﬂection is the area

under this curve. Consequently, one cannot just orient the crystal on

the diffractometer to the calculated 2θ value for a given hkl reﬂection

and measure the diffraction intensity with the crystal kept stationary.

One must rotate the crystal through the calculated position for each

reﬂection as it is measured in order to capture its full intensity. There

aretwo principalways that one can scanthrougha reﬂection when using

an area-detector diffractometer, and in either case, the axis of rotation is

usually ω or φ.

One approach is ‘narrow-frame’ scans: rastering through a reﬂec-

tion in incremental angular steps and building up a peak proﬁle from

the sequential ‘slices’ obtained for each peak. Each frame of data that

one collects using an area-detector diffractometer necessarily provides

66 Background theory for data collection

–1 –0.5 0 0.5 1

Fig. 5.8 Typical sharp and broad reﬂection proﬁles (the units are degrees).

a two-dimensional diffraction pattern. Therefore, each spot shown on a

frame of data represents a two-dimensional ‘slice’ of a reﬂection. If one

collects a series of such frames where only one diffractometer motor

is moved, in small angular increments, between the frames of data col-

lected, one can build up a peak proﬁle of each reﬂection on these frames,

assuming that there are sufﬁcient ‘slices’ for each reﬂection observed.

Figure 5.9 illustrates this process.

Alternatively, one can collect the whole intensity of a reﬂection in one

‘wide-angle slice’: sweeping through an angle greater than the angular

spread of a reﬂection whilst acquiring one frame of data.

The decision as to whether to collect data using wide or narrow scans

depends on several factors. One major advantage of wide-angle scans is

the speed of data collection: far fewer frames need to be collected com-

paredwith narrow-slice data collection;moreover, both data-acquisition

time and detector read-out time can represent the major contributions to

the overall data-collection time. However, there is limited scope for pro-

ﬁle analysis using wide scans; the accuracy of weak data may therefore

be compromised for data-collection speed. Certainly, if reﬂection pro-

ﬁles need to be analyzed, one must collect data using the narrow-frame

procedure.

When reﬂections appear close together in a diffraction pattern, where

the sample has one or more large unit cell parameters, wide scans may

become problematic, since two reﬂections appearing side-by-side on a

diffraction pattern may be collected in one wide scan and thence inter-

pretedas one reﬂection. One may overcome this barrier by extending the

crystal-to-detector distance from its default position; in such cases, how-

ever, two data collections are usually required to obtain the necessary

5.7 Extracting data intensities: data integration and reduction 67

(a) (b) (c) (d)

(e) (f) (g) (h)

(i) (j) (k) (l)

Fig. 5.9 Images of the same section of a detector from a series of data frames, collected

sequentially in incremental steps. The arrow in each frame points to a particular reﬂec-

tion, (hkl), which progressively ‘grows’ and then ‘fades’ as one motor moves by an angular

increment between each frame, which is about 1/6th of the full spread of the peak con-

cerned; the reﬂection thus appears clearly on 6 frames and its proﬁle can be built up by

plotting the 6 discs parallel to each other and interpolating between them to create a sphere

that represents the reﬂection intensity (the volume of the sphere).

data for structure solution, one at this extended crystal-to-detector

distance and the other at the default distance (see Chapter 6).

5.7 Extracting data intensities: data

integration and reduction

5.7.1 Background subtraction

Detector noise is present in all experimental data and the level of noise

varies from pixel to pixel in an area detector. One must thereforesubtract

this from the experimental signal in order to evaluate reliable diffraction

intensities. This is achieved by collecting one frame of ‘data’ with the

X-ray shutter closed so that no signal due to X-ray diffraction can be

present in this frame, only background noise. The data-acquisition time

of this ‘dark frame’ must match that which is proposed for the data-

collection frames. Then, one can simply subtract this dark frame – the

detector counts due to background noise – from each frame measured.

68 Background theory for data collection

123456789

! Averaged profile: section 1–>3

! Averaged profile: section 4–>6

! Averaged profile: section 7–>9

100

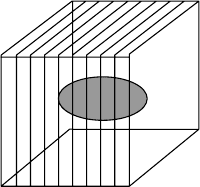
Fig. 5.10 A three-dimensional diffraction spot (left) is measured as 9 slices of two-dimensional data and integrated by summing the

pixel counts in each of these 9 frames (right) and interpolating between them.

5.7.2 Data integration

One extracts intensities from area-detector data via ‘integration’

(Kabsch, 1988). In its simplistic form, this involves the computer sequen-

tially scanning through each frame to build up a 3D image of each

reﬂection, putting a box around this constructed 3D spot, and trying

to ensure that a minimal amount of background is contained within the

box while not windowing out reﬂection intensity. For each reﬂection,

the summation of the detector counts registered in each pixel of the box

(i.e. its integrated volume) yields the intensity of that reﬂection.

Figure 5.10 illustrates this process. For weak reﬂections, it is difﬁcult

to extract the diffraction intensity from the background noise. Because

of this, the computer undertakes the integration process twice – the ﬁrst

time through it integrates all strong reﬂections (‘strong’ is distinguished

from ‘weak’ by a threshold value) and a library of their proﬁles is stored.

All weak reﬂections are simply ﬂagged as weak in this ﬁrst pass of inte-

gration. The integration process is then repeated for the weak reﬂections

with the proﬁles of strong reﬂections close in θ (and therefore resolu-

tion) being used to deﬁne the proﬁles of these weak reﬂections, so as

best to separate their signal from the background (Fig. 5.11). The model

proﬁle shapes are also used to calculate correlation coefﬁcients that can

be used to reject reﬂections.

5.7.3 Crystal and geometric corrections to data

Diffraction intensity for a given hkl reﬂection is directly proportional to

the square of the modulus of the structure factor, F, which is ultimately

5.7 Extracting data intensities: data integration and reduction 69

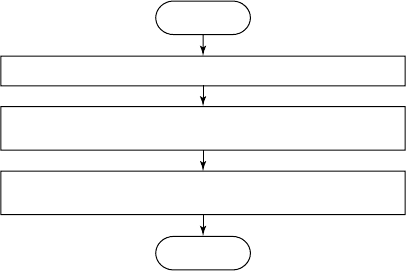
STOP

START

First pass of integration (processes strong reflections)

Library of strong reflection profiles created

(in bins of similar resolutions)

Second pass of integration

(use of libraries to model weak reflections)

Fig. 5.11 Flow diagram of the modelling of weak reﬂections by proﬁle analysis.

what we want to calculate in order to solve a structure. There are various

factors that, when evaluated, allow us to correct the measured intensity

thereby obtaining |F|, according to the equation below.

hkl

= cL(θ)p(θ)A(θ)E(θ )d(t)m|F

hkl

Some of these factors are angle dependent (vary as a function of θ ). Of

these, Lorentz, L(θ), and polarization, p(θ), corrections are entirely geo-

metric corrections, whilst absorption, A(θ ), and extinction, E(θ), effects

depend on the material content, crystal size and morphology and, in

the case of extinction, the quality of the crystal sample. Sample decay,

d(t), may occur as a function of time. Multiplicity (m) is relevant only to

powder diffraction and may occur if the crystal symmetry of a material

dictates that certain hkl reﬂections must overlap at a given value of θ.

c is simply a constant used for scaling.

Lorentz correction

A Lorentz correction accounts for the fact that the diffraction from some

lattice planes is measured for a longer time than for others as a result of

the way in which 2θ sweeps through reciprocal space.

The Ewald sphere can be used to visualize this: some reﬂections will

intercept the surface of the Ewald sphere at a more oblique angle than

others, according to the way that the crystal lattice rotates relative to

the detector (2θ). The more obliquely a reﬂection intercepts the Ewald

sphere surface, the longer the condition of diffraction is met for that

reﬂection.

Polarization correction

The polarization correction accounts for the partial polarization of both

the incident X-ray beam by the monochromator and that invoked dur-

ing diffraction within the sample. In the latter case, the amount of

70 Background theory for data collection

polarization is dependent on the value of 2θ and is given by P =

(1 + cos

2θ)/2, whereas in the former case, the extent of polarization

depends speciﬁcally on the orientation of the monochromator relative

to the equatorial plane of the diffractometer and the physical nature of

the monochromator crystal.

Absorption correction

A sample can absorb rather than diffract some of the X-ray beam. The

level of absorbance, at a given X-ray wavelength, will depend on the

absorption coefﬁcient, μ, of a sample, which depends in turn on its

elemental make-up (heavier elements generally absorb more), and the

path length of X-rays through a crystal, t, according to the equation,

= I

exp(−μt). Absorption is also dependent upon the wavelength of

the X-ray source: the longer the wavelength, the greater generally the

absorption coefﬁcient for a given sample.

Extinction correction

An X-ray beam can be diffracted by one lattice plane in a crystal, and

then subsequently scatter off another, in a different part of the crystal.

This effect is known as extinction and it causes a loss of intensity for a

given reﬂection. There are two forms of extinction: primary extinction,

which occurs within a crystal domain if the domains are sufﬁciently

misoriented relative to others; and secondary extinction, which occurs

between domains if they are well oriented with respect to each other.

Secondary extinction is usually the dominant form of extinction, and it

predominantly affects strong, low-angle reﬂections. These are normally

corrected for approximately by including a single correction factor as

a variable in the structure reﬁnement. Secondary extinction is wave-

length dependent, becoming worsewith copper than with molybdenum

radiation.

Decay correction

A crystal may degrade over the time of data collection, for example due

to X-ray irradiation damage, chemical reaction of the crystal with air,

moisture or light exposure. In such cases, the expected X-ray intensity

for a given hkl reﬂection decreases over time. Corrections for progres-

sive decay of this type may be undertaken by linear or polynomial curve

ﬁtting of certain reﬂections. This said, it is worth mentioning that with

fast data-collection times made possible by recent area-detector technol-

ogy and increasingly available cryogenic sample-cooling possibilities,

crystal decay is quite rare nowadays.

Apparent crystal decay can also occur if the crystal moves in the X-ray

beam during data collection. One can often correct for such movement

in a similar way.

5.7 Extracting data intensities: data integration and reduction 71

Multiplicity

All lattice planes diffracting at the same Bragg angle will be superim-

posed in a powder X-ray diffraction pattern. This occurs, for example,

in a cubic lattice, d

h00

= d

h00

= d

0k0

= d

0k0

= d

00l

= d

00l

, therefore

multiplicity is 6 in this case.

Other corrections

Sometimes other effects may need to be accounted for. Particularly

noteworthy are thermal diffuse scattering effects and possible varia-

tions in incident X-ray beam intensity (particularly important in some

synchrotron-based X-ray diffraction experiments).

Completion of data-collection procedures

Onceallof these correctionshave been applied to the measuredintensity,

hkl

|can be evaluated for each reﬂection in the dataset. Data reduction is

then complete: the list of resulting h, k, l, and |F| (or |F|

) values is ready

for space group determination, structure solution and onward conver-

sion into a real-space electron-density model of the crystal structure, via

the Fourier transform calculation.

References

Clegg, W. (1984). J. Appl. Crystallogr. 17, 334–336.

Giacovazzo, C. (ed.) (1992). Fundamentals of Crystallography, Oxford

University Press, Oxford, UK, p. 66.

Hornstra, J. and Vossers, H. (1974). Philips Tech. Rundschau 33, 65–78.

Kabsch, W. (1988). J. Appl. Crystallogr. 21, 916–924.

Kabsch, W. (1993). J. Appl. Crystallogr. 26, 795–800.

Proffen, T. R. and Neder, R. B. (2008a). http://www.lks.physik.uni-

erlangen.de/diffraction/iinter_bragg.html

Proffen, T. R. and Neder, R. B. (2008b). http://www.lks.physik.uni-

erlangen.de/diffraction/ibasic_d.html

Sparks, R. A. (1976). Crystallographic Computing Techniques, ed. F. R.

Ahmed. Munskgaard, Copenhagen, pp. 452–467.

Sparks, R. A. (1982). Computational Crystallography, ed. D. Sayre.

Clarendon Press, Oxford, pp. 1–18.