Blake A.J.(ed.) Crystal Structure Analysis

Подождите немного. Документ загружается.

This page intentionally left blank

Practical aspects of

data processing

Alexander Blake

7.1 Data reduction and correction

Once the frameset has been acquired as described in the previous

chapter, integrated intensities must be extracted from the raw frames, a

process that is computationally intensive and impossible without access

to a sufﬁciently precise orientation matrix. While the matrix found from

the initial indexing may be adequate, and it may even be possible to ini-

tiate data reduction to run in parallel with the acquisition of the frames,

this is not always the case and the safest procedure is to harvest reﬂec-

tionsfromtheentiredataset, re-index(to check the unit cell)andre-reﬁne

the matrix using this longer list. Integration software uses the orienta-

tion matrix to determine the reﬂection positions, and the estimation of

intensities can exploit the three-dimensional information available for

each reﬂection through some form of proﬁle ﬁtting. There may also be

facilities for updating and reﬁning the orientation matrix during the

integration process, to allow for uncertainties or gradual changes in the

crystal orientation, but if a high-quality matrix can be determined that

is valid for all frames it is best to use that.

An integration program will also require the relevant calibration and

correction ﬁles in order to apply any corrections (see previous chapter)

that were not applied to the frames as they were being collected.

A typical integration method is that developed by Kabsch (1988).

Reﬂection spot shapes are determined for different regions on the face

of the detector. These model shapes are then used for determining the

area of integration for each reﬂection. The model proﬁle shapes are also

used to calculate correlation coefﬁcients that can be used to reject data

and to ﬁt proﬁles to weak reﬂections.

7.2 Integration input and output

Important input parameters include the reﬂection widths, which may

be reﬁned or ﬁxed. In both cases trial integration runs can be used to

94 Practical aspects of data processing

Input file contains 5746 reflections for this component

Maximum allowed reflections = 25000

Wavelength, relative uncertainty: 0.7107300, 0.0000089

Orientation ('UB') matrix:

0.0375682 –0.0244249 0.0626351

–0.0522494 0.0170492 0.0547843

–0.0979531 –0.0184620 –0.0322734

a b c Alpha

8.8205 28.535 11.582 90.000

Beta

104.686

Gamma

90.000

Vo l

2820.0

0.0009 0.003 0.002 0.000 0.002 0.000 0.9

Standard uncertainties:

Range of reflections used:

Worst res Best res Min 2Theta Max 2Theta

8.8119 0.7685 4.622 55.084

Crystal system constraint: monoclinic b-uniqu

Fig. 7.1 Output from a constrained unit cell reﬁnement.

obtain reasonable initial values. It may be better to err on the wide side

but if the width is too great the integration boxes of neighbouring reﬂec-

tions will overlap andproduceincorrect intensities. Once theintegration

program is running, it should produce some form of diagnostic output:

examination of this (usually with the aid of a manual or other docu-

mentation) provides an indication of how the integration is proceeding.

However, the volume of the raw output can be daunting, and if effec-

tive visualization tools arenot available many users will only referto the

output if they subsequently encounter problems. Users are more likely

to notice and act on the information if it is presented in an accessible

graphical form.

A suitably constrained unit cell reﬁnement (Fig. 7.1) should be car-

ried out, either as part of the data reduction or separately, and should

include a high proportion of the signiﬁcant reﬂections (some software

uses all reﬂections). Although the absolute number of reﬂections is

always high, there may be examples where unit cells reﬁned against

a small proportion of the total data should be regarded with caution.

7.3 Corrections

A description of the required corrections to integrated data appears

in Chapter 5 and these are applied during the integration procedure.

Other possible corrections: (a) Extinc-

tion predominantly affects strong, low-

angle reﬂections and is normally corrected

for approximately by reﬁning a single

correction factor during structure reﬁne-

ment. Secondary extinction is wavelength

dependent, being worse with copper than

with molybdenum radiation. (b) Thermal

diffuse scattering (TDS) can artiﬁcially

enhance the intensity of some high-angle

reﬂections. The fact that TDS decreases

with temperature provides yet another

incentive to collect low-temperature data.

likely to occur if a prominent lattice vec-

tor is aligned with the rotation axis. They

are most obvious where they cause signif-

icant intensity to appear at the position of

a systematic absence. If their signiﬁcance

is not noted they can cause problems with

space group determination, especially if

they affect screw-axis absences. They can

also be recognized by their anomalously

narrow reﬂection proﬁles. (d) Some data-

reduction programs will attempt to com-

pensate for the effects of crystals that are

larger than the X-ray beam. This does not

appear to be problematic for crystals con-

taining light elements, but in other cases

you should avoid this situation rather than

trying to correct for it.

Lorentz and polarization factors (which are instrument speciﬁc) must

be accounted for in all diffractometer measurements. There are vari-

ous methods available for absorptioncorrections.Numerical corrections

can be made on the basis of indexed faces, but routines that exploit

the redundancy present in the data are more widely used (Blessing,

1995; Sheldrick, 1996–2008). Note that redundancy is often rather low

7.5 A typical experiment? 95

for triclinic crystals, and in such cases the corrections need to be assessed

particularly carefully. Alternatively, empirical corrections are always

available if allelse fails. Therange of correction factors output may differ

signiﬁcantly from the range predicted from the cell contents and crystal

dimensions, due in part to the fact that the corrections can encompass

systematic effects other than absorption.

7.4 Output

Part of the output from the data-reduction routine usually includes

analyses of data-signiﬁcance (I/σ ratios as a function of Bragg angle

and other variables), data coverage, and redundancy and consistency

amongequivalentdata under any assumed diffractionsymmetry. Exam-

ination of any such output is strongly recommended: it might cause

you to question your assumptions about the diffraction symmetry, the

validity of the orientation matrix, the quality of the crystal or the com-

pleteness or resolution of your data. You may decide that you need to

re-process the frames. In the most serious cases, and if the crystal is for-

tunately still on the diffractometer, you may even decide that you would

feel safer collecting some more data. However, in most cases there will

be no signiﬁcant problems, and the dataset is available for structure

solution.

7.5 A typical experiment?

The level of detail given in the previous sections may have obscured

a key feature of CCD-based diffractometers, namely their simplicity of

use: below is an outline of an experiment where no particular prob-

lems are encountered. The times shown in brackets for each part of the

procedure are very approximate.

1. Mount, orient and optically centre the crystal (1 minute).

2. Assess crystal quality using still or limited-oscillation exposures

(1 minute).

3. Collect some frames and harvest reﬂections for indexing (several

minutes).

4. Index, reﬁne orientation matrix and determine Bravais lattice

(1 minute).

5. Check whether the unit cell is known and whether its volume is

sensible (1 minute).

6. Survey frames visually to check indexing and assess quality (a few

minutes).

7. Determine the exposure time, frame width and fraction to collect

(1 minute).

8. Record the crystal colour, shape and dimensions (1 minute); index

faces if required (a few minutes).

9. Collect the data (several minutes to hours).

96 Practical aspects of data processing

10. Re-determine the matrix using all available/signiﬁcant reﬂections

(a few minutes).

11. Survey frames visually as a check on the orientation matrix (a few

minutes).

12. Process the data, applying corrections as required (several minutes).

Items 2–6 represent decision points where you have to decide whether

it is worth continuing with the current crystal, and if so how the data

should be collected. If indexing fails at point 4, you might decide to

continue in the hope of succeeding at point 10.

Once a frameset has been processed to yield a ﬁle of reﬂections, you

can analyze these in order to establish the likely space group(s), by

looking at systematic absences and statistical intensity distributions (see

Chapter 4).

7.6 Examples of more problematic cases

As noted above, it is possible to collect a frameset on very unpromising

crystals: with area-detector data the challenge is to process the frames

to give a useable dataset. The difﬁculties most commonly arise from the

inherent quality of the crystal, but others may arise from the techniques

used or from instrumental factors. Any circumstances that cause difﬁ-

culties in deﬁning either a single accurate, valid orientation matrix or

an appropriate description of peak shapes throughout the frameset, are

likely to require some special intervention.

Example 1. A frameset would not index as a whole, despite the

appearance of the frames suggesting no problems.

Solution 1. It proved possible to index each run of frames individu-

ally, giving the same unit cell but slightly different orientation matrices.

No decay was detected and the problem was traced to mechanical slip-

page of the φ circle while it was driving between runs. The data could

be processed successfully by using a separate orientation matrix for

each run.

Example 2. The symptoms were similar to Example 1, but only an

approximate matrix could be deﬁned for each run of frames. Exami-

nation of the frames suggested a systematic drift in the positions of the

reﬂections during each run, relative to their predicted positions. These

symptoms were taken as evidence of a crystal that was not securely

mounted, either because of a poor bond between the crystal and ﬁbre

(or ﬁbre and support), or because of changes occurring in the crystal.

Solution 2. In this case, a failure of the low-temperature system could

be ruled out, and examination of the frames suggested the crystal was

unchanged, pointing to an insecurely mounted crystal. The data were

processed using a separate matrix for each run, but with each matrix

being updated through the run to accommodate the movement of the

7.6 Examples of more problematic cases 97

crystal. If processing had been unsuccessful, it would probably have

been necessary to remount the crystal more securely and recollect all

the frames.

Example 3. A crystal was coated in microcrystalline material that

proved impossible to remove without damaging the crystal, and this

contributed a pervasive background of weak reﬂections in the diffrac-

tion pattern.

Solution 3. It was possible to isolate and integrate the reﬂections from

the main crystal by ﬁrst deriving a matrix based strictly on the strongest

reﬂections,and then extendingthis toinclude thoseof mediumintensity.

Only a small number of intensities in the ﬁnal dataset were signiﬁcantly

affected by overlap from reﬂections from the small crystallites.

Example 4. Acrystal indexed with a primitive unit cell with a moderat-

ely long b-axis of 32 Å, but with broad reﬂections (FWHM=1.2

◦

Solution 4. The combination of long axis and rather broad reﬂections

could lead to reﬂection overlap, so the crystal-to-detector distance was

increased prior to data collection. This allowed larger integration box

sizes to be assessed without causing overlap.

Example 5. Examination of reﬂection proﬁles showed that their widths

varied strongly as a function of goniometer angle. This pronounced

anisomosaicity made it difﬁcultto establish a single integration box size.

Solution 5. It may be possible simply to allow the box size to vary

continuously during the integration, so that it always corresponds to the

characteristics of the local reﬂections. If this option is not available in the

software, or if it does not work satisfactorily, another approach is to use

ﬁxed integration box parameters that are somewhat biased towards the

wider reﬂection proﬁles, followed by correction of the resulting dataset

using multiscan methods (e.g., Blessing, 1995; Sheldrick, 1996–2008).

Example 6. Initial frames indicated serious problems with crystal

quality, including split and poorly shaped reﬂections, as well as the

possibility of more than one component, but it was possible to index the

main component of the pattern.

Solution 6. The sample should be surveyed for better crystals but

if these are not forthcoming it is probably worthwhile collecting the

frames in the hope that the intensities from the main component can

be extracted, giving a starting point for space group determination and

structure solution. Twinning may be present in these circumstances (see

below).

Example 7. Initial indexing yielded a primitive unit cell with one very

long axis (85.6 Å), giving a strong likelihood of severe overlap at the

standard crystal-to-detector distance.

98 Practical aspects of data processing

Solution 7. The overlap problem here can be avoided by increasing the

standard crystal-to-detector distance signiﬁcantly, but this may mean

that the highest achievable 2θ value is rather low. To achieve adequate

resolution, frames will have to be collected at two different detector

theta settings, chosen so that the 2θ ranges overlap. The high-angle data

could be collected using a much longer exposure for each frame. A sim-

ilar strategy of different detector settings and exposure times might

be adopted where diffraction is strong at low angle but then falls off

strongly towards higher angles.

Example 8. The output from the integration program showed good

completeness, a mean redundancy of almost 4.0 and a high propor-

tion of data with I > 2σ(I). There were no indications of problems with

crystal quality, the orientation matrix or the modelling of the reﬂection

proﬁles. However, the internal agreement was terrible, with a merging

R value of 0.66 under monoclinic symmetry. Unsurprisingly, structure

solution failed.

Solution 8. Based on metric considerations alone, the Bravais-lattice

determination had clearly indicated monoclinic C. In the light of the

poor agreement between the intensties under monoclinic symmetry,

this question was revisited and a smaller triclinic P cell chosen. Re-

processing gave a merging R value of 0.10 and the structure was solved

attheﬁrstattempt.Clearly, the crystal possessed higher metric (pseudo)-

symmetry that was inconsistent with the diffraction symmetry.

7.7 Twinning and area-detector data

A much more extensive treatment of twinning appears in Chapter 18,

but some comments regarding non-merohedral twinning are appropri-

ate here. As mentioned above, it is not necessary to have an orientation

matrix before initiating data collection on an area-detector diffractome-

ter,and one consequenceofthis is thatframesetscan sensiblybeacquired

on crystals that (may) have more than one component. The hope is that

it will be possible to identify and index the components later, allowing

the frames to be processed such that the intensity data corresponding

to each component can be extracted.

Atoneextreme,twinning may lead to a complete failureto index using

the normal indexing routines; at the other, it may not be recognized until

problems are encountered with structure solution or reﬁnement; how-

ever, the procedures required to address the problem are identical. It is

obviously helpful to recognize twinning as early as possible: otherwise

you might waste a lot of time, for example by pursuing other solutions to

an unsatisfactory reﬁnement. At the reﬁnement stage, previously unde-

tected non-merohedral twinning may generate a number of symptoms,

including:

• stubbornly high R indices, with no obvious cause such as disorder,

• high-difference Fourier residuals, again with no obvious cause,

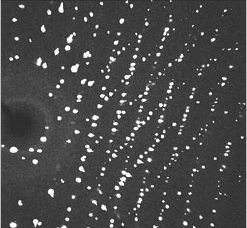
7.8 Some other special cases (in brief) 99

•

individual reﬂections with F(obs)

 F(calc)

, with certainindices

most affected,

• the lowest relative F (calc)

ranges show extreme values for certain

indicators.

Fig. 7.2 A pattern from a crystal suspected

of being a non-merohedral twin.

The ﬁrst indications of non-merohedral twinning may be visible in

the diffraction pattern (Fig. 7.2): deviations from a regular lattice of

well-shaped diffraction maxima may indicate non-merohedral twin-

ning, although they could also indicate other problems. These features

might include adjacent but incompatible (i.e. mutually inclined) recip-

rocal lattice rows; a minority of reﬂections that do not correspond to

the orientation matrix that ﬁts the majority; and reﬂections that show

splitting, overlap, irregular spacing or strange peak shapes.

Although each case has to be assessed individually, the following is a

general procedure for dealing with twinned area-detector data:

• examine frameset for visible indications of twinning,

• use pseudo-precession photographs or other visualization aids,

• identify major twin component, perhaps visually, or using spe-

cial software such as DirAx (Duisenberg, 1992), GEMINI (Bruker,

2004), TwinSolve (Rigaku, 1999–2009), etc.,

• index the major twin component and save reﬁned orientation

matrix 1,

• identify minor twin component,

• index the minor twin component and save reﬁned orientation

matrix 2,

• repeat the last two steps for any further minor components,

• determine and view the relationships between the different

matrices,

• generate predicted patternsusing matrices andcheck these against

frames,

• export orientation matrices for use by your data-reduction

program,

• process the frameset using the orientation matrices,

• output separate or combined datasets for solution and reﬁnement.

7.8 Some other special cases (in brief)

Incommensurate structures. A single unit cell and orientation matrix

are not adequate in such cases because different parts of the structure

exhibit different repeats. The stored frames can be processed to extract

all the required data.

Collection of powder or ﬁbre data. As the whole diffraction pattern

is available, data can be extracted in different ways, for example by

integrating intensity around a powder ring.

Studying phase changes. It is much easier to follow a phase transfor-

mation when the whole diffraction pattern is recorded.

100 Practical aspects of data processing

Diffuse scattering. This can provide information about local structure

(including disorder) in addition to conventional crystallographic data

(e.g., Welberry, 2004).

Exploring lattice defects. Again, the ability to monitor what is happen-

ing between the Bragg positions is valuable.

References

Blessing, R. H. (1995). Acta Crystallogr. 1995, A51, 33–38.

Bruker (2004). GEMINI twinning program suite. Bruker AXS, Madison,

WI, USA.

Duisenberg, A. J. M. (1992). J. Appl. Crystallogr. 25, 92–96.

Kabsch, W. (1988). J. Appl. Crystallogr. 21, 67–71.

Rigaku (1999–2009). TwinSolve. Rigaku/MSC, The Woodlands,

Texas, USA.

Sheldrick, G. M. (1996–2008). SADABS. University of Göttingen,

Germany.

Welberry, T.R. (2004). Diffuse X-Ray Scattering and Models of Disorder,

Oxford University Press/IUCr, Oxford, UK.

Exercises 101

Exercises

1. Measuring a frame for twice the time doubles the

observed intensity I of the reﬂections on that frame.

What is the effect on σ(I) and on I/σ (I)?

2. An area detector with diameter a of 6.0 cm normally sits

at a distance D of 5.0 cm from the crystal. Calculate the

2θ ranges that would be recorded with θ

set at 28.0

◦

if D was increased to (a) 6.0 cm; (b) 7.0 cm; (c) 8.0 cm.

Assuming Mo Kα radiation, at what point should you

consider using two settings for θ

3. A frameset was processed satisfactorily as orthorhom-

bic, except for consistently high values of around

0.25 for the merging R index. Although the result-

ing dataset led to a plausible-looking solution, the

subsequent reﬁnement stalled at R = 0.19. There are

no signiﬁcant absorption effects. Suggest a possible

solution.