Blake A.J.(ed.) Crystal Structure Analysis

Подождите немного. Документ загружается.

42 Space-group determination

Where there is uncertainty about the symmetry, it is best to assume

the lowest possible symmetry during data collection. In structure solu-

tion and reﬁnement, however, the highest possible symmetry should be

taken ﬁrst, with lower symmetry considered only if necessary, avoiding

the danger of missing some symmetry and describing the structure in a

lower-symmetry space group than is correct; in some cases this is a poor

description, but in others it leads to serious errors, particularly where

an inversion centre has been missed.

Some or all of the following stages are involved in working out the

correct space group for a structure, not necessarily in the order given

here. In most of these descriptions, we assume ideal behaviour, and

some of the problems found in real life are considered later.

4.2 Prior knowledge and information other

than from diffraction

Sometimes it is possible to restrict the choice of space groups because

we know something about the material being investigated. One of the

best examples is the study of a compound that is known to be chi-

ral and enantiomerically pure. This expectation may come from the

known synthetic procedure, extraction of a natural product, or phys-

ical measurements. In such a case the individual molecules have no

improper rotation axes (including reﬂection and inversion), and these

symmetry elements must also be absent from the crystal structure as a

whole, because all molecules are of the same hand: any improper rota-

tion requires equal numbers of left and right hands. This immediately

reduces the number of possible point groupsfrom 32 to 11, namely those

that contain only rotation symmetry (or none at all). These point groups

are marked as enantiomorphous in Table 2.5.

Other indications of the absence or presence of certain symmetry

elements may come from the external morphology of well-developed

crystals, or from physical properties such as piezoelectricity, pyroelec-

tricity, or non-linear optical behaviour. These measurements are not

always easy or reliable, however, and are not widely used. By contrast,

simple optical properties should always be examined with a microscope

equipped with crossed polars and a revolving horizontal stage. Apart

from anything else, this gives an indication of whether a crystal is likely

to be single and of reasonable quality and makes it easier to select and

mount a suitable one. Most transparent single crystals under these con-

ditions will appear bright against a dark ﬁeld of view, but will turn dark

quite sharply when rotated into four orientations separated successively

by 90

◦

. This property is called optical extinction (not to be confused

with X-ray extinction, a phenomenon associated with diffraction). Lack

of any well-deﬁned extinction positions usually indicates some kind of

multiplecrystal unsuitable for diffractionstudy, while amorphous mate-

rials like glass appear dark in all orientations. Other conglomerations

of single crystals, including some twins, have regions that extinguish in

4.4 Unit cell contents 43

different orientations instead of a uniform behaviour. The exceptions to

these generalizations are tetragonal, trigonal and hexagonal (‘uniaxial’)

crystals viewed down their unique high-symmetry axis, and cubic crys-

tals viewed in any direction; these are uniformly dark, though uniaxial

crystals should become bright if tipped away from the principal axis.

4.3 Metric symmetry and Laue symmetry

Once the unit cell parameters have been determined, the crystal sys-

tem can usually be selected. It is, however, possible for the unit cell

to show higher metric symmetry than expected, because of fortuitous

equality (within experimental uncertainties) of parameters, or angles

that are close to special values not required by the true symmetry. One

example is a monoclinic cell with a β angle close to 90

◦

. From the unit

cell parameters alone, this could be taken as orthorhombic, since all the

angles are 90

◦

. Similarly, an orthorhombic cell with two almost equal

axis lengths appears to be tetragonal. For this reason it is important to

examine the intensities of groups of reﬂections that should be equiva-

lent for the assumed symmetry. Such reﬂections may be present in the

initial set of data from which the unit cell was determined, or they may

be investigated speciﬁcally at this stage. A ﬁnal conﬁrmation of the true

Laue symmetry (the symmetry of the diffraction pattern with respect to

both geometry and intensities) is best obtained after the complete data

set has been collected.

It is also necessary to examine the intensities of related reﬂections

in order to choose between the two possible Laue classes for each of

the four higher symmetry crystal systems. These account, however, for

only a few per cent of structures of molecular materials, so this will not

need to be done very often. Likewise, primitive trigonal and hexagonal

unit cells can not be distinguished on the basis of their geometry, and

intensities of supposedly equivalent reﬂections must be considered.

Possible problems with this procedure include effects that make

symmetry-equivalent reﬂections have different intensities, particularly

strong absorption for crystals with extreme shapes and/or containing

heavy atoms. Since many absorption correction methods are based on

the measurement of equivalent reﬂections, this can be rather a circular

argument, but in most cases a self-consistent result will be obtained if

there are enough intensity data available to test the various symmetry

possibilities. Final decisions should not be made until a complete data

set has been measured.

4.4 Unit cell contents

Once the unit cell parameters are known, some assessment can be made

of the probable contents of the cell, at least in terms of the number of

atoms and molecules it can accommodate. If the density of the crystals

has been measured, then the mass contents of one unit cell are easily

44 Space-group determination

found from the cell volume (density = mass/volume), and the result

can be compared with the proposed molecular mass for the compound.

D = MZ/N

Here, D is the density, M the molecular mass, Z the number of molecules

in each unit cell, N

Avogadro’s number, and V the unit cell volume. It is

important, of course, to work with consistent units in these calculations!

The usual approach is to calculate Z from the assumed value of M

and the measured cell volume. If all is correct, this should be a whole

number appropriate to the symmetry of the crystal system (common

values are 1 or 2 for triclinic, 2, 4 or 8 for monoclinic, multiples of 4 for

orthorhombic and tetragonal, and numbers with factors of 3 or 6 for

other systems, unless individual molecules themselves can be of high

symmetry and lie on special positions). Failure to obtain a result close

to an integer, or an inappropriate value such as 5 or 7, demonstrates

that the assumed value of the molecular mass is incorrect. This may be

due to the presence of the solvent of crystallization, which has not been

included in the overall molecular mass and leads to too high a value of

Z, or it may be because the compound is not as expected! Sometimes this

simple calculation helps avoid wasting time measuring the diffraction

pattern of a known starting material or uninteresting decomposition

product, but often the experiment proceeds anyway, in order to ﬁnd out

just what the material really is.

If the density has not been measured, a rather more approximate cal-

culation can be made on the basis of an observation that, for a wide

range of organic, organometallic and co-ordination compounds, each

non-hydrogen atom in the unit cell requires an average volume of 18

; in some areas of chemistry a different value may pertain, and this

is a matter of experience. Thus, the number of non-hydrogen atoms per

unit cell can be estimated, and hence the number of molecules Z.

Comparison of the value of Z with the order of a point group (Table 5),

in some cases, provides preliminary information about possible space

groups within those associated with a particular Laue class, and may

indicate that molecules are likely to lie in special positions, because Z

is a fraction of the number of equivalent general positions. The most

common outcome, however, is just an indication that the proposed

chemical formula, possibly with some added solvent of crystallization,

is compatible with the observed unit cell volume and crystal system.

4.5 Systematic absences

The intensity of each reﬂection in the diffraction pattern is due to inter-

ference of the waves scattered from individual atoms in that particular

direction; the greater the degree to which atoms scatter in phase with

each other, the higher is the intensity resulting from superposition of

the waves with crests approximately aligned. The extent to which atoms

4.5 Systematic absences 45

scatter in phase or out of phase relative to each other depends on their

positions in the unit cell. For atoms that are related to each other by

symmetry, the scattering effects are also related. In some cases this

leads to either completely in-phase or strictly out-of-phasecombinations

of waves of equal amplitude; the former gives strong reinforcement,

while the latter leads to a net contribution of zero from these atoms.

At the fundamental level, of course, this is the explanation of the phe-

nomenon of discrete diffraction maxima for X-rays scattered by single

crystals: there is zero intensity in all directions except those given by

the standard diffraction conditions as expressed in the reciprocal lattice

and the Bragg equation, resulting from the pure translation symmetry

of the crystal lattice. Similar effects, in selected parts of the diffrac-

tion pattern, are due to other symmetry elements involving translation

components.

For a lattice described by a primitive unit cell, the diffraction pattern

consists of reﬂections lying at the points of a primitive reciprocal lattice

related in a well-deﬁned way to the crystal lattice. These reﬂections

have a range of intensities. What happens if a centred unit cell (A, B

or C ) is chosen instead of the primitive one, for the same lattice? This

unit cell is twice the size of the original one, so the reciprocal unit cell is

half the size and hence describes a reciprocal lattice with twice as many

points. However, the structure itself has not changed as a result of this

arbitrary choice of axes describing it, and so the diffraction pattern also

remains the same in appearance. Therefore, half of the reciprocal lattice

points for the new description do not lie on observed reﬂections; the

intensities of these predicted ‘reﬂections’ are exactly zero, and they are

called systematic absences. Which reﬂections are systematically absent

is dictated by the choice of axes made in forming the centred unit cell,

i.e. on the nature of the centring (A, B or C).

Each type of unit cell centring (also called lattice centring, though this

is not really correct) has an associated pattern of systematic absences

from which it can be uniquely identiﬁed. These are shown in Table 4.1.

It is from these observed systematic absences in a diffraction pattern

that the cell centring is identiﬁed as part of unit cell and space-group

determination. In this and later tables, in the conditions for observed

intensity, n is any integer (positive, zero or negative), so 2n just means

any even number. Thus, for example, for a reﬂection to be observed for

a body-centred unit cell, the sum of all three indices must be even; if the

sum is odd, the reﬂection has zero intensity.

Centred unit cells produce systematic absences right through the

whole data set; the conditions in Table 4.1 apply to all reﬂections. Sys-

tematic absences in selected parts of the diffraction pattern are observed

when glide planes and screw axes are present in a structure, because

of the translation components of these symmetry elements. If a glide

plane is viewed ‘face on’, perpendicular to its reﬂection, and heights

of atoms above and below this plane are ignored, the unit cell in pro-

jection appears to be centred (for n glide) or halved in one dimension

(for a, b or c glide), so this produces appropriate systematic absences in

46 Space-group determination

Table 4.1. Systematic absences for centred unit cells.

Centring

Points equivalent

to 0,0,0

Condition for

observed intensity

Fraction of

observed data

P none none 1

A 0,

2 k + l = 2n

2,0,

2 h + l = 2n

2,0 h + k = 2n

2 h + k + l = 2n

F 0,

2 and

2,0,

2 h, k , l all even

and

2, 0 or all odd

3 and

3 −h + k + l = 3n

Table 4.2. Systematic absences for glide planes.

Normal to Reﬂections Glide plane Translation Condition for

glide plane affected symbol vector observed intensity

a-axis [100] 0kl b b/2 k = 2n

c c/2 l =2n

n (b+c)/2 k + l =2n

d (b+c)/4 k + l =4n

b-axis [010] h0laa/2 h = 2n

c c/2 l =2n

n (a+c)/2 h + l = 2n

d (a+c)/4 h + l = 4n

c-axis [001] hk0 a a/2 h = 2n

b b/2 k =2n

n (a+b)/2 h + k = 2n

d (a+b)/4 h + k = 4n

10] hhl

c c/2 l = 2n

d (a+b+c)/4 2h + l = 4n

reﬂections whose intensities contain no information about the heights

of atoms perpendicular to the plane. The effect is to remove half the

reﬂections within one two-dimensional section (one sheet or zone)of

the three-dimensional diffraction pattern; in almost all cases observed

in practice these are sets of reﬂections with one index equal to zero. The

complete set of possible systematic absences for glide planes is given in

Table 4.2. The last two rows apply only in the higher-symmetry crys-

tal systems; in the cubic system, the two directions [101] and [011] are

equivalent to [110] and give similar effects.

A similar argument applies for screw axes. In this case, systematic

absences occur for just one row of reﬂections, usually with two indices

equal to zero. Table 4.3 gives the possibilities for screw axes parallel to

each of the unit cell axes (there are other possible directions in higher-

symmetry systems). The recognition of a screw axis from systematic

4.6 The statistical distribution of intensities 47

Table 4.3. Systematic absences for screw axes: conditions for observed intensity.

Parallel

Reﬂections

affected

Condition for

or 6

Condition for

or 6

Condition for

or 4

Condition for

or 6

ah00 h = 2nh= 3nh= 4nh= 6n

b 0k0 k = 2nk= 3nk= 4nk= 6n

c 00ll= 2nl= 3nl= 4nl= 6n

absences is based on only a few reﬂections and so is less reliable than

spotting glide planes and centred unit cells.

The presence or absence of pure rotation, improper rotation, pure

reﬂection, and inversion symmetry cannot be detected from systematic

absences, as these symmetry elements have no translation components.

Some space groups can be uniquely determined from the Laue sym-

metry and systematic absences. Fortunately, these include the two

common space groups P2

/c (alternative settings P2

/n and P2

/a by

different choices of cell axes) and P2

as well as several other rea-

sonably common space groups. In other cases two or more space groups

give the same systematic absences and other information is needed in

order to choose among them.

4.6 The statistical distribution of intensities

Although symmetry elements without a translation component do not

cause systematic absences, they do have an effect on the distribution

of intensities, which may be detected by a statistical analysis of how

the intensities are distributed about their mean value. Such tests are

based on a number of assumptions and approximations and must be

used with due caution. At best they indicate only that something is

probably true, not a certainty. In particular, the tests assume an essen-

tially random arrangement of electron density in the unit cell apart

from the symmetry elements being tested, so a structure containing

atoms with widely different numbers of electrons (except for hydrogen

atoms, which contribute only very weakly to X-ray diffraction) or with

non-crystallographic molecular symmetry may lead to either unclear or

incorrect conclusions.

Statistical tests are not made with the intensities themselves, or even

with the amplitudes derived from them. Just as for direct methods of

structure determination, the amplitudes are converted to ‘normalized

amplitudes’, otherwise known as E-values. These represent what the

amplitudes would be for point atoms at rest instead of vibrating atoms

of ﬁnite size. The derivation of E-values from intensities and ampli-

tudes is described in Chapter 10. They are deﬁned in such a way that

the mean value of |E|

is 1 for all data and should also be 1 for subsets

of the data at different values of sinθ . However, the presence or absence

of an inversion centre in the crystal structure affects the distribution of

48 Space-group determination

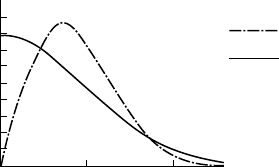
P(E)

⏐

Acentric

Centric

Fig. 4.1 Acentric and centric distributions.

E-values about their mean. With no inversion symmetry, particularly

in the space group P1, E-values do not vary much from their mean,

and the diffraction pattern does not show much variation in intensities.

When there is inversion symmetry present, atoms are in pairs related

by the inversion, and their combined scattering tends to give a greater

proportion of strong reﬂections and weak reﬂections, so that intensities

show more variation overall. The theoretical probability of a reﬂection

having a particular value of |E|, P(E), is quite different in the two cases,

as shown in Fig. 4.1. The two distributions are called acentric and cen-

tric; these are statistical terms describing the distribution of numerical

values, and should not be confused with and used interchangeably with

the terms non-centrosymmetric and centrosymmetric, which apply to

geometrical arrangements, for example of atoms in crystal structures.

The actual distribution of E-values in a particular data set can be

presented in a variety of ways. The most widely used is probably the

simplest: calculation of the mean value of ||E|

−1|for all the data, giving

a single value. This tends to be close to 0.74 for an acentric and 0.97 for a

centric distribution of intensities, so values close to these are indicative

of the probableabsence or presence,respectively, of inversion symmetry.

A similar treatment can be made for rotation axes and mirror planes

by using an appropriate subset of the data and looking for an acentric

or centric distribution. However, with far fewer reﬂections in the set of

data being examined, these are not generally very reliable, and they are

not often used.

4.7 Other points

Even with examination of the Laue symmetry, systematic absences, and

a full statistical analysis of the distribution of intensities, there remain

some space groups that can not be distinguished from each other. These

includeanumberofenantiomorphous pairs, in which one space groupis

the mirror image of the other and the choice between them speciﬁes the

handedness of the structure. They can be distinguished only if the true

handedness is known by other means, or if there is sufﬁcient anomalous

dispersion to show that one ﬁts the diffraction data signiﬁcantly better

4.7 Other points 49

than the other, in which case the ﬁnal choice of space group is not made

until structure reﬁnement is well advanced.

There are also two other pairs of space groups for which the correct

choice can only be made by seeing which leads to successful struc-

ture solution and reﬁnement. These are the orthorhombic pair I222 and

and the cubic pair I23 and I2

3. In both cases the two space

groups have the same symmetry elements, but they are arranged dif-

ferently relative to each other in space. These are unusual and subtle

problems!

Various stages of the space-group determination process may be

adversely affected by problems in the data collection. Poor-quality data

can give unreliable statistical tests, can lead to incorrect or uncertain

decisions about the Laue symmetry, and can make it difﬁcult to work

out the correct systematic absences. In particular, some effects such as

multiple diffraction, the presence of wavelength harmonics, or serious

underestimation of standard uncertainties of intensities can make sys-

tematically absent reﬂections appear to have signiﬁcant and even quite

substantial intensities. In such cases, reliance on fully automatic com-

puter programs is particularly dangerous. Dealing with such problems

may involve careful examination of the originally measured data, and

even a partial or complete repeat of the data collection in some instances.

One complicating factor in space-group determination, and in crystal-

structure determination overall, is the occurrence of pseudo-symmetry.

In some structures there is an approximation to symmetry that is not

exact; for example, two molecules not quite identical and with rela-

tive positions corresponding approximately to centring of the unit cell.

Pseudo-symmetry can lead to various problems and ambiguities, such

as metric symmetry higher than the Laue symmetry, sets of reﬂections

thatwouldhave exactly zerointensity in recognizedsystematicabsences

but are weak rather than completely missing, and mean ||E|

−1|values

intermediate between the centric and acentric ideals. Sometimes this

means the structure can be solved in more than one space group, at

least for the location of some of the atoms, and the pseudo-symmetry is

broken only when further atoms are found.

Some cases of metric symmetry higher than the Laue symmetry (and

some other fortuitous rational geometrical relationships among unit

cell parameters) can lead to unit cells being stacked together in the

wrong orientations during the formation of a crystal, so that the result

is a combination of two different orientations of the same structure in

one apparently single crystal. This means the diffraction patterns of

the two components are superimposed. This effect is called twinning.

Sometimes it is obvious that the observed diffraction pattern can not be

associated with a single-crystal lattice, but in other cases the reﬂections

of the two components coincide. Depending on the precise nature of the

twinning and the space group of the material, this may lead to some

strange patterns of zero intensities, because systematic absences of one

component overlap permitted reﬂections of the other. The resolution of

such problems requires some skill and experience.

50 Space-group determination

There are also cases where a structure can be described either with

disorder in a particular space group or ordered in a lower-symmetry

space group(lacking a symmetry element of inversion, reﬂection or pure

rotation, which are not indicated by systematic absences). The correct

choice is not always easy to make, though it is generally accepted that

the higher symmetry, which usually has fewer parameters, is preferred

unless there are strong indications otherwise. Certainly, if the lower-

symmetry description involves unusualmolecular geometry distortions

or requires extensive use of reﬁnement constraints or restraints, it is

probably wrong.

Finally, it should be noted that the ultimate demonstration of the cor-

rect assignment of a space group is the successful reﬁnement of the

structure with no untoward features. The fact that an initial structure

solution can be obtained in a lower-symmetry space group and not in

a higher one does not prove that the lower symmetry is correct; the

removal of inversion symmetry in particular gives direct methods pro-

grams much more freedom in their calculation of reﬂection phases.

The possible missing symmetry should be looked for carefully in the

structure solution. Various programs exist that can take a partial or com-

pleted structure and examine it for evidence of additional symmetry not

noticed by the experimenter, allowing for a revised assessment and fur-

ther reﬁnement in the higher-symmetry space group. Probably the best

developed and most used of these is PLATON by A. L. Spek of Utrecht

University, The Netherlands. Pseudo-symmetry can also be detected

and explored in this way.

4.8 A brief conducted tour of some entries

in International Tables for

Crystallography, Volume A

The International Tables for Crystallography are important standard refer-

ence works for practising crystallographers. Volume A is all about space

group symmetry – over 800 pages of detailed information including a

variety of representationsand propertiesof each of the 230 space groups,

some of them in alternative axis settings and orientations (for example,

the alternatives P2

/c, P2

/a and P2

/n, and both primitive and obverse-

centred choices for rhombohedral space groups). It should be noted that

there is a much shorter volume of selected space groups available as a

“teaching edition”, with helpful notes, as Brief teaching edition of Volume

A: Space-group symmetry. It currently costs about £17 from the IUCr or

Springer.

Among the information are the following:

1) headings including the space group symbols in both international

and (not very useful) Schoenﬂies notation, the former in conven-

tional short form and also in a full form where this is different;

4.8 A brief conducted tour of some entries in International Tables for Crystallography 51

this full form makes explicit the association of symmetry elements

with particular crystallographic axes;

2) projectionsof the unit cell along differentaxes, with thepositions of

the various symmetry elements, and a separate projection showing

the effect of the symmetry operations on a molecule in a general

position;

3) information about possible choices of origin and the size of the

asymmetric unit in terms of a fraction of the unit cell;

4) a list of the symmetry-related general positions (in a form that is

used by many crystallographic computer programs to represent

the space group symmetry), together with lists of all the special

positions (in which molecules lie on symmetry elements), with

their multiplicities (Z values) and point group symmetry;

5) the systematic absences (actually expressed as positive conditions

for reﬂections to occur, not negative ones for their absence) for the

space group,and also those that arisefor atoms in special positions;

6) various information about the symmetry of two-dimensional

projections and of subgroups and supergroups.

In the lists of general positions, it is quite easy to work out which

are generated by different kinds of symmetry elements. In the three

crystal systems of lowest symmetry (no rotation symmetry higher than

two-fold), the presence of one minus sign before any of x, y and z in a

general position indicates reﬂection; two minus signs indicate rotation,

and three minus signs indicate inversion. Fractions added to x, y or z

area marker of translational components of symmetry elements (centred

unit cells, glide planes and screw axes). If any of x, y or z occurs without

any negative signs in front of it in the list of general positions, this is a

polar axis.