Biringen S., Chow C.-Y. An Introduction to Computational Fluid Mechanics by Example

Подождите немного. Документ загружается.

112 INVISCID FLUID FLOWS

we obtain

m+1, j

= u

m−1, j

for all j (2.11.7)

Under this condition the iterative formula (2.10.13) is modiﬁed at i = m by

m, j +1

= 2u

m−1, j

−u

m, j −1

for j > 2 (2.11.8)

while the starting formula (2.10.18) at the same location becomes

m,2

= f

m−1

+τg

(2.11.9)

Finally, the size of time steps is computed from τ = h/a. This is the time required

for the wave to travel through the distance h. Thus, it takes a time period of 10τ

for the left-propagating wave to reach the closed end starting from its initial

position.

After the solution u

i, j

has been obtained for j ≤ j

max

, the result is plotted

in the form of time-sequential pictures (Time Series 1). The wave shape at one

instant is shown in a frame, with the abscissa representing the spatial coordinate

of the tube and the ordinate the value of u. One frame is plotted every NT time

steps, which is equal to 5 in Program 2.8.

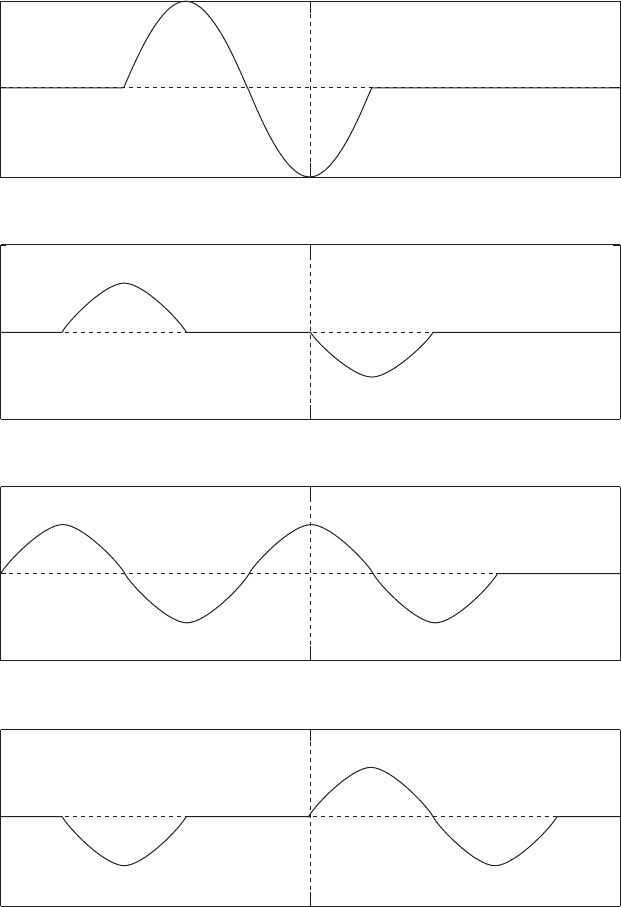
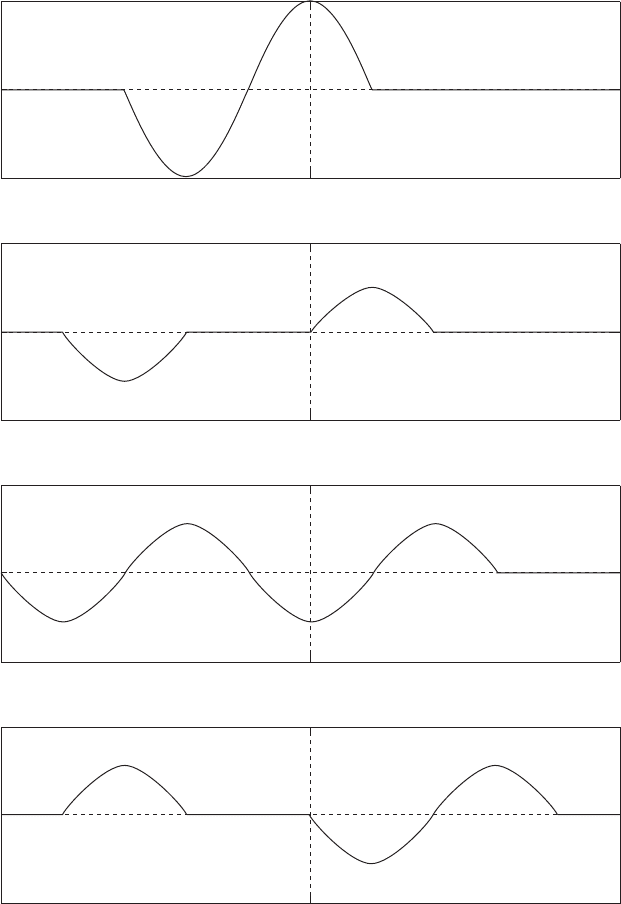
The ﬁrst picture shows the initial state of the wavelet having an amplitude

of 1 m/s and a wavelength of 0.4 m. It decomposes into two identical wavelets

of amplitude 0.5 m/s, but of the original wavelength propagating in opposite

directions. Let us call the one traveling toward the left the L wave and that

toward the right the R wave. At t = 5τ , when each of the two waves have

traveled through a distance equal to one-quarter of the wavelength, the trailing

halves of them coincide to cancel each other so that only the leading halves are

shown. At t = 10τ, these two waves have just come out of each other, but the L

wave starts to impinge on the closed end. Numerical computations show that after

being reﬂected from the rigid wall, the L wave reverses not only its direction of

propagation, but also the sign of u. As can be observed from the ﬁgures plotted

respectively at 10τ and 30τ , the incidental wave is led by positive u,whereas

the reﬂected one is led by negative u. The three ﬁgures in between describe the

interaction of the reﬂected portion with the oncoming part of the L wave.

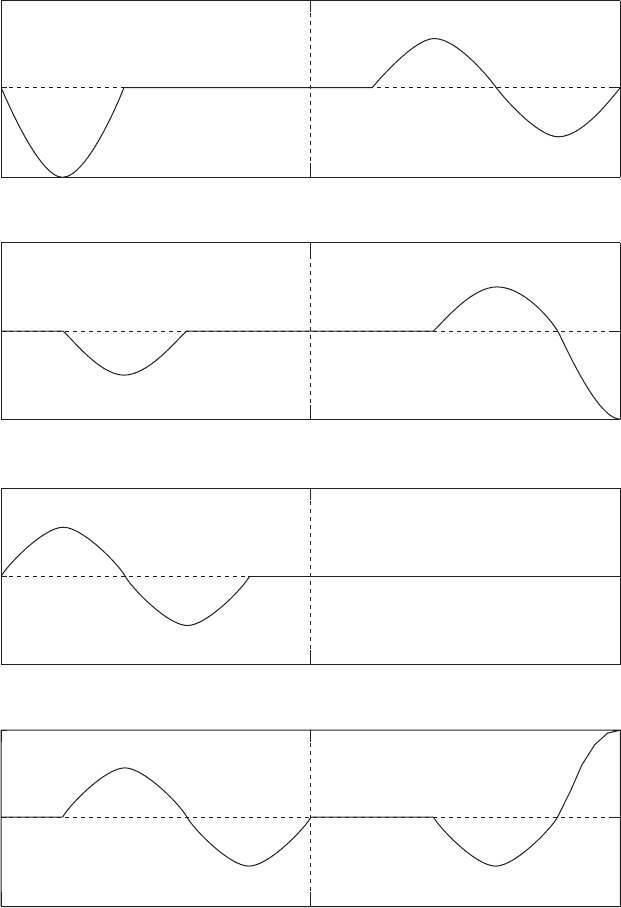
To ﬁnd the effect of the open end on the R wave, let us examine the ﬁgures

plotted between 20τ and 40τ . The conclusion is that after being reﬂected from

an open end, the wave reverses only its direction of propagation, but not the

sign of u. Thus, the reﬂected R wave is still led by negative u, as it was before

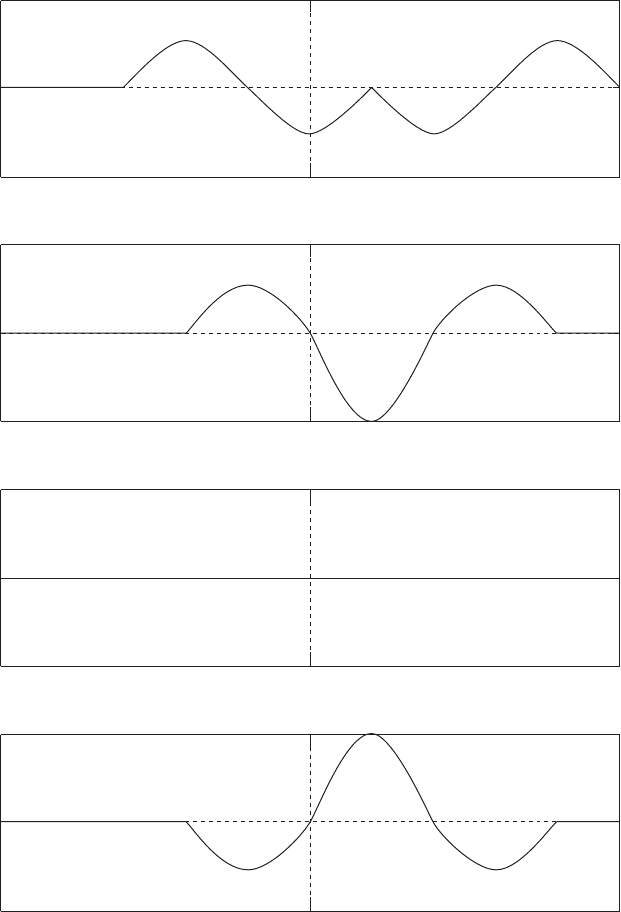
reaching the open end. The four plots after 40τ show the interaction of the two

reﬂected waves when passing each other. At t = 50τ they just cancel each other,

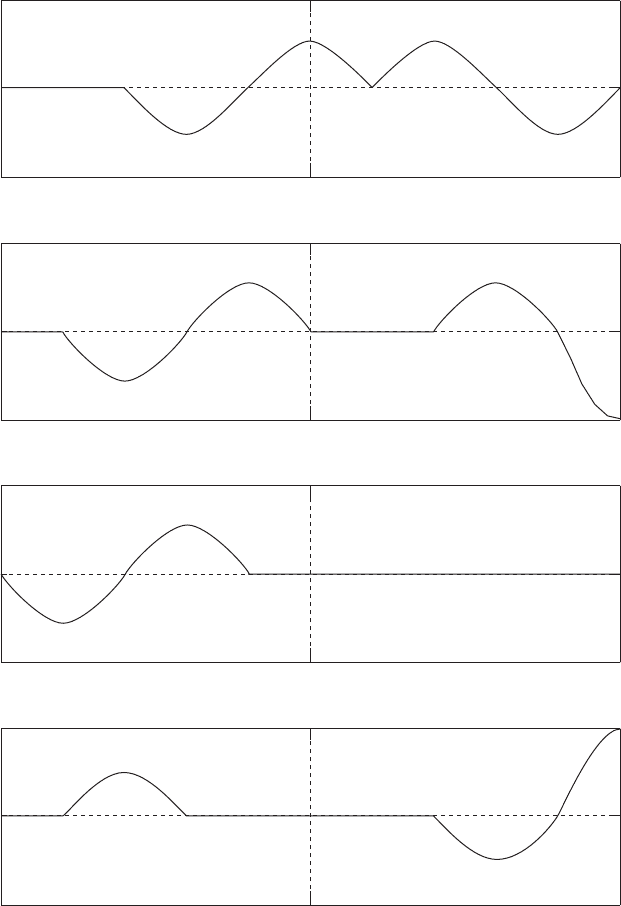
and the tube becomes quiet momentarily. Further reﬂections and interactions are

described in the remaining ﬁgures, and the process may go on forever—in an

inviscid ﬂuid.

PROPAGATION AND REFLECTION OF A SMALL-AMPLITUDE WAVE 113

0 1

−1

Time = 0*tau = 0 seconds

0 1

−1

Time = 5*tau = 0.00029412 seconds

0 1

−1

Time = 10*tau = 0.00058824 seconds

0 1

−1

Time = 15*tau = 0.00088235 seconds

0.5

Time Series 1 Plate 1.

114 INVISCID FLUID FLOWS

0.5 1

−1

Time = 20*tau = 0.0011765 seconds

0 0.5 1

−1

Time = 25*tau = 0.0014706 seconds

0 0.5 1

−1

Time = 30*tau = 0.0017647 seconds

0 0.5 1

−1

Time = 35*tau = 0.0020588 seconds

Time Series 1 Plate 2.

PROPAGATION AND REFLECTION OF A SMALL-AMPLITUDE WAVE 115

0 0.5 1

−1

Time = 40*tau = 0.0023529 seconds

0 0.5 1

−1

Time = 45*tau = 0.0026471 seconds

0 0.5 1

−1

Time = 50*tau = 0.0029412 seconds

0 0.5 1

−1

Time = 55*tau = 0.0032353 seconds

Time Series 1 Plate 3.

116 INVISCID FLUID FLOWS

0 0.5 1

−1

Time = 60*tau = 0.0035294 seconds

0 0.5 1

−1

Time = 65*tau = 0.0038235 seconds

0 0.5 1

−1

Time = 70*tau = 0.0041176 seconds

0 0.5 1

−1

Time = 75*tau = 0.0044118 seconds

Time Series 1 Plate 4.

PROPAGATION AND REFLECTION OF A SMALL-AMPLITUDE WAVE 117

0 0.5 1

−1

Time = 80*tau = 0.0047059 seconds

0.5 1

−1

Time = 85*tau = 0.005 seconds

0 0.5 1

−1

Time = 90*tau = 0.0052941 seconds

0 0.5 1

−1

Time = 95*tau = 0.0055882 seconds

Time Series 1 Plate 5.

118 INVISCID FLUID FLOWS

0 0.5 1

−1

Time = 100*tau = 0.0058824 seconds

0 0.5 1

−1

Time = 105*tau = 0.0061765 seconds

0 0.5 1

−1

Time = 110*tau = 0.0064706 seconds

0 0.5 1

−1

Time = 115*tau = 0.0067647 seconds

Time Series 1 Plate 6.

PROPAGATION AND REFLECTION OF A SMALL-AMPLITUDE WAVE 119

Project for Further Study: When a compressible ﬂuid of density ρ

is dis-

turbed in such a way that its density becomes ρ

+ρ



(x, t),whereρ



 ρ

the density ﬂuctuation, similar to the ﬂuid speed, is also governed by a wave

equation

∂



∂t

= a

∂



∂x

(2.11.10)

This can readily be proved by combining the Euler equation (2.1.5) and the

continuity equation

∂ρ

∂t

+∇ ·(ρV) = 0 (2.11.11)

linearizing them for one-dimensional ﬂow, and then introducing the speed of

sound a =

√

dp/dρ under the isentropic condition. For details consult, for

example, Section 3.4 of Liepmann and Roshko (1957).

Consider a 1-m-long tube of uniform cross section with both ends closed. The

tube is divided into two chambers by a diaphragm at the middle section across

which the densities are slightly different. Suppose ρ



is normalized so that it is 1

at and to the right of the diaphragm, and 0 to the left. At t = 0when∂ρ



/∂t = 0,

the diaphragm is suddenly removed and a wave system is set up in the tube.

Solve this linearized shock tube problem by ﬁnding ρ



(x, t) numerically with the

leapfrog method. Density distributions along the tube at some representative time

levels are to be plotted.

Boundary conditions for density ﬂuctuation in this problem are determined as

follows. At a closed end u vanishes regardless of time; thus, ∂u/∂t = 0there.

This implies that ∂p/∂x = 0 and, therefore, ∂ρ



/∂x = 0 at the closed end by

considering the linearized Euler equation. On the other hand, if there were an

end open to the atmosphere, ρ



should vanish there because the density at that

location is always the same as that outside.

Computer results should show that two waves are generated at the center

after the eruption of the diaphragm: an expansion wave propagating toward the

right and a compression wave propagating toward the left. A wave is classiﬁed

as expansive or compressive, depending on whether the wave is traveling into a

region of higher or lower density. The result should also show that at a rigid wall,

an incidental expansion wave reﬂects as an expansion wave and an incidental

compression wave reﬂects as a compression wave. It can also be shown that the

type of a wave is changed after being reﬂected from an open end.

The conclusion on wave reﬂection from a closed or open end seems to con-

tradict the conclusion obtained from the output of Program 2.8. However, when

the type of a wave is deﬁned in terms of the sign of u in combination with the

direction of propagation, as shown in Fig. 3.3, p. 72 of Liepmann and Roshko

(1957), the contradiction is automatically resolved.

120 INVISCID FLUID FLOWS

2.12 PROPAGATION OF A FINITE-AMPLITUDE WAVE: FORMATION

OF A SHOCK

The numerical solution obtained for the preceding example shows that a sound

wave propagates at a constant velocity without changing its shape. This property

of the wave is the result of linearization of the governing equations, assuming

small perturbations about an equilibrium state of the gas. For a wave whose ampli-

tude is not small, its properties are expected to change (see Zucrow and Hoffman,

1977, Section 19.5). This section offers a numerical study of such a wave.

To derive the equations governing nonlinear wave motions, we rewrite

the continuity equation (2.11.11) and Euler equation (2.1.5) for unsteady

one-dimensional ﬂow:

∂ρ

∂t

∂ρ

∂x

+ρ

∂u

∂x

= 0 (2.12.1)

∂u

∂t

∂u

∂x

∂ρ

∂x

= 0 (2.12.2)

In (2.12.2) the expression a

∂ρ/∂x has been used to replace ∂p/∂x,wherethe

speed of sound, a, is also a function of x and t. We assume that the particle

speed, u, is less than the sonic speed. Under isentropic conditions one of the

three dependent variables, ρ, can be eliminated from the above equations. Let

the subscript 0 indicate the undisturbed conditions and γ be the ratio of speciﬁc

heats of the gas; then





dρ

= γ





γ −1

= a





γ −1

ρ = ρ





2/(γ −1)

(2.12.3)

Substituting (2.12.3) into (2.12.1) and (2.12.2), we obtain

γ −1



∂a

∂t

∂a

∂x



∂u

∂x

= 0

∂u

∂t

∂u

∂x

γ −1

∂a

∂x

= 0

Adding and subtracting, respectively, give the following equations

∂

∂t

+(u +a)

∂

∂x

%

u +

γ −1



= 0 (2.12.4)

PROPAGATION OF A FINITE-AMPLITUDE WAVE: FORMATION OF A SHOCK 121

∂

∂t

+(u −a)

∂

∂x

%

u −

γ −1



= 0 (2.12.5)

Equation (2.12.4) states that the quantity P = u +2a/(γ − 1) is constant along

a curve in the x−t plane. On this curve dP = (∂P/∂t) dt +(∂P/∂x) dx = 0, or,

equivalently,



∂

∂t

∂

∂x



P = 0

Comparing this equation with (2.12.4), we obtain dx/dt = u +a,whichis

the expression for the slope of that curve. Equation (2.12.5) can be similarly

interpreted. Thus, (2.12.4) and (2.12.5) exhibit a salient property that the

quantities P and Q = u − 2a/(γ − 1) are constant on curves that have slopes

dx/dt = u + a and dx/dt = u − a, respectively. These curves are called the

characteristics;P and Q are called the Riemann invariants. Since both u and

a vary with x and t, the characteristics are generally curved lines in the x-t

plane.

The method of characteristics is developed based on the previously mentioned

property. Referring to Fig. 2.12.1, suppose the initial data at t = 0 are given and

the conditions at an arbitrary point C at t

> 0 are to be computed. Through

this point there are two characteristics, one of slope u +a and the other of slope

u −a, which intersect the x axis at points A and B, respectively. Since P

= P

and Q

= Q

or, speciﬁcally,

γ −1

= u

γ −1

−

γ −1

= u

−

γ −1

FIGURE 2.12.1 Method of characteristics.