Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

s16.4

Direct Radiation Between Black Bodies in Vacuo at Different Temperatures

497

Fig.

16.4-1.

Radiation at an angle

from

the normal to the surface into a solid angle

sin

8ddd4.

516.4

DIRECT RADIATION BETWEEN BLACK BODIES

IN VACUO AT DIFFERENT TEMPERATURES

In the preceding sections we have given the Stefan-Boltzmann law, which describes the

total radiant-energy emission from a perfectly black surface. In this section we discuss

the radiant-energy transfer between two black bodies of arbitrary geometry and orienta-

tion. Hence we need to know how the radiant energy emanating from a black body is

distributed with respect to angle. Because black-body radiation is isotropic, the follow-

ing relation, known as Lambert's cosine

law,'

can be deduced:

in which

is the energy emitted per unit area per unit time per unit solid angle in a di-

rection

(see Fig. 16.4-1). The energy emitted through the shaded solid angle is then

sin

de d+

per unit area of black solid surface. Integration of the foregoing expression

for

qfj

over the entire hemisphere gives the known total energy emission:

LZT

qf$

sin

uT4

/021

lo*/'

cos

sin

This justifies the inclusion of the factor of I/T in

Eq.

16.4-1.

We are now in a position to get the net heat transfer rate from body 1 to body 2,

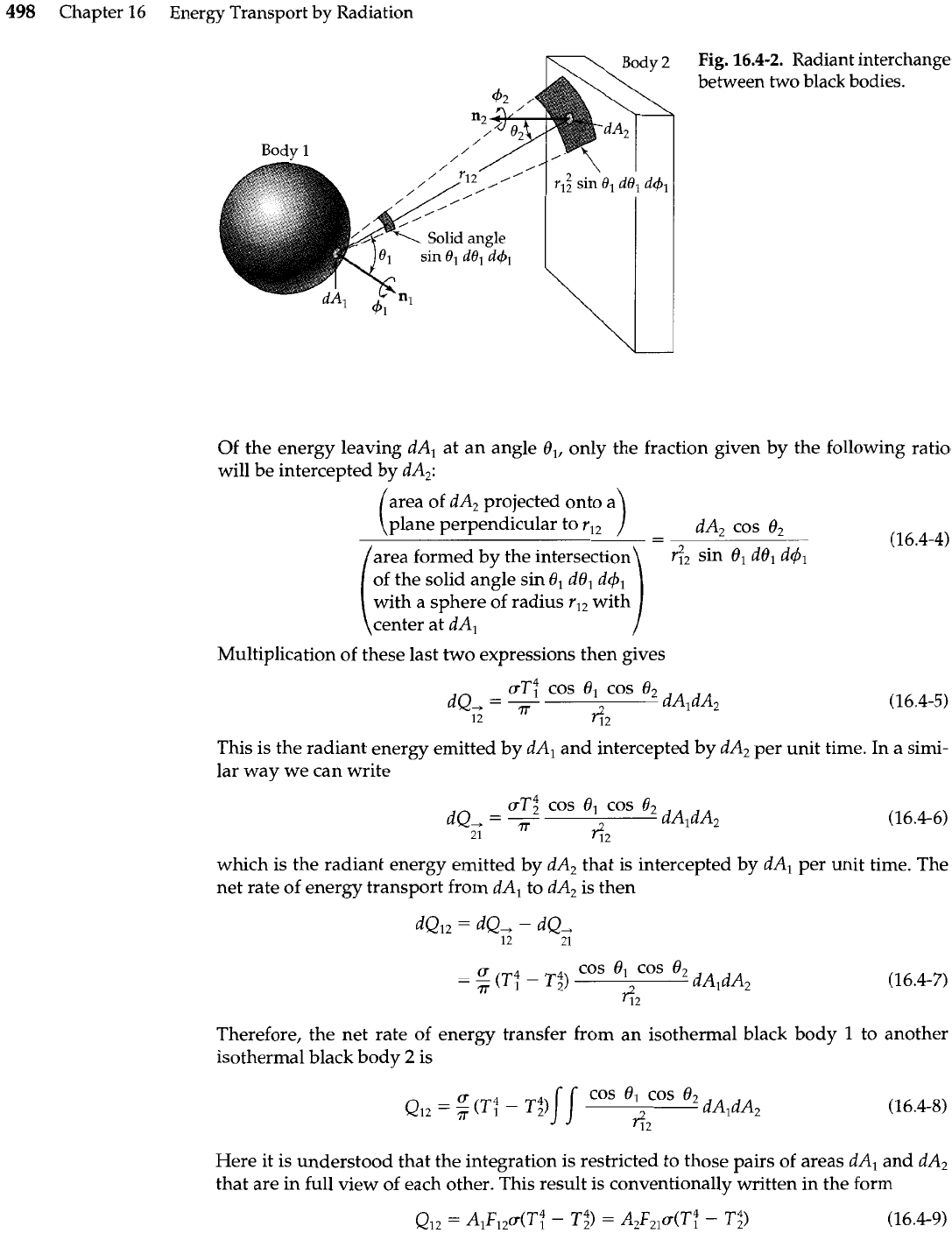
where these are black bodies of any shape and orientation (see Fig. 16.4-2). We do this by

getting the net heat transfer rate between a pair of surface elements

dA,

and

dA,

that can

"see" each other, and then integrating over all such possible pairs

areas. The elements

dAl

and

dA2

are joined by a straight line of length r,,, which makes an angle 8, with the

normal to

dA,

and an angle

with the normal to dA,.

We start by writing an expression for the energy radiated from

dA,

into a solid angle

sin

dB1 d+,

about r,,. We choose this solid angle large enough that

dA2

will lie entirely

within the "beam" (see Fig. 16.4-2). According to Lambert's cosine law, the energy radi-

ated per unit time will be

cos B,)dA, sin

do,

d+,

Lambert,

Photometria,

Augsburg

(1760).

498

Chapter

Energy Transport by Radiation

Fig.

16.4-2.

Radiant interchange

between two black bodies.

Of the energy leaving

dAl

at an angle

O,,

only the fraction given by the following ratio

will be intercepted by

dA,:

area of

dA2

projected onto a

plane perpendicular to

r,,

dA2

cos

(16.4-4)

area formed by the

sin

dBl

d4,

of the solid angle sin

dO,

d+,

with a sphere of radius

r12

with

center at

dA,

Multiplication of these last two expressions then gives

This is the radiant energy emitted by

dA,

and intercepted by

dA,

per unit time. In

simi-

lar way we can write

UT;

cos

dQ,

dAldA2

which is the radiant energy emitted by

dA2

that is intercepted by

dA,

per unit time. The

net rate of energy transport from

dA,

dA2

is then

Therefore, the net rate of energy transfer from an isothermal black body

to another

isothermal black body

Here it is understood that the integration is restricted to those pairs of areas

dA,

and

dA2

that are in full view of each other. This result is conventionally written in the form

g16.4

Direct Radiation Between Black Bodies in Vacuo at Different Temperatures

499

0.1

0.2 0.30.4 0.6 1.0 2 34 6 10-

Dimension ratio

Fig.

16.4-3.

View factors for direct radiation between adjacent rectangles in perpendicular planes

[H.

Hottel, Chapter

McAdams,

Heat

Transmission, McGraw-Hill, New York (1954), p.

681.

where A, and A2 are usually chosen to be the total areas of bodies

and

The dimen-

sionless quantities F,, and F,,, called

view

factors (or angle factors or configuration factors),

are given by

and the two view factors are related by A,F,,

A,F,,. The view factor

F,,

represents the

fraction of radiation leaving body 1 that its directly intercepted by body

The actual calculation of view factors is a difficult problem, except for some very

simple situations. In Fig. 16.4-3 and Fig. 16.4-4 some view factors for direct radiation are

sh~wn.~,~,When such charts are available, the calculations of energy interchanges by Eq.

16.4-9 are easy.

In the above development, we have assumed that Lambert's law and the

Stefan-Boltzmann law may be used to describe the nonequilibrium transport process, in

spite of the fact that they are strictly valid only for radiative equilibrium. The errors thus

introduced do not seem to have been studied thoroughly, but apparently the resulting

formulas give a good quantitative description.

Hottel and

Sarofim,

Radiative Transfer,

McGraw-Hill, New York

(1967).

H.C.

Hottel, Chapter

McAdams,

Heat Transmission,

McGraw-Hill, New York

(1954).

Siege1 and

Howell,

Thermal Radiation Heat Transfer,

3rd edition, Hemisphere Publishing Co.,

New York

(1992).

500

Chapter 16 Energy Transport by Radiation

Diameter or shorter side

Ratio,

Distance between planes

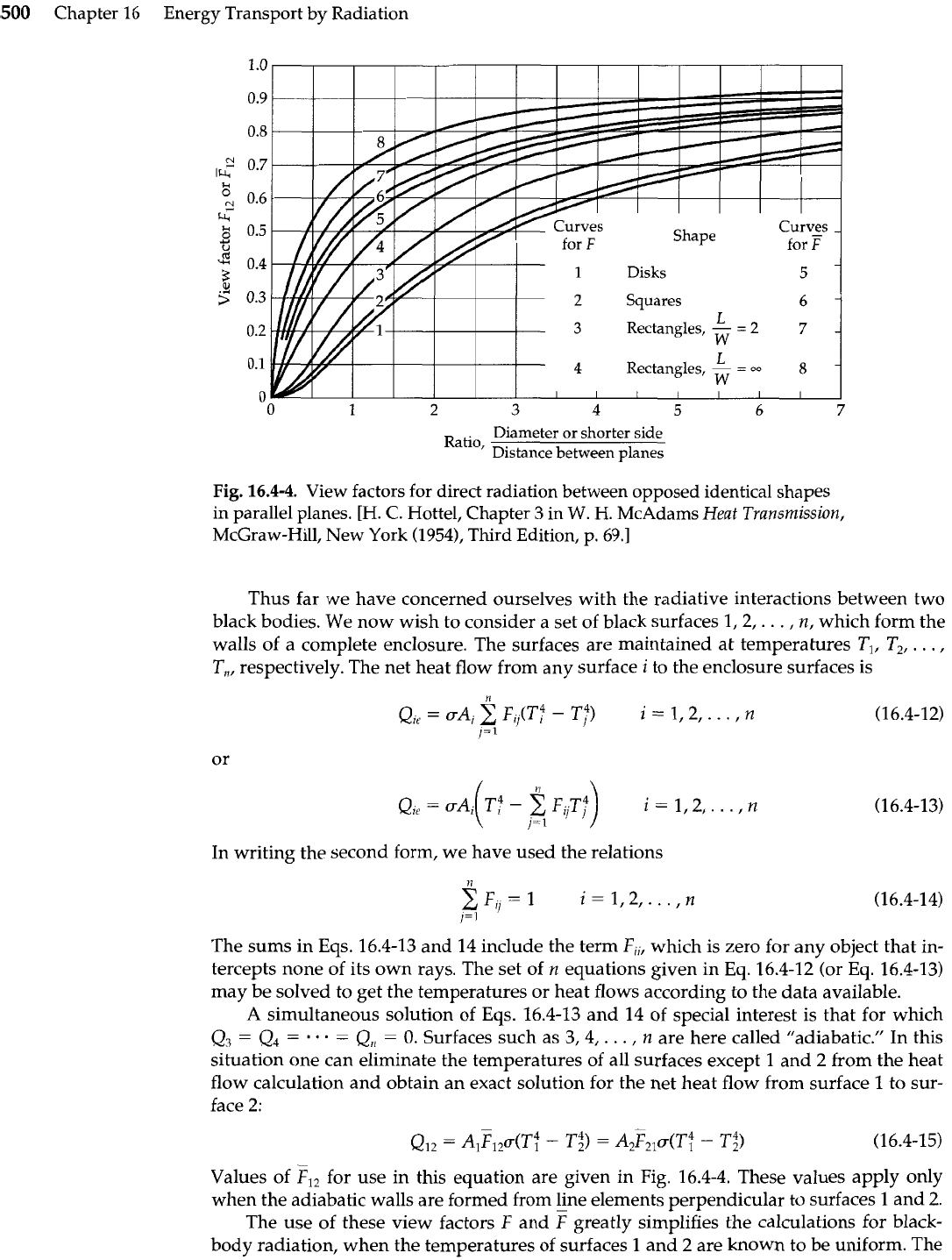
Fig.

16.4-4.

View factors for direct radiation between opposed identical shapes

parallel planes.

[H.

Hottel, Chapter

H. McAdams

Heat

Transmission,

McGraw-Hill, New York (1954), Third Edition, p. 69.1

Thus far we have concerned ourselves with the radiative interactions between two

black bodies. We now wish to consider a set of black surfaces 1,2,

. .

n, which form the

walls of a complete enclosure. The surfaces are maintained at temperatures

TI, T,,

T,,

respectively. The net heat flow from any surface

to the enclosure surfaces is

Q,,

UA,~

F,,(Tf

T$)

1,2,.

(16.4-12)

]=I

In writing the second form, we have used the relations

The sums in Eqs. 16.4-13 and 14 include the term F,,, which is zero for any object that in-

tercepts none of its own rays. The set of

equations given in Eq. 16.4-12 (or Eq. 16.4-13)

may be solved to get the temperatures or heat flows according to the data available.

simultaneous solution of Eqs. 16.4-13 and 14 of special interest is that for which

-Q

4=...=

Surfaces such as 3,4,

are here called "adiabatic." In this

situation one can eliminate the temperatures of all surfaces except 1 and 2 from the heat

flow calculation and obtain an exact solution for the net heat flow from surface

to sur-

face 2:

Values of F,, for use in this equation are given in Fig. 16.4-4. These values apply only

when the adiabatic walls are formed from line elements perpendicular to surfaces 1 and

The use of these view factors

and

greatly simplifies the calculations for black-

body radiation, when the temperatures of surfaces 1 and 2 are known to be uniform. The

516.4

Direct Radiation Between Black Bodies in Vacuo at Different Temperatures

501

Sun

Earth

Fig.

16.4-5.

Estimation of the solar

constant.

92.9

million miles

reader wishing further information on radiative heat exchange in enclosures

referred

to the literat~re.~

The radiant heat flux entering the earth's atmosphere from the sun has been termed the "solar

constant" and is important in solar energy utilization as well as

meteorology. Designate the

Estimation of the

sun as body 1 and the earth as body 2, and use the following data to calculate the solar con-

Solar Constant

stant: Dl

8.60

lo5

miles;

rI2

9.29

lo7

miles;

qfi)

2.0

lo7

Btu/hr. ft2 (from Example

16.3-1).

SOLUTION

In the terminology of

Eq.

16.4-5 and Fig. 16.4-5,

solar constant

cos O1dAl

This is in satisfactory agreement with other estimates that have been made. The treatment of

r:, as a constant in the integrand is permissible here because the distance

r12

varies by less

than 0.5% over the visible surface of the sun. The remaining integral,

cos B,dA,, is the proL

jected area of the sun as seen from the earth, or very nearly .rrJ3:/4.

Two black disks of diameter

are placed directly opposite one another at a distance of 4 ft.

Disk 1 is maintained at 2000°R, and disk

at 1000°R. Calculate the heat flow between the two

Radiant

Heat

Transfer

disks

(a)

when no other surfaces are present, and

(b)

when the two disks are connected by an

Between Disks

adiabatic right-cylindrical black surface.

SOLUTION

(a)

From

Eq.

16.4-9 and curve 1 of Fig. 16.4-4,

Q12

A1F7p(T?

T;)

~(0.06)(0.1712

10-~)[(2000)~

(~ooo)~]

4.83

lo3

Btu/hr

(b)

From Eq. 16.4-15 and curve 5 of Fig. 16.4-4,

502

Chapter

Energy Transport by Radiation

s16.5

RADIATION BETWEEN NONBLACK BODIES

AT DIFFERENT TEMPERATURES

In principle, radiation between nonblack surfaces can be treated by differential analysis

of emitted rays and their successive reflected components. For nearly black surfaces this

is feasible, as only one or two reflections need be considered. For highly reflecting sur-

faces, however, the analysis is complicated, and the distributions of emitted and re-

flected rays with respect to angle and wavelength are not usually known with enough

accuracy to justify a detailed calculation.

reasonably accurate treatment is possible for a small convex surface in a large,

nearly isothermal enclosure (i.e., a "cavity"), such as a steam pipe in a room with walls

at constant temperature. The rate of energy emission from a nonblack surface 1 to the

surrounding enclosure

is given by

and the rate of energy absorption from the surroundings by surface 1 is

Here we have made use of the fact that the radiation impinging on surface 1 is very

nearly cavity radiation or black-body radiation corresponding to temperature T,. Since

A, is convex, it intercepts none of its own rays; hence

F,,

has been set equal to unity. The

net radiation rate from A, to the surroundings is therefore

usu-

In Eq. 16.5-3,

is the value of the emissivity of surface

at TI. The absorptivity

ally

estimated

as the value of

T,.

Next we consider an enclosure formed by

gray, opaque, diffuse-reflecting surfaces

A,, A,, A3,.

A,,

at temperatures TI,

T,,

. . .

T,. Following oppenheiml we define

the

radiosity

for each surface A, as the sum of the fluxes of reflected and emitted radiant

energy from Ai. Then the net radiant flow from Ai to A, is expressed as

that is, by Eq. 16.4-9 with substitution of radiosities

in place of the black-body emissive

powers

ac.

The definition of

gives, for an opaque surface,

in which

is the incident radiant flux on A,. Elimination of

in favor of the net radiant

flux Qi,/Ai from Ai into the enclosure gives

whence

Finally, a steady-state energy balance on each surface gives

Here Q, is the rate of heat addition to surface A, by nonradiative means.

Oppenheim,

Tmns.

ASME,

78,725-735

(1956);

for earlier work, see

Poljak,

Tech.

Phys.

USSR,

1,555-590 (1935).

g16.5 Radiation Between Nonblack Bodies at Different Temperatures

503

Fig.

16.5-1.

Radiation between two infinite, parallel gray

Surface

surfaces.

temperature

with emissivity

Surface

temperature

with emissivity

Radiation potential:

UT~

CTT;

~I~~

I-el

1-ez

Radiation resistance:

-1

elAl

A1F12

e2-42

A2F21

Fig.

16.5-2.

Equivalent cir-

dll

cuit for system shown in

Fig. 16.5-1.

Equations analogous to Eqs. 16.5-4,7, and

arise in the analysis of direct-current cir-

cuits, from Ohm's law of conduction and Kirchhoff's law of charge conservation. Hence

we have the following analogies:

Electrical

Current

Voltage

Resistance

Radiative

This analogy allows easy diagramming of equivalent circuits for visualization of simple

enclosure radiation problems. For example, the system in Fig. 16.5-1 gives the equivalent

circuit shown in Fig. 16.5-2 so that the net radiant heat transfer rate is

The shortcut solution summarized in

Eq.

16.4-15 has been similarly generalized to

non-black-walled enclosures giving

in place of Eq. 16.5-8, for an enclosure with

for

3,.

The result is like

that in Eq. 16.5-9, except that

F1,

must be used instead of

F1,

to include indirect paths

from

to A,, thus giving

larger heat transfer rate.

Develop an expression for the reduction in radiant heat transfer between two infinite parallel

gray planes having the same area, A, when a thin parallel gray sheet of very high thermal

Radiation

Shields

conductivity is placed between them as shown in Fig. 16.5-3.

504

Chapter 16 Energy Transport by Radiation

SOLUTION

Fig.

16.5-3.

Radiation shield.

The radiation rate between planes

and

is given by

since both planes have the same area

and the view factor is unity. Similarly the heat trans-

fer between planes

and 3 is

These last two equations may be combined to eliminate the temperature of the radiation

shield, T,, giving

Then, since

Q,,

Q2,

Q,,, we get

Finally, the ratio of radiant energy transfer with a shield to that without one is

EXAMPLE

16.5-2

Radiation and

Free-

Convection Heat Losses

from a Horizontal Pipe

Predict the total rate of heat loss, by radiation and free convection, from a unit length of hori-

zontal pipe covered with asbestos. The outside diameter of the insulation is 6 in. The outer

surface of the insulation is at 560°R, and the walls and air in the room are at 540°R.

SOLUTION

Let the outer surface of the insulation be surface

and the walls of the room be surface

Then

Eq.

16.15-3 gives

Q12

4Fl2(e1T?

4T;)

(16.5-16)

g16.5 Radiation Between Nonblack Bodies at Different Temperatures

505

Since the pipe surface is convex and completely enclosed by surface

F,,

is unity. From Table

16.2-1, we find e,

0.93 at 560"R and a,

0.93 at 540 R. Substitution of numerical values into

Eq.

16.5-12 then gives for

ft of pipe:

By adding the convection heat loss from Example 14.5-1, we obtain the total heat loss:

Note that in this situation radiation accounts for more than half of the heat loss. If the fluid

were not transparent, the convection and radiation processes would not be independent, and

the convective and radiative contributions could not be added directly.

A body directly exposed to a clear night sky will be cooled below ambient temperature by ra-

diation to outer space. This effect can be used to freeze water in shallow trays well insulated

Combined

Radiation

from the ground. Estimate the maximum air temperature for which freezing is possible, ne-

and

Convection

glecting evaporation.

SOLUTION

As a first approximation, the following assumptions may be made:

All heat received by the water is by free convection from the surrounding air, which is

assumed to be quiescent.

The heat effect of evaporation or condensation of water is not significant.

Steady state has been achieved.

The pan of water is square in cross section.

Back radiation from the atmosphere is neglected.

The maximum permitted air temperature at the water surface is

492"R. The rate of heat

loss

radiation is

in which

is the length of one edge of the pan.

To get the heat gain

convection, we use the relation

in which

is the heat transfer coefficient for free convection. For cooling atmospheric air by

horizontal square facing upward, the heat transfer coefficient is given by2

which h is expressed in Btu/hr. ft2.

and the temperature is given in degrees Rankine.

When the foregoing expressions for heat loss by radiation and heat gain by free convec-

tion are equated, we get

95L2

0.2L2(Tair

492)5/4 (16.5-22)

From this we find that the maximum ambient air temperature is 630°R or 170°F. Except under

desert conditions, back radiation and moisture condensation from the surrounding air greatly

lower the required air temperature.

McAdams,

Chemical Engineers' Handbook

(J.

Perry,

Ed.),

McGraw-Hill, New York

(1950),

3rd

edition,

474.

506

Chapter 16 Energy Transport by Radiation

516.6

RADIANT ENERGY TRANSPORT

ABSORBING MEDIA3

The methods given in the preceding sections are applicable only to materials that are

completely transparent or completely opaque. To describe energy transport in nontrans-

parent media, we write differential equations for the local rate of change of energy as

viewed from both the material and radiation standpoint. That is, we regard a material

medium traversed by electromagnetic radiation as two coexisting "phases": a "material

phase," consisting of all the mass in the system, and a "photon phase," consisting of the

electromagnetic radiation.

In Chapter 11 we have already given an energy balance equation for a system con-

taining no radiation. Here we extend Eq. 11.2-1 for the material phase to take into ac-

count the energy that is being interchanged with the photon phase by emission and

absorption processes:

Here we have introduced

and

which are the local rates of photon emission and ab-

sorption per unit volume, respectively. That is,

represents the energy lost by the mate-

rial phase resulting from the emission of photons by molecules, and

represents the

local gain of energy by the material phase resulting from photon absorption by the mole-

cules (see Fig. 16.6-1). The

in Eq. 16.6-1 is the conduction heat flux given by Fourier's

law.

For the "photon phase," we may write an equation describing the local rate of

change of radiant energy density

dr':

in which

q"'

is the radiant energy flux. This equation may be obtained by writing a radi-

ant energy balance on an element of volume fixed in space. Note that there is no convec-

Photon

L/)

Photon

emission

Fig.

16.6-1.

Volume element over which energy

- - - -

- - -

- - - - -

- - -

- - - -

balances are made; circles represent molecules.

G. C.

Pomraning,

Radiation Hydrodynamics,

Pergamon Press, New York (1973);

Siege1 and

Howell,

Themzal Radiation Heat Transfer,

3rd edition, Hemisphere Publishing Co., New York (1992).