Bird J. Electrical Circuit Theory and Technology
Подождите немного. Документ загружается.

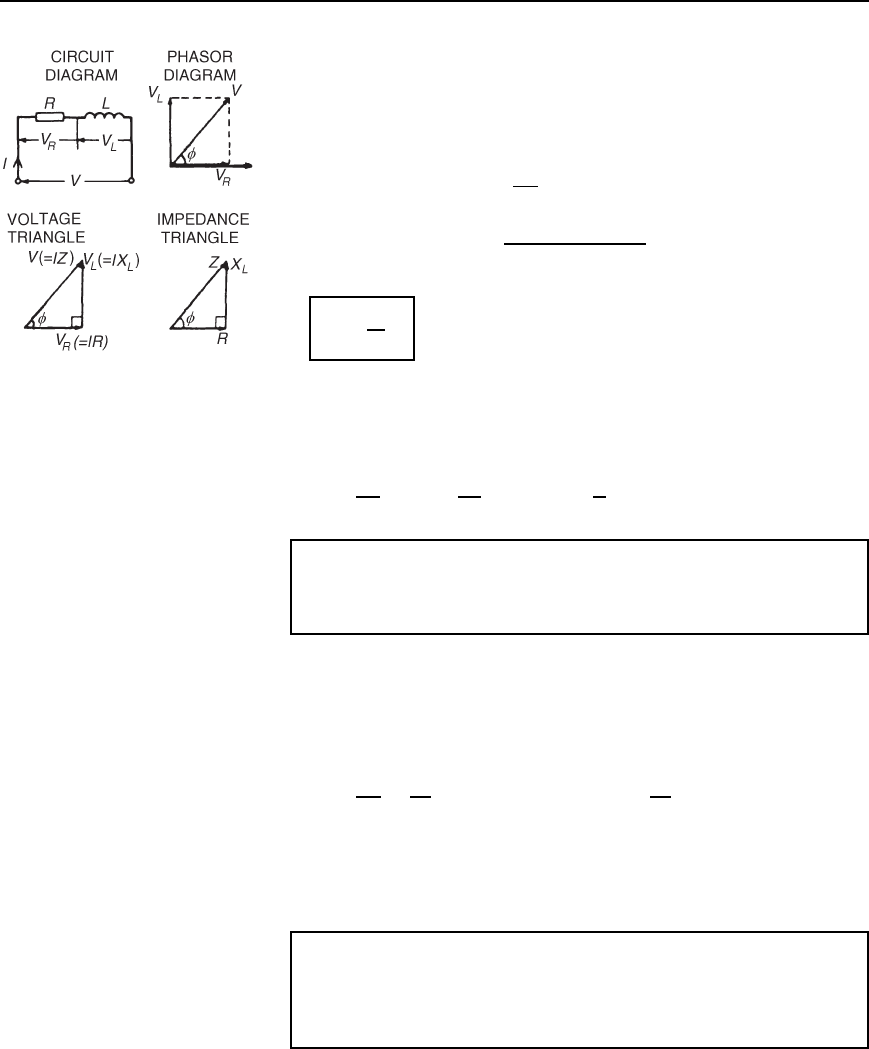
216 Electrical Circuit Theory and Technology
Figure 15.6
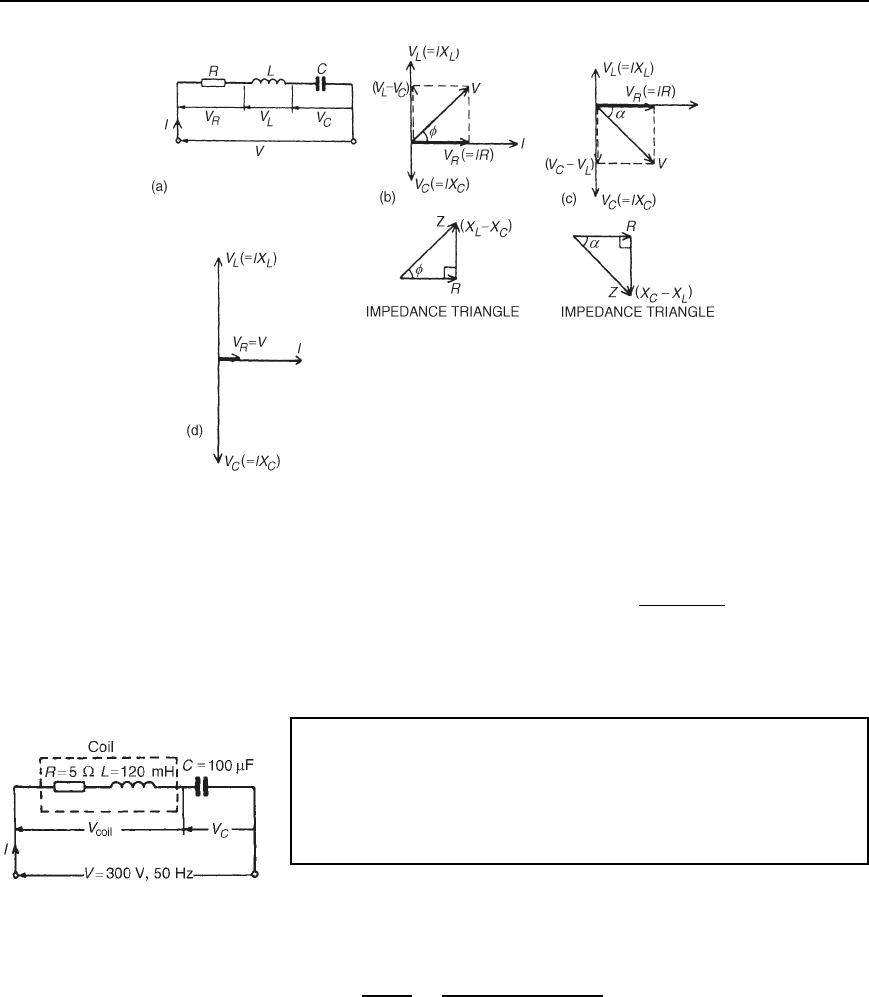
a.c. series circuit the current is common to each component and is thus
taken as the reference phasor.
From the phasor diagram of Figure 15.6, the ‘voltage triangle’ is derived.
For the R –L circuit: V D
V
2
R
C V
2
L
(by Pythagoras’ theorem)
and tan D
V
L
V
R
(by trigonometric ratios)
In an a.c. circuit, the ratio
applied voltage V
current I
is called the impedance Z,
i.e.
Z =
V
I
Z
If each side of the voltage triangle in Figure 15.6 is divided by current I
then the ‘impedance triangle’ is derived.
For the R –L circuit: Z D
R
2
C X
2
L
tan D
X
L
R
, sin D
X
L
Z
and cos D
R
Z
Problem 6. In a series R –L circuit the p.d. across the resistance
R is 12 V and the p.d. across the inductance L is 5 V. Find the
supply voltage and the phase angle between current and voltage.
From the voltage triangle of Figure 15.6,
supply voltage V D
12
2
C 5
2
i.e. V = 13 V
(Note that in a.c. circuits, the supply voltage is not the arithmetic sum of
the p.d’s across components. It is, in fact, the phasor sum.)
tan D
V
L
V
R
D
5
12
, from which D arctan
5
12
D 22.62
°
D 22
°
37
lagging
(‘Lagging’ infers that the current is ‘behind’ the voltage, since phasors
revolve anticlockwise.)
Problem 7. A coil has a resistance of 4 and an inductance
of 9.55 mH. Calculate (a) the reactance, (b) the impedance, and
(c) the current taken from a 240 V, 50 Hz supply. Determine also
the phase angle between the supply voltage and current.
R D 4 ; L D 9.55 mH D 9.55 ð 10
3
H; f D 50 Hz; V D 240 V
(a) Inductive reactance, X
L
D 2fL D 2509.55 ð 10
3
D 3 Z
Single-phase series a.c. circuits 217
(b) Impedance, Z D
R
2
C X
2
L
D
4
2
C 3
2
D 5 Z
(c) Current, I D
V
Z
D
240
5
D 48 A
The circuit and phasor diagrams and the voltage and impedance triangles
are as shown in Figure 15.6.
Sincetan D
X
L
R
,D arctan
X
L
R
D arctan
3
4
D 36.87
°
D 36
°
52
lagging
Problem 8. A coil takes a current of 2 A from a 12 V d.c. supply.
When connected to a 240 V, 50 Hz supply the current is 20 A.
Calculate the resistance, impedance, inductive reactance and induc-
tance of the coil.
Resistance R D
d.c. voltage
d.c. current
D
12
2
D 6
Impedance Z D
a.c. voltage
a.c. current
D
240
20
D 12
Since Z D
R
2
C X
2
L
, inductive reactance, X
L
D
Z
2
R
2
D
12
2
6
2
D 10.39
Since X
L
D 2fL, inductance L D
X
L
2f
D
10.39
250
D 33.1mH
This problem indicates a simple method for finding the inductance of a
coil, i.e. firstly to measure the current when the coil is connected to a
d.c. supply of known voltage, and then to repeat the process with an a.c.
supply.
Problem 9. A coil of inductance 318.3 mH and negligible resis-
tance is connected in series with a 200 resistor to a 240 V, 50 Hz
supply. Calculate (a) the inductive reactance of the coil, (b) the
impedance of the circuit, (c) the current in the circuit, (d) the p.d.
across each component, and (e) the circuit phase angle.
L D 318.3mHD 0.3183 H; R D 200 ; V D 240 V; f D 50 Hz
The circuit diagram is as shown in Figure 15.6.
(a) Inductive reactance X
L
D 2fL D 2500.3183 D 100 Z
(b) Impedance Z D
R
2
C X
2
L
D
[200
2
C 100
2
] D 223.6 Z
218 Electrical Circuit Theory and Technology
(c) Current I D
V
Z
D
240
223.6
D 1.073 A
(d) The p.d. across the coil, V
L
D IX
L
D 1.073 ð 100 D 107.3V
The p.d. across the resistor, V
R
D IR D 1.073 ð 200 D 214.6V
[Check:
V
2
R
C V
2
L
D
[214.6
2
C 107.3
2
] D 240 V, the supply
voltage]
(e) From the impedance triangle, angle D arctan
X
L
R
D arctan
100
200
Hence the phase angle f = 26.57
°
= 26
°
34
lagging
Problem 10. A coil consists of a resistance of 100 and an
inductance of 200 mH. If an alternating voltage,
v, given by v D
200sin500t volts is applied across the coil, calculate (a) the circuit
impedance, (b) the current flowing, (c) the p.d. across the resis-
tance, (d) the p.d. across the inductance and (e) the phase angle
between voltage and current.
Since v D 200sin500t volts then V
m
D 200 V and ω D 2f
D 500 rad/s
Hence rms voltage V D 0.707 ð 200 D 141.4V
Inductive reactance, X
L
D 2fL D ωL D 500 ð 200 ð10
3
D 100
(a) Impedance Z D
R
2
C X
2
L
D
100
2
C 100
2
D 141.4 Z
(b) Current I D
V
Z
D
141.4
141.4
D 1A
(c) p.d. across the resistance V
R
D IR D 1 ð 100 D 100 V
p.d. across the inductance V
L
D IX
L
D 1 ð 100 D 100 V
(e) Phase angle between voltage and current is given by: tan D
X
L
R
from which, D arctan100/100, hence f = 45
°
or
p
4
rads
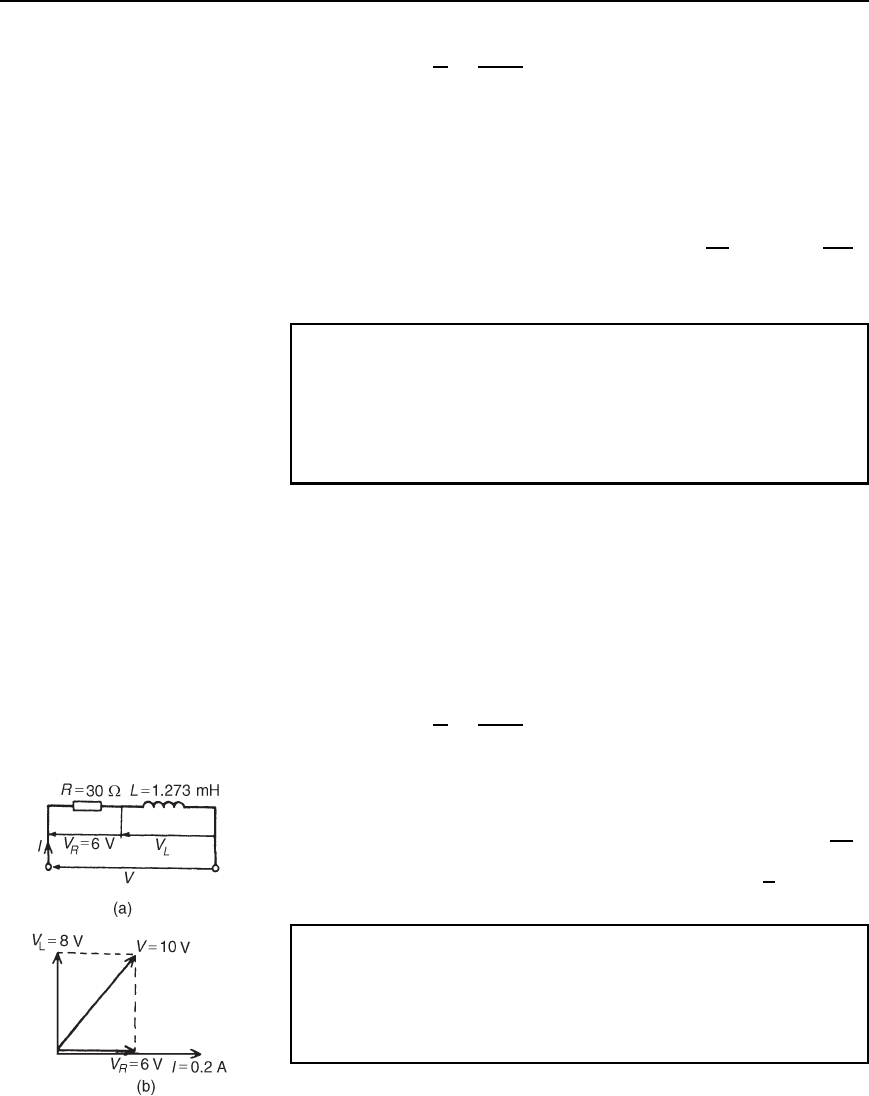
Problem 11. A pure inductance of 1.273 mH is connected in
series with a pure resistance of 30 . If the frequency of the
sinusoidal supply is 5 kHz and the p.d. across the 30 resistor
is 6 V, determine the value of the supply voltage and the voltage
across the 1.273 mH inductance. Draw the phasor diagram.
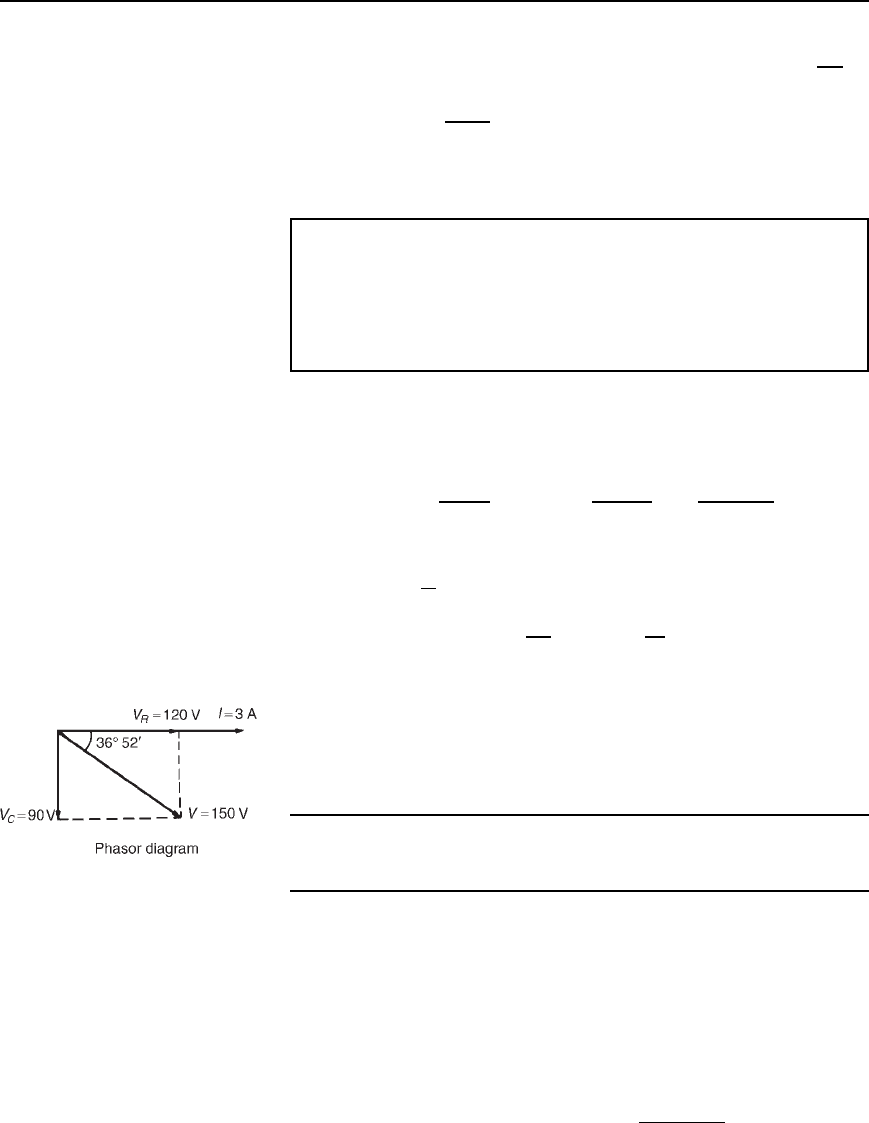
The circuit is shown in Figure 15.7(a).
Supply voltage, V D IZ
Figure 15.7
Single-phase series a.c. circuits 219
Current I D
V
R
R
D
6
30
D 0.20 A
Inductive reactance X
L
D 2fL D 25 ð 10
3
1.273 ð 10
3
D 40
Impedance, Z D
R
2
C X
2
L
D
30
2
C 40
2
D 50
Supply voltage V D IZ D 0.2050 D 10 V
Voltage across the 1.273 mH inductance, V
L
D IX
L
D 0.240 D 8V
The phasor diagram is shown in Figure 15.7(b).
(Note that in a.c. circuits, the supply voltage is not the arithmetic sum of
the p.d.’s across components but the phasor sum)
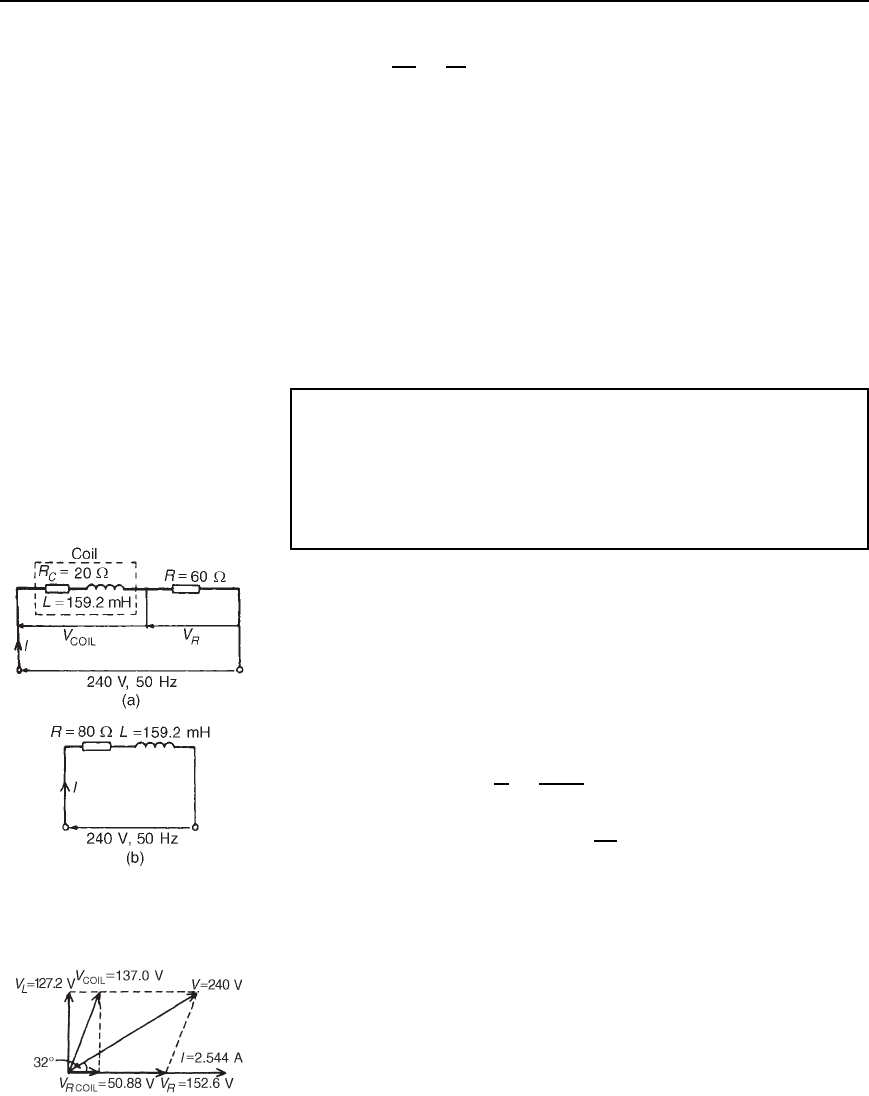
Problem 12. A coil of inductance 159.2 mH and resistance 20
is connected in series with a 60 resistor to a 240 V, 50 Hz supply.
Determine (a) the impedance of the circuit, (b) the current in the
circuit, (c) the circuit phase angle, (d) the p.d. across the 60
resistor and (e) the p.d. across the coil. (f) Draw the circuit phasor
diagram showing all voltages.
The circuit diagram is shown in Figure 15.8(a). When impedances are
connected in series the individual resistances may be added to give
the total circuit resistance. The equivalent circuit is thus shown in
Figure 15.8(b).
Inductive reactance X
L
D 2fL D 250159.2 ð 10
3
D 50
(a) Circuit impedance, Z D
R
2
T
C X
2
L
D
80
2
C 50
2
D 94.34
(b) Circuit current, I D
V
Z
D
240
94.34
D 2.544 A
(c) Circuit phase angle D arctan
X
L
R
D arctan 50/80
D 32
°
lagging
Figure 15.8
From Figure 15.8(a):
(d) V
R
D IR D 2.54460 D 152.6V
(e) V
COIL
D IZ
COIL
, where Z
COIL
D
R
2
C
C X
2
L
D
20
2
C 50
2
D 53.85
Hence V
COIL
D 2.54453.85 D 137.0V
(f) For the phasor diagram, shown in Figure 15.9,
V
L
D IX
L
D 2.54450 D 127.2V
Figure 15.9

220 Electrical Circuit Theory and Technology
V
R COIL
D IR
C
D 2.54420 D 50.88 V
The 240 V supply voltage is the phasor sum of V
COIL
and V
R
Further problems on R–L a.c. series circuits may be found in
Section 15.12, problems 9 to 13, page 234.
15.5 R–C series a.c.
circuit
In an a.c. series circuit containing capacitance C and resistance R, the
applied voltage V is the phasor sum of V
R
and V
C
(see Figure 15.10)
and thus the current I leads the applied voltage V by an angle lying
between 0
°
and 90
°
(depending on the values of V
R
and V
C
), shown as
angle ˛.
From the phasor diagram of Figure 15.10, the ‘voltage triangle’ is
derived. For the R–C circuit:
V D
V
2
R
C V
2
C
(by Pythagoras’ theorem)
and tan ˛ D
V
C
V
R
(by trigonometric ratios)
As stated in Section 15.4, in an a.c. circuit, the ratio
(applied voltage V)/(current I) is called the impedance Z,i.e.Z D
V
I
If each side of the voltage triangle in Figure 15.10 is divided by current
I then the ‘impedance triangle’ is derived.
Figure 15.10
For the R –C circuit: Z D
R
2
C X
2
C
tan˛ D
X
C
R
, sin ˛ D
X
C
Z
and cos ˛ D
R
Z
Problem 13. A resistor of 25 is connected in series with a
capacitor of 45
µF. Calculate (a) the impedance, and (b) the current
taken from a 240 V, 50 Hz supply. Find also the phase angle
between the supply voltage and the current.
R D 25 ; C D 45 µF D 45 ð 10
6
F; V D 240 V; f D 50 Hz
The circuit diagram is as shown in Figure 15.10
Capacitive reactance, X
C
D
1
2fC
D
1
25045 ð 10
6
D 70.74
(a) Impedance Z D
R
2
C X
2
C
D
[25
2
C 70.74
2
] D 75.03 Z
(b) Current I D
V
Z
D
240
75.03
D 3.20 A
Single-phase series a.c. circuits 221
Phase angle between the supply voltage and current, ˛ D arctan
X
C
R
hence ˛ D arctan
70.74
25
D 70.54
°
D 70
°
32
leading
(‘Leading’ infers that the current is ‘ahead’ of the voltage, since phasors
revolve anticlockwise.)
Problem 14. A capacitor C is connected in series with a 40
resistor across a supply of frequency 60 Hz. A current of 3 A
flows and the circuit impedance is 50 . Calculate: (a) the value of
capacitance, C, (b) the supply voltage, (c) the phase angle between
the supply voltage and current, (d) the p.d. across the resistor, and
(e) the p.d. across the capacitor. Draw the phasor diagram.
(a) Impedance Z D
R
2
C X
2
C
Hence X
C
D
Z
2
R
2
D
50
2
40
2
D 30
X
C
D
1
2fC
hence C D
1
2fX
C
D
1
26030
F
D 88.42 mF
(b) Since Z D
V
I
then V D IZ D 350 D 150 V
(c) Phase angle, ˛ D arctan
X
C
R
D arctan
30
40
D 36.87
°
D 36
°
52
leading
(d) P.d. across resistor, V
R
D IR D 340 D 120 V
(e) P.d. across capacitor, V
C
D IX
C
D 330 D 90 V
The phasor diagram is shown in Figure 15.11, where the supply voltage
V is the phasor sum of V
R
and V
C
.
Further problems on R–C a.c. circuits may be found in Section 15.12,
problems 14 to 17, page 235.
Figure 15.11
15.6 R–L–C series a.c.
circuit
In an a.c. series circuit containing resistance R, inductance L and capac-
itance C, the applied voltage V is the phasor sum of V
R
, V
L
and V
C
(see Figure 15.12). V
L
and V
C
are anti-phase, i.e. displaced by 180
°
,and
there are three phasor diagrams possible—each depending on the relative
values of V
L
and V
C
When X
L
> X
C
(Figure 15.12(b) : Z D
[R
2
C X
L
X
C
2
]
and tan D
X
L
X
C
R
222 Electrical Circuit Theory and Technology
Figure 15.12
When X
C
> X
L
(Figure 15.12(c) : Z D
[R
2
C X
C
X
L
2
]
and tan˛ D
X
C
X
L
R
When X
L
= X
C
(Figure 15.12(d)), the applied voltage V and the current
I are in phase. This effect is called series resonance (see Section 15.7)
Problem 15. A coil of resistance 5 and inductance 120 mH in
series with a 100
µF capacitor, is connected to a 300 V, 50 Hz
supply. Calculate (a) the current flowing, (b) the phase difference
between the supply voltage and current, (c) the voltage across the
coil and (d) the voltage across the capacitor.
Figure 15.13
The circuit diagram is shown in Figure 15.13
X
L
D 2fL D 250120 ð 10
3
D 37.70 Z
X
C
D
1
2fC
D
1
250100 ð 10
6
D 31.83 Z
Since X
L
is greater than X
C
the circuit is inductive.
X
L
X
C
D 37.70 31.83 D 5.87

Single-phase series a.c. circuits 223
Figure 15.14
Impedance Z D
[R
2
C X
L
X
C
2
] D
[5
2
C 5.87
2
] D 7.71
(a) Current I D
V
Z
D
300
7.71
D 38.91 A
(b) Phase angle D arctan
X
L
X
C
R
D arctan
5.87
5
D 49.58
°
D 49
°
35
(c) Impedance of coil Z
COIL
D
R
2
C X
2
L
D
[5
2
C 37.70
2
]
D 38.03
Voltage across coil V
COIL
D IZ
COIL
D 38.9138.03 D 1480 V
Phase angle of coil D arctan
X
L
R
D arctan
37.70
5
D 82.45
°
D 82
°
27
0
lagging
(d) Voltage across capacitor V
C
D IX
C
D 38.9131.83 D 1239 V
The phasor diagram is shown in Figure 15.14. The supply voltage V is
the phasor sum of V
COIL
and V
C
Series connected impedances
For series-connected impedances the total circuit impedance can be repre-
sented as a single L –C–R circuit by combining all values of resistance
together, all values of inductance together and all values of capacitance
together,
(remembering that for series connected capacitors
1
C
D
1
C
1
C
1
C
2
C ...).
Figure 15.15
For example, the circuit of Figure 15.15(a) showing three impedances has
an equivalent circuit of Figure 15.15(b).
224 Electrical Circuit Theory and Technology
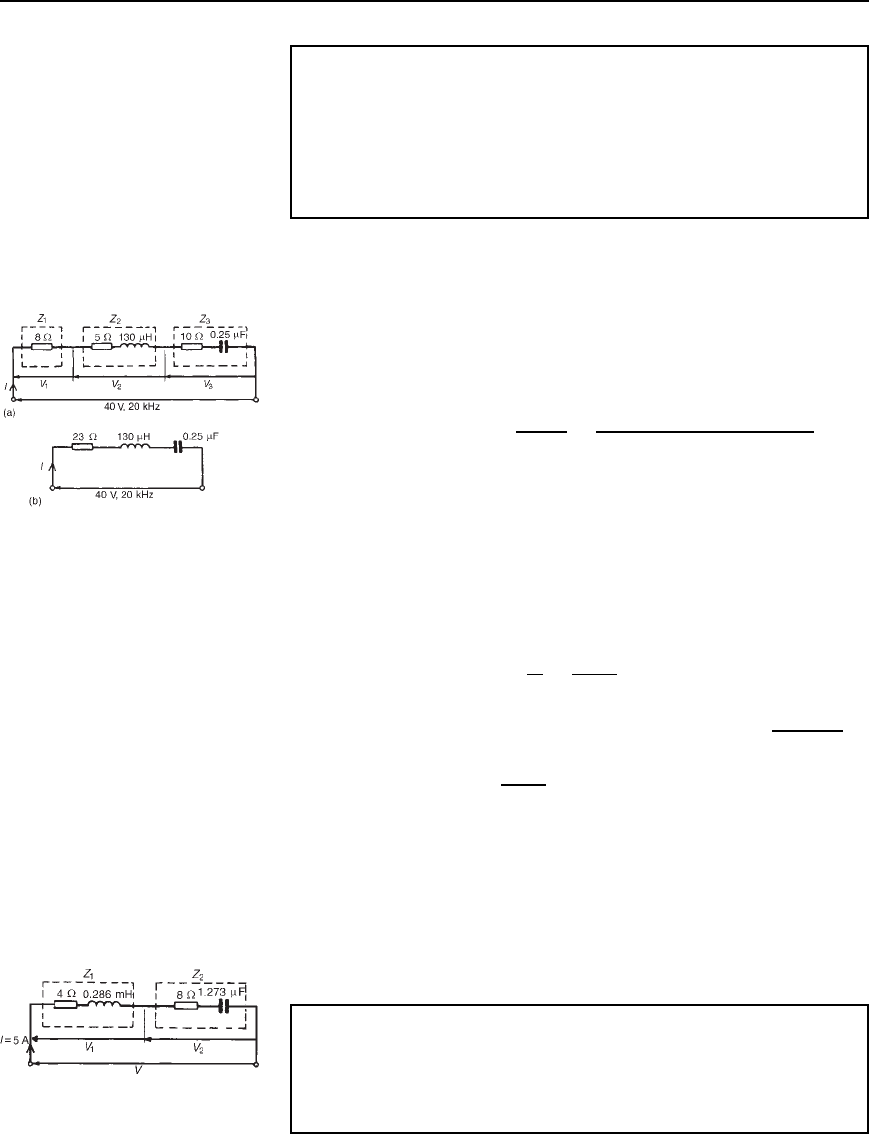
Problem 16. The following three impedances are connected in
series across a 40 V, 20 kHz supply: (i) a resistance of 8 , (ii) a
coil of inductance 130
µH and 5 resistance, and (iii) a 10
resistor in series with a 0.25
µF capacitor. Calculate (a) the circuit
current, (b) the circuit phase angle and (c) the voltage drop across
each impedance.
The circuit diagram is shown in Figure 15.16(a). Since the total circuit
resistance is 8 C 5 C10, i.e. 23 , an equivalent circuit diagram may be
drawn as shown in Figure 15.16(b)
Inductive reactance, X
L
D 2fL D 220 ð 10
3
130 ð 10
6
D 16.34
Capacitive reactance, X
C
D
1
2fC
D
1
220 ð 10
3
0.25 ð 10
6
D 31.83
Since X
C
>X
L
, the circuit is capacitive (see phasor diagram in
Figure 15.12(c)). X
C
X
L
D 31.83 16.34 D 15.49
Figure 15.16
(a) Circuit impedance, Z D
[R
2
C X
C
X
L
2
] D
[23
2
C 15.49
2
]
D 27.73
Circuit current, I D
V
Z
D
40
27.73
D 1.442 A
From Figure 15.12(c), circuit phase angle D arctan
X
C
X
L
R
i.e, D arctan
15.49
23
D 33.96
°
D 33
°
58
leading
(b) From Figure 15.16(a), V
1
D IR
1
D 1.4428 D 11.54 V
V
2
D IZ
2
D I
5
2
C 16.34
2
D 1.44217.09 D 24.64 V
V
3
D IZ
3
D I
10
2
C 31.83
2
D 1.44233.36 D 48.11 V
The 40 V supply voltage is the phasor sum of V
1
, V
2
and V
3
Figure 15.17
Problem 17. Determine the p.d.’s V
1
and V
2
for the circuit shown
in Figure 15.17 if the frequency of the supply is 5 kHz. Draw the
phasor diagram and hence determine the supply voltage V and the
circuit phase angle.
Single-phase series a.c. circuits 225
For impedance Z
1
:
R
1
D 4 and X
L
D 2fL D 25 ð 10
3
0.286 ð 10
3
D 8.985
V
1
D IZ
1
D I
R
2
C X
2
L
D 5
4
2
C 8.985
2
D 49.18 V
Phase angle
1
D arctan
X
L
R
D arctan
8.985
4
D 66
°
0
lagging
For impedance Z
2
:
R
2
D 8 and X
C
D
1
2fC
D
1
25 ð 10
3
1.273 ð 10
6
D 25.0
V
2
D IZ
2
D I
R
2
C X
2
C
D 5
8
2
C 25.0
2
D 131.2V
Phase angle
2
D arctan
X
C
R
D arctan
25.0
8
D 72
°
15
0
leading
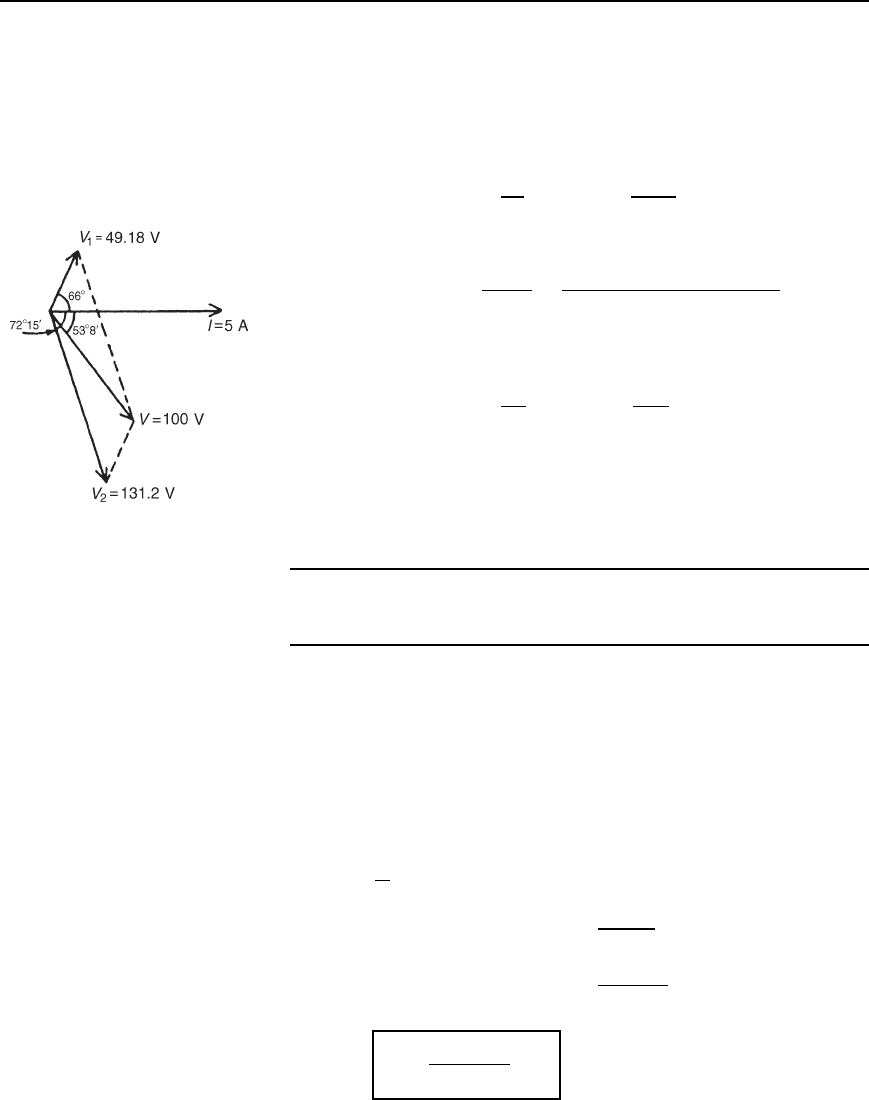
The phasor diagram is shown in Figure 15.18.
The phasor sum of V
1
and V
2
gives the supply voltage V of 100 V at a
phase angle of 53
°
8
leading. These values may be determined by drawing
or by calculation—either by resolving into horizontal and vertical compo-
nents or by the cosine and sine rules.
Figure 15.18
Further problems on R–L–C a.c. circuits may be found in Section 15.12,
problems 18 to 20, page 235.
15.7 Series resonance
As stated in Section 15.6, for an R–L –C series circuit, when X
L
D X
C
(Figure 15.12(d)), the applied voltage V and the current I are in phase.
This effect is called series resonance. At resonance:
(i) V
L
D V
C
(ii) Z D R (i.e. the minimum circuit impedance possible in an L –C–R
circuit)
(iii) I D
V
R
(i.e. the maximum current possible in an L –C–R circuit)
(iv) Since X
L
D X
C
, then 2f
r
L D
1
2f
r
C
from which, f
2
r
D
1
2
2
LC
and,
f
r
=
1
2p
p
.LC/
Hz,
where f
r
is the resonant frequency.
