Bird J. Electrical Circuit Theory and Technology

Подождите немного. Документ загружается.

196 Electrical Circuit Theory and Technology

The average or mean value of a symmetrical alternating quantity,

(such as a sine wave), is the average value measured over a half cycle,

(since over a complete cycle the average value is zero).

Average or mean value

area under the curve

length of base

The area under the curve is found by approximate methods such as the

trapezoidal rule, the mid-ordinate rule or Simpson’s rule. Average values

are represented by V

, I

, etc.

For a sine wave, average value = 0.637 × maximum value

(i.e. 2=p

× maximum value)

The effective value of an alternating current is that current which will

produce the same heating effect as an equivalent direct current. The effec-

tive value is called the root mean square (rms) value and whenever

an alternating quantity is given, it is assumed to be the rms value. For

example, the domestic mains supply in Great Britain is 240 V and is

assumed to mean ‘240 V rms’. The symbols used for rms values are I,

V, E, etc. For a non-sinusoidal waveform as shown in Figure 14.4 the

rms value is given by:

I D





C i

C ...Ci



Figure 14.4

where n is the number of intervals used.

For a sine wave, rms value = 0.707 × maximum value

(i.e. 1=

× maximum value)

Form factor D

rms value

average value

For a sine wave,

form factor = 1.11

Peak factor D

maximum value

rms value

For a sine wave,

peak factor = 1.41

The values of form and peak factors give an indication of the shape of

waveforms.

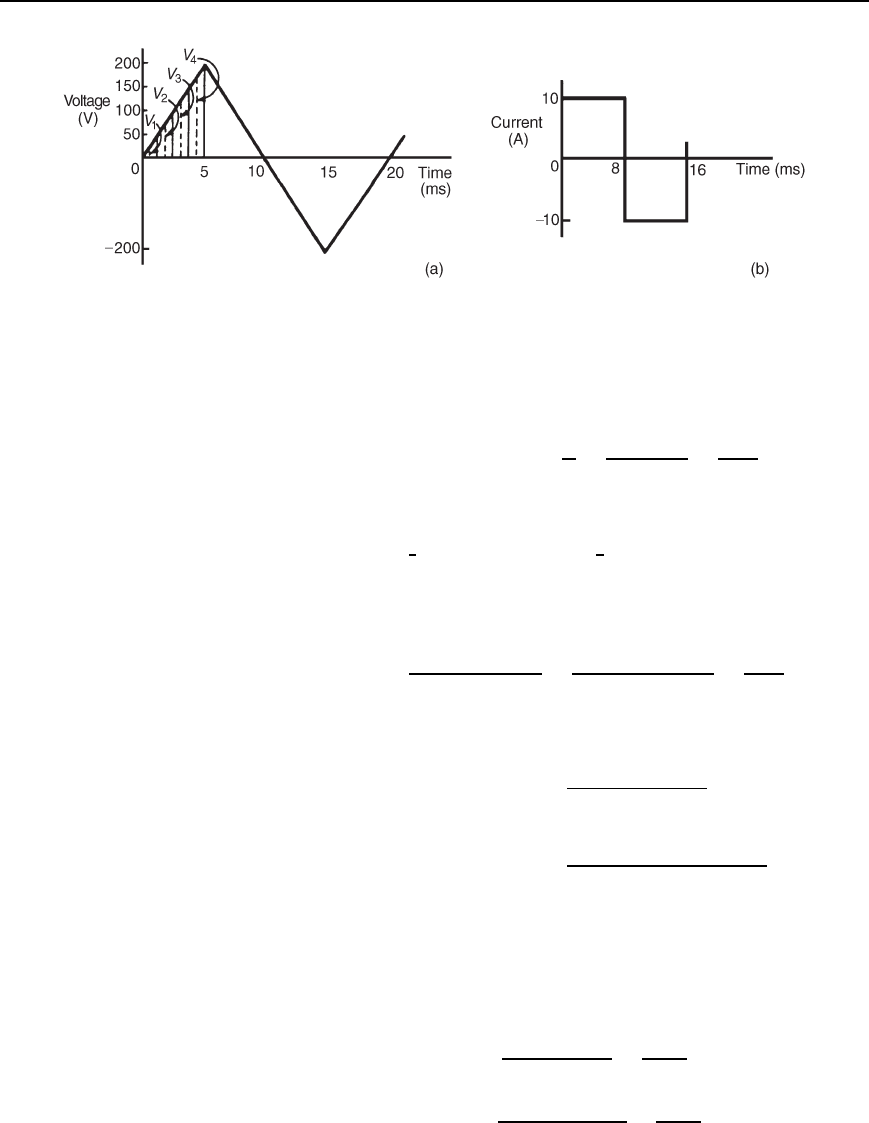
Problem 4. For the periodic waveforms shown in Figure 14.5

determine for each: (i) frequency (ii) average value over half a

cycle (iii) rms value (iv) form factor and (v) peak factor

Alternating voltages and currents 197

Figure 14.5

(a) Triangular waveform (Figure 14.5(a))

(i) Time for 1 complete cycle D 20 ms D periodic time, T

Hence frequency f D

20 ð 10

3

1000

D 50 Hz

(ii) Area under the triangular waveform for a half cycle

ð base ð height D

ð 10 ð 10

3

 ð 200

D 1 volt second

Average value of waveform

area under curve

length of base

1 volt second

10 ð 10

3

second

1000

D 100 V

(iii) In Figure 14.5(a), the ﬁrst 1/4 cycle is divided into 4 intervals.

Thus rms value D





C v







C 75

C 125

C 175



D 114.6V

(Note that the greater the number of intervals chosen, the greater the

accuracy of the result. For example, if twice the number of ordinates

as that chosen above are used, the rms value is found to be 115.6 V)

(iv) Form factor D

rms value

average value

114.6

100

D 1.15

(v) Peak factor D

maximum value

rms value

200

114.6

D 1.75

198 Electrical Circuit Theory and Technology

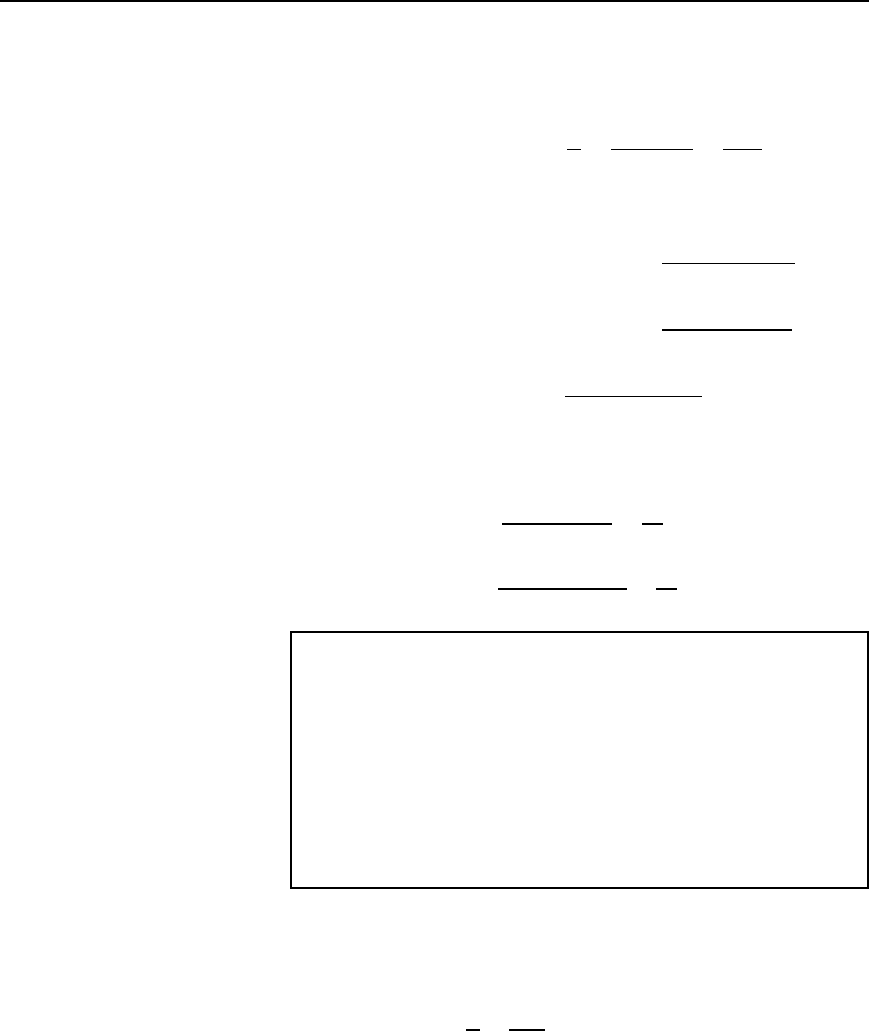
(b) Rectangular waveform (Figure 14.5(b))

(i) Time for 1 complete cycle D 16 ms D periodic time, T

Hence frequency, f D

16 ð 10

3

1000

D 62.5 Hz

(ii) Average value over half a cycle D

area under curve

length of base

10 ð 8 ð 10

3



8 ð 10

3

D 10 A

(iii) The rms value D





C i

C ...Ci



D 10 A

however many intervals are chosen, since the waveform is

rectangular.

(iv) Form factor D

rms value

average value

D 1

(v) Peak factor D

maximum value

rms value

D 1

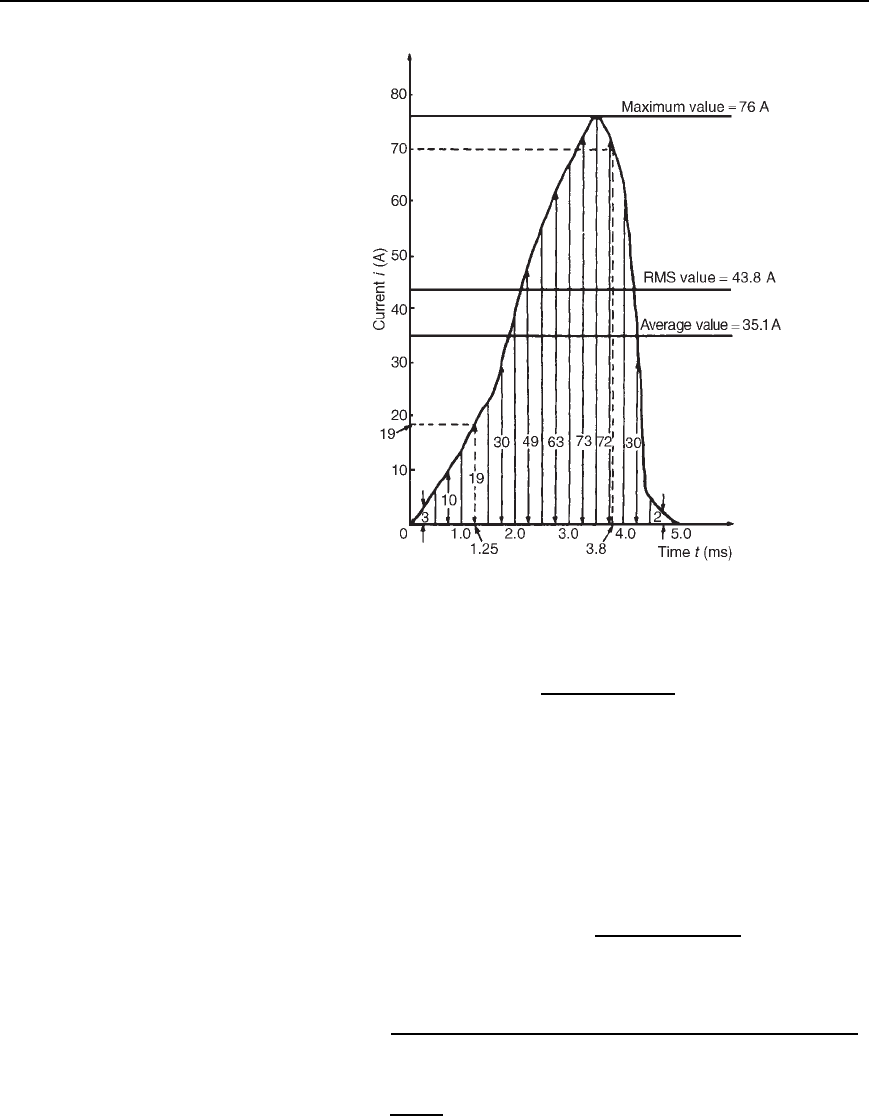
Problem 5. The following table gives the corresponding values of

current and time for a half cycle of alternating current.

time t (ms) 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0

current i (A) 0 7 14 23 40 56 68 76 60 5 0

Assuming the negative half cycle is identical in shape to the positive

half cycle, plot the waveform and ﬁnd (a) the frequency of the

supply, (b) the instantaneous values of current after 1.25 ms and

3.8 ms, (c) the peak or maximum value, (d) the mean or average

value, and (e) the rms value of the waveform.

The half cycle of alternating current is shown plotted in Figure 14.6

(a) Time for a half cycle D 5 ms. Hence the time for 1 cycle, i.e. the

periodic time, T D 10 ms or 0.01 s

Frequency, f D

0.01

D 100 Hz

(b) Instantaneous value of current after 1.25 ms is 19 A, from

Figure 14.6

Instantaneous value of current after 3.8 ms is 70 A, from Figure 14.6

Alternating voltages and currents 199

Figure 14.6

(d) Mean or average value D

area under curve

length of base

Using the mid-ordinate rule with 10 intervals, each of width 0.5 ms

gives:

area under curve D 0.5 ð 10

3

[3 C 10 C 19 C 30 C 49 C 63

C 73 C72 C 30 C 2] (see Figure 14.6)

D 0.5 ð 10

3

351

Hence mean or average value D

0.5 ð 10

3

351

5 ð 10

3

D 35.1 A

(e) rms value





C 10

C 19

C 30

C 49

C 63

C 73

C 72

C 30

C 2







19157



D 43.8A

200 Electrical Circuit Theory and Technology

Problem 6. Calculate the rms value of a sinusoidal current of

maximum value 20 A

For a sine wave, rms value D 0.707 ð maximum value

D 0.707 ð 20 D 14.14 A

Problem 7. Determine the peak and mean values for a 240 V

mains supply.

For a sine wave, rms value of voltage V D 0.707 ð V

A 240 V mains supply means that 240 V is the rms value, hence

0.707

240

0.707

D 339.5V

= peak value

Mean value V

D 0.637V

D 0.637 ð 339.5 D 216.3V

Problem 8. A supply voltage has a mean value of 150 V. Deter-

mine its maximum value and its rms value

For a sine wave, mean value D 0.637 ð maximum value

Hence maximum value D

mean value

0.637

150

0.637

D 235.5 V

rms value D 0.707 ð maximum value D 0.707 ð 235.5 D 166.5 V

Further problems on a.c. values of waveforms may be found in

Section 14.8, problems 4 to 10, page 209.

14.5 The equation of a

sinusoidal waveform

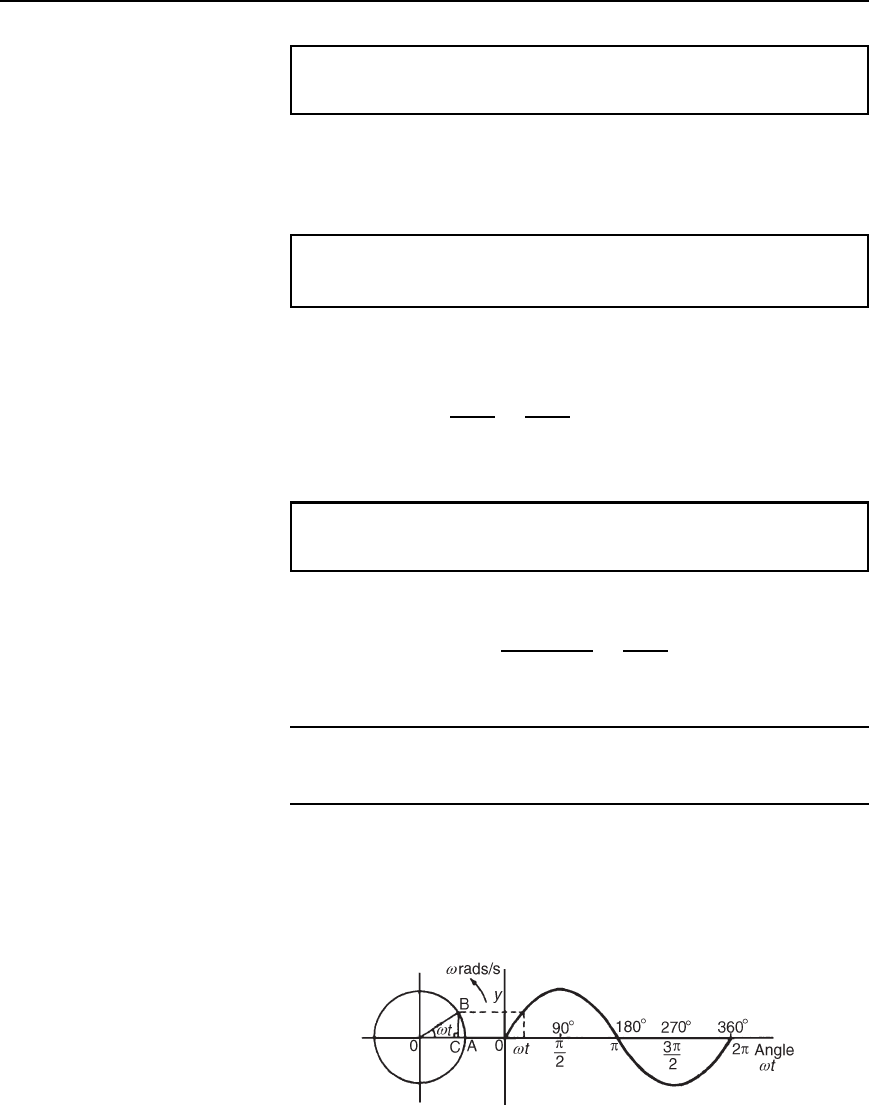
In Fig 14.7, OA represents a vector that is free to rotate anticlockwise

about 0 at an angular velocity of ω rad/s. A rotating vector is known as

a phasor.

Figure 14.7

Alternating voltages and currents 201

Figure 14.8

After time t seconds the vector OA has turned through an angle ωt.If

the line BC is constructed perpendicular to OA as shown, then

sinωt D

i.e. BC D OB sinωt

If all such vertical components are projected on to a graph of y against

angle ωt (in radians), a sine curve results of maximum value OA. Any

quantity which varies sinusoidally can thus be represented as a phasor.

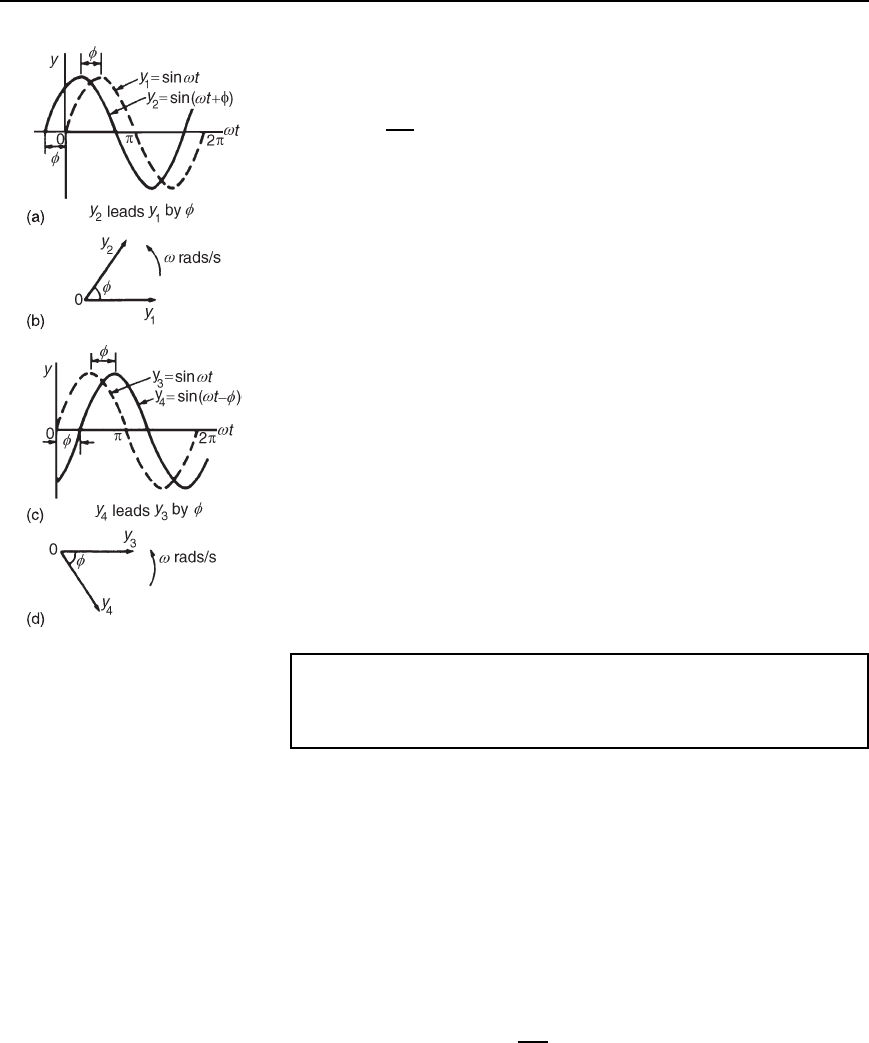
A sine curve may not always start at 0

. To show this a periodic func-

tion is represented by y D sinωt š , where  is the phase (or angle)

difference compared with y D sin ωt. In Figure 14.8(a), y

D sinωt C 

starts  radians earlier than y

D sinωt and is thus said to lead y

 radians. Phasors y

and y

are shown in Figure 14.8(b) at the time

when t D 0.

In Figure 14.8(c), y

D sinωt   starts  radians later than y

sinωt and is thus said to lag y

by  radians. Phasors y

and y

are

shown in Figure 14.8(d) at the time when t D 0.

Given the general sinusoidal voltage,

v = V

sin.!t ± f/, then

(i) Amplitude or maximum value D V

(ii) Peak to peak value D 2V

(iii) Angular velocity D ω rad/s

(iv) Periodic time, T D 2/ω seconds

(v) Frequency, f D ω/2 Hz (since ω D 2 f)

(vi)  D angle of lag or lead (compared with

v D V

sinωt)

Problem 9. An alternating voltage is given by v D 282.8 sin 314t

volts. Find (a) the rms voltage, (b) the frequency and (c) the

instantaneous value of voltage when t D 4ms

(a) The general expression for an alternating voltage is

v D V

sinωt š .

Comparing

v D 282.8sin 314t with this general expression gives the

peak voltage as 282.8 V

Hence the rms voltage D 0.707 ð maximum value

D 0.707 ð 282.8 D 200 V

(b) Angular velocity, ω D 314 rad/s, i.e. 2f D 314

Hence frequency, f D

314

2

D 50 Hz

v D 282.8sin314 ð 4 ð 10

3



D 282.8sin1.256 D 268.9 V

202 Electrical Circuit Theory and Technology

(Note that 1.256 radians D



1.256 ð

180





D 71.96

D 71

Hence v D 282.8sin71

D 268.9 V)

Problem 10. An alternating voltage is given by

v D 75sin200t 0.25 volts.

Find (a) the amplitude, (b) the peak-to-peak value, (c) the rms

value, (d) the periodic time, (e) the frequency, and (f) the phase

angle (in degrees and minutes) relative to 75 sin 200t

Comparing v D 75 sin200t  0.25 with the general expression

v D V

sinωt š  gives:

(a) Amplitude, or peak value D 75 V

(b) Peak-to-peak value D 2 ð 75 D 150 V

(d) Angular velocity, ω D 200 rad/s

Hence periodic time, T D

2

200

100

D 0.01sor10ms

(e) Frequency, f D

0.01

D 100 Hz

(f) Phase angle,  D 0.25 radians lagging 75 sin 200t

0.25 rads D



0.25 ð

180





D 14.32

D 14

Hence phase angle D 14



lagging

Problem 11. An alternating voltage, v, has a periodic time of

0.01 s and a peak value of 40 V. When time t is zero,

v D20 V.

Express the instantaneous voltage in the form

v D V

sinωt š 

Amplitude, V

D 40 V

Periodic time T D

2

hence angular velocity,

ω D

2

0.01

D 200 rad/s

v D V

sinωt C  thus becomes v D 40sin200t C  V

When time t D 0,

v D20 V

Alternating voltages and currents 203

i.e. 20 D 40sin

so that sin  D

20

D0.5

Hence  D arcsin0.5 D30



30 ð



180



rads D



rads

Thus

v= 40sin



200pt −



Problem 12. The current in an a.c. circuit at any time t seconds

is given by: i D 120sin100t C0.36 amperes. Find:

(a) the peak value, the periodic time, the frequency and phase

angle relative to 120sin100t

(b) the value of the current when t D 0

(d) the time when the current ﬁrst reaches 60 A, and

(e) the time when the current is ﬁrst a maximum

(a) Peak value D 120 A

Periodic time T D

2

100

(since ω D 100

D 0.02sor20ms

Frequency, f D

0.02

D 50 Hz

Phase angle D 0.36 rads D



0.36 ð

180





D 20



leading

(b) When t D 0, i D 120sin0 C 0.36 D 120sin20

D 49.3 A



100





C 0.36



D 120sin2.8733D 120 sin 164

 D 31.8A

(d) When i D 60 A, 60 D 120sin100t C0.36

thus

120

D sin100t C0.36

so that 100t C 0.36 D arcsin0.5 D 30



rads D 0.5236 rads

Hence time, t D

0.5236  0.36

100

D 0.521 ms

204 Electrical Circuit Theory and Technology

(e) When the current is a maximum, i D 120 A

Thus 120 D 120sin100t C 0.36

1 D sin100t C0.36

100t C0.36 D arcsin1 D 90



rads D 1.5708 rads

Hence time, t D

1.5708  0.36

100

D 3.85 ms

Further problems on v D V

sinωt š  may be found in Section 14.8,

problems 11 to 15, page 210.

14.6 Combination of

waveforms

The resultant of the addition (or subtraction) of two sinusoidal quantities

may be determined either:

(a) by plotting the periodic functions graphically (see worked Prob-

lems 13 and 16), or

(b) by resolution of phasors by drawing or calculation (see worked Prob-

lems 14 and 15).

Problem 13. The instantaneous values of two alternating currents

are given by i

D 20sinωt amperes and i

D 10sinωt C /3

amperes. By plotting i

and i

on the same axes, using the same

scale, over one cycle, and adding ordinates at intervals, obtain a

sinusoidal expression for i

C i

D 20sinωt and i

D 10sin



ωt C





are shown plotted in Figure 14.9

Ordinates of i

and i

are added at, say, 15

intervals (a pair of dividers

are useful for this).

For example,

at 30

, i

C i

D 10 C 10 D 20 A

at 60

, i

C i

D 8.7 C 17.3 D 26 A

at 150

, i

C i

D 10 C 5 D 5 A, and so on.

The resultant waveform for i

C i

is shown by the broken line in

Figure 14.9. It has the same period, and hence frequency, as i

and i

The amplitude or peak value is 26.5 A.

The resultant waveform leads the curve i

D 20sinωt by 19

i.e.



19 ð



180



rads D 0.332 rads

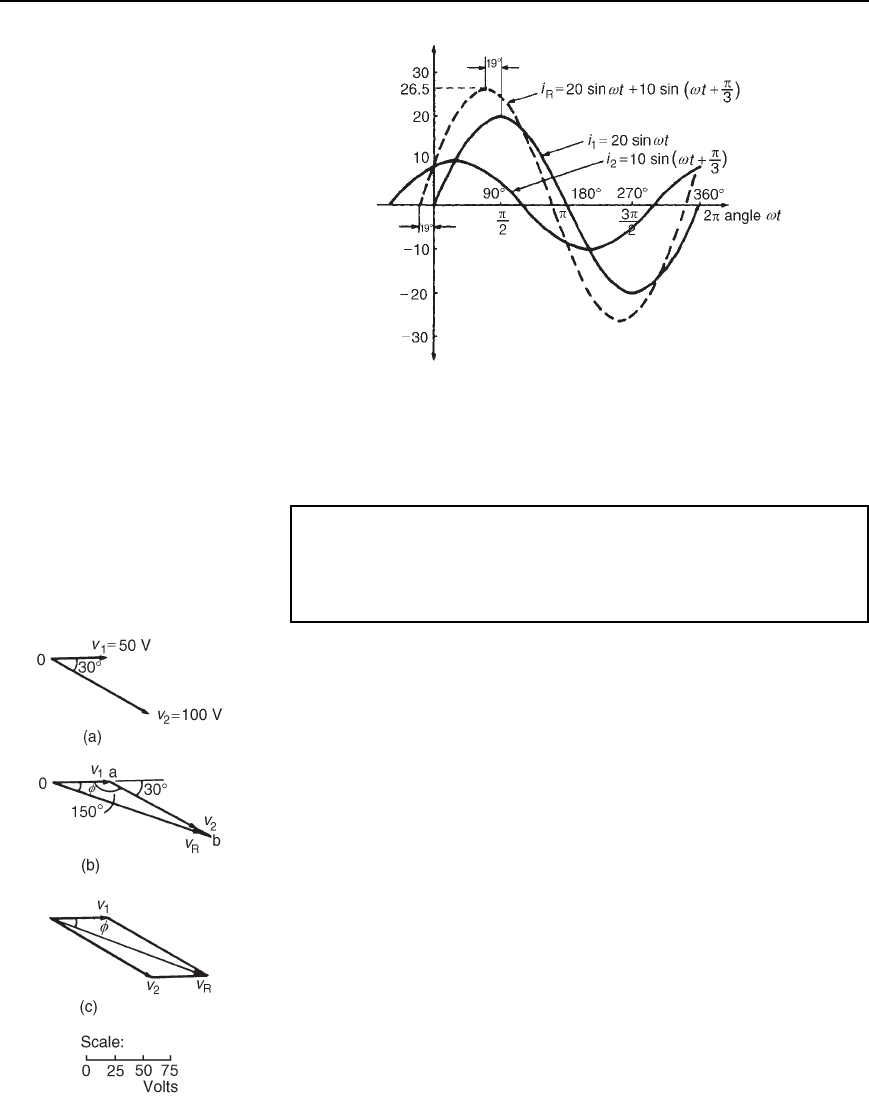
Alternating voltages and currents 205

Figure 14.9

Hence the sinusoidal expression for the resultant i

C i

is given by:

= i

Y i

= 26.5sin.!t Y 0.332/ A

Problem 14. Two alternating voltages are represented by v

50sinωt volts and

D 100sinωt  /6 V. Draw the phasor

diagram and ﬁnd, by calculation, a sinusoidal expression to

represent

C v

Phasors are usually drawn at the instant when time t D 0. Thus v

drawn horizontally 50 units long and

is drawn 100 units long lagging

by /6 rads, i.e. 30

. This is shown in Figure 14.10(a) where 0 is the

point of rotation of the phasors.

Procedure to draw phasor diagram to represent

C v

(i) Draw

horizontal 50 units long, i.e. oa of Figure 14.10(b)

(ii) Join

to the end of v

at the appropriate angle, i.e. ab of

Figure 14.10(b)

(iii) The resultant

D v

C v

is given by the length ob and its phase

angle may be measured with respect to

Alternatively, when two phasors are being added the resultant is always

the diagonal of the parallelogram, as shown in Figure 14.10(c).

From the drawing, by measurement,

D 145 V and angle  D 20

lagging v

A more accurate solution is obtained by calculation, using the cosine

and sine rules. Using the cosine rule on triangle oab of Figure 14.10(b)

gives:

D v

C v

 2v

cos150

D 50

C 100

 250100 cos 150

Figure 14.10