Bichop R.H. (Ed.) Mechatronic Systems, Sensors, and Actuators: Fundamentals and Modeling

Подождите немного. Документ загружается.

19-8 Mechatronic Systems, Sensors, and Actuators

on the thermostat, the output remains off. Once room temperature has increased to the setpoint plus

half the deadband, then the cooling system output goes to fully on. As the room cools, the output stays

fully on until the temperature reaches the setpoint minus half the deadband. At this point the cooling

system output goes fully off.

19.14 System Response

Sensors and actuators respond to inputs that change with time. Any system that changes with time is

considered a dynamic system. Understanding the response of dynamic systems to different types of inputs

is important in mechatronic system design. The most important concept in system response is stability.

The term stability has many different definitions and uses, but the most common definition is related

to equilibrium. A system in equilibrium will remain in the same state in the absence of external distur-

bances. A stable system will return to an equilibrium state if a “small” disturbance moves the system

away from the initial state. An unstable system will not return to an equilibrium position, and frequently

will move “far” from the initial state.

Figure 19.12 illustrates three stability conditions with a simple ball and hill system. In each case an

equilibrium position is easily identified—either the top of the hill or the bottom of the valley. In the

unstable case, a small motion of the ball away from the equilibrium position will cause the ball to move

“far” away, as it rolls down the hill. In the stable case, a small movement of the ball away from the equi-

librium position will eventually result in the ball returning, perhaps after a few oscillations. In the third

case, the absence of friction causes the ball to oscillate continuously about the equilibrium position once

a small movement has occurred. This special case is often known as marginal stability, since the system

never quite returns to the equilibrium position.

Most sensors and actuators are inherently stable. However, the addition of active control systems can

cause a system of stable devices to exhibit overall unstable behavior. Careful analysis and testing is required

to ensure that a mechatronic system acts in a stable manner. The complex response of stable dynamic

systems is frequently approximated by much simpler systems. Understanding both first-order and second-

order system responses to either instantaneous (or step) changes in inputs or sinusoidal inputs will suffice

for most situations.

19.15 First-Order System Response

First-order systems contain two primary elements: an energy storing element and an element which

dissipates (or removes) energy. Typical first-order systems include resistor–capacitor filters and resistor–

inductor networks (e.g., a coil of a stepper motor). Thermocouples and thermistors also form first-order

systems, due to thermal capacitance and resistance. The differential equation describing the time response

of a generic first-order system is

FIGURE 19.12 System stability.

Smooth, no frictionRough, with friction

Marginally stableStableUnstable

dy t()

------------

yt()+ ft()=

9258_C019.fm Page 8 Tuesday, October 2, 2007 1:24 AM

Sensor and Actuator Characteristics 19-9

where y(t) is the dependent output variable (velocity, acceleration, temperature, voltage, etc.), t is the

independent input variable (time),

is the time constant (units of seconds), and f(t) is the forcing

function (or system input).

The solution to this equation for a step or constant input is given by

where y

∞

is the limiting or final (steady-state) value, y

is the initial value of the independent variable at

t = 0.

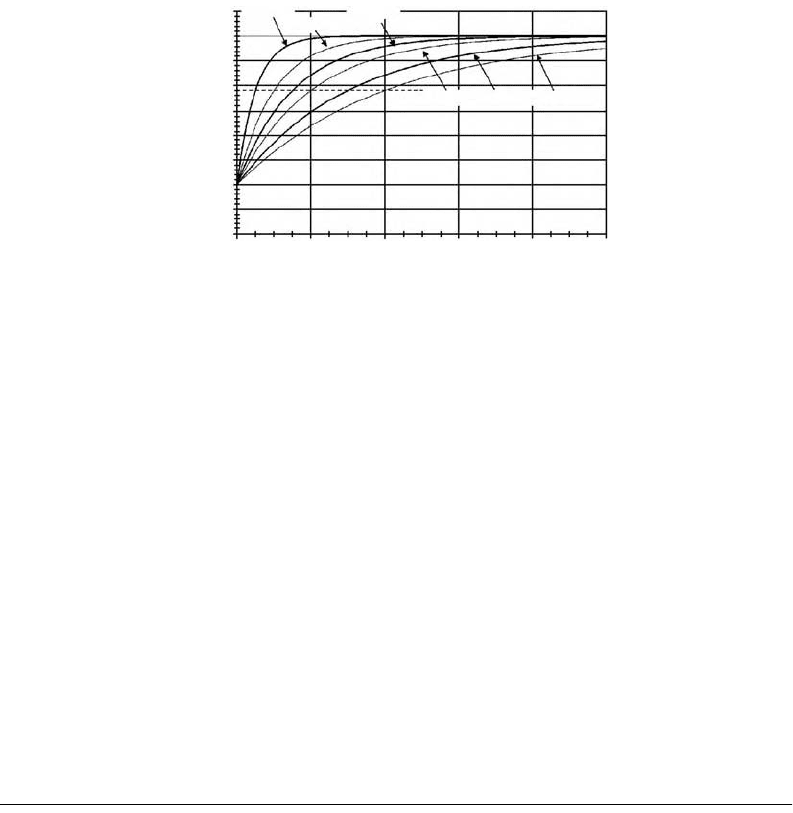
A set of typical first-order system step responses is shown in Figure 19.13. The initial value is arbitrarily

selected as 20 with final values of 80. Time constants ranging from 0.25 to 2 s are shown. Each of these

curves directly indicates its time constant at a key point on the curve. Substituting t =

into the first-

order response equation with y

= 20 and y

∞

= 80 gives

Each curve crosses the y(

) ≈ 57.9 line when its time constant

equals the time t. This concept is

frequently used to experimentally determine time constants for first-order systems.

19.16 Underdamped Second-Order System Response

Second-order systems contain three primary elements: two energy storing elements and an element which

dissipates (or removes) energy. The two energy storing elements must store different types of energy. A

typical mechanical second-order system is the spring–mass–damper combination shown in Figure 19.14.

The spring stores potential energy (PE = kx

), while the mass stores kinetic energy (KE = mv

), where k

is the spring stiffness (typical units of N/m), x is the spring deflection (typical units of m), m is the mass

(typical units of kg), and v is the absolute velocity of the mass (typical units of m/s).

A common electrical second-order system is the resistor–inductor–capacitor (RLC) network, where

the capacitor and inductor store electrical energy in two different forms. The generic form of the dynamic

equation for an underdamped second-order system is

where y(t) is the dependent variable (velocity, acceleration, temperature, voltage, etc.), t is the independent

variable (time), is the damping ratio (a dimensionless quantity),

is the natural frequency (typical

units of rad/s), and f(t) is the forcing function (or input).

FIGURE 19.13 First-order system—step response.

Output, y

Time, t (sec)

2345

= 0.25 s

= 0.75 s

= 2 s

= 0.5 s

= 1 s

= 1.5 s

yt() y

∞

–()e

–

() 80 20 80–()e

1–

+ 57.9==

yt()

--------------

ζω

dy t()

------------

yt()++ft()=

9258_C019.fm Page 9 Tuesday, October 2, 2007 1:24 AM

19-10 Mechatronic Systems, Sensors, and Actuators

The response of an underdamped second-order system to a unit step input can be deter-

mined as:

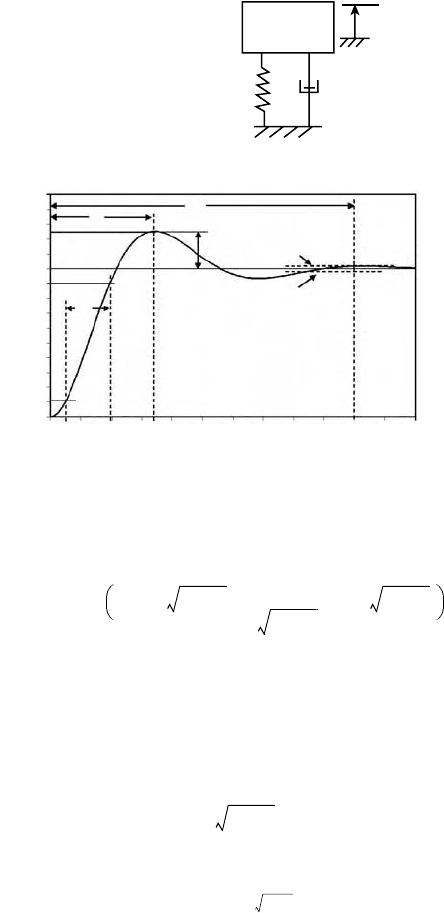
This second-order system step response is often characterized by a set of time response parameters

illustrated in Figure 19.15.

These time response parameters are functions of the damping ratio

and the natural frequency

•

Peak time, T

: the time required to reach the first (or maximum) peak

•

Percent overshoot, %OS: amount the response exceeds or overshoots the steady-state value

•

Settling time, T

: the time when the system response remains within ±2% of the steady-state value

•

Rise time, T

: time required for the response to go from 10% to 90% of the steady-state value.

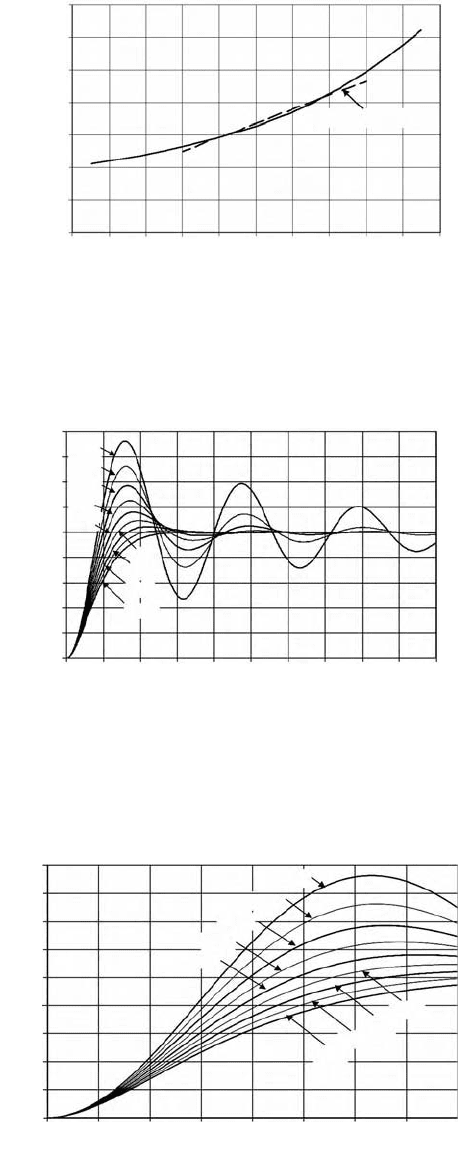
Figure 19.16 shows the nondimensional rise time (

) as a function of damping ratio, z. A

frequently used approximation relating these two parameters is

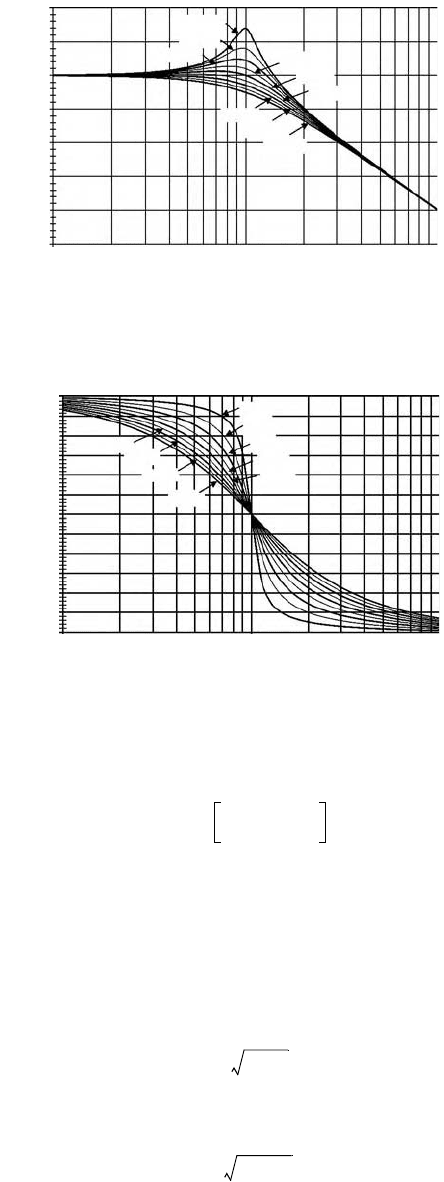
Figures 19.17 and 19.18 show the unit step response of a second-order system as a function of damping

ratio

FIGURE 19.14 Spring–mass–damper system.

FIGURE 19.15 Second-order system—step response.

Output, y

0.3

1.1

1.2

1.3

1.4

1.5

0.5

0.6

0.7

0.8

0.9

0.4

0.1

0.2

213

y = 0.98

Overshoot (OS)

y = 1.02

4 5 6 7 8 9 10 11 12

Nondimensional time,

1<≤()

yt() 1 e

ζω

t–

– t

–

------------------

– tsin+cos–=

–

-------------------------

%OS 100= e

ζπ

–()–

ζω

---------

2.16

0.6 0.3

0.8≤+≈

9258_C019.fm Page 10 Tuesday, October 2, 2007 1:24 AM

Sensor and Actuator Characteristics 19-11

FIGURE 19.16 Rise time versus damping ratio,

FIGURE 19.17 Second-order system step response versus damping ratio,

FIGURE 19.18 Initial second-order system step response versus damping ratio,

0.5

1.5

2.5

3.5

0.1 0.4 0.5 0.6 0.7 0.8 0.9 10.30.2

= 2.16 + 0.6

Damping ratio,

Nondimensional rise time,

Nondimensional time,

Output, y

1.8

1.6

1.4

1.2

1.1

0.8

0.6

0.4

0.2

0246810121416

= 0.1

= 0.2

= 0.3

= 0.4

= 0.5

= 0.6

= 0.7

= 0.8

= 0.9

18 20

Nondimensional time,

Output, y

1.8

0.8

0.6

0.4

0.2

1.6

1.4

1.2

= 0.1

= 0.2

= 0.3

= 0.4

= 0.5

= 0.6

= 0.7

= 0.8

= 0.9

0 0.5 1 1.5 2 2.5 3 3.5 4

9258_C019.fm Page 11 Tuesday, October 2, 2007 1:24 AM

19-12 Mechatronic Systems, Sensors, and Actuators

19.17 Frequency Response

The response of any dynamic system to a sinusoidal input is called the frequency response. A generic

first-order system with a sinusoidal input of amplitude A would have the dynamic equation of

where

is the frequency of the sinusoidal input and

is the first-order time constant. The steady-state

solution to this equation is

where is the amplitude ratio (a dimensionless quantity), and Φ = −tan

−1

(

τω

) is the

phase angle.

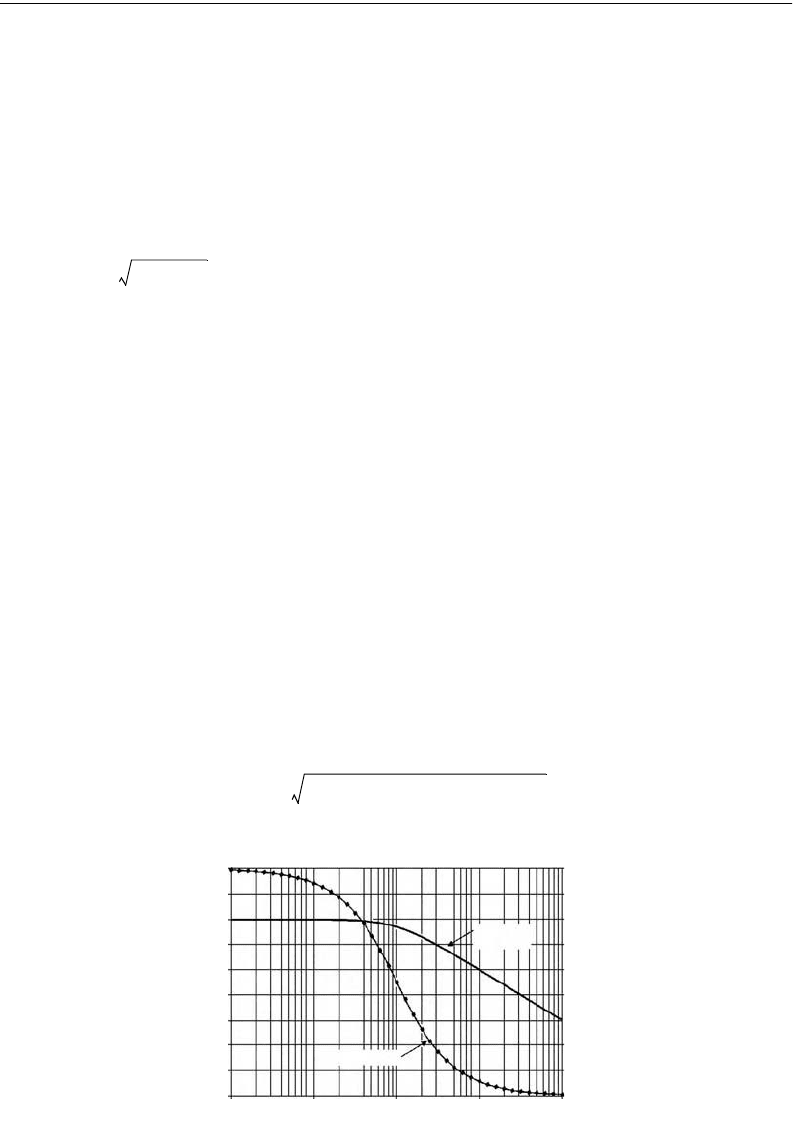
Figure 19.19 is a plot of the magnitude ratio M

and the phase angle Φ as a function of the non-

dimensional frequency,

τω

. Note that the magnitude is frequently plotted in terms of decibels, where M

= 20 log

(M).

The frequency at which the magnitude ratio equals 0.707 (or –3 dB) is called the bandwidth. For a

first-order system, the bandwidth is inversely proportional to the time constant. So,

= 1/

A generic second-order system with a sinusoidal input of amplitude A and frequency

would have

the dynamic equation of

The steady-state solution to this equation is

where

FIGURE 19.19 Frequency response for first-order system.

dy t()

------------

yt()+ ft() A

t()sin==

yt() AM

t Φ+()sin=

M 1/ τω()

1+=

yt()

--------------

ζω

dy t()

------------

yt()++A

t()sin=

yt()

---------

t Φ+()sin

()–[]

ζω

()[]

-----------------------------------------------------------------------------

Nondimensional frequency,

τω

Phase angle

Magnitude

ratio

Magnitude ratio, M

Phase angel, f (degree)

0.01

–10

–20

–30

–40

–50

–60

–70

–20

–10

–30

–40

–50

–60

–70

–80

–90

0.1 1 10 100

9258_C019.fm Page 12 Tuesday, October 2, 2007 1:24 AM

Sensor and Actuator Characteristics 19-13

is the amplitude ratio (a dimensionless quantity), and

is the phase angle.

Figures 19.20 and 19.21 are plots of the magnitude response M

= 20 log

(M) and the phase angle

Φ for the second-order system as a function of damping ratio,

. The peak value in the magnitude

response, M

, can be found by taking the derivative of M with respect to

and setting the result to zero

to find (Nise, 1995)

This peak value in M occurs at the frequency

given by

FIGURE 19.20 Frequency response magnitude for second-order system.

FIGURE 19.21 Frequency response phase angle for second-order system

Nondimensional frequency,

Magnitude ratio, M

0.1 1 10

–10

–20

–30

–40

–50

= 0.1

= 0.2

= 0.3

= 0.4

= 0.5

= 0.6

= 0.7

= 0.8

= 0.9

Nondimensional frequency,

–10

–40

–70

–100

–120

–130

–150

–160

–180

0.1

Phase angle, Φ (degrees)

101

= 0.1

= 0.2

= 0.3

= 0.4

= 0.5

= 0.6

= 0.7

= 0.8

= 0.9

Φ tan

−1

ζω

()

()–

----------------------------

–=

–

------------------------

–=

9258_C019.fm Page 13 Tuesday, October 2, 2007 1:24 AM

19-14 Mechatronic Systems, Sensors, and Actuators

The peak value in an experimentally determined frequency response can be used to estimate both the

natural frequency and damping ratio for a second-order system. These parameters can then be used to

estimate time domain responses such as peak time and percent overshoot.

Reference

Nise, N. S., Control Systems Engineering, 2nd ed., Benjamin/Cummings, 1995.

9258_C019.fm Page 14 Tuesday, October 2, 2007 1:24 AM

20-1

Sensors

20.1 Linear and Rotational Sensors .............................. 20-2

Contact

•

Infrared

•

Resistive

•

Tilt (Gravity)

•

Capacitive

•

AC Inductive

•

DC Magnetic

•

Ultrasonic

•

Magnetos-

trictive Time-of-Flight

•

Laser Interferometry

•

References

20.2 Acceleration Sensors .............................................. 20-12

Overview of Accelerometer Types

•

Dynamics and

Characteristics of Accelerometers

•

Vibrations

•

Typ ic al

Error Sources and Error Modeling

•

Inertial

Accelerometers

•

Electromechanical Accelerometers

•

Piezoelectric Accelerometers

•

Piezoresistive

Accelerometers

•

Strain-Gauge Accelerometers

•

Electrostatic

Accelerometers

•

Micro- and Nanoaccelerometers

•

Signal

Conditioning and Biasing

•

References

20.3 Force Measurement ................................................ 20-34

General Considerations

•

Hooke’s Law

•

Force Sensors

20.4 Torque and Power Measurement .......................... 20-48

Fundamental Concepts

•

Arrangements of Apparatus for

Torque and Power Measurement

•

Torq u e Tr an sd u cer

Te c h n o l o g i e s

•

Torque Transducer Construction,

Operation, and Application

•

Apparatus for Power

Measurement

•

References

20.5 Flow Measurement ................................................. 20-62

Introduction

•

Te r m i n o l o g y

•

Flow Characteristics

•

Flowmeter Classification

•

Differential Pressure

Flowmeter

•

Variable Area Flowme ter

•

Positive

Displacement Flowmeter

•

Turbine Flowme ter

•

Vortex Shedding Flowmeter

•

Electromagnetic

Flowmeter

•

Ultrasonic Flowmeter

•

Coriolis

Flowmeter

•

Two-Phase Flow

•

Flowmeter

Installation

•

Flowmeter Selection

•

References

20.6 Temperature Measurements .................................. 20-73

Introduction

•

Thermometers That Rely Upon Differential

Expansion Coefficients

•

Thermometers That Rely Upon

Phase Changes

•

Electrical Temperature Sensors and

Tr a n s d u c e r s

•

Noncontact Thermometers

•

Microscale

Temperature Measurements

•

Closing

Comments

•

References

20.7 Distance Measuring and Proximity Sensors ........ 20-88

Distance Measuring Sensors

•

Proximity Sensors

20.8 Light Detection, Image, and Vision Systems ....... 20-119

Introduction

•

Basic Radiometry

•

Light Sources

•

Light

Detectors

•

Image Formation

•

Image Sensors

•

Vision

Systems

•

References

20.9 Integrated Microsensors ........................................ 20-136

Introduction

•

Examples of Micro- and Nanosensors

•

Future Development Trends

•

Conclusions

•

References

20.10 Vision ...................................................................... 20-153

Digital Images

•

System Setup and Calibration

•

Machine

Vision

•

References

Kevin M. Lynch

Northwestern University

Michael A. Peshkin

Northwestern University

Halit Eren

Curtin University of Technology

M. A. Elbestawi

McMaster University

Ivan J. Garshelis

Magnova, Inc.

Richard Thorn

University of Derby

Pamela M. Norris

University of Virginia

Bouvard Hosticka

University of Virginia

Jorge Fernando Figueroa

NASA Stennis Space Center

H. R. (Bart) Everett

Space and Naval Warfare Systems

Center

Stanley S. Ipson

University of Bradford

Chang Liu

University of Illinois

Nicolas Vazquez

Dinesh Nair

University of Texas

9258_C020.fm Page 1 Tuesday, October 9, 2007 9:08 PM

20-2 Mechatronic Systems, Sensors, and Actuators

20.1 Linear and Rotational Sensors

Kevin M. Lynch and Michael A. Peshkin

By far the most common motions in mechanical systems are linear translation along a fixed axis and

angular rotation about a fixed axis. More complex motions are usually accomplished by composing these

simpler motions. In this chapter we provide a summary of some of the many technologies available for

sensing linear and rotational motion along a single axis. We have arranged the sensing modalities

according to the physical effect exploited to provide the measurement.

20.1.1 Contact

The simplest kind of displacement sensor is a mechanical switch which returns one bit of information:

touching or not touching. A typical microswitch consists of a lever which, when depressed, creates a

mechanical contact within the switch, which closes an electrical connection (Figure 20.1). Microswitches

may be used as bump sensors for mobile robots, often by attaching a compliant material to the lever

(such as a whisker) to protect the robot body from impact with a rigid obstacle. Another popular

application of the microswitch in robotics is as a limit switch, indicating that a joint has reached the limit

of its allowable travel.

Figure 20.2 shows a typical configuration for a microswitch. The pull-up resistor keeps the signal at

+V until the switch closes, sending the signal to ground. As the switch closes, however, a series of micro-

impacts may lead to “bounce” in the signal. A “debouncing” circuit may be necessary to clean up the

output signal.

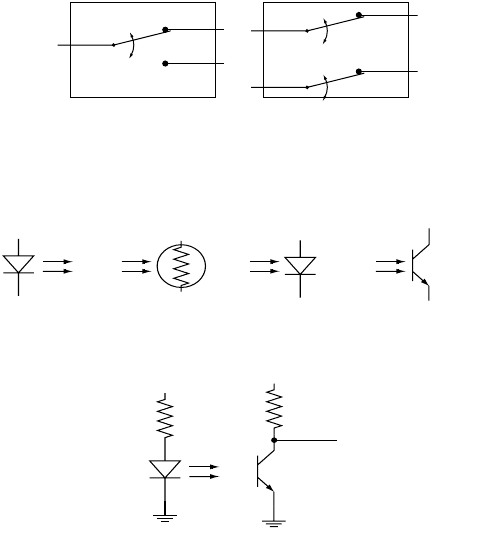
Switches may be designated NO or NC for normally open or normally closed, where “normally”

indicates the unactivated or unpressed state of the switch. A switch may also have multiple poles (P) and

one or two throws (T) for each pole. A pole moves as the switch is activated, and the throws are the

possible contact points for the pole. Thus an SPDT (single pole double throw) switch switches a single

pole from contact with one throw to the other, and a DPST (double pole single throw) switch switches

two poles from open to closed circuit (Figure 20.3).

FIGURE 20.1 A typical microswitch.

FIGURE 20.2 Signal bounce at a closing switch.

9258_C020.fm Page 2 Tuesday, October 9, 2007 9:08 PM

Sensors 20-3

20.1.2 Infrared

Infrared light can be used in a variety of ways to measure linear and rotational displacement. Typically,

an infrared light-emitting diode (LED), or photoemitter, is used as a source, and an infrared sensitive

device is used to detect the emitted light. The detector could be a photoresistor or photocell, a variable

resistor which changes resistance depending on the strength of the incident light (possibly infrared or

visible); a photodiode, which allows the flow of electrical current in one direction in the presence of

infrared light, and otherwise acts as an open circuit; or a phototransistor. In a phototransistor, the incident

infrared light acts as the base current for the transistor, allowing the flow of collector current proportional

to the strength of the received infrared light (up to saturation of the transistor). Circuit symbols for the

various elements are shown in Figure 20.4.

If the emitter and detector are facing each other, they can be used as a beam-breaker, to detect if

something passes between. This is called a photointerrupter (Figure 20.5). If the emitter and detector are

free to move along the line connecting them, the strength of the received signal can be used to measure

the distance separating them. Infrared photodetectors may be sensitive to ambient light, however. To

distinguish the photoemitter light from background light, the source can be modulated (i.e., switched

on and off at a high frequency), and the detector circuitry designed to respond only to the modulated

infrared.

An emitter and detector facing the same direction can be used to roughly measure the distance to a

nearby surface by the strength of the returned light reflecting off the surface. This is called a

photoreflector

(Figure 20.6). Alternatively, such a sensor could be used to detect light absorbing or light reflecting surfaces

at a constant distance, as in mobile robot line following. Light polarizing filters can also be used on the

emitter and detector so that the detector only recognizes light reflected by a special “optically active”

retroreflecting surface.

FIGURE 20.3 SPDT and DPST switch configurations.

FIGURE 20.4 Optoelectronic circuit symbols and a typical emitter/detector configuration.

SPDT

DPST

LED Photoresistor Photodiode Phototransistor

signal

Typical configuration

9258_C020.fm Page 3 Tuesday, October 9, 2007 9:08 PM