Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

13 Unconventional Superconductivity in Novel Materials 721

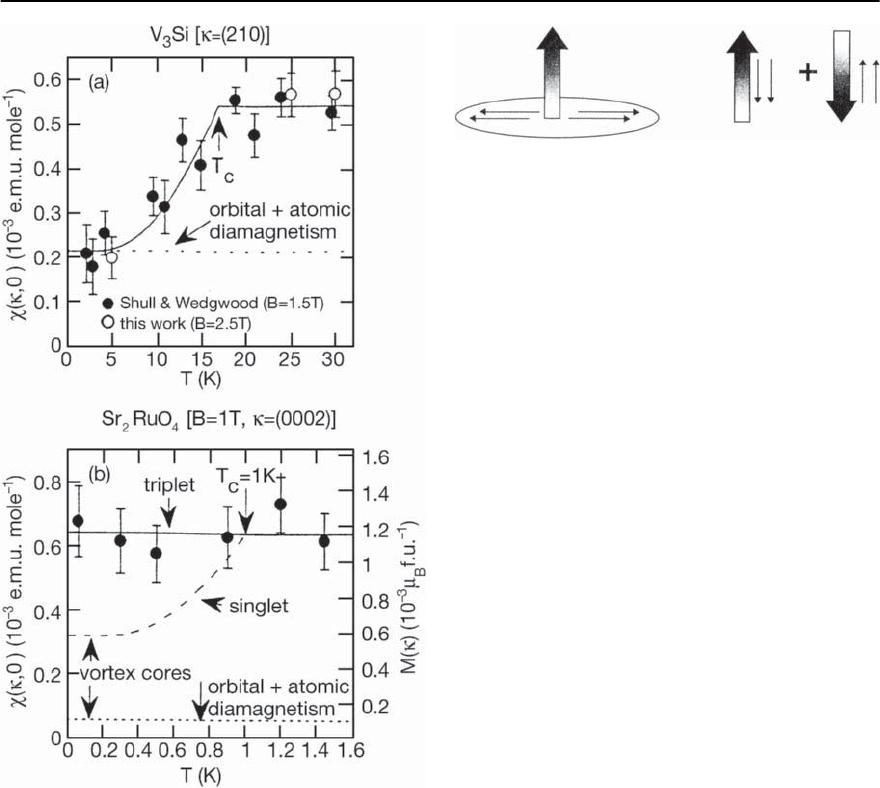
Fig. 13.85. Conduction electron spin susceptibility in the

superconducting state 

for an s-wave superconductor

Si) and Sr

RuO

, based on spin polarized neutron scat-

tering measurements [567]. In (a), the original work of

Shull and Wedgewood [568] is confirmed and the data are

described well by the Yosida function. In (b),thetempera-

ture independence of 

for Sr

RuO

is in marked contrast

to that expected if Sr

RuO

had singlet spin pairing, af-

ter [569]

ing can increase 

(T) for spin-singlet pairing, it is

not expected to be strong enough in Sr

RuO

to in-

crease 

(T)to

(T) [570].The behavior of 

(T) for

the s-wave superconductor V

Si and the unconven-

tional superconductor Sr

RuO

,basedonspinpo-

Fig. 13.86. Spin triplet superconducting states correspond-

ing to d(k)=ˆz(k

+ ik

)(left)andd(k)=ˆxk

+ ˆyk

(right)

The ˆz(k

+ ik

) state has an angular momentum along the

z-axis (thick arrow) and spins perpendicular in the plane

(thin arrows)Theˆxk

+ ˆyk

state has vanishing total an-

gular momentum because the orbital angular momentum

is compensated by the spins of the Cooper pair. Experi-

ments indicate that the superconducting phase in Sr

RuO

isofthetypeshownintheleft panel; i.e.,a state with finite

angular momentum, after [570]

larized neutron scattering measurements of Duffy

et al. [567], are shown in Fig. 13.85. Other evidence

for unconventional superconductivity in Sr

RuO

the extreme sensitivity of the superconductivity to

nonmagnetic impurities; T

vanishes for Al or Si im-

purity concentrations corresponding to a mean free

path that is comparable to the superconducting co-

herence length. One of the most intriguing results

comes from ‹SR measurements on Sr

RuO

that re-

veal an enhancement in the zero field relaxation rate

in the superconducting state that is consistent with

a superconducting state with broken time reversal

symmetry [322]. A variety of experiments indicate

that the superconducting energy gap has nodes or

very deep minima,although thee form of these nodes

is still uncertain.

The spin-triplet superconducting state that seems

to be favored by experiments on Sr

RuO

has the

form d(k)=ˆz(k

+ ik

). This state and another

spin-triplet state are schematically represented in

Fig. 13.86 [570]. The ˆz(k

+ ik

) state has angular

momentum along the z-axis (thick arrow) and spins

perpendicular in the plane (thin arrows), while the

ˆxk

+ ˆyk

state has vanishing total angular momen-

tum because the orbital angular momentum is com-

pensated by the spins of the Cooper pair [570]. A

comprehensive review of the normal and supercon-

ducting state properties of Sr

RuO

and the physics

of spin-triplet pairing can be found in [569].

Quantum spin ladder materials have attracted

much interest [575,576]. These materials consist of

722 M.B. Maple et al.

Table 13.7.(a) Some important classes of cuprate superconductors and the maximum value of

observed in each class. (b) Examples of the abbreviated names (nicknames) used to denote

cuprate materials

(a)

Material Max. T

(K)

2−x

CuO

; M = Ba, Sr, Ca, Na ∼ 40

2−x

CuO

4−y

;Ln=Pr,Nd,Sm,Eu;M=Ce,Th ∼ 25

YBa

7−ı

LnBa

7−ı

∼ 95

Ce, Tb do not form phase.

Pr forms phase; neither metallic nor superconducting.

RBa

∼ 80

n−1

2n+4

(n = 1,2,3,4) (n = 3) 110

TlBa

n−1

2n+3

(n = 1,2,3,4) (n = 4) 122

n−1

2n+4

(n = 1,2,3,4) (n = 3) 122

HgBa

n−1

2n+2

(n = 1,2,3,4) (n = 3) 133

(b)

Material Nickname

YBa

7−ı

YBCO; YBCO–123; Y–123

BSCCO; BSCCO–2223; Bi–2223

TBCCO; TBCCO–2223; Tl–2223

HgBa

HBCCO; HBCCO–1223; Hg–1223

1.85

0.15

CuO

LSCO

1.85

0.15

CuO

4−y

NCCO

ladders made of AFM chains of S =1/2spinscoupled

by inter-chain AFM bonds. Examples of two-leg lad-

der materials are SrCu

and LaCuO

2.5

;anexample

of a three-leg ladder material is Sr

. Supercon-

ductivity has been discovered in the ladder material

0.4

13.6

41.84

under pressure with T

≈ 12

K at 3 GPa [577]. Interest in quantum spin ladder

materials is partly due to the fact that they are sim-

ple model systems for theories of superconductivity

based on magnetic pairing mechanisms.

Approximately 100 different cuprate materials,

many of which are superconducting, have been dis-

covered since 1986. Several of the more important

high T

cuprate superconductors are listed in Table

13.7, along with the maximum values of T

observed

in eachclass of materials.Included in the table are ex-

amples of abbreviated designations (nicknames) for

specific cupratematerials whichwe will use through-

out this article (e.g., YBa

7−ı

=YBCO,YBCO-

123,Y-123).

It is interesting to note that superconductivity

with values of T

in the neighborhood of 30–40 K

has been found in several noncuprate materials: the

cubic perovskite Ba

1−x

BiO

≈ 30 K) [578,579],

the fcc “buckeyball” compound Rb

≈ 29

K) [580, 581], and the compound MgB

≈ 39

K) [582].

13.5.3 Structure and Charge Carrier Doping

The high T

cuprate superconductors have layered

perovskite-like crystal structures which consist of

conducting CuO

planes separated by layers com-

prised of other elements, denoted as A, and oxygen,

13 Unconventional Superconductivity in Novel Materials 723

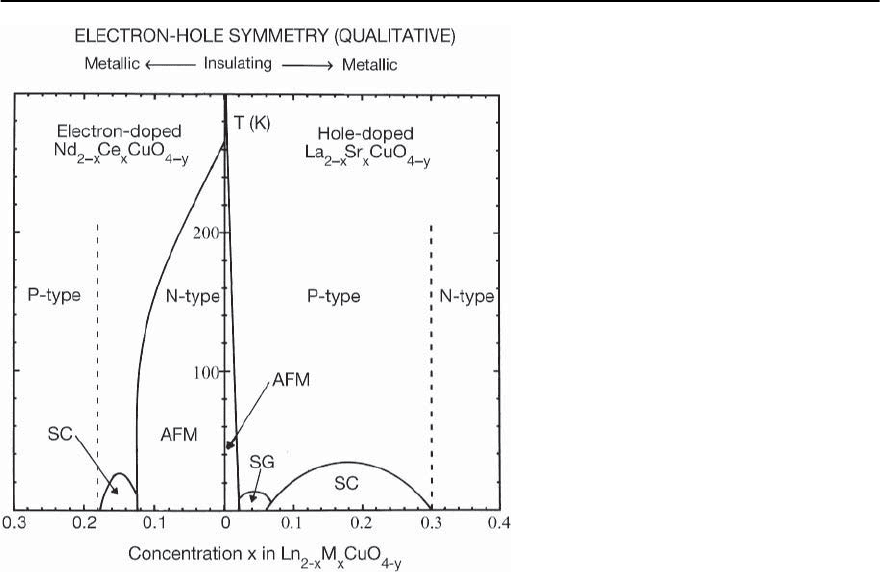
Fig. 13.87. Temperature-dopant concentration

(T–x) phase diagram delineating the re-

gions of superconductivity and antiferromag-

netic ordering of the Cu

ions for the

hole-doped La

2−x

CuO

and electron-doped

2−x

CuO

4−y

systems. AFM = antiferro-

magnetic phase, SG = spin-glass phase, and SC

= superconducting phase, after [585]

,and,in some cases,layers of Ln ions [583,584].

The mobile charge carriers, which can be electrons

but are usually holes,are generally believed to reside

primarily within the CuO

planes. The A

layers

apparently function as charge reservoirs that control

the doping of the CuO

planes with charge carri-

ers and as spacers that govern the anisotropy of the

physical properties of the materials.

Many of the cuprates can be doped with charge

carriers and rendered superconducting by substi-

tuting appropriate elements into an AFM insulat-

ing parent compound. For example, substitution of

divalent Sr for trivalent La in the AFM insulator

CuO

dopes the CuO

planes with mobile holes

and produces superconductivity in La

2−x

CuO

with a maximum T

of ∼ 40 K at x ≈ 0.17 [549].

Similarly, substitution of tetravalent Ce for triva-

lent Nd in the AFM insulating compound Nd

CuO

apparently dopes the CuO

planes with electrons,

resulting in superconductivity in Nd

2−x

CuO

4−y

with a maximum T

of ∼ 25 K at x ≈ 0.15 for y

≈ 0.02 [556,585]. The temperature T vs x phase di-

agrams for the La

2−x

CuO

and Nd

2−x

CuO

4−y

systems are shown in Fig. 13.87 [585].

The Ln

2−x

CuO

4−y

electron-doped materials

have a tetragonal crystal structure that is similar

to that of the La

2−x

CuO

hole-doped materials,

but without the apical oxygen atoms. The crys-

tal structures of the La

CuO

and Nd

CuO

parent

compounds are displayed in Fig. 13.88 [585]. The

2−x

CuO

and Nd

2−x

CuO

4−y

systems have

one CuO

plane per unit cell and are referred to as

single CuO

layer compounds. Other superconduct-

ing cuprate systems have more than one CuO

plane

per unit cell: LnBa

7−ı

has two CuO

planes

per unit cell (double CuO

layer compound), while

n−1

has n CuO

layers per unit cell (n

CuO

layer compound) and can be synthesized by

conventional methods for n =1, 2, or 3.

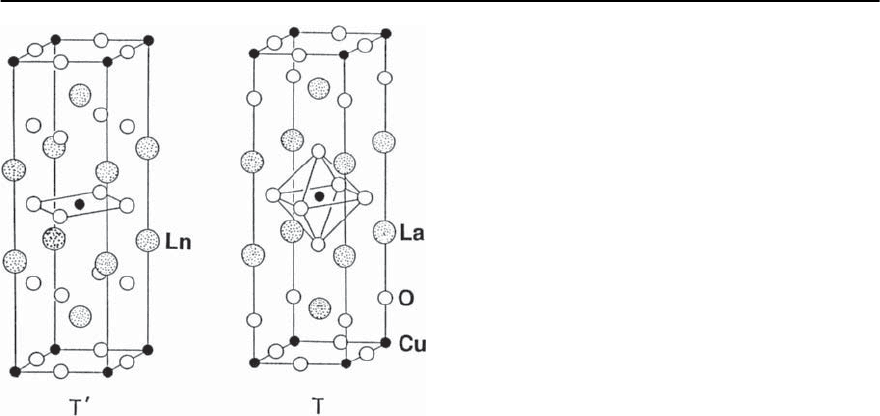
724 M.B. Maple et al.

Fig. 13.88. Crystal structures of La

CuO

(T-phase) and

CuO

(Ln = Pr, Nd, Sm, Eu, Gd; T



-phase) parent com-

pounds, after [585]

13.5.4 Superconducting Properties

Critical Field and Critical Current Density

With values of T

in excess of the boiling tempera-

ture of liquid nitrogen (77 K) for some compounds,

the high T

cuprates were immediately recognized

as promising candidates for technological applica-

tions of superconductivity,since they can be cooled

into the superconducting state using liquid nitrogen,

closed cycle refrigerators, and other more econom-

ical refrigeration techniques. Cuprates such as the

RBa

7−ı

compounds (T

in the range 92 − 95 K)

have enormous critical fields ∼ 10

tesla [554,586]

thataremorethanadequateformosthigh-current

and high-field technological applications. Shown in

Fig. 13.89 is the resistively determined upper critical

field H

(T) curve for the compound YbBa

7−ı

Extrapolation of the H

(T) curves measured be-

tween 0 and ∼ 10 T to T =0K,usingthetheory

developed by Werthamer, Helfand, and Hohenberg

(WHH) in 1966 without paramagnetic limiting [18],

yields a value of H

(0) ≈ 160 T [554].

Epitaxially grown thin films of YBa

7−ı

single crystal SrTiO

substrates have critical current

densities J

≈ 10

A/cm

in zero field that decrease

relatively slowly with magnetic field, making them

suitable for technological applications [587]. Tech-

niques have been devised that yield values of J

high fields for in-plane grain oriented thin films of

YBa

7−ı

on ﬂexible substrates at 64 K (pumped

liquid nitrogen temperatures) that exceed those of

NbTi and Nb

Sn at liquidhelium temperatures [588].

Presently, two of the leading candidates for tech-

nological applications of superconductivity are the

RBa

7−ı

andBi

n−1

2n+4

(n =2,3)ma-

terials. The first generation superconducting tapes

and wires are based on both substituted and unsub-

stituted Bi

n−1

2n+4

(n = 2,3) superconduc-

torspreparedbythepowder-in-tube technique[589].

Superconducting Pairing Mechanism

Two features in the T − x phase diagrams for

2−x

CuO

and Nd

2−x

CuO

4−y

in Fig. 13.87

would appear to be relevant to cuprate supercon-

ductivity: (i) the electron-hole phase-diagram may

provide a constraint on viable theories of high T

in cuprates, and (ii) the proximity of antiferromag-

netism suggests that superconducting electron pair-

ing in the cuprates may be mediated by AFM spin

ﬂuctuations. An AFM pairing mechanism is con-

sistent with the occurrence of d-wave pairing with

−y

symmetry that is suggested by experiments on

several hole-doped cuprates (discussed later in this

article) article). Several theoretical models (for ex-

ample, [592,593]), based on AFM spin ﬂuctuations,

have predicted d-wave superconductivitywith d

−y

symmetry for the cuprates. In contrast to the ap-

parent electron-hole symmetry in the T − x phase

diagrams of hole and electron-doped cuprates, there

appears to be an interesting electron-hole “antisym-

metry” in the pressure dependence of T

.Thisisil-

lustrated in Fig. 13.90 which contains a plot of the

relative change of T

with applied pressure,dlnT

/dP,

vs T

for the electron-doped superconductors and a

comparison of these data with similar data for vari-

ous hole-doped cuprate superconductors[591].

Other features are consistent with non-phonon-

mediated pairing in the hole-doped cuprates. The

curve of T

vs carrier concentration can be ap-

proximated by an inverted parabola with the max-

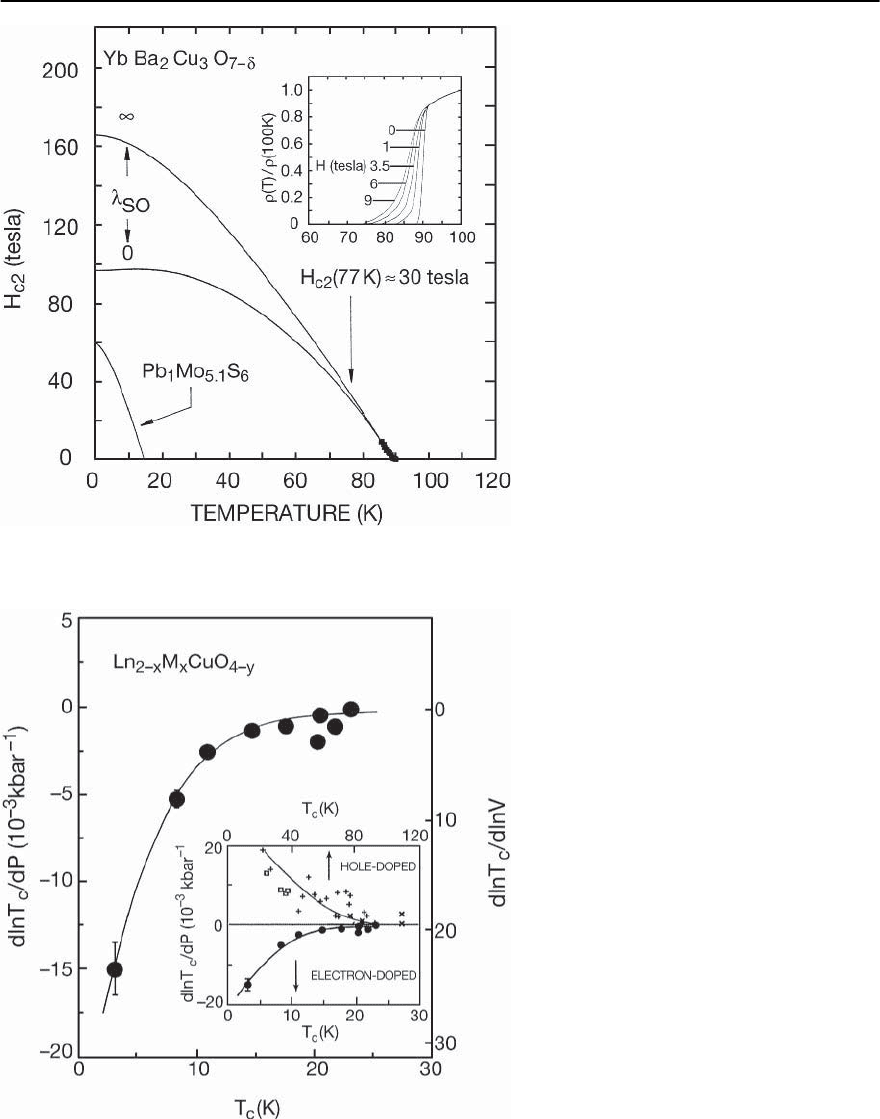
13 Unconventional Superconductivity in Novel Materials 725

Fig. 13.89. Upper critical field H

vs tempera-

turefor the compoundYbBa

7−ı

.Thesolid

lines are based on standard WHH [18] theory

for a conventional type II superconductor in

the limits of maximum (spin-orbit scattering

parameter 

= 0) and minimum (

= ∞)

paramagnetic limitation and have been fitted

to the data near T

.Inset: Normalized electrical

resistivity vs temperature in several magnetic

fields between 0 and 9 tesla, after [557]

Fig. 13.90. Relative rate of change of T

with

applied pressure P,dlnT

/dP,asafunction

of T

for the electron-doped superconductors

2−x

CuO

4−y

(Ln = Pr, Nd, Sm, Eu; M = Ce,

Th; x ≈0.15; y ≈0.03).Inset: Same data plotted

together with similar data for hole-doped su-

perconductors from [590]. (: La-based “214”;

+: R-based“123”; x: Bi–Sr– and Tl–Ba–Ca–Cu–

O materials), after [591]

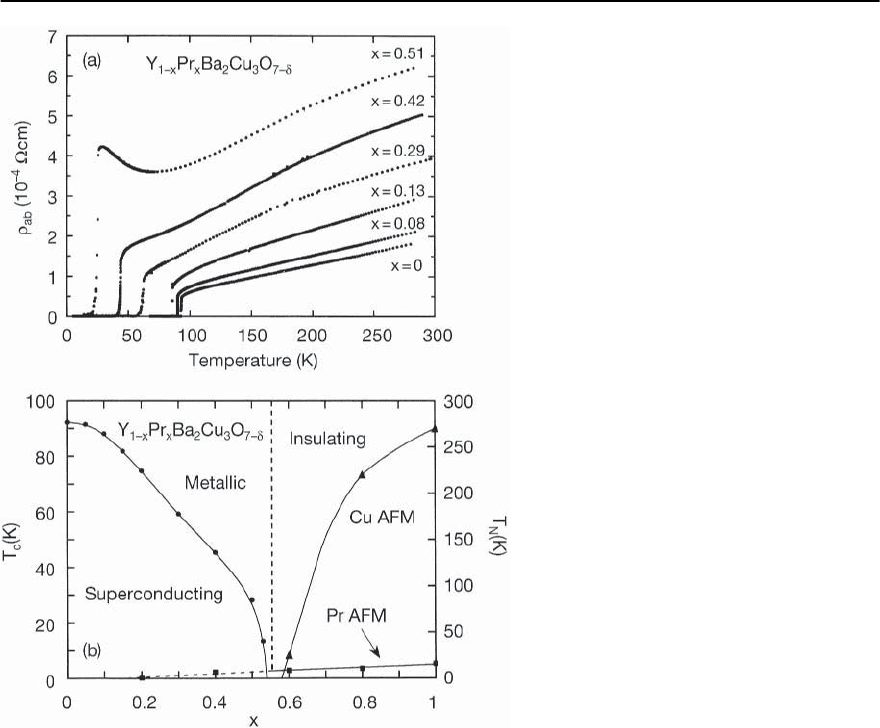
726 M.B. Maple et al.

Fig. 13.91. (a) In-plane electrical resistivity 

vs temperatureT curves forY

1−x

7−ı

(0 < x < 0.51) single crystals, after [282].

(b) Temperat ur e T vs Pr concentration x phase

diagram for the Y

1−x

7−ı

system,de-

lineating metallic, superconducting, insulating,

and antiferromagnetically ordered regions, af-

ter [282,596]

imum value of T

occurring at an optimal dopant

concentration x

[594]. (Note that the terminology

“under-doped” refers to values of x smaller than the

“optimally-doped” value x

where T

is maximized,

whereas“over-doped”refers to values of x larger than

.) The isotope effect on T

for optimally-dopedma-

terial is material is essentially zero (i.e., T

∝ M

−˛

with ˛ ≈ 0; M = ion mass) [595].

An interesting example of the inverted parabolic

dependence of T

on carrier concentration is pro-

vided by theY

1−x−y

7−ı

system. In this

system, the Ca

and Pr ions that are substituted

for Y

in YBa

7−ı

have the effect of “counter-

doping” the CuO

planes with holes and electrons,

respectively.Assuming that each substituted Ca

ion

generates one hole in the CuO

planes,analysis of the

(x, y) data in terms of a phenomenological model

described below indicates that each substituted Pr

ion localizes approximately one hole in the CuO

planes [597] (see below). The localization of holes

is also reﬂected in the behavior of T

as a function of

Pr concentration x in theY

1−x

7−ı

system

(y = 0) Here, T

decreases with increasing x as the

1−x

7−ı

system becomes more under-

doped and vanishes near the onset of the metal-

insulator transition at x

≈ 0.55. The T − x phase

diagram for the Y

1−x

7−ı

system is dis-

played in Fig. 13.91(b) which shows the behavior of

(x)aswellastheN´eel temperatures T

(x)forAFM

ordering of Cu and Pr magnetic moments [282,596].

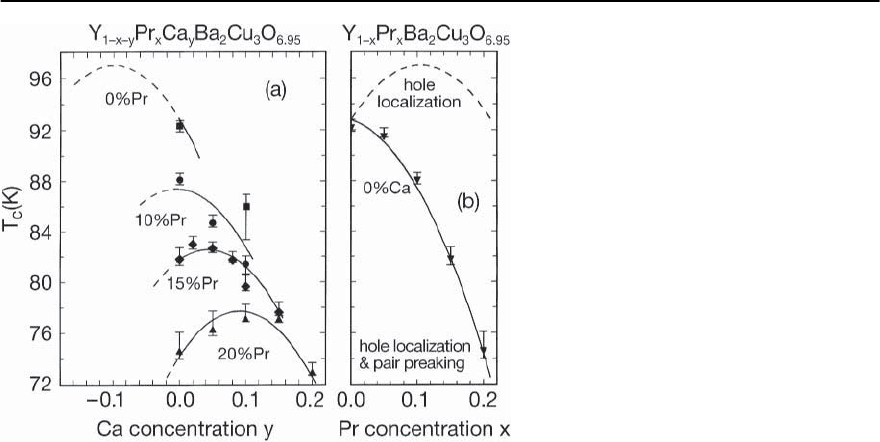
13 Unconventional Superconductivity in Novel Materials 727

Fig. 13.92. (a) Superconducting critical temper-

ature T

vs Ca concentration y forfourPrcon-

centrations x in the Y

1−x−y

7−ı

system [597]. Curves formed by solid and

dashed lines represent Eq. (13.28), as explained

in the text. (b) T

vs Pr concentration x.The

dashed line represents the function T

(x, y =

0) + (96.5K)x,whichdescribespureholelocal-

ization, and the solid line represents the func-

tion T

(x, y = 0), which includes hole localiza-

tion and pair-breaking, after [282,597]

It has been argued that the depression of T

with x

is primarily due to the decrease in the number of

mobile holes with increasing Pr concentration, al-

though magnetic pair breaking by Pr may also be

involved [596,597] (see below). Shown in Fig. 13.92

(a) are plots of T

vs Ca concentration y for four Pr

concentrationsx intheY

1−x−y

7−ı

sys-

tem [597]. Curves formed by solid and dashed lines

represent the equation

(x, y)=T

− A(a − bx + y)

− Bx

= T

(97 K) − (425 K)(0.1−0.95x + y)

−(96.5K)x. (13.28)

The first term is the maximum attainable value of

(97 K),the second term represents the effect of hole

generation by Ca (y) ions and localization of holes

by Pr (x)ions(0.1 is an optimal hole concentration),

while the last term describes the overall depression of

with x due to pair breaking interactions in the lin-

ear low concentration regime. These data illustrate

the inverted parabolic dependence of T

on charge

carrier concentration observed in many supercon-

ducting cuprate systems. Displayed in Fig. 13.92(b)

is a plot of T

vs Pr concentration x.Thedashedline

represents the function T

(x, y = 0)+(96.5K)x which

corresponds to purehole localization,whilethe solid

line corresponds to the function T

(x, y =0)which

includes hole localization and pair breaking.

The occurrence of appreciable hybridization be-

tween the Pr localized 4f electron states and the

valence band states associated with the conducting

CuO

planes was first proposed by Neumeier, Maple,

andTorikachvili in 1988[598]to accountfortherapid

reductionof T

and the striking crossoverin thepres-

sure dependence of T

from positive tonegative with

increasing x in the Y

1−x

7−ı

system. This

proposal was based on similar behavior exhibited by

the La

1−x

system described in Sect. 13.2, in which

therateofdepressionofT

by the Ce impurities dis-

played a strong dependence on pressure that was at-

tributed to the hybridization between the Ce local-

ized 4f states and conduction electron states [56].Di-

rect evidence for Pr localized 4f -CuO

valence band

hybridization was obtained from resonant photoe-

mission spectroscopy experiments (RESPES) on the

1−x

7−ı

system by Kang et al. [599].

Measurements of the pressure dependence of T

were repeated by Maple,Paulius,andNeumeier [600]

on higher quality Y

1−x

7−ı

specimens

studied at zero pressure by Neumeier and Maple

[596].The results of these experiments are shown in

Fig. 13.93 (a) where T

= T

(P)−T

(0) is plotted vs

P for several values of x between 0 and 0.5 [600].The

728 M.B. Maple et al.

T

(P) data are in qualitative agreement with the ear-

lier results and reveal a dramatic crossover from pos-

itive to large negative dependences of T

on P as the

Pr concentration is increased. Earlier measurements

of (T, P)onasamplewithx = 0.5 [596,601]showed

that this sample near the metal-insulator transition

becomes less metallic under pressure.

An extension of the formula for T

(x) for the

1−x

7−ı

system to incorporate the effect

of applied pressure can also account semiquantita-

tively for the remarkable variations in T

with P that

have been observed in the Y

1−x

7−ı

sys-

tem. The trends in the T

(x, P)datacanbeobtained

by assuming that the parameters A and a are, to first

approximation,independent of P,andthatT

, b and

B can be expanded in a power series to first order

in P; i.e.,

(P) ≈ T

(0) + T



(0)P (13.29)

b(P) ≈ b(0) + b



(0)P (13.30)

B(P) ≈ B(0) + B



(0)P (13.31)

The best overall fit of the resultant expression for

[dT

(x, P)/dP]

P =0

to the experimentaldata yieldsthe

values T



(0) = 0.048 K/kbar, b



(0) = 0.0041 K/kbar

and B



(0) = −0.02 K/kbar [600]. The increase of b

with P is consistent with an increase of the valence

(decrease in the 4f electron shell occupation num-

ber) of Pr with P, which is intuitively reasonable. A

decrease (increase) of the magnitude of the exchange

interactionparameter J with P can be inferredfrom

thedecreaseofB



(0) withP,depending upon whether

the complications associated with the Kondo effect

are excluded (included). As discussed in Sect. 13.2,

the Kondo effect is expected (and possibly observed

in the specific heat [602]) in metals containing R ions

that carry magnetic moments when there is strong

hybridizationbetween the localized 4f states of the R

ion and conduction electron states which generates

a large, negative (antiferromagnetic) exchange inter-

action [6]. However, inclusion of the Kondo effect

in the analysis of the T

(x, P) data is complicated.

The calculated T

(x, P) curves for x values corre-

sponding to the experimental T

(x, P) data pre-

sented in Fig. 13.93(a) are shown in Fig.13.93(b)and

give a semiquantitative description of the T

(x, P)

data over the range 0 ≤ x ≤ 0.5, even though

the T

(x, P = 0) data are only described well for

0 ≤ x ≤ 0.2 (see Fig. 13.92(b)).

It is interesting that superconductivitywithvalues

of T

exceeding ∼40 K has only been observed in lay-

ered cuprateswhich havestrongly anisotropic,nearly

two-dimensional electronic properties. An impor-

tant issue for these materials is the nature of inter-

layer transport and the role it plays in the super-

conductivity. Reﬂectance R(!)measurementswith

polarized light reveal that R(!) for the electric field

E parallel to the CuO

planes, E  CuO

, exhibits

a metallic response, while R(!) for E ⊥ CuO

re-

sembles that of ionic insulators with characteristic

phonon peaks in the far infrared. This is illustrated

in Fig. 13.94 where R vs ! data for Tl

CuO

6+x

(Tl2201) [603] are displayed. For temperatures be-

low T

, a sharp plasma edge at ! =37cm

−1

evolves

out of a nearly “insulating” normal state spectrum

since the supercurrents ﬂow in all crystallographic

directions.Inan effortto explore the relationshipbe-

tween changes in the incoherent c-axis conductivity

below T

and the c-axis superﬂuid density, Basov et

al. [603] have analyzed the interlayer conductivity of

the cuprate high T

superconductors Tl

CuO

6+x

2−x

CuO

, and YBa

6.6

,allofwhichshow

incoherent interlayer response in the normal state.

The analysis reveals that the magnitude of the su-

perﬂuid density 

significantly exceeds the weight

missing from the real part of the conductivity in the

frequency region comparable to the superconduct-

ing energy gap 2. This indicates that a significant

fraction of 

is derived from mid infrared frequen-

cies. Basov et al. [603] suggest that the discrepancy

between the magnitude of 

and the spectral weight

that is missing from the far infrared part of the con-

ductivity can be interpreted in terms of an interlayer

kinetic energy change associated with the supercon-

ductivity.

Because of their high values of T

, short coher-

ence lengths, long penetration depths, and large

anisotropy, the cuprate superconductors exhibit a

wealth of striking vortex phases and phenomena that

are currently being vigorously investigated (for a re-

view, see, for example, [604–608]).

13 Unconventional Superconductivity in Novel Materials 729

Fig. 13.93. Shift in T

relative to its value at zero

pressure, T

(P)−T

(0), of Y

1−x

7−ı

samples with various Pr concentrations 0 ≤

x ≤ 0.5 vs pressure P to 18 kbar. (a) Experi-

mental data. (b) Calculated behavior according

to the phenomenological model described in

the text, after [600]

Fig. 13.94. Reﬂectance of Tl

CuO

6+x

mea-

sured with E  c and E  ab polarizations

of incident radiation. The c-axis reﬂectance is

nearly insulating in the normal state but at

T < T

≈ 80 K is dominated by the Josephson-

like plasma edge,after [603]

Symmetry of the Superconducting Order Parameter

A great deal of effort has been expended to de-

termine the symmetry of the superconducting or-

der parameter of the high T

cuprate superconduc-

tors [12, 609, 610]. The pairing symmetry provides

clues to the identity of the superconducting pairing

mechanism which is essential for the development of

the theory of high temperature superconductivity in

the cuprates.

Shortly after the discovery of high T

supercon-

ductivity in the cuprates, it was established from ﬂux

quantization, Andreev reﬂection, Josephson effect,

and nuclear magnetic resonance (NMR) Knight-shift

measurements that the superconductivity involves

electrons that are paired in singlet spin states [611].

Possible orbital pairing states include s-wave, ex-

tended s-wave, and d-wave states. In the s-wave state,

the energy gap (k) is isotropic; i.e., (k)iscon-

stant over the Fermi surface.This leads to“activated”

730 M.B. Maple et al.

Fig. 13.95. Fermi surface gap functions and densities of states of a superconductor with tetragonal symmetry for various

pairing symmetries. The gap functions in the k

=0plane(top) are represented by the light solid lines;distancefrom

the Fermi surface (dark solid lines) gives the amplitude, a positive value being outside the Fermi surface, a negative value

inside. The corresponding density of states for one-quasi-particle excitations N(E) is shown below each gap function,

with N

the normal state value. Gap node surfaces are represented by the dashed lines. Left: The classic s-wave case,

where the gap function is constant, with value . This gives rise to a square-root singularity in N(E)atenergyE = .

Middle: The extended s-wave case derives from pairs situated on nearest-neighbor square lattice sites in real space, with

an approximate k-space form of cos(k

a)−cos(k

a). For the Fermi surface shown here, the gap function has lines of

nodes running out of the page. Right:Ad-wave function of x

− y

symmetry.The extended s-wave and d-wave functions

shownhereeachhavealineardensityofstatesuptoorder, which measures the maximum gap amplitude about the

Fermi surface, after [12]

behavior of the physical properties in the supercon-

ducting state for T  ; e.g., the specific heat C

(T),

ultrasonic attenuation coefficient ˛

(T), and NMR

spin lattice relaxation rate 1/T

(T)varyase

−/T

.For

the extended s-wave state, the energy gap (T)is

anisotropic; i.e., (k) exhibits a variation over the

Fermi surface that has the same symmetry as the

rotational symmetry of the crystal. Similarly, for the

d-wave case,the energy gap (k) is anisotropic; how-

ever, the symmetry is lower than the symmetry of

the crystal. The d-wave state that is consistent with

most, but not all, of the experiments discussed be-

low has d

−y

symmetry, which can be expressed as

(k)=

[cos(k

a)−cos(k

a)]. For both the ex-

tended s-wave and d-wave cases, (k)vanishesat

lines on the Fermi surface, resulting in a density of

states N(E)thatislinearinenergyE at low values

of E. This leads to “power-law” T

(n = integer) be-

havior of the physical properties for T  ; e.g.,

(T) ∼ T

, the superconducting penetration depth

(T) ∼ T,and1/T

(T) ∼ T

. The definitive de-

termination of the symmetry of the superconduct-

ing order parameter requires the determination of

both the magnitude and the phase of (k). Shown in

Fig. 13.95 is a schematic diagram of the variation of

the energy gap over the Fermi surface and the den-

sity of states N(E)vsE for the “s”,“extended s”, and

“d

−y

”states [12].

Magnitude of the Superconducting Order Parameter

A number of different types of measurements have

been performed on the high T

cuprate supercon-

ductors that are sensitive to |(k)|. These include

microwave penetration depth (T) [612],microwave

surface conductivity [613], nuclear magnetic reso-

nance (NMR) relaxation rate 1/T

(T) [614], mag-

netic field dependence of the electronic specific heat

(T) [615], thermal conductivity [616], angle re-

solved photoemission spectroscopy (ARPES) [617],

quasiparticle tunneling [618,619] and Raman scat-

tering [620]. The results of these studies are gen-